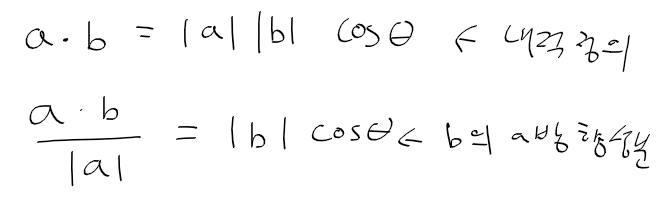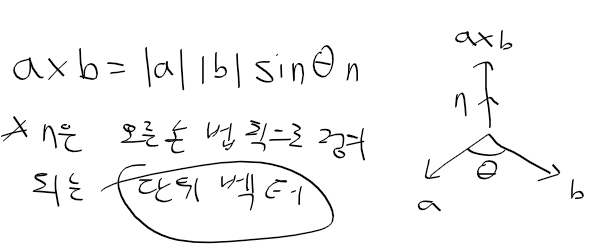집밖은 위험해

예전부터 공업수학을 공부해야지 생각은 하고 있었지만

가장 유명한 크레이직 공업수학인가?

그런 책들을 보면 

무수한 예제와 증명을 보고 겁에 질려 포기하고 말았었다.

공업 수학을 왜 공부해야하는지에 대한 고민 없이 하다보니 더 그랬던것 같았는데

결국 돌아돌아

최적화 이론, 수치해석 같은 학문을 배우기 위해서

공업수학을 공부하게 되었다.

이번에 공업수학을 배우기 전에는 공업 수학이라는 학문이 무엇을 하는지는 잘 몰랐었다.

나보고 봐야 된다고 말하는 사람도 잘 없었고,

그나마 한번 봤을때 전체적인 틀을 보고 시작하는게 아니라

처음부터 세부적으로 보는데, 수많은 공식과 증명 과정들만 보고 포기해버리고 말았는데,

그나마 그래프 기반 슬램에서 최적화 관련 개념들을 보고 수치해석을 공부 하려고 시작하다가

수치 해석의 개요에서 공업수학이 미분 방정식을 다루는 학문이다 정도로 나마 막연하게 알게되어

수치해석을 시작하기 전에 본격적으로 살펴보게 되었다.

그 동안 공부하면서 삽질과 이론 공부 흐름을 고민하면서

내가 필요한 부분들 넘어가도 되는 부분들을 생각하면서

공업수학을 공부하다보니 생각보다 빠르게 둘러 볼 수 있었다.

예전에 신호와 시스템, 제어 공학을 배울때는

왜 물리적인 현상을 미분 방정식으로 모델링하는지 잘 몰랐었다.

당시 눈앞에 보이는 푸리에 변환, 라플라스 변환 공식과 이동 성질,

예제 푸는데만 혈안이 되있다 보니

많은 시간을 들인 덕에 그러한 예제들은 풀수 있을지는 몰라도

제어 공학과 신호와 시스템에서 왜 미분방정식이 사용되는지, 시스템이 무엇인지와 같은

개념들을 쌓는데는 등한시 하고 말았었다.

그렇게 삽질하면서 공부한 문제 푸는 방법도 다 잊어버렸으니

남은게 아주 많지는 않더라

하지만 그런 삽질 덕분에

이번 공업 수학에서 수학적 모델링과 해를 구하는 과정에 대해

문제 풀이보다 개괄적인 이론에 대해 살펴볼수 있었던것 같다.

그렇게 다양한 학문에서 다루는 문제를 수학적 모델링을 하고, 방정식을 만들어 해를 구하는 과정에 대한 개념과

그러한 수학적 모델링을 위한 1차, 다차 미분 방정식, 시스템과 다양한 해를 구하는 방법

그리고 행렬과 벡터 이론을 통한 벡터 미적분 일부 까지

조금 더 깊이 들어간다면 더 들어갈 수 있지만 이 정도 보기 만해도

내가 공부하는 응용분야에서는 충분할것 같다.

특히 다양한 문제들을 수학적으로 모델링하고

이 모델링한 방정식의 특성에 따라 해를 구하는 등

해석적, 수치적 방법론에 대한 전반적인 배경지식을 조금 더 확립할수 있어서 잘봤다.

다음에는 베이즈 통계학, 수치해석, 최적화 이론 중 아무거나 공부해보고자 한다.

자연 과학에서 유용하게 사용되는 도함수

- 기울기 벡터, 발산, 회전

기울기 벡터 gradient

- 스칼라 함수 f가 주어질때 grad f가 기울기 벡터

방향 도함수 directional derivative

- 스칼라 함수 f의 a 방향 변화율

- D_a f는 a 방향의 변화율로 theta 값에 따라 i방향과 j방향 성분을 구할수 있음.

 -> 방향도 함수는 편미분을 임의의 방향으로 나타낸 개념

기울기 벡터의 의미

- 스칼라 함수 f의 기울기 벡터는 다음의 방향을 가리킨다.

포텐셜 potential과 보존장 conservative field

- 아래의 식이 주어질때 스칼라 함수를 기울기 벡터의 포텐셜, 기울기 벡터를 보존장

등위 곡선과 법선 벡터

- 곡선 f(x, y) = c가 곡면 z = (x, y)의 등위 곡선일때, 곡면의 매개변수 벡터함수 r(t) = [x(t), y(t)]로 정의

- 곡선 f(x, y) =c 를 시간 t에 대해서 미분하면 다음과 같다.

=> 법선 벡터는 스칼라 함수 f가 가장 급격히 증가하는 기울기 벡터

스칼라 함수 scalar function

- 함수의 크기만을 구하는 함수

벡터 함수 vector function

- 크기와 방향을 동시에 가지는 함수

- 스칼라 값들을 요소로 가짐

벡터장 vector filed

- 벡터 함수의 크기와 방향을 함께 그린 그래프

ex. 속도장 velocity field, 힘장 force filed, 자기장 magnetic field

다변수 함수 개요

- 대부분의 현상과 공학 문제는 다변수 함수로 표현됨

1변수 함수 single variable funtion

- y = f(x)와 같이 하나의 독립 변수만을 가지는 함수

도함수(미분)

- 1변수 함수에서 함수 y의 x에 대한 변화율

다변수 함수 mutiple variable function

- f(x, y) = z와 같이 독립 변수가 2개 이상인 함수

등위 곡선 level curve

- 2변수 함수에 z = c 로 얻을수 있는 곡면

상미분 ordinary derivative

- 1변수 함수 y = f(x)의 도함수(미분)

편미분 partial derivative

- 다변수 함수에서 종속변수의 한개의 독립변수에 대한 변화율

계급 rank

- 행렬 A가 주어질때, 1차 독립인 행 벡터의 최대 갯수를 계급이라 부름. rank A로 표기

* 행 벡터가 3개가 있더라도 1차 독립인 행 벡터가 2개 뿐이면 계급은 2가 됨.

동차 선형 시스템 homogeneous linear system

- 입력 벡터 B가 0인 선형 시스템으로 자명해 trivial solution은 모두 0이 됨.

역행렬 inverse matrix

- 정사각 행렬 A, B가 주어질때 A B = I를 만족하는 행렬 B는 A의 역행렬

역행렬의 존재 여부에 따른 분류

- 정착 행렬 regular matrix, 가역행렬 invertible matrix : 역행렬이 존재하는 행렬

- 특이 행렬 singular maxtrix : 역행렬이 존재하지 않는 행렬

행렬식 determinant

- 행렬의 판별식

- 2 x 2 행렬식

- 3 x 3 행렬식

부분행렬 submatrix

- 성분 a_ij의 행과 열을 제외한 행렬

여인수 cofactor

-해당 행렬의 성분에 대한 부분 행렬의 행렬식

수반 행렬 adjoint matrix

- 행렬 A의 역행렬을 구할때 사용되는 행렬

수반 행렬로 역행렬 구하기

크래머의 공식 cramer's formula

- 선형 시스템 AX = B가 주어질떄 k번쨰 성분의 해를 구하는 법

가우스 소거법 gauss elimination method

- 선형 시스템의 해를 구하는 방법 중 하나

- 행이나 열을 서로 교환하거나 기본 행연산을 쉽게 정리하도록 선형 시스템 AX = B에서 행렬 A와 열 벡터 B결합하여 아래의 첨가 행렬 augmented matrix을 만듬 

- 첨가 행렬을 사다리형 행렬 echelon form로 변환 후 아래에서 위로 역대입 backward subsitution하여 미지수를 구함

사다리형 echelon form만들기

1. 행렬 A의 a_11을 기준으로 a_i1(2 <= i <= n)을 0으로 만듦

2. a_22를 기준으로 a_i2(3<=i<=n)을 0으로 만듦

3. 위 과정을 반복하여 행렬 A의 주대각성분 아래 모든 요소들을 0으로 만듬

- 다음 행의 성분들을 0으로 만들기 위해 각 행들은 다음 연산을 수행(예제 보면서 이해 필요)

4. 사다리형 결과

역대입 backward subsitution

- 사다리형의 마지막 행인 n행에서 x_n을 구하고

- 이를 순차적으로 역대입하여 나머지 미지수를 구할 수있음

가우스 소거법을 이용현 선형 시스템의 해를 구하기

1. 선형 시스템 행렬로 정리하기

- 다음의 선형 시스템이 주어질 때

- 행렬로 정리하면 아래와 같다

2. 사다리꼴 만들기

- 이를 사다리꼴 형태로 정리하기 위해 첨가 행렬을 구하면 다음과 같다.

- 2번째, 3번쨰 행의 첫번째 요소를 0으로 만들기 위해, a_11을 기준으로 m_ki를 구하면

- 다음의 연산을 수행하면 2, 3번쨰 행의 첫번쨰 요소들이 0이 된다.

- 3번째 행의 2번째 요소도 0으로 만들어주어야 하므로 m_32를 구하고 연산을 수행하자

3. 역대입 수행하기

- 역대입을 통해 마지막 행 x_3을 다음과 같이 구할수 있음

4. 선형 시스템의 해 정리

- 선형 시스템에서 가우스 소거법으로 구한 해는 다음과 같다.

가우스 조던 소거법

- 가우스 소거법에서 계수 행렬 A를 위삼각 행렬로 만들고, 임의의수 한개만 존재하는 마지막 행에서 역대입으로 모든 해를 구함

- 첨가 행렬을 대각 또는 단위 행렬로 만들면, 각 행이 한개의 임의의 수만 가짐 -> 역대입 불필요

=> 가우스-조던 소거법

* 계수 행렬 A를 단위 또는 대각 행렬로 만드는데 연산이 더 많이 필요함

행렬식 determinant

- 정사각행렬 A에 대한 식으로 행렬에 대한 판별식

- 아래와 같이 표기

행렬식과 다양한 행렬들

- 행렬 A가 주어질때

- 특이행렬 singular matrix : detA = 0일때, A는 특이 행렬

- 일반 행렬 regular matrix : detA != 0 일때, A는 일반 행렬

행렬식 계산 방법

1. 여인수법

2. 삼각형법

이 있으나 생략

선형 시스템의 중요성

- 많은 자연, 공학 분야의 문제가 선형 시스템으 표현함

 -> 선형 시스템의 해를 구하는것이 매우 종요함.

- 현상을 미분 방정식으로 나타내도 해석적으로 해를 못구하는 경우 수치적으로 구해야 함.

차분 방정식 difference equation

- 수치적으로 구하는 경우 미분 방정식을 작게 나눈 구간으로 얻는 차분 방정식을 품

- 차분 방정식은 대규모 선형 시스템으로 이루어 짐

선형 시스템의 해를 구하는 방법

1. 직접 법 direct method

- 가우스 소거법, 역행렬, 크래머 공식

2. 반복법 iterative method

- 수치적 방법에서 많이 사용

선형 방정식 linear equation

- 상수 a, b, c, d가 주어지고 변수 x, y, z에 대한 아래와 같은 식을 선형 방정식이라 함

- 일반화하여 선형 방정식을 정리하자면 다음과 같다.

선형 시스템 linear system

- 여러개의 선형방정식으로 이루어 진 형태를 선형 시스템(1차 연립방정식)이라고 부름.

- 미지수 n개인 m개의 선형 방정식으로 이루어진 선형 시스템은 아래와 같음.

선형 시스템의 행렬 표현

- 행렬 A : m x n 형태의 계수 행렬 coefficient matrix

- 벡터 X : n x 1의 해 벡터 solution vector

- 벡터 B = m x 1의 입력 벡터 input vector

선형 시스템의 관련 용어

- 동차 선형 시스템 homogeneous linear system : 입력 벡터 B의 성분들이 모두 0인 경우의 선형 시스템

- 비동차 선형 시스템 nonhomogeneous linear system : 동차 선형 시스템이 아닌 선형 시스템

- 과잉결정 over determined : 식의 개수 m이 계수의 갯수 n보다 많은 경우

- 결정 determined : 식과 계수의 갯수가 같은 경우

- 과소 결정 under determined : 식이 계수보다 수가 적은 경우

- 일치 consistent : 해를 적어도 한개라도가지는 경우

- 불일치 inconsistent : 해가 전혀 없는 경우

행렬

- 숫자를 직사각형 형태로 나열

- 선형계 해석, 고유값 문제, 최적화, 컴퓨터 그래픽 등 다양한 분야에서 응용

미분 방정식 경계값 문제에서의 행렬

- 수치적으로 풀면 결과가 행렬로 연립방정식의 해를 구하는 문제가 됨

행렬 matrix

- 직사각형 형태의 숫자들의 배열

정사각행렬 square matrix

- 행과 열의 길이가 같은 행렬

- 주대각성분 principal diagonal component : 정사각행렬의 대각선 위의 성분

영행렬

- 행렬의 모든 성분이 0인 행렬

사상 mapping 및 변환 transformation

- 벡터 공간 X, Y에서 X에속하는 벡터 x가 Y에 속하는 벡터 y에 대해 y = F(x)로 대응 correspondence하는 것

1차 변환 linear transform

- 선형성을 만족하는 변환

확률 행렬 stochastic matrix

- 모든 성분이 음의 값이 아니고, 각 행 요소들의 합이 1인 정사각행렬

마르코브 과정 markov process

- 현재 상태에 대한 확률이 이전 상태에 의존하는 확률 과정

전치 행렬 transpose matrix

- 행과 열을 바꾸어 얻는 행렬

삼각행렬 triangular matrix

대각행렬 diagonal matrix

- 주대각 성분을 제외하고 나머지 요소들이 0인 행렬

스칼라 행렬 scalar matrix

- 주대각성분이 모두 같은 대각 행렬

단위 행렬 unit matrix

- 주대각성분이 1인 스칼라행렬

벡터 공간의 개요

- 벡터를 2차원, 3차원에서 제한할 것이 아니라 n차원 까지 확장하여 다룰수 있음

- 이런 확장된 차원의 벡터를 벡터 공간 집합의 원소로서 다룸

벡터 공간 vector space

- 집합 V가 덧셈과 스칼라곱이 정의되는 원소 집합일때, 10가지 공리를 만족하는 집합 V를 벡터 공간

- 벡터 공간 V의 원소를 벡터

* 자세한 공리는 생략

- 스칼라를 실수로 제한하면 -> 실 벡터 공간 real vector space

- 복소수 까지 다룬다면 -> 복소 벡터 공간 complex vector space

벡터 공간의 예시

1. 실수 집합 R

2. n차원 실벡터의 집합 R^n

3. n차 이하 다항식 집합 P_n

4. 모든 실수에 정의되는 실 함수 f 집합

등

부분 공간 subspace

- 벡터 공간 V의 부분집합 W가 V에서 정의되는 덧셈과 스칼라곱을 따르는경우

 => 부분집합 W는 벡터 공간 V의 부분 공간

1차 결합 linear combination

- 아래와 같이 스칼라에 대해 벡터가 주어지면 1차 결합

1차 독립 linear independent 및 1차 종속 linear dependent

- 아래의 벡터와 스칼라의 1차 결합이 c1 = c2 = ... = c0에서만 성립되면 벡터들은 1차 독립

- 아닌 경우에 성립되면 1차 종속

기저 basis

- 벡터 공간 V의 모든 벡터가 1차 독립인 벡터 x1, x2, ..., xn의 1차 결합으로 표현가능한 경우

 -> x1, ... , xn을 벡터 공간 V의 기저

차원 dimension

- 기저를 이루는 벡터의 갯수를 벡터공간 V의 차원 -> dimV 로 표기

생성공간 span

- 주어진 벡터의 모든 1차 결합 집합

벡터의 곱

- 내적 inner proudct와 외적 outer product

내적이란?

- 두 벡터의 곱으로 차원이 하나 감소하여 내적이라 부름.

- 점 연산이라 dot product 혹은 결과가 스칼라 값이라 scalar product라고도 부름

사영벡터란?

- 두 벡터 a와 b가 주어질때, b를 a의 벡터 선상에 사영하여 얻는 a방향의 벡터

 => a에 대한 b의 사영벡터 projection vector of b onto a

- 내적의 정의에 따라 b의 a방향 성분을 구하면

- 사영 벡터의 크기

- 단위 벡터를 이용한 사영 벡터 표현

외적 outer product

- 외적에 의해 하나의 차원이 증가하여 외적이라고 부름.

- 두 벡터 a, b의 외적을 a x b로 표기하므로 cross product

- 혹은 외적의 결과가 벡터이기 때문에 vector product

외적 계산

-  다음과 같이 벡터 성분이 주어질때 외적 계산