예측방법론
- 예측에는 주관적 예측과 객관적 예측이 있음
- 데이터 기반 예측 -> 객관적 예측
- 시계열 특성과 예측 모형을 보고 R 구현
회귀 분석 regression analysis
- 독립변수와 종속변수 사이의 함수 관계(모형)을 구하는 통계적 분석 방법
- 독립 변수 independent variable, 설명변수 explanatory variable: 영향을 주는 변수 x
- 종속변수 dependent variable, 반응변수 response variable : 영향을 받는 변수 y
회귀 용어의 유래
- 영국의 우생할자 galton이, 부모콩의 무게를 x 자식콩이 무게를 y로 산점도를 그려 관계를 살펴봄
=> 자식의 무게는 평균 무게로 회귀(되돌아 가려는)하려는 경향을 발견 => 피어슨이 분석하여 발표
단순 회귀 모형 simple regression model
- 가장 간단한 회귀 모형
- 독립 변수와 종속 변수 사이에 선형적 관계를 표현함

- Yi : i번째 측정된 반응변수 Y의 값
- beta 0 : 절편 회귀계수
- beta 1 : 기울기 회귀계수
- Xi = i번쨰 상수 X값
- epsilon i = i번쨰 측정된 Y의 오차항
회귀선 regression line
- 표본으로 모형식을 추정하여 구한 직선. 추정된 회귀 직선, 회귀선이라 함.
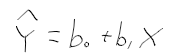
-b0와 b1은 beta0와 beta1의 추정값
- hat{Y}는 E(Y)의 추정값
- b0는 회귀절편 intercept
- b1은 X가 한단계 증가할떄 hat Y의 증가량으로 기울기 slope
- 회귀 계수 b0, b1을 구하는 방법 => 최소제곱법
최소제곱법 method of least square LSM
- 회귀 모델이 다음과 같이 주어질떄

- 오차 항 제곱 합은 아래와 같다.
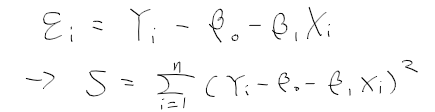
- > S를 beta0과 beta1에 대해 각각 편미분한 결과가 0이 되는 beta0와 beta1를 b0와 b1로 함.

-위 식을 정리하면 아래와 같으며, 이 식을 정규 방정식 normal equation
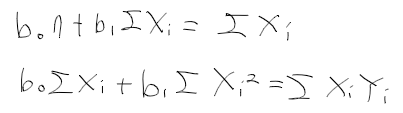
- b0와 b1에 대하여 정리

선형 회귀 모델 예제 - 광고료와 총판매액
- 기울기는 2.6087으로 추정 p value가 매우 작으므로, 귀무가설 기각 -> 유의한 결과를 보임
- 절편은 -2.2696으로 추정

잔차 residual
- Xi에서 관측된 값 Yi와 추정된 hat Yi사이 차이

- 잔차의 합은 0
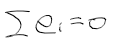
- 잔차의 제곱합은 최소
- 관찰값 Yi의 합과 추정된 hat Yi는 같다.
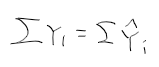
- R에서 확인하기

회귀 모형의 정도
- 구한 회귀 모형이 얼마나 좋은가?
분산 분석표에 의한 F 검정
- 변동 분해하기
회귀제곱합의 자유도는 독립변수가 1개이므로
총 데이터 수가 n개에서 평균에 대한것을 빼므로 n - 1
=> 잔차제곱합의 자유도는 n - 2
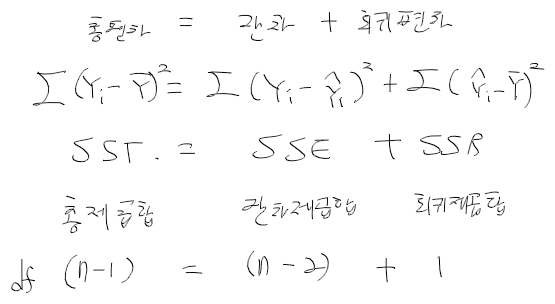
분산분석표를 이용한 F 검정
- 변동을 분해한 표
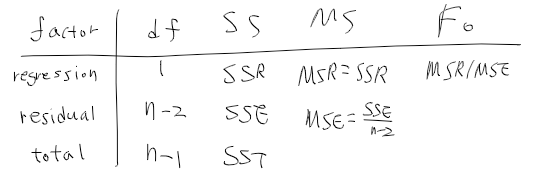
- 가설 검정

- F0 > F(1, n-2; alpha) 이면 유의수준 alpha에서 귀무가설을 기각 => 회귀 직선이 유의하다
- R에서 유의 확률 p value를 제공. pvalue < alpha이면 귀무가설 기각
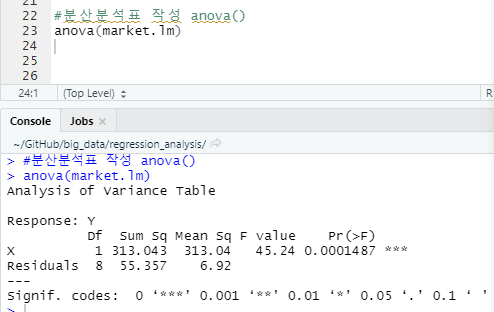
R에서 분산분석
- p value가 0.001487로 매우 작으므로 귀무가설을 기각
결정계수 coefficient of determination
- 회귀선이 어느정도의 설명력을 가지고 있는가를 나타내는 지표
- R^2는 0 ~ 1
- X와 Y 사이 높은 상관관계를 가질수록 R^2 는 1에 가까워짐
-> 0에 가까우면 유용성이 떨어지는 회귀선
- 회귀선으로 설명되는 변동/총변동이므로 회귀선의 기여율이라고도함.

추정값의 표준 오차 Mean Squared Error
- 잔차 평균 제곱 MSE는 오차 분산 sigma2의 불편추정량.
- sqrt(MSE)로 표준 오차를 구함

'수학 > 통계' 카테고리의 다른 글
| 회귀모형 - 3. 회귀 모형에서 변수 선택 (0) | 2020.10.30 |
|---|---|
| 회귀모형 - 2. (다)중회귀모형 (0) | 2020.10.30 |
| 실험계획 - 5. 회귀분석과 공분산 분석 (0) | 2020.10.29 |
| 실험계획 - 4. 이원배치 분산분석 (0) | 2020.10.29 |
| 실험계획 - 3. 일원배치 분산분석 (0) | 2020.10.29 |