변수 선택과 기준/방법, 다중 공선성
다중 회귀 모형
- 여러개의 독립변수에 의해 종속변수 y에 주는 영향을 함수 식으로 표현한것
변수선택 variable selection problem
- 많은 설명 변수 중에서 모형에 포함시킬 변수를 결정하는 것
다중공선성 multicollinearity
- 모형에 포함되는 설명변수들 사이 연관성이 존재하는 경우 모형의 안정성과 신뢰성을 떨어트림
=> 공선성, 다중공선성
- 두 설명변수 X1, X2가 상수 c0, c1,c2에 대해 다음 관계를 가지는 경우
-> 두 변수 사이에 완벽한 공선성(exact collinearity)가 있음

ex. X1 + X2 = 100인경우 X2는 X1으로 결정됨
다중공선성 multiconllinearity
- 설명변수가 2개가 넘는 경우 다음과 같은 관계가 성립하거나 근사적으로 성립할시
=> 설명변수들 사이에 다중 공선성 multiconllinearity이 존재

- 설명변수 Xh와 나머지 설명변수간의 결정계수(다중상관계수의제곱) Rh^2이 다중공선성의 정도를 나타냄.
다중 공선성에 대해 의심이 드는 경우
- 설명변수의 표본 상관행렬에서 상관계수가 크게 +-1에 가까울떄
- 설명변수를 모형에 추가/제거시 추정된 회귀계수의 크기나 부호에 큰 변화를 줄때
- 새 자료를 추가/제거시 추정된 회귀 계수의 크기나 부호에 큰 변화를 줄때
- 중요하다고 생각되는 설명변수의 검정 결과가 유의하지 않거나 신뢰구간이 넓을때
- 추정된 회귀 계수의 부호가 과거의 경험이나 이론적인 면에서 기대되는 부호와 상반될때
분산팽창인자 VIF; variance inflaction factor
- R_j^2 : Xj를 반응변수로 보고 나머지 설명변수에 대한 결정 계수
- k개의 VIF_j 중 가장 큰 값이 5~10이 넘으면 다중공선성 있다고 판단.

병원 데이터를 이용한 예제
1. 데이터
Y : 월간 의사 연 근무시간
X1 : 일평균 환자수
X2 : 월간 Xray 초라영 횟수
X3 : 월간 이용병석수
X4 : 해당지역 병원이용가능인구 / 1000
X5 : 평균입원일

2. 회귀모형 구하고 보기
- X1 일평균환자 : 늘어날수록, 근무시간 Y는 늘어날탠대 -15.85167이 나옴
- X4 병원가능인구가 늘어날수록, 근무시간 Y는 늘어나야하나 -4.219가 나옴.
- X5 평균입원일이 늘어날수록, 근무시가이 늘어야하나 -394...
=> 독립변수간에 다중공선성이 존재가 예상되며, 분산 팽창인자 등에 의한 진단이 필요.

3. 분산팽창인자 계산하기
- X1, X2, X3, X4의 분산팽창인자를 계산해보면 5이상으로 다중 공선성 문제가 존재

4. 독립변수간 상관관계 보기
- cor()함수 : 상관계수 행렬
- X5를 제외한 X1 ~ X4까지 강한 선형 상관관계가 존재. x5를 제외하고 대부분 1에 가까움.

설명변수 X1을 제외한 경우 모형을 보자
1. summary
- R2는 차이없음
- 추정된 회귀계수의 표준 오차는 조금 줄어듬

2. 분산팽창지수 보기
- x1이 포함되었을때보다 크게 줄어듬

모형 선택 기준 - 결졍 계수
- R_p^2는 k개의 설명변수중에서 p개의 설명변수로 구성되는 모형에서 아래처럼 정의
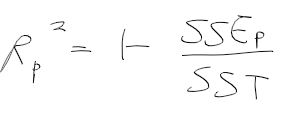
- 결졍 계수는 설명 변수가 추가되어 p가 커질수록 증가
=>모든 변수가 포함이 다된 모형(p=k)일때 최대되도록 증가
= 최대 결정계수 값인 모형을 선택은 의미 없음.
모형 선택의 기준 - 수정 결정계수 adjusted coefficient of determination
- 결정계수 R_p^2의 문제를 보완하기 위한 방법.
- SS를 그대로 쓰기보다 자유도로 나누어 조정과정을 거침
- bar R_p^2는 설명변수가 증가해도 항상증가하지않음
=> 모형 선택시 수정 결정계수가 큰것을 사용하자
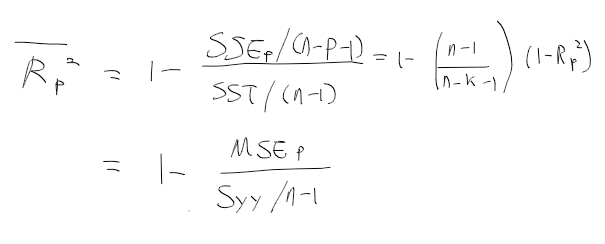
모형 선택 기준 : mallows Cp 통계량, AIC
- k개의 독립변수 중에서 p개의 변수를 선택할때, C_p가 최소가되는 모형을 선택

- AIC : 작은값을 갖는 모형을 선택
변수 선택 방법
- 모든 가능한 회귀 all possible regression
- 앞에서부터 선택 forward selection
- 뒤에서부터 선택 backward elimination
- 단계별 회귀 stepwise regression
1. 모든 가능한 회귀
- 독립변수가 k개 있으면 2^k -1 개의 회귀모형을 다뤄보자
=> k가 커질수록 계산량이 급격히 늘어남
1.1 데이터 로드
- 독립변수 4개,

1.2 모든 가능한 회귀 수행
- leaps 패키지의 regsubsets()함수
- 선택 알고리즘 : exhaustive
- 독립변수가 1개인 경우 가장 좋은 모형은 X4
- 독립변수가 2개인경우 가장 좋은 모형은 X1, X2
- 독립변수가 3개인 경우는 X1, X2, X4

1.4 구체적인 통계량을 보기
- 아래의 통계량을 정리해보면 X1, X2, X4가 사용된경우 조정된 R2가 가장 크고
- X1, X2인 경우 Cp가 가장 작다
- Cp는 작을수록 좋고, 조정된 R2는 클수록 좋다.
=> X1X2 나 X1X2X4 선택

2. 앞에서부터 선택 forward selection method
- k개의 설명변수 중에서 가장 영향이 큰 변수부터 하나씩 선택
- 더이상 중요한 변수가 없다고 판단할때 선택 중단하는 방법
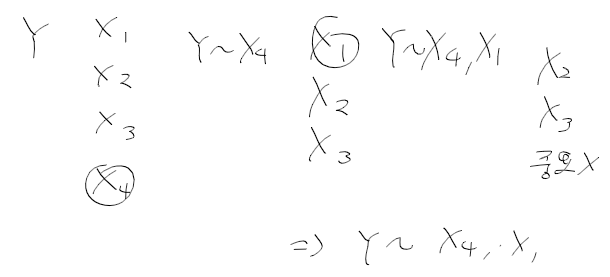
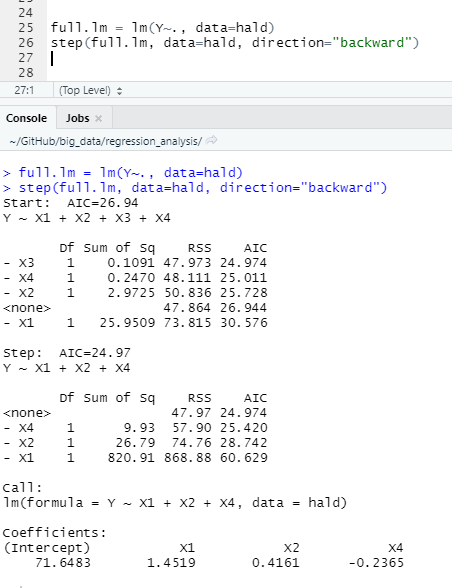
2.1 R에서 실습
- AIC기준으로 수행. AIC는 값이 작을 수록 좋음.
- X3은 없는게 나으므로 X4, X1, X2를 선택

뒤에서부터 제거 backward elimination method
- 모든 독립변수를 사용한 모델에서부터 기여도가 작은 변수를 제거해나가는 방법
단계별 회귀 stepwise selection
- 앞에서 선택법에 뒤에서 제거법을 가미
- 새 변수가 추가될떄마다 기존 변수가 제거 될 필요가 있는지 검토하여 선택
Y~1에서
+X4하는 경우 AIC
~ +X3하는경우 AIC
=> X4를 추가하는것이 AIC가 가장작다
Y~X4에서
+X1하는경우 / +X3하는경우 / 추가 x/ +X2 경우 / -X4 경우
=> +X1일떄 AIC가 가장적다. => X1 추가
...
더하는 경우와 빼는 경우를 동시에 고려

'수학 > 통계' 카테고리의 다른 글
| 회귀모형 - 5. 일반화 선형 모형 (0) | 2020.10.30 |
|---|---|
| 회귀모형 - 4. 회귀 모형 만들기 (0) | 2020.10.30 |
| 회귀모형 - 2. (다)중회귀모형 (0) | 2020.10.30 |
| 회귀모형 - 1. 단순 회귀 모형 (0) | 2020.10.30 |
| 실험계획 - 5. 회귀분석과 공분산 분석 (0) | 2020.10.29 |