이원배치법
- 2개의 요인(독립변수 A, B)와 반응 변수(종속변수) 사이의 관계를 알아보기위한 실험계획
- 독립 변수는 불연속, 종속 변수는 연속적인 값
- 반복이 없는 경우와 있는 경우가 존재
- 반복하는 경우 두 요인간 상호 작용 효과를 검출 가능
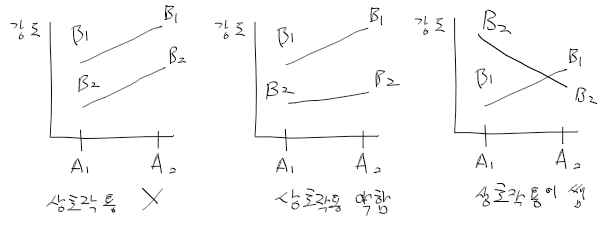
이원배치법에서 효과
- 주 효과 main effect : 요인 A의 수준간 차이가 존재하는가
- 상호 작용 효과 interection effect(교호 작용효과) : 요인 A의 서로 다른 수준에서 요인 B의 주효과가 다른가
실험의 랜덤화
- 완전 확률화 계획법 : 두 요인 수준 조건에 순서를 주고, 랜덤한 순서대로 실험
이원 배치법 고정모형(A, B 고정요인- 모수인자)
- 반복의 장점
인자 조합의 효과를 실험 오차와 분리하여 구할수 있음
교호작용을 분리하여 검출할수 있어 주효과에 대한 검출이 개선됨
실험 오차를 구할 수 있음
- 이원배치법의 자료구조

반복이 있는 이원배치 모수모형 (A, B 두인자 모두 고정, 모수인자인경우)

검정 가설
1. 인자 A에 대한 가설
H0 : alpha1 = alpha2 = ... = 0 ->인자 A의 수준간 효과 차이 없다.
vs H1 : 적어도 하나의 alphai는 != 0 -> 인자 A의 수준관 효과 차이 있다.
2. 인자 B에 대한 가설
H0 : beta1 = beta2 = ... = 0 -> 인자 B의 수준간 효과에 차이가 없다
vs H1 : 적어도 하나의 betai는 != 0 -> 인자 B의 수준간 효과 차이 존재
3. 인자 A와 B의 교호작용에 대한 가설
H0 : 모든 (alpha beta)ij = 0 -> 교호작용 없다
vs H1 : 적어도 (alpha beta)ij 중 하나는 0이 아니다 -> 교호작용이 존재
이원배치 분산 분석

이원배치 분산 분석표

이원배치 분산 분석에서 가설검정
1. 인자 A에 대한 가설검정
- 검통 통계량 F0 = MSA / MSE > F(a -1, ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각
즉, 인자 A가 반응치에 유의한 영향을 준다.
2. 인자 B에 대한 가설검정
- 검통 통계량 F0 = MSB / MSE > F(b -1, ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각
즉, 인자 B가 반응치에 유의한 영향을 준다.
3. 교호작용 AxB에 대한 가설검정
- 검통 통계량 F0 = MSAxB / MSE > F( (a-1)(b-1), ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각
즉, 인자 A와 B 사이에 교호작용이 존재한다.
이원배치 분산분석 예제
- 4종류의 사료와 3종류의 돼지 품종이 체중 증가에 미치는 영향

R에서 예제 실습
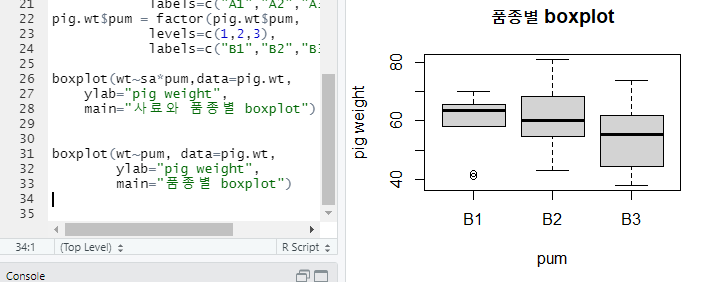
- 사료와 품종별 boxplot

- 품종별 boxplot 상에서
품종간에 큰 차이는 없어보임
사료별 boxplot
- 사료별 큰 무게 분포를 보인다.

분산분석
- 사료에 대한 유의확률 p val 0.00223로 매우 작음. 귀무가설 기각
=> 사료가 몸무게 증가에 유의한 영향을 준다.
- 나머지의 경우 유의확률이 크므로 귀무가설 채택.

'수학 > 통계' 카테고리의 다른 글
| 회귀모형 - 1. 단순 회귀 모형 (0) | 2020.10.30 |
|---|---|
| 실험계획 - 5. 회귀분석과 공분산 분석 (0) | 2020.10.29 |
| 실험계획 - 3. 일원배치 분산분석 (0) | 2020.10.29 |
| 실험계획 - 2. 두 모집단 비교 (0) | 2020.10.29 |
| 실험계획 - 1. 실험 계획 개념 (0) | 2020.10.29 |