기존의 회귀 모형 regression model
- 기본 가정 : 오차 등분산성, 모형의 선형성, 오차의 정규성

반응 변수 Y가 정규 분포가 아닌경우
- 오차의 등분산성 위배 -> 분산안정화변화로 해결
- 오차의 정규성이 위배(오차가 정규분포를 안따를떄) : 일반화 선형 모형
일반화 선형 모형를 사용하는 경우
- 반응변수 Y가 정규분포를 안따르는 경우
ex. 반응변수가 비율을 나타내는 경우, 반응변수가 양의 개수를 나타내는 포아송 분포를 따르는 경우
일반화 선형 모형 generalized linear model
- 반응 분포가 정규 분포 뿐만아니라, 이항분포, 포아송분포,
감마 분포와 같은 지수족 분포를 따를때 회귀 모형 형태로 확장된 모형
* 회귀모형의 한계를 극복함.
일반화 선형 모형의 구성성분 세가지
- 반응 변수의 분포
- 선형 예측자 eta = beta_0 + beta_1 X = g(mu)
- 연결 함수 g(mu) = log(mu)
예시 : 1983 ~ 1986년 동안 호주에서 에이즈로 인한 사망자수
x : 1983년 1월부터 3개월 단위 경과 기간
y : 사망자수
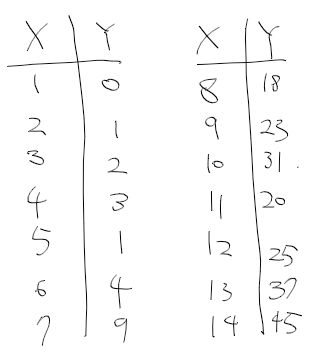
선형 모형의 일반화 선형 모형으로 확장
| 선형 회귀 모형 | 일반화 선형 모형 | |
| 반응변수의분포 | 정규분포를 가정 | 정규분포, 이항분포, 포아송 등 지수족 분포 등 하나를 가정 |
| 평균의 선형성 | mu = E(Y) = X' beta | eta = g(mu) (연결함수) = X' beta |
| 모수 추정법 | 최소제곱추정(=최대가능도추정) | 최대가능도추정 |
지수족 분포 the exponential family of distributon
- 반응변수 분포가 지수족 분포를 따를때 일반화 선형 모형 사용
- 확률 밀도함수 f(y;theta;phi)와 같이 표현되는 분포로 아래와 같음.
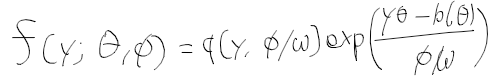
- theta : 평균 mu의 함수로 정준 모수 canonical parameter
- phi : y의 분산과 관련되고, 평균과는 독립인 산포모수 dispersion param
- w : y 분포 가정에 따라 사전에 알수있는값
선형 예측차 eta linear predictor
- 설명변수들의 선형 결합

연결 함수 link function
- 선형 예측자와 반응변수의 평균 사이 관계를 eta가 되도록 만들어주는 함수 g()
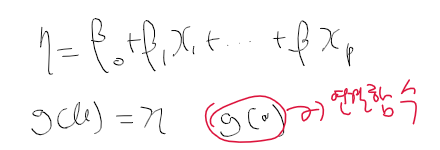
지수족 분포의 정준 연결 canonical link

로지스틱 회귀모형
- 반응 변수가 이항 자료인 경우 사용
=> 로지스틱 회귀모형 : 로짓 함수가 선형 연측자가 되는 모형.
ex. 날다람쥐의 출현 자료( 독립 : con_metric , p_size_km, 종속: 1 또는 0)
=> y = occur, 1=yes, 0= no => 이항분포를 따름

- 로지스틱 회귀 모형
-> -3.606 + 0.024 x1 + 1.632 x2
- deviance 이탈도 : 선형 회귀 모형의 잔차 제곱합을 일반화한 개념. 정규분포를 따른다고 한다면 카이제곱 분포를 따름.

로지스틱 회귀 모형의 유의성 검정
- H0 : log (pi/(1-pi) = beta0 vs H1 : log(pi/(1-pi) = beta0 + beta1x1 + beta2x2
=> 정리하면 H0 : beta1 = 0, beta2 = 0 vs H1: 적어도 하나는 0이 아니다.
- 두 이탈도의 차이가 유의한지 보면됨.

'수학 > 통계' 카테고리의 다른 글
| 다변량분석 - 2. 다변량 분석과 데이터 시각화 (0) | 2020.11.03 |
|---|---|
| 다변량분석 - 1. 다변량 분석과 R 기초 (0) | 2020.11.03 |
| 회귀모형 - 4. 회귀 모형 만들기 (0) | 2020.10.30 |
| 회귀모형 - 3. 회귀 모형에서 변수 선택 (0) | 2020.10.30 |
| 회귀모형 - 2. (다)중회귀모형 (0) | 2020.10.30 |