집밖은 위험해

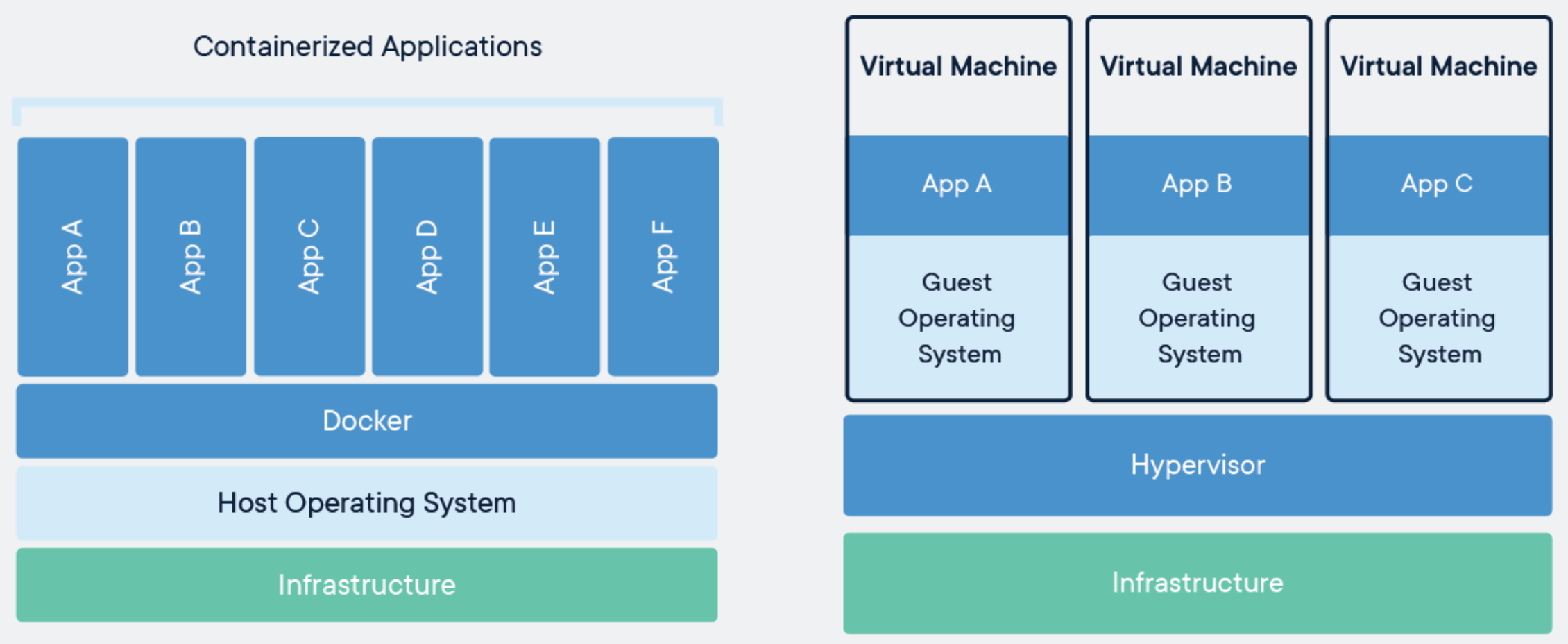
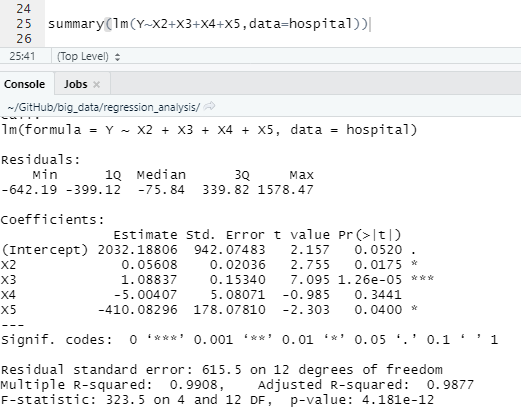
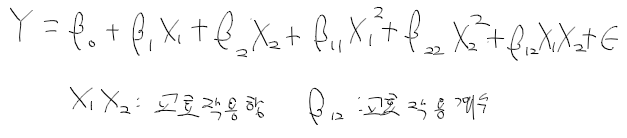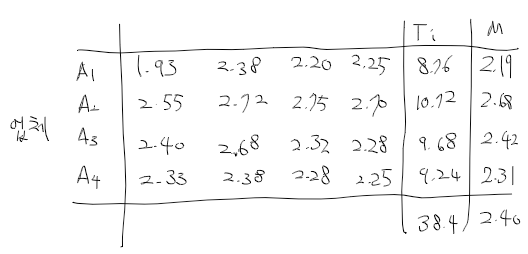최근 푹 쉬고 나서 빅데이터 공부하면서 다시 조금식 페이스를 찾아가고 있다.

어쩌다가 IT분야를 시작하게 되었는지 쓰고 싶어지면 남기고

그 동안 과정을 한번 글로 정리하고 싶었는데 적어보려고 한다.

대학교를 그만둔 직후에는

프로그래밍 분야에 어떤게 있는지 잘 몰랏었다.

2016년 당시에는 검색해보면 그나마 가장 많이 나왔던게 웹개발 국비 과정이라

웹 개발자에서부터 시작하게 되었다.

자바, 데이터베이스, JSP, 스프링 프레임워크 등을 배우면서

프로그래밍 언어의 기본적인 틀과 자료구조

데이터베이스를 어떻게 설계하는것인지

HTTP 프로토콜 요청에 따라 웹서버가 어떻게 처리를 하는지

JDBC로 자바와 데이터베이스 사이 연동하는 과정

데이터베이스 데이터를 자바 클래스에 맞추고

프론트 단에 넘겨서 화면에 보여주기 등

혼자서 기본적인 계층형 게시판 같은 웹 어플리케이션을 만들수 있을 만큼 실력을 쌓았고

당시 팀프로젝트에선 팀원들의 개별적인 문제와 각자의 모듈을 합쳐 정상적으로 돌아가도록 했었다.

 중기청 SW 대회에서 혼자 모의 주식게임 웹어플리케이션을 제출하여 특별상을 수상하고,

작은 스타트업에 취업을 하게 되었다.

거기선 입사한 당시에는 사수는 없었고, 클라우드 플랫폼에 올라간 웹 서비스를 다루어야 했다.

내가 다니던 학원에서는 리눅스를 하지 못해 그 즈음 리눅스를 처음 만지기 시작해서,

포트포워딩, 클라우드, 그리고 ORM 객체 관계 모델 이었던가 데이터베이스 테이블 한 데이터를 객체에

매핑 시켜서 다루는 기술들을 공부해나갔다

당시 웹 개발을 하는 신입들 중에서 못하는 편은 아니었다고 생각은 하지만

내 성향상 업무를 잘 수행하지 못하고, 그만 두고 말았었다.

그 시점에서는 당시 지금처럼 노드나 리액트같은 js들이 많이 사용되기 전이었다보니

기본적으로나마 ERD를 설계해서 데이터베이스 서버를 돌리고,

스프링 웹어플리케이션 MVC 모델이나, 부트스트랩 같은 프론트앤드를 다루기는 했으니

이 만큼이면 웹에 대해 전반은 다뤘다고 생각했었고,

깊이 들어간다면 더 깊이 들어갈수 있었더라도

더 이상 웹분야에 공부할 필요성을 느끼지 못하고 컴퓨터에 대해서 제대로 공부하고 싶어졌었다.

대학교를 자퇴하고나서 고졸이던 나는 학점은행제를 준비하고 있었으나 아직 학점이 부족했었고,

국가장학금을 받을걸 생각하고 폴리텍에 입학하여 컴퓨터 과학에 대해 제대로 공부하기 시작하였다.

컴퓨터 개론, 디지털 회로 기초 같은 과목들을 들으면서 컴퓨터 기본 이론을 공부하고,

C언어와 소켓 통신을 별도로 공부했었다.

하지만 당시 폴리텍 수업만으로는부족해서 다른 과정도 생각하고 있었다.

우리가 가장 밀접하게 사용되는 프로그램이라 하면 웹, 모바일, 임베디드 정도라 생각하고 있었는데

웹에서도 하이브리드로 모바일 어플리케이션을 만들수 있었으니,

전자와 임베디드 분야를 해보고 싶던 나는 임베디드 학원을 다니게 되었다.

그 곳에서의 과정은 임베디드에 필요한 전반을 다루다보니

C/C++에서부터 데이터베이스, 리눅스, 라즈베리파이, 디바이스드라이버, QT GUI 정도를 다뤘었는데

이전부터 C나 데이터베이스, 리눅스는 조금씩 공부해온게 있었던 덕분에 조금은 수월하게 들을수 있었다.

특히 QT를 배우면서

서버단, 프론트단, 데이터베이스 까지 고려해야하는 웹과는

다르게 생각보다 쉽게 데스크탑 어플리케이션을 만들수 있어서 신기하더라.

그리고 이 즈음 학사 학위를 받을 만큼 학점이 준비되어 학점은행제로 학위를 받았다.

임베디드 분야도 조금 공부하고, 학사 학위를 받았지만 약간 욕심이 생겨 대학원에 가고 싶었는데

제대로 된 대학원에 들어갈수 있을거란 자신이 없었었다.

당시 나는 제대로 된 대학을 나와 학사 학위를 받은게 아니라 전공 지식도 없고

웹/임베디드 학원 다니면서 배운 개발 지식이 전부다 보니 대학교 연구실 받아주는곳이 있을까 싶더라

그리고 군대 문제도 있다보니 전산병으로 가야되지않을까 고민하던 시기였다.

평소 그렇게 고민하면서 검색하던 중 한 대학원을 찾았는데

거기서 국비 지원으로 등록금도 안들고, 미필자의 경우 전문연구요원으로 병역 문제도 해결해준다고 하더라

너무 좋은 소리만 하고, 비전공자가 들어갈수 있는 대학원이야 제대로된 곳은 아니었다.

몇 번 가보고 나서는 가지 말려고 주저하기는 했었으나 교수는 계속 연락하지

부담은 안되고, 공부는 더하고 싶고, 제대로 된 곳에 갈 자신이 없었던 나는 바보같은 선택을 하고 말았다.

내가 들어간 당시에는 본교 재학생들도 다 도망가고 안오는 곳이라

제대로된 연구 성과나 선배없이 밑 바닥에서 시작했다.

거기선 딥러닝, 드론, 자율주행차 하게 되었는데

당시에는 공학/수학적 지식이 전혀 없다보니

아무 생각없이 시중에 파는 교재를 보거나 최대한 검색하면서 공부해나갔다.

그러다보니 다른 대학원의 연구 성과 같은걸 보면 너무 부러웠지만 어쩔수가 없었다.

한번은 의존 관계에 대한 개념 자체가 없는 상태에서 자율주행 오픈소스를 빌드하는데

자꾸 빌드 실패가 났었다.

나는 아무리 고치려 해도 빌드 실패하는 이유를 찾을수가 없었고,

2주동안 빌드로 해매면서 눈물나더라

여러 분야를 조금이나마 공부한 지금은 

당시 교수가 왜 이런식으로 시켯을까  많은 생각이 든다.

그때는 암만 미워도 내발로 들어온 곳인데 좋든 나쁘든 성의것 했고 트러블도 있었지만 졸업은 할 수 있었다.

비전공자 치고는 나름대로는 열심히 했다고 생각해

그 이후로는

이 블로그를 만들고

대학원에서 삽질하느라 못했던 공부를 잔뜩하다보니

벌써 2020년이 끝나가고 있다.

지금까지

전기, 전자, 대학수학, 공업수학, 선형대수, 임베디드, 확률, 통계, 제어, 신호처리 등

이것 저것 공부하면서

개념이 확실하게 이해된 부분도 많아졌지만

잊은 내용도 많고, 더 공부해야할게 보인다.

그런데 이러면 끝이없고

이렇게까지 공부할 필요없이

어느 분야든 취업해서 그 분야에 필요한 도메인 지식과 노하우를 익혀나가는것도 길이라 생각한다.

아직 정해진건 없고

적어도 올해 빅데이터 분석기사만 따고 잘 마무리 했으면 좋겠다.

그리고 곧 글 1000개 달성 !

실습 과제물...

1. fluentd와 몽고db로 로그 취합하는 시스템 구축

2. jupyter/datascience-notebook or jaimeps/rl-gym 등 데이터 사이언스 관련 컨테이너를 public cloud에서 구동하고 jupyter에서 접속한다.

3. pytorch를 설치한 이미지로 컨테이너를 구동한다.

www.docker.com/resources/what-container

도커란 무엇인가

컨테이너

- 의존성과 패키지코드가 함께 있는 추상화

- 각 머신처럼 동작 가능. os 커널은 공유

클라우드 컴퓨팅

- aws, 에저, 구글 클라우드 엔진

 => 구글 클라우드 엔진이 후함

console.cloud.google.com/

도커 설치하기 

curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add -

sudo add-apt-repository \
   "deb [arch=amd64] https://download.docker.com/linux/ubuntu \
   $(lsb_release -cs) \
   stable"

 $ sudo apt-get update
 $ sudo apt-get install docker-ce

ref: docs.docker.com/engine/install/ubuntu/

도커에는

이미지와 컨테이너가 있다..

컨테이너 들어오기

docker run -i -t ubuntu:14.04

* -i : interactive

* -t : terminal

기존 환경에서 우분투 14.04 컨테이너로 들어왔다.

exit 명령의 경우 컨테이너 자체가 종료된다.

컨테이너

어플리케이션 실행하고 싶은데 실행하기 위한 공간

ctrl pq를 하면 다시 컨테이너 밖으로 나온다..

(exit와 달리 컨테이너 종료 x)

다시 캡처해서 보면

아까 컨테이너가 살아있다.

docker ps -a

exit 시킨 컨테이너도 나온다.

docker rm {id, name} 컨테이너 삭제하기.

삭제하려했더니 동작중이라 한다 

docker stop id/name

stop부터 해주고 다시 삭제

stoic_williamson 컨테이너 삭제 ok

centos 이미지 가져오기

docker pull centos:7

docker image ls

- 가지고 있는 이미지 목록 보기

-> 우분투 버전 14.04와 센토스 7이 추가되어있다.

docker run -it centos:latest

센토스 컨테이너에 들어왔다가

다시 컨트롤 pq로 나오자.

docker ps해보면 centos:latest가 돌아가고있다.

docker container prune

쓰지 않는 컨테이너 지우기

docker attach 아이디/이름 : 다시 컨테이너 들어가기

이미지 생성하기

docker create -it --name (이름) (기본 이미지;centos:latest)

다시 시작하기

docker start 이미지/id

웹서버 돌리기

컨테이너 80포트와 호스트 80포트 바인딩 시켜서 돌리기

컨테이너는 휘발성

이미지를 만들자.

놓침 ㅠㅠ

도커 이미지

- 레지스트리에서 관리

 public, private, docker hub 같은대

wordpress 돌리기'

먼저 워드프레스용 db 부터 준비

mysql 돌리기, 환경변수도 다음과같이 수행

docker run -d --name wordpressdb -e MYSQL_ROOT_PASSWORD=password -e MYSQL_DATABASE=wordpress mysql:5.7 

'

https://hub.docker.com/_/mysql

wordpress db가 잘돌아가고있다..

'

이런식으로 컨테이너에 들어갈수도 있다.

docker exec -it wordpressdb /bin/bash

wordpress 컨테이너 돌리기

docker run -d -e WORDPRESS_DB_PASSWORD=password --name wordpress --link wordpressdb:mysql -p 80:80 wordpress 

wordpress와 wordpressdb가 잘 동작중..

워드프래스 페이지도 잘나온다.

둘다 종료하려면

docker rm -f wordpress wordpressdb

종료했다가 다시 실행하면 다날라간다..

컨테이너 -> 읽고 쓰기 가능

이미지 -> 안변함

이미지 추가, 삭제, 변경? => 사실 컨테이너에서 삭제, 추가, 변경됨. 컨테이너는 날라간다

컨테이너의 볼륨을 사용하도록 지정??

호스트의 볼륨을 공유 

-v 호스트 경로:컨테이너 경로

=> 호스트의 /home/wordpress_db에서 쓰면 컨테이너의 /var/lib/mysql이 반영

 docker run -d --name wordpressdb_hostvolume -e MYSQL_ROOT_PASSWORD=password -e MYSQL_DATABASE=wordpress -v /home/wordpress_db:/var/lib/mysql mysql:5.7

- 호스트 경로에 컨테이너의 파일이 공유

워드프래스도 돌리자

docker run -d -e WORDPRESS_DB_PASSWORD=password --name wordpress_hostname --link wordpressdb_hostvolume:mysql -p 80:80 wordpress

설정도 다하고 껏다 키면

원래 컨테이너 내용들은 다 사라져야 정상이지만

호스트 볼륨에 db를 저장해놔서 껏다 켜도 사라지지 않는다.

로그 처리보기

 docker run -d --name mysql -e MYSQL_ROOT_PASSWORD=1234 mysql:5.7

는 잘실행되지만

 docker run -d --name no_password_mysql mysql:5.7

비밀번호를 주지않는 경우 ps가 존재하지 않는다.

docker logs 이름을 주면 로그가 나온다.

docker logs no_password_mysql을 하면

mysql_root_password를 안준게 문제라고 나온다.

컨테이너 정보보기

docker inspect 이름

도커 이미지 숙지하기

컨테이너는 날라가지만 이미지는 만들수있다.

 docker run -it --name commit_test ubuntu:14.04

컨테이너에서 파일하나 만들어주고 나오자

컨테이너는 동작중

이미지 만들기

docker commit -a "이름" -m "메시지" 컨테이너명 저장소:태그

과제하기

2. jupyter/datascience-notebook or jaimeps/rl-gym 등 데이터 사이언스 관련 컨테이너를 public cloud에서 구동하고 jupyter에서 접속한다.

도커허브에서 풀 커맨드 카피

이미지 다운받고

docker pull jupyter/datascience-notebook

주피터 이미지를 돌리고, 쉘로 들어가서 외부 접속을 허용시켜주자

주피터 설정 파일에 들어가서

#c.notebookapp.allow_origin="" 는 주석을 지우고 별표

c.notebookapp.allow_origin="*"

내가만든 이미지를 확인해보니 ip 주소가 172.17.0.2 이므로

8888포트로 들어갈수있도록 방화벽도 오픈하자.

토큰 안나오개 하려다 망해서 그냥 패스

---------------------------------------

 docker run -d -p 8888:8888 -v /home/jupyter:/home/jovyan/work --name juyter jaimeps/rl-gym

로그서 토큰보고 들어가자

3. pytorch를 설치한 이미지로 컨테이너를 구동한다.

 정리하기 귀찬다.

jupyter/datasicn블라블라 컨테이너에들어가서

pip로 torch 설치

pip install torch

토치 설치된 컨테이너를 이미지로 만들어주자 docker commit

* docker commit -a "작성자" -m "메시지" 이미지만들패키지 [저장소명:태그]

docker commit -a "jdo" -m "add torch" jupyter jdo/jupyter:first

기존의 컨테이너는 지워주고

docker rm -f jupyter

새로 만든 이미지를 실행하자

docker run -d --name jupyter -p 8888:8888 -v /home/jupyter:/home/jovyan jdo/jupyter:first

주피터 컨테이너에 동작하면, 이 컨테이너의 배쉬 셸로 들어가자

docker exec -it jupyter /bin/bash

python 명령어로 python 인터프리터 실행

import torch

print(torch.__version__)

설치된 토치의 버전 확인까지 하면 끝 !

기존의 회귀 모형 regression model

- 기본 가정 : 오차 등분산성, 모형의 선형성, 오차의 정규성

반응 변수 Y가 정규 분포가 아닌경우

- 오차의 등분산성 위배 -> 분산안정화변화로 해결

- 오차의 정규성이 위배(오차가 정규분포를 안따를떄) : 일반화 선형 모형

일반화 선형 모형를 사용하는 경우

- 반응변수 Y가 정규분포를 안따르는 경우

 ex. 반응변수가 비율을 나타내는 경우, 반응변수가 양의 개수를 나타내는 포아송 분포를 따르는 경우

일반화 선형 모형 generalized linear model

- 반응 분포가 정규 분포 뿐만아니라, 이항분포, 포아송분포,

  감마 분포와 같은 지수족 분포를 따를때 회귀 모형 형태로 확장된 모형

* 회귀모형의 한계를 극복함.

일반화 선형 모형의 구성성분 세가지

- 반응 변수의 분포

- 선형 예측자 eta = beta_0 + beta_1 X = g(mu)

- 연결 함수 g(mu) = log(mu)

예시 : 1983 ~ 1986년 동안 호주에서 에이즈로 인한 사망자수

x : 1983년 1월부터 3개월 단위 경과 기간

y : 사망자수

선형 모형의 일반화 선형 모형으로 확장

지수족 분포 the exponential family of distributon

- 반응변수 분포가 지수족 분포를 따를때 일반화 선형 모형 사용

- 확률 밀도함수 f(y;theta;phi)와 같이 표현되는 분포로 아래와 같음.

- theta : 평균 mu의 함수로 정준 모수 canonical parameter

- phi : y의 분산과 관련되고, 평균과는 독립인 산포모수 dispersion param

- w : y 분포 가정에 따라 사전에 알수있는값

선형 예측차 eta linear predictor 

- 설명변수들의 선형 결합

연결 함수 link function

- 선형 예측자와 반응변수의 평균 사이 관계를 eta가 되도록 만들어주는 함수 g()

지수족 분포의 정준 연결 canonical link

로지스틱 회귀모형

- 반응 변수가 이항 자료인 경우 사용

=> 로지스틱 회귀모형 : 로짓 함수가 선형 연측자가 되는 모형.

ex. 날다람쥐의 출현 자료( 독립 : con_metric ,  p_size_km, 종속: 1 또는 0)

 => y = occur, 1=yes, 0= no => 이항분포를 따름

- 로지스틱 회귀 모형

 -> -3.606 + 0.024 x1 + 1.632 x2

- deviance 이탈도 : 선형 회귀 모형의 잔차 제곱합을 일반화한 개념. 정규분포를 따른다고 한다면 카이제곱 분포를 따름.

로지스틱 회귀 모형의 유의성 검정

- H0 : log (pi/(1-pi) = beta0 vs  H1 : log(pi/(1-pi) = beta0 + beta1x1 + beta2x2

 => 정리하면 H0 : beta1 = 0, beta2 = 0 vs H1: 적어도 하나는 0이 아니다.

- 두 이탈도의 차이가 유의한지 보면됨.

회귀 모형 regression model

- 단순 회귀 모형 : 독립변수와 종속변수간에 선형적 관계를 갖는 경우 사용

- 다항 회귀 모형 : 독립변수와 종속변수간에 비선형적인 관계를 같는 경우

다항 회귀 모형 polynomial regression model

1. 독립변수가 하나인 경우 이차 다항 회귀 모형

2. 독립변수가 2개 인경우 이차다항회귀모형

다항회귀모형 예제 1

1. 데이터 로드, 플롯

- 연도별 교통범죄발생률과 승용차보급률

- 플롯시켰더니 약간 비선형적

 => 2차 다항 회귀모형으로 만들어보자.

* attach(데이터프레임). => plot시 데이터프레임$ 를 생략할수 있음

2. 모형 생성 

- 구한 이차다항회귀모형은 아래와 같다.

다항회귀모형 예제 2 : 1990~1992년까지 마라톤 대회 5km 구간별 평균속도

1. 데이터 로드, 플롯

- 데이터 형태를 보니 3차 다항회귀모형을 만들자

2. 모형 추정

- beta0 ~ 3까지 pvalue가 매우 작음 => 유의

가변수 회귀모형 dummy variable regression model

- 독립변수에 이산형 변수가 포함되어있는 경우에 사용

- 가변수 dummy variable, indicator variable ; 두가지 값을 갖는 변수

- 예시 : 비누 생산공장에서 부스러기양과 공정속도

=> 교호작용을 고려한 모형

=> 교호작용이 없는 모형

R에서 실습

1. 데이터 읽고 산점도 그리기

- line0와 line1은 기울기는 차이없고, 공정에 따라 차이가 있어보임

=> 교호작용이없는 모형을 고려

2. 모델 생성

- 교호작용이 없는 모형

- 두 생산 라인은 beta2만큼의 차이가 존재

 H0 : beta2 = 0을 기각한다면 => 두 생산공정에 차이가 존재

- p value가 매우 작으므로 두 생산 공정에 차이가 존재하며, 차이는 53정도.

- adjust R2는 0.9352로 유의

3. 모델 만들기

- 교호작용을 고려한 경우

- X:Dline1 의 경우 pval이 0.18로 유의수준보다 크므로 유의하지 않음.

 => 교호작용을 고려하지 않은 모형이 적합.

변수 선택과 기준/방법, 다중 공선성

다중 회귀 모형

- 여러개의 독립변수에 의해 종속변수 y에 주는 영향을 함수 식으로 표현한것

변수선택 variable selection problem

- 많은 설명 변수 중에서 모형에 포함시킬 변수를 결정하는 것

다중공선성 multicollinearity

- 모형에 포함되는 설명변수들 사이 연관성이 존재하는 경우 모형의 안정성과 신뢰성을 떨어트림

=> 공선성, 다중공선성

- 두 설명변수 X1, X2가 상수 c0, c1,c2에 대해 다음 관계를 가지는 경우

  -> 두 변수 사이에 완벽한 공선성(exact collinearity)가 있음

ex. X1 + X2 = 100인경우 X2는 X1으로 결정됨

다중공선성 multiconllinearity

- 설명변수가 2개가 넘는 경우 다음과 같은 관계가 성립하거나 근사적으로 성립할시

 => 설명변수들 사이에 다중 공선성 multiconllinearity이 존재

- 설명변수 Xh와 나머지 설명변수간의 결정계수(다중상관계수의제곱) Rh^2이 다중공선성의 정도를 나타냄.

다중 공선성에 대해 의심이 드는 경우

- 설명변수의 표본 상관행렬에서 상관계수가 크게 +-1에 가까울떄

- 설명변수를 모형에 추가/제거시 추정된 회귀계수의 크기나 부호에 큰 변화를 줄때

- 새 자료를 추가/제거시 추정된 회귀 계수의 크기나 부호에 큰 변화를 줄때

- 중요하다고 생각되는 설명변수의 검정 결과가 유의하지 않거나 신뢰구간이 넓을때

- 추정된 회귀 계수의 부호가 과거의 경험이나 이론적인 면에서 기대되는 부호와 상반될때

분산팽창인자 VIF; variance inflaction factor

- R_j^2 : Xj를 반응변수로 보고 나머지 설명변수에 대한 결정 계수

- k개의 VIF_j 중 가장 큰 값이 5~10이 넘으면 다중공선성 있다고 판단.

병원 데이터를 이용한 예제

1. 데이터

Y : 월간 의사 연 근무시간

X1 : 일평균 환자수

X2 : 월간 Xray 초라영 횟수

X3 : 월간 이용병석수

X4 : 해당지역 병원이용가능인구 / 1000

X5 : 평균입원일

2. 회귀모형 구하고 보기

- X1 일평균환자 : 늘어날수록, 근무시간 Y는 늘어날탠대 -15.85167이 나옴

- X4 병원가능인구가 늘어날수록, 근무시간 Y는 늘어나야하나 -4.219가 나옴.

- X5 평균입원일이 늘어날수록, 근무시가이 늘어야하나 -394...

=> 독립변수간에 다중공선성이 존재가 예상되며, 분산 팽창인자 등에 의한 진단이 필요.

3. 분산팽창인자 계산하기

- X1, X2, X3, X4의 분산팽창인자를 계산해보면 5이상으로 다중 공선성 문제가 존재

4. 독립변수간 상관관계 보기

- cor()함수 : 상관계수 행렬

- X5를 제외한 X1 ~ X4까지 강한 선형 상관관계가 존재. x5를 제외하고 대부분 1에 가까움.

설명변수 X1을 제외한 경우 모형을 보자

1. summary

- R2는 차이없음

- 추정된 회귀계수의 표준 오차는 조금 줄어듬

2. 분산팽창지수 보기

- x1이 포함되었을때보다 크게 줄어듬

모형 선택 기준 - 결졍 계수

-  R_p^2는 k개의 설명변수중에서 p개의 설명변수로 구성되는 모형에서 아래처럼 정의

- 결졍 계수는 설명 변수가 추가되어 p가 커질수록 증가

 =>모든 변수가 포함이 다된 모형(p=k)일때 최대되도록 증가

= 최대 결정계수 값인 모형을 선택은 의미 없음.

모형 선택의 기준 - 수정 결정계수 adjusted coefficient of determination

- 결정계수 R_p^2의 문제를 보완하기 위한 방법.

- SS를 그대로 쓰기보다 자유도로 나누어 조정과정을 거침

- bar R_p^2는 설명변수가 증가해도 항상증가하지않음

=> 모형 선택시 수정 결정계수가 큰것을 사용하자

모형 선택 기준 : mallows Cp 통계량, AIC

- k개의 독립변수 중에서 p개의 변수를 선택할때, C_p가 최소가되는 모형을 선택

- AIC : 작은값을 갖는 모형을 선택

변수 선택 방법

- 모든 가능한 회귀 all possible regression

- 앞에서부터 선택 forward selection

- 뒤에서부터 선택  backward elimination

- 단계별 회귀 stepwise regression

1. 모든 가능한 회귀

- 독립변수가 k개 있으면 2^k -1 개의 회귀모형을 다뤄보자

 => k가 커질수록 계산량이 급격히 늘어남

1.1 데이터 로드

- 독립변수 4개,

1.2 모든 가능한 회귀 수행

- leaps 패키지의 regsubsets()함수

- 선택 알고리즘 : exhaustive

- 독립변수가 1개인 경우 가장 좋은 모형은 X4

- 독립변수가 2개인경우 가장 좋은 모형은 X1, X2

- 독립변수가 3개인 경우는 X1, X2, X4

1.4 구체적인 통계량을 보기

- 아래의 통계량을 정리해보면 X1, X2, X4가 사용된경우 조정된 R2가 가장 크고

- X1, X2인 경우 Cp가 가장 작다

- Cp는 작을수록 좋고, 조정된 R2는 클수록 좋다.

=> X1X2 나 X1X2X4 선택

2. 앞에서부터 선택 forward selection method

- k개의 설명변수 중에서 가장 영향이 큰 변수부터 하나씩 선택

- 더이상 중요한 변수가 없다고 판단할때 선택 중단하는 방법

2.1 R에서 실습

- AIC기준으로 수행. AIC는 값이 작을 수록 좋음.

- X3은 없는게 나으므로 X4, X1, X2를 선택

뒤에서부터 제거 backward elimination method

- 모든 독립변수를 사용한 모델에서부터 기여도가 작은 변수를 제거해나가는 방법

단계별 회귀 stepwise selection

- 앞에서 선택법에 뒤에서 제거법을 가미

- 새 변수가 추가될떄마다 기존 변수가 제거 될 필요가 있는지 검토하여 선택

Y~1에서 

+X4하는 경우 AIC

~ +X3하는경우 AIC

=> X4를 추가하는것이 AIC가 가장작다 

Y~X4에서 

+X1하는경우 / +X3하는경우 /  추가 x/ +X2 경우 / -X4 경우

=> +X1일떄 AIC가 가장적다. => X1 추가

...

더하는 경우와 빼는 경우를 동시에 고려

데이터 분석 방법 복습

이산형

- 일원배치법

- 이원배치법

연속형

- 회귀모형

(다)중 회귀모형 multiple regression model

- 종속 변수의 변화를 설명하는데 두 개 이상의 독립 변수가 사용되는 회귀 모형

- 선형인 경우 다중 선형 회귀 모형

독립변수가 k개인 다중 회귀 모형

- beta0, ..., betak : 모집단 회귀 계수

- epsilion i : Yi를 측정시 오차

독립변수가 2개인 다중 회귀 모형

- 벡터로 나타내는 경우

다중 회귀 모형 - 행렬 + 독립변수 2개

상점의 총 판매액 자료를 이용한 다중 회귀 분석

- 독립변수 : 광고료 x1, 상점크기 x2

- 종속변수 : 총 판매액 y

다중 회귀 모델 - 최소제곱법

- 행렬을 이용하면 쉽게 추정치 beta를 구할 수 있다.

- 다중 회귀 모델

- 오차에 대한 식

- 오차 제곱 합에 대해서 정리하면

- beta에 대하여 미분하고, hat beta(estimate beta)를 구한다.

R로 다중 회귀 모델 구하기

- 결과

잔차 residual

- 관측값 Yi - 추정된 회귀값 hat Yi

- 추정값과 잔차 사이의 관계

햇 행렬 hat maixt

- 햇 행렬의 정의

- 다음 성질을 만족하는 멱등행렬 idempotent matrix

회귀 방정식의 신뢰성 보기

- 분산분석표에서 F 검정

- 결정계수

- 잔차 평균 제곱

총 제곱합 SST

잔차제곱합

회귀제곱합

변동 분해

중회귀 분산분석표

- 검정통계량 F0 : 회귀방정식이 유의한가를 검정하기 위한 검정 통계량

- H0 : beta1 = beta2 = ... = 0   vs H1 : 하나의 betai != 0

- 유의수준 alpha에서 F0 > F(k, n-k-1;alpha) 인 경우 귀무가설을 기각 => 회귀방정식이 유의

- R에서 F0에 대한 유의확률 Pvalue가 유의수준 alpha보다 작다면 귀무가설 기각함 

R로 회귀 식 구하기

- 분산분석표로 보기

결정계수 coefficient of determinantion

- 이 회귀 식이 얼마나 설명력이 있는지 나타내는 값 R^2

중 상관계수 mutiple correlation coefficient

- 단순 회귀에서 결정계수 R^2 = 두변수의 상관계수 제곱과 같다. corr ^2

- 중회귀 모델에서 결정계수 = 반응변수 Yi와 추정값 hat Yi의 상관게수의 제곱

=> 다중회귀모델에서 결정계수의 제곱근

예측방법론

- 예측에는 주관적 예측과 객관적 예측이 있음

- 데이터 기반 예측 -> 객관적 예측

- 시계열 특성과 예측 모형을 보고 R 구현

회귀 분석 regression analysis

- 독립변수와 종속변수 사이의 함수 관계(모형)을 구하는 통계적 분석 방법

- 독립 변수 independent variable, 설명변수 explanatory variable: 영향을 주는 변수 x

- 종속변수 dependent variable, 반응변수 response variable : 영향을 받는 변수 y

회귀 용어의 유래

- 영국의 우생할자 galton이, 부모콩의 무게를 x 자식콩이 무게를 y로 산점도를 그려 관계를 살펴봄

 => 자식의 무게는 평균 무게로 회귀(되돌아 가려는)하려는 경향을 발견 => 피어슨이 분석하여 발표

단순 회귀 모형 simple regression model

- 가장 간단한 회귀 모형

- 독립 변수와 종속 변수 사이에 선형적 관계를 표현함

- Yi : i번째 측정된 반응변수 Y의 값

- beta 0 : 절편 회귀계수

- beta 1 : 기울기 회귀계수

- Xi = i번쨰 상수 X값

- epsilon i = i번쨰 측정된 Y의 오차항

회귀선 regression line

- 표본으로 모형식을 추정하여 구한 직선. 추정된 회귀 직선, 회귀선이라 함.

-b0와 b1은 beta0와 beta1의 추정값

- hat{Y}는 E(Y)의 추정값

- b0는 회귀절편 intercept

- b1은 X가 한단계 증가할떄 hat Y의 증가량으로 기울기 slope

- 회귀 계수 b0, b1을 구하는 방법 => 최소제곱법

최소제곱법 method of least square LSM

- 회귀 모델이 다음과 같이 주어질떄

- 오차 항 제곱 합은 아래와 같다.

- > S를 beta0과 beta1에 대해 각각 편미분한 결과가 0이 되는 beta0와 beta1를 b0와 b1로 함.

-위 식을 정리하면 아래와 같으며, 이 식을 정규 방정식 normal equation

- b0와 b1에 대하여 정리

선형 회귀 모델 예제 - 광고료와 총판매액

- 기울기는 2.6087으로 추정 p value가 매우 작으므로, 귀무가설 기각 -> 유의한 결과를 보임

- 절편은 -2.2696으로 추정

잔차 residual

- Xi에서 관측된 값 Yi와 추정된 hat Yi사이 차이

- 잔차의 합은 0

- 잔차의 제곱합은 최소

- 관찰값 Yi의 합과 추정된 hat Yi는 같다.

- R에서 확인하기

회귀 모형의 정도

- 구한 회귀 모형이 얼마나 좋은가?

분산 분석표에 의한 F 검정

- 변동 분해하기

 회귀제곱합의 자유도는 독립변수가 1개이므로 

 총 데이터 수가 n개에서 평균에 대한것을 빼므로 n - 1

 => 잔차제곱합의 자유도는 n - 2

분산분석표를 이용한 F 검정

- 변동을 분해한 표

- 가설 검정

- F0 > F(1, n-2; alpha) 이면 유의수준 alpha에서 귀무가설을 기각 => 회귀 직선이 유의하다

- R에서 유의 확률 p value를 제공. pvalue < alpha이면 귀무가설 기각

R에서 분산분석

- p value가 0.001487로 매우 작으므로 귀무가설을 기각

결정계수 coefficient of determination

- 회귀선이 어느정도의 설명력을 가지고 있는가를 나타내는 지표

- R^2는 0 ~ 1

- X와 Y 사이 높은 상관관계를 가질수록 R^2 는 1에 가까워짐

-> 0에 가까우면 유용성이 떨어지는 회귀선

- 회귀선으로 설명되는 변동/총변동이므로 회귀선의 기여율이라고도함.

추정값의 표준 오차 Mean Squared Error

- 잔차 평균 제곱 MSE는 오차 분산 sigma2의 불편추정량.

- sqrt(MSE)로 표준 오차를 구함

분산분석 -> 요인의 수준이 이산형(100, 120)에 따른 종속변수의 영향

회귀분석 : x가 이산이 아닌 연속인경우 분석 방법

공분산분석 : x가 이산형인것도 있고 연속형인것도 두개다 있는 경우

회귀분석 regression analysis

- 독립변수들과 종속변수 간에 관계를 함수식으로 정리하여 분석하는 방법

- 독립/종속변수는 연속값

- 단순 회귀 simple regression : 독립변수가 하나

- 다중 회귀 multiple regression  :독립변수가 여러개

다중 선형 회귀 multiple linear regression

다항 회귀 모형 polynomial regression model

상관계수 correation coefficient

- 두 변수간에 선형적 상관관계에 대해서 나타냄

- 1에 가까우면 양의 상관관계

- -1에 가까우면 음의 상관관계

- 0에 가까우면 선형적 상관관계가 존재하지 않음

단순 선형 회귀 분석 simple linear regresion analysis

- 모형 model

- 관측치 measurements

- 추정식 estimator

- 잔차 residual

최소제곱법 least squared method LSM

다음 데이터가 주어질떄 단순선형회귀를 수행하라

R로 테스트

- 추정량 -0.28928

- 기울기 0.45664 -> pvalue = 3.21e-07로 매우작다 =>유의하다.

- R-squared : 0.9338로 유의함

회귀선의 유의성 검정

- 두 변수 사이에 회귀 관계가 없다면 beta1는 0이되어 다음의 식이 성립합.

- 총제곱합과 잔차제곱합, 회귀제곱합 사이의 관계

결정계수 coefficient of determination R^2

- 회귀식이 얼마나 의미있는지

- R square가 크면 클수록 유의하다.

- 회귀 계수 beta1의 유의성

 -> H0: 회귀관계가 없다. vs H1 : 회귀관계가 있다.

     H0: beta1 = 0 vs H0: beta1 !=0

분석분석표

- 회귀분석의 유의성 검정

분산분석표 분석

유의확률 pvale가 매우 작으므로 h0 기각. 매우 유의

공분산 분석

- 분산분석 + 회귀분석

- 일원 배치 분산분석 : 기계(3대) -> 섬유 제품 강도

- 이원 배치 분산분석 : 기계(3대), 원사두께(얇음,두꺼움) -> 섬유제품 강도

- 공분산 분석 : 기계(3대), 원사 두께(연속적인값, 공변수 covariate) -> 섬유제품 강도

공분산 분석 예시

- 일원배치 예시 : 두개의 사료 (A,B) => 섭취후 체중 y

- 공분산 분석 예시 : 두 사료(A,B), 초기체중 x(연속적인값) => 섭취후 체중 y

이원배치법

- 2개의 요인(독립변수 A, B)와 반응 변수(종속변수) 사이의 관계를 알아보기위한 실험계획

- 독립 변수는 불연속, 종속 변수는 연속적인 값

- 반복이 없는 경우와 있는 경우가 존재

- 반복하는 경우 두 요인간 상호 작용 효과를 검출 가능

이원배치법에서 효과

- 주 효과 main effect : 요인 A의 수준간 차이가 존재하는가

- 상호 작용 효과 interection effect(교호 작용효과) : 요인 A의 서로 다른 수준에서 요인 B의 주효과가 다른가

실험의 랜덤화

- 완전 확률화 계획법 : 두 요인 수준 조건에 순서를 주고, 랜덤한 순서대로 실험

이원 배치법 고정모형(A, B 고정요인- 모수인자)

- 반복의 장점

  인자 조합의 효과를 실험 오차와 분리하여 구할수 있음

  교호작용을 분리하여 검출할수 있어 주효과에 대한 검출이 개선됨

  실험 오차를 구할 수 있음

- 이원배치법의 자료구조

반복이 있는 이원배치 모수모형 (A, B 두인자 모두 고정, 모수인자인경우)

검정 가설

1. 인자 A에 대한 가설

 H0 : alpha1 = alpha2 = ... = 0 ->인자 A의 수준간 효과 차이 없다.

 vs H1 : 적어도 하나의 alphai는 != 0 -> 인자 A의 수준관 효과 차이 있다.

2. 인자 B에 대한 가설

 H0 : beta1 = beta2 = ... = 0 -> 인자 B의 수준간 효과에 차이가 없다

 vs H1 : 적어도 하나의 betai는 != 0 -> 인자 B의 수준간 효과 차이 존재

3. 인자 A와 B의 교호작용에 대한 가설

 H0 : 모든 (alpha beta)ij = 0 -> 교호작용 없다

 vs H1 : 적어도 (alpha beta)ij 중 하나는 0이 아니다 -> 교호작용이 존재

이원배치 분산 분석

이원배치 분산 분석표

이원배치 분산 분석에서 가설검정

1. 인자 A에 대한 가설검정

- 검통 통계량 F0 = MSA / MSE > F(a -1, ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각

 즉, 인자 A가 반응치에 유의한 영향을 준다.

2. 인자 B에 대한 가설검정

- 검통 통계량 F0 = MSB / MSE > F(b -1, ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각

 즉, 인자 B가 반응치에 유의한 영향을 준다.

3. 교호작용 AxB에 대한 가설검정

- 검통 통계량 F0 = MSAxB / MSE > F( (a-1)(b-1), ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각

 즉, 인자 A와 B 사이에 교호작용이 존재한다.

이원배치 분산분석 예제

- 4종류의 사료와 3종류의 돼지 품종이 체중 증가에 미치는 영향

R에서 예제 실습

- 사료와 품종별 boxplot

- 품종별 boxplot 상에서

품종간에 큰 차이는 없어보임

사료별 boxplot

- 사료별 큰 무게 분포를 보인다.

분산분석

- 사료에 대한 유의확률 p val 0.00223로 매우 작음. 귀무가설 기각

 => 사료가 몸무게 증가에 유의한 영향을 준다.

- 나머지의 경우 유의확률이 크므로 귀무가설 채택.

유의확률 = 한계유의수준 = p value

유의수준 = alpha

일원 배치의 구조 모형

- 독립 변수(중요한 요인, 인자)가 하나. 이 변수가 종속 변수(반응치)에 어떤 영향을 미치는가?

1. 모수 인자(고정 인자)

- 관심 대상이 되는 반응온도에서 80도, 100도, 120도를 고정된 인자.

- 최적 조건

- 인자의 수준에 따라 반응치의 모평균이 바뀌는가

2.변량인자 (랜담인자)

- 80~120도사이 같은 구간 반응 온도는 변량 인자

일원 배치법의 구조 모형

오차 epsilon_ij에 대한 가정

- 정규성, 독립성, 불편성, 등분산성

분산분석

귀무가설 H0 : alpha1 = . . . = alpha_a = 0 

   => 수준 효과간 차이가 없다

   ex. 100도 = 120도 = 130도 .. 에서 차이가 없다.

대립가설 H1 : alpha_i 모두 0은 아니다

  => 어떤 수준에서 효과 간 차이가 있다.

변동에 대하여

분산 분석표와 가설 검정 방법

- 검정 통계량 F0 > F(a - 1, a(r-1) ; alpha)이면 유의수준 alpha에서 귀무가설 기각

- 유의확률 p val < 유의수준 alpha이면 대립가설 채택

일원배치 분산분석 예제 - 납품업체간 직물의 마모도에 유의한 차이여부

- 분산분석표

- 일원 배치 분산분석 결과

 검정 통계량 F0 8.78 > F(3, 12; 0.01) = 5.95

 => 귀무가설 기각

납품업체들 간에 직물 마모도 차이가 존재한다.

R로 일원배치 분산분석 실습

- 한계유의수준(유의확률, p val)이 0.00227로 유의수준 0.05보다 작다 => 귀무가설 기각

 업체들간 직물 마모도에 차이가 존재한다.(대립가설 채택)