





'수학 > 통계' 카테고리의 다른 글
| 파이썬R - 3. R데이터처리, dplyr (0) | 2020.10.28 |
|---|---|
| 파이썬R - 2. R 데이터처리 (0) | 2020.10.27 |
| 통계 - 16. 실험계획법과 검정 (0) | 2020.10.27 |
| 통계 - 15. 표본 분포와 가설검정 (0) | 2020.10.27 |
| 통계 - 14. 구간추정 (0) | 2020.10.27 |






| 파이썬R - 3. R데이터처리, dplyr (0) | 2020.10.28 |
|---|---|
| 파이썬R - 2. R 데이터처리 (0) | 2020.10.27 |
| 통계 - 16. 실험계획법과 검정 (0) | 2020.10.27 |
| 통계 - 15. 표본 분포와 가설검정 (0) | 2020.10.27 |
| 통계 - 14. 구간추정 (0) | 2020.10.27 |
용어
- 요인 factor : 결과값의 산포에 영향을 주는 원인들 중 실험에서 직접 취급되는 원인
- 반응 response : 실험의 결과로 얻어지는 양적자료
- 수준 level : 실험을 하기 위한 요인의 속성
- 처리 treatement : 요인의 수준 혹은 요인 수준의 좋바
- 실험 단위 experimental unit EU : 처리받는 대상, 다른 처리가 가해지는 최소 단위
- 관측 단위 Observational unit OU
일원 배치법 One-way ANOVA
- 고려하는 요인이 하나인 경우로 완전 랜덤화 설게를 전제로함
- 각 처리에 대한 데이터들은 정규분포를 따르는것을 가정
- mu_i = i번쨰 처리의 모평균
- 공통분산 sigma2를 가정
- 균형자료(등반복실험)을 가정
- 데이터 구조 => i번째 처리에서 j번째 반복을 함

- 모형

- 가설

- 분산분석표

- 총변동 등 정리

MS 제곱평균 Mean Square

완전 랜덤화 설계 CRD Completely Randomized Design
- N = rt 개의 EU를 사용하여 t개의 처리 비교
이원배치법
- 고려하는 변수가 2가지 있을떄.
범주형 자료분석
적합도 검정 goodness of fit test
- 관측 결과가 가설에 의해 주어진 확률분포를 잘 따르는지 확인하는 검정방법
=> 관측 도수의 기대도수에 대한 적합성여부 판정
- 가설
H0 : 관측 도수는 기대 도수를 잘 따른다.
H1 : 관측 도수는 기대 도수를 잘 따르지 않는다.
- 검정 통계량

1. 범주형 자료분석 (독립성 검정)
- 범주형 대 범주형
- 귀무 가설 h0 : 두 범주형 변수간 차이 x, 관계 x, 영향 x
- 대립가설 h1 : 두 범주형 변수간 차이 o, 관계 o, 영향 o
=> 우리는 두 변수간에 관계, 영향이 있는지 알고싶기 때문
2. 분산 분석
- 범주형 vs 연속형
- 귀무가설 h0 : 범주형 변수의 수준별로 연속형 변수의 평균이 같다. 동일하다.
- 대립가설 H1 : 범주형 변수의 수준별로 연속형 변수의 평균이 같지 않다.차이가 있다.
3. 상관 분석
- 연속형 vs 연속형
- H0 : 두 변수는 관계가 없다. 독립이다.
- H1 : 두 변수는 관계가 있다. 의존이다.
4. 회귀 분석
- 연속형 vs 연속형
- 상관 분석과 차이점은 X, Y가 존재하여 X가 Y에 영향을 주느냐가 중요
- H0 : 독립변수가 종속변수에 영향을 미치지 않는다.
- H1 : 독립변수가 종속변수에 영향을 미친다.
| 파이썬R - 2. R 데이터처리 (0) | 2020.10.27 |
|---|---|
| 파이썬R - 1. 파이썬 pandas (0) | 2020.10.27 |
| 통계 - 15. 표본 분포와 가설검정 (0) | 2020.10.27 |
| 통계 - 14. 구간추정 (0) | 2020.10.27 |
| 통계 - 13. 통계적 가설 검정 2 (0) | 2020.10.26 |
표본 분포
- 임의 현상에 대한 추론을 위해 모집단 population을 설정하는것은 통계분석에서 중요
-> 구성 원소 sampling unit 전체를 조사 census 하는것은 불가능
확률 분포 random sample
- 모집단의 각 구성원이 고르개 추출한 표본
- 특정한 확률 분포를 따르는모집단으로부터 독립적으로 관측(추출)된 표본
통계량 statistics
- 관측 가능한 확률 표본에 댛나 함수
- 확률 변수들을 대입하는 함수로, 통계량 또한 확률 변수가 된다.
-> 통계량의 확률 분포 : 표본 분포 sample distribution
- 모수는 관측하지 못하므로 모수는 통계량은 아님
- 표본의 함수인 통계량을 이용하여 통계적 추론을 수행
ex. 표본평균과 표본 표준 편차
검정 통계량 test statistic, T0 T(X)
- 모수에 대한 가설 검정에서 사용하는 통계량
중심극한정리 central limit theorem
- 평균이 mu, 분산 sigma2인 모집단으로부터 n개의 확률표본 추출시 n이 충분히 큰 경우
-> 표본 평균은 모집단 분포에 상관없이 평균mu, 분산 sigma2/n인 정규분포에 근사

통계적 검정 오류
- alpha 가 더 중요 하므로 1종 오류를 어느정도 줄인뒤 2종오류를 최소화함

예시
- H0 : 약품에 효과가 없다
=> 1종 오류 : 약품에 효과가 없지만 있다고 결론
- H1 : 약품의 효과가 있다.
=> 2종 오류 : 약품의 효과가 있지만 없다고 결론
위 경우 1종 오류가 더 크게 위험
유의 수준 significance level : alpha
- H0이 사실일떄, 이를 기각하는 제1종오류를 범할 확률
- 유의수준은 연구자가 상황에맞게 설정. 0.1, 0.05(흔하게), 0.01 등 주로 사용
기각역 ciritical region, reject region : C, Calpha
- 유의수준 alpha 하에서 귀무가설 H0을 기각하는 검정통계량의 값의 범위
=> 귀무가설을 기각하는 영역
유의 확률 p value
- 귀무가설을 기각할수 있는 최소 유의수준 = 귀무가설의 타당성정도
- 유의 확율이 크다면 타당성도 크다 =-> 채택
- 유의확률이 작다면 타당성이 낮아서 귀무가설 기각
가설검정의 의사걸졍방법
1. 검정통계량과 기각역 비교
-> 귀무가설하에서 검정통계량의 값이 기각역에 속하는가?
: T0 가 C_alpha에 속하면 H0를 기각

2. 유의수준과 유의확률 비교
: p-value < alpha이면 H0 기각
가설 검정 절차
1. 가설 설정 : H0, H1
2. 유의수준 설정 : alpha
3. 표본 관측 : X1, ..., Xn
4. 검정 통계량 선정 및 귀무가설 하에서 계산 : T0
5. 유의수준 alpha인 기각역 설정 : C_alpha
6. 의사결정 : T0가 C_alpha에 속하면 귀무가설을 기각, 아니면 채택
가설 검정하기 - 평균 검정
- X1, ..., Xn이 N(mu, sigma2)를 따를때

* iid : 독립, 동일 분포 independently identicaly distributed (즉, 표본을 의미)
- 귀무가설 H0 : mu = mu0 vs
- 대립가설 H1 : mu > mu0(우측단측가설/검정)
H1 : mu < mu0(좌측단척가설/검정)
H1: mu != mu(양측 가설/검정)
- 분산 sigma2가 알려진 경우
H0하에서 검정통계량

- 기각역
1) H1 : mu > mu0, Calpha = {T0 > Z_alpha} => T0 > z_alpha 이면 H0 기각
=> 대립가설 mu > m0이면 기각역은 T0> Z_alpha. 검정통계량 T0가 z_alpha이면 기각역에속함 귀무가설 H0기각
2) H1 : mu < mu0, Calpha = {T0 < Z_alpha} => T0 < z_alpha 이면 H0 기각
3) H1 : mu != mu0, Calpha = {T0 > z_alpha/2 or T0 < z_alpha/2}
=> T0 > z_alpha/2 or T0 < z_alpha/2 이면 H0를 기각
가설 검정 -평균 검정 2
- 분산 sigma2가 알려지지 않는 경우
- H0하에서 검정 통계량은

- 기각역
1. H1 : mu > mu0, T0 > t(alpha, n - 1)이면 H0 기각
2. H1 : mu < mu0, T0 < t(alpha, n - 1)이면 H0 기각
3. H1 : mu != mu0, |T0| > t(a/2, n-1)이면 H0를 기각.
상관 분석
- 분석에 사용될 변수들이 연속적인 값이며, 이들 간 관련성 확인하는 분석
ex. 키와 몸무게 관련성, 상품 광고액과 매출액 관계
- 두 변수의 산점도 이용(2차원 평면상 관측값 표기)
- 상관계수 사용(두 변수간 관계에 대한 수학적 정의)
분석의 종류
- 상관 분석 : 상관 관계 를 다룸-> 두변수간에 상관관계가 있는가
- 회귀 분석 : 인과 관계를 다름 -> x가 y에 영향을 미치는가...
- 범주형 분석
상관계수 correlation coefficient, rho
- 두 변수사이 선형 관계가 얼마나 강한지 나타냄
- 상관 계수의 정의
corr(x,y) = cov(x,y)/sqrt(var(x)) sqrt(var(y))
- -1 ~ 1의 값.
=> 1일 수록 양의 선형, -1일수록 음의 선형 관계, 0인 경우 무상관관계
회귀분석
- 독립 변수 : 조절할 수 있는 변수로, 원인이자 입력
- 종속 변수 : 독립변수에 영향을 받음, 결과이자 출력
- 종속 변수와 독립 변수 사이 (선형) 함수 관계를 회귀모형으로 구하고, 이에 대한 통계적 분석
=> 회귀분석 : 회귀 모형에대한 통계적 분석
회귀 분석에서 변수 설정의 중요성
- 회귀분석에서 가장 중요한것은 독립변수와 종속변수가 바뀌어선 안됨!!
=> 결과가 완전히 달라지므로 변수를 잘 설정해야함
- 범죄율과 경찰관의 수
- 경찰관(독립변수), 범죄율(종속변수)로 설정
-> 경찰관이 늘어날수록 범죄율이 늘어났다..로 잘못 해석
회귀 분석의 종류
- 선형 linear, 비선형 nonlinear : 함수 관계 형태
- 단순 simple, 중 multiple 회귀분석 : 독립변수(설명 변수)의 갯수
- 일변량 univariate, 다변량 multivariate 회귀변수 : 종속변수(반응 변수)의 개수
회귀 모형 regression model
- 종속변수 Y와 독립변수 X1, ..., Xp 사이의 관괴를 (비)선형 함수로 표헌하는것
- 변수로 독립변수와 종속변수
- 아래와 같은 형태

회귀 분석의 4가지 가정
1. 선형성
2. 독립성
3. 등분산성
4. 정규성
회귀 모형 추정하기 - LSM Least Squared Method 최소제곱법
- hat{y_i}와 yi에 최대한 가까운 b_k*를 찾음

- 잔차 residual를 최소화 하는 b_k* 찾아야함.

- 잔차들의 제곱합 sum of the squared residuals, SSE

=> SSE를 최소로 하는 b_k들을 구함.
회귀 모형의 적합도
- 독립변수가 종속변수를 얼마나 잘 나타내는가. 관측값의 평균에 대한 변동성 이용
- 총 제곱합 : 관측값들의 총 변동성(SST)

- 잔차 제곱합 : 적합된 값들의 총 변동성(SSR; residual sum of squares). 설명 안된 변동 residual ss

- 오차 제곱합 : 적합안된 값들의 총 변동성(SSE; explained sum of sqaured) 설명된 변동 model ss


자유도 df degree of freedom
- 정해지지않은 데이터 수.

결정 계수 coefficient of determinant
- 총 변동 SST 중에서 회귀 모형에서 설명되는 변동 SSR의 비율을 나타낸 것
- 0 ~ 1사이 값을 가짐
- 1에 가까울수록 관측값이 회귀선 주위에 밀집되며, 추정된 회귀모형이 관측값을 잘 설명

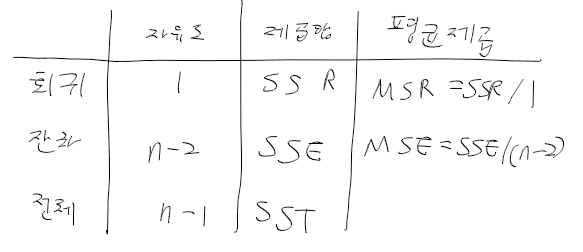
분산 분석
- 총 변동을 분해하여 모형에 의한 변동과 모형 이외의 변동 비를 확인하는것
- 각 변동을 각각의 자유도로 나누어주면 분산형태가 됨
- 이를 토대로 회귀모형 적합도에 대한 가설검정 수행
=> 회귀 분석의 적합도 기준이 됨
| 파이썬R - 1. 파이썬 pandas (0) | 2020.10.27 |
|---|---|
| 통계 - 16. 실험계획법과 검정 (0) | 2020.10.27 |
| 통계 - 14. 구간추정 (0) | 2020.10.27 |
| 통계 - 13. 통계적 가설 검정 2 (0) | 2020.10.26 |
| 통계 - 12. 통계적 추정 1 (0) | 2020.10.26 |
점추정에서는 모수의 한 값만을 추정하였다면
모수만 아니라 모수를 포함하는 구간 또한 추정이 가능함
-> 모평균, 모분산 구간추정방법
점 추정 point estimation
- 모집단이 정규분포를 따를때 모평균 mu에 대한 추정시
- mu의 최대가능도 추정량은 표본 평균과 동일하다

=> 주어진 자료로 모수 추정값 획득.
예제
- 다음 5개 데이터가 주어질떄 모평균 추정량을 구하자
- 10, 15, 5, 10, 15
-> 표본이 작을때 표본에 따라 모평균 추정량이 크게 바뀜

구간 추정 interval estimation
- 모수를 포함할 것으로 기대되는 구간을 제시하여 모수 추정

신뢰 구간 confidence interval
- 95% 신뢰구간 : theata에 대한 95% 신뢰구간을 구하는 과정을 100번 반복시, 100개의 신뢰 구간 중 95개가 모수포함

신뢰구간 예시
- sigma = 2, 최대가능도 추정량 theta = 15인 경우, 모수 theta에 대한 95% 신뢰구간은 아래와 같다.

신뢰 수준
- 신뢰구간을 구하는 과정을 반복 시, 모수를 포함하는 신뢰 구간의 비율의 극한
정규 모집단에서 모평균에 대한 구간 추정
- X1, ..., Xn ~ N(mu, sigma2), sigma2을 알때

정규 모집단 모평균에서 구간 추정 2
- X1, ..., Xn ~ N(mu, sigma2), sigma2을 모를때(t분포)

정규분포를 따른는 모집단에서 모평균 mu에 대한 신뢰구간 추정하기
- X1, ..., X16 ~ N(mu, sigma2) 이고

- sigma가 10, 모평균에 대한 95%신뢰구간

- 모표준편차가 알려져있지 않을때, 모평균에 대한 95% 신뢰구간 구하기

일반 모집단 모평균에 대한 구간 추정하기
- X1, ... Xn이 주어질때 모평균은 mu, 분산은 sigma2, sigma2는 미지
- 아래는 근사적으로 표준정규분포를 따름
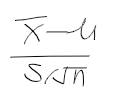
- mu에 대한 100(1-alpha)% 신뢰구간

일반 모집단 모평균에 대한 구간 추정 예제
- X1, .., X100 의 확률 표본이 주어지고 아래의 경우

- 모평균에 대한 95%신뢰구간

모분산에 대한 구간 추정
- 모집단이 N(mu, sigma2)를 따르는 경우, sigma2는 표본분산 S2로 구하기 가능.
- 확률 표본 X1, ..., Xn의 모집단이 위와같은경우 표본 분산의 확률 분포는 다음과 같음.

모분산 구간추정 예제
- 모집단이 정규분포를 따르고, 표본크기가 10, 표본분포 S2 = 9.8인경우 sigma2에 대한 95%신뢰구간

구간추정 interval estimation과 가설검정 hypothesis tset 사이 관계
- 유의수준 alpha에서 가설 H0 : mu = mu0 기각 못하는 범위

=> 모평균 100(1-alpha)% 신뢰구간과 일치
- mu 신뢰구간 = {mu | H0 : mu = mu0 기각하지 못함}
100(1-alpha) % 신뢰구간
- 유의수준 alpha에서 H0 : theta = theta0에 대한 채택역 A(theta0)
* 채택역 acceptance region : 귀무 가설을 기각하지 못하는 관측값의 영역

- 유의수준 alpha에서 채택역 A(theta0)일때 다음 식 성립

- theta에 대한 100(1-alpha)% 신뢰구간 이며, 주어진 X에 대해 모수의 집합 C(X)는 다음과 같다.

| 통계 - 16. 실험계획법과 검정 (0) | 2020.10.27 |
|---|---|
| 통계 - 15. 표본 분포와 가설검정 (0) | 2020.10.27 |
| 통계 - 13. 통계적 가설 검정 2 (0) | 2020.10.26 |
| 통계 - 12. 통계적 추정 1 (0) | 2020.10.26 |
| 통계 - 11. 통계적 가설 검정 (0) | 2020.10.26 |
가능도비검정. 최강력검정을 확장, 일반화
분할표를 이용하는 카이제곱검정
유의성 검정
최강력 검정
- 단순 가설이 존재

- 최강력 검정의 기각역 (R)

복합 가설에서의 가설검정
- 복합 가설하의 확률 밀도함수가 하나로 결정할 수 없음
-> 확률밀도함수 비를 바탕으로 최강력 검정 사용에 제약
- 하나로 결정되지 않는 확률 밀도함수 대신 각 가설하의 최대가능도를 이용

최대 가능도비
- 귀무가설 하 theta의 최대가능도 추정량 hat theta0

- 대립가설 하 theta의 최대가능도 추정량 hat theta1

가능도비 검정 likelihood ratio test
- 귀무 가설하 최대가능도와 모수 전체에서 구한 최대가능도의 비에 의해 기각역이 정해지는 검정
- 최대가능도비를 사용한 기각역 R (k' <1)

- 상수 k' : 주어진 유의수준 alpha에 따라 결정
- 다시 정리하면. 귀무 가설 (H0: theta가 omega0에 속한다) 하 최대가능도와
모수 전체(omega = omega0 합집합 omega1)의 최대 가능도의 비에 의해 기각역이 정해지는 검정

가능도비 검정 예제
- X1, ..., Xn ~ N(theta, 1)의 확률 표본
- H0: theta = theta0 vs H1: theta != theta0에 대한 유의수준 alpha에서 가능도비 검정을 구하자

가능도비 검정의 기각역
- 귀무가설이 참일떄 가능도비의 로그변환된 식의 근사적 분포는 카이제곱 분포를 따른다.

- 자유도 d.f : (모수 전체 영역에서 추정하는 모수의 수) - (귀무가설이 참인 영역에서 추정하는 모수의 수)
분할표 검정 contingency table test
- m개의 범주에서 빈도수를 N1, .... , Nm
- 각 범주에 속할 확률을 P1, ..., Pm

- 전체 빈도수를 n이라 할때 빈도수는 다항분포를 따름. 확률질량 함수는 다음과 같다.
* 이항분포가 2개중 1개를 선택한다면 다항분포는 m개중 1개를 선택

- 귀무가설과 대립 가설이 다음과 같을때

- 모수 전체 영역에서 pi의 최대가능도 추정량은 다음과 같다.

- 가능도비

- 유의수준 alpha 가능도비 검정의 기각역

- 테일러 급수를 이용한 근사

카이제곱 검정
- 다음의 귀무가설과 대립가설이 주어질떄

- 테일러 급수 근사한 유의수준 alpha 에서 가능도비검정의 기각역은 다음과 같다.

- 이 검정을 칼 피어슨이 처음 제안하여, 피어슨의 카이제곱 검정.
- 이것을 이용하여 적합도 검정, 독립성 검정 수행.
통계적 가설검정 이야기
- 피셔의 유의성 검정 : 귀무가설에 대하여 p 값 이용
- 네이만과 피어슨의 가설검정 : 귀무가설과 대립가설에 있어서 1종 오류를 발생시킬 확률과 2종 오류를 발생시킬 확률에 기반한 방법
피셔의 유의성 검정
- p value : 귀무가설 하에 주어진 관측값보다 극단적인 값을 얻을 확률 -> 귀무가설에 반대되는 근거
- 귀무 가설만 설정, 주어진 관측값에 이 가설이 부합하는지 알아봄.
=> 네이만과 피어슨이 피셔의 검정을 개선함
네이만과 피어슨의 검정 방법
- 귀무가설과 대립가설 설정
-> 1종 오류 확률 alpha, 2종오류 확률 beta, 검정력
- 주어진 alpha에 대해 대립가설을 고려하여 최적의 기각역을 구함.
| 통계 - 15. 표본 분포와 가설검정 (0) | 2020.10.27 |
|---|---|
| 통계 - 14. 구간추정 (0) | 2020.10.27 |
| 통계 - 12. 통계적 추정 1 (0) | 2020.10.26 |
| 통계 - 11. 통계적 가설 검정 (0) | 2020.10.26 |
| 통계 - 10. 점추정량 비교2 (0) | 2020.10.26 |
용어
- 추정 : 표본으로부터 모집단에 대한 값을 구해나가는 것
- 추정량 : 모수를 추정하기위한 표본의 함수
- 모수 : 모집단에 대한 특성을 나타내는 값
- 점 추정 : 모수에 대한 추정
- 구간 추정 : 점 추정 + 정확도 추정
- 신뢰 수준 : 모수의 참값이 속할것으로 기대되는 구간안에 모수가 포함될 가능성 확률
통계적 추론
- 우리 주위에 대한 데이터 수집, 요약
- 수집한 데이터로부터 일반성을 찾음
- 불확실한 사실에 대한 결론, 예측
기술 통계학 descriptive statistics
- 데이터의 특성들을 요약, 정리
(표본 평균, 표본 분산 등)
- 판단하기 힘듬
통계적 추론 구조
- 모집단 : 알고자 하는 관측 대상 -> 모든 관측값의 집합. 전체다 알기 힘듬
- 표본 : 모집단의 일부 -> 모집단에서 임의추출하여(모집단을 잘 대표하도록) 모집단을 추측한다.
- 모집단의 변수들은 어느 확률 분포를 따름
- 확률 분포 : 몇개의 모수(평균, 분산, 첨도, 왜도, 람다 등)으로 구성된 수리적 함수
-> 이항 분포, 정규 분포 등
모집단의 파악
- 정규 분포의 모수 : 모 평균과 모분산
- 이항분포의 모수 : 모비율
- 카이제곱 분포, t분포는 자유도에 의해 결정
통계적 추론 구조
- 통계량 : 표본의 함수 -> 모수를 추정
-> 표본 평균, 표본 비율, 표본 분산 등
- 추정량 : 모수를 추정하는데 사용되는 통계량
- 추정값 : 관측된 데이터를 추정량(통계량)에 대입하여 얻은 값
추정량의 분포
- 추정량은 추출한 표본들에 따라 변화하게 됨
=> 표본 분포 sampling distribution
* 표본 분포는 추출한 샘플들에 따라 달라짐
여론조사의 분포?
- 표본들이 매번 바뀌기 때문에 표본 분포는 다름
추정과 검정
- 추정 : 표본으로부터 모집단에 대한 정보인 모수를 추측함.
- 검정 : 모집단과 관련된 주장에 대한 타당성을 표본으로 점검
-> 표본으로 얻은 증거가 우연인지 아닌지 점검
추정
- 점추정 : 모수에 대한 하나의 추정값을 구함
- 구간 추정 : 모수에 대한 추정값과 정확도를 구함
ex. 3% +- 1%
- 모수 theta에 대해 두 통계량 (L, U) : theta의 (1-alpha) x 100% 신뢰구간
P(L < theta< U) = 1 - alpha
* Lower bound 하한, Upper bound 상한
적합한 추정량
- 불편성, 일치성, 효율성
- 불편향성 : 가능한 모든 통계값의 평균이 모수가 됨
-> 표본 평균은 모평균의 불편향 추정량
- 일치성 : 표본 크기가 커질수록 추정량의 값과 모수가 더 가까워짐
-> 표본 평균의 분산은 표본크기가 커지면 0, 표본 평균은 모평균에 근점
- 효율성 : 추정량중 분산이 작은것을 의미
바람직한 추정량을 구하는 방법
- 최대가능도 추정법
- 적률 추정법
- 최소제곱 추정법
최대 가능도 추정법
- 미지의 모수를 가지는 모집단의 분포에서 확률 표본을 추출하여 추정량찾음
- 표본의 몯느 정보는 결합확률밀도함수인 가능도 함수에 있으므로 최대 가능도 추정법으로 찾음
| 통계 - 14. 구간추정 (0) | 2020.10.27 |
|---|---|
| 통계 - 13. 통계적 가설 검정 2 (0) | 2020.10.26 |
| 통계 - 11. 통계적 가설 검정 (0) | 2020.10.26 |
| 통계 - 10. 점추정량 비교2 (0) | 2020.10.26 |
| 통계 - 9. 복습? (0) | 2020.10.26 |
피셔의 밀크티 실험
- 주장 : 우유에 차를 넣은 홍차와 차에 우유를 넣은 홍차의 맛을 감별할 수 있다.
- 전체 8개의 잔 중에서 차를 먼저 넣은 잔이 4잔이 있음.
- a는 홍차를 먼저 넣었다고 올바르게 판단한 잔의 수. a는 0~4 중 한가지 값.

- 해당 주장이 근거가 없다는 가정하에 여덟 잔중에 먼저 4잔을 찾아낼 확률

- 차를 넣은 네 잔을 정확히 찾을 확률을 1/70으로 매우 작음.
=> 통계적인 관점에서도 주장이 틀렷다고 말하기는 힘들다
- 정확히 4잔을 찾기도 힘듦으로
밀크티 실험 가설
- 가설 1 : 차와 우유 둘 중 무엇을 먼저 넣었는지 알수 있다.
- 가설 2 : 차와 우유 둘 중 무엇을 먼저 넣었는지 알 수 없다.
가설 검정 개요
- 통계적 가설검정 : 확률 표본으로 모집단의 배반적인 두 가설중 무엇이 타당한지 판단
- 대립가설 H1 : 입증하려는 가설
- 귀무가설 H0 : 대립가설에 반대되는 가설
통계적 가설검정
- 실험을 통해 얻은 자료, 데이터로 어느 가설이 타당한지 판단하는 것.
- 귀무 가설이 참이라는 가정 하에 주어진 관측값보다 더 벗어난 값을 얻을 확률이 작다면
-> 귀무 가설이 참이라는 가정은 올바르지 않다고 판단.
가설 검정 hypothesis testing 의 개요
- p-값 : 귀무 가설 하에서 주어진 관측값보다 더 극단적인 값을 얻을 확률
-> p값이 작다는 것의 의미 : 귀무가설이 참이 아니거나 귀무가설이 참이라면 매우 희귀한 사건이 발생
- 기각역 R : 귀무가설을 기각하는 관측값의 영역
-> 관측값이 기각역 R에 속하면 귀무가설 기각
-> 관측값이 기각역에 속하지 않으면 귀무가설을 기각할수없음
검정 오류
- 제 1종 오류 alpha : 귀무가설이 참이라는 하에서 기각하는 확률
- 제 2종 오류 beta : 대립가설이 참이라는 가정하에서 기각하지 못하는 확률

- 검정력 : 대립가설이 참일때 귀무가설을 기각할 확률

검정력 예제
- 다음의 조건 하에 제1 종 오류, 제 2종 오류를 범할 확률, 검정력을 구해보자

- 제 1종 오류 alpha : 귀무 가설이 참이라는 가정 하여 기각하는 확률

- 제 2종 오류 beta : 대립 가설이 참이라는 가정하에 기각하지 않을 확률

- 검정력 power : 대립가설이 참일때 귀무 가설을 기각할 확률로 1 - beta

검정
- 기각역 R에 의해 결정
- R = {x | x>=c}, 제 1종 오류와 제 2종 오류
-> c의 값에 따라 alpha가 커지고 beta가 작아지거나. 반대의 현상이 나타날 수 있음
검사 특성 곡성 operating characteristic curve
- 제 1종 오류를 작게하면 검정력이 작아짐(제 2종 오류가 커짐)
-> 제 1종 오류 alpha를 x축, 검정력 power를 y축에 둔 그래프
- 오류의 상충 : 제 1종 오류를 범활 확률을 작게하는 검정은 제 2종 오류 확률을 높임
검정의 선택
- 제 1종 오류 범확 확류이 일정 수준 이하인 검정 중 제 2 오류 범할 확률을 가장 작게하는 검정 선택
- 유의 수준 : 제1 오류를 범할 확률의 최대 한계
- 수준 alpha 검정 : 제 1종 오류를 범활 확률이 alpha이하인 검정
검정 함수

검정 함수 일반화
- 연속형에서는 괜찬으나 이산형인경우 검정 함수가 5%에 딱맞는 유의수준이 존재하지 않을수있음.
- delta(x) = 1 : 귀무가설 기각
- delta(x) = 0 : 귀무가설 기각 x
- delta(x) = 1/2 : 귀무가설 기각확률 0.5
최강력 검정 개요
- UMVUE와 같은 개념으로 볼수 있음
- 단순 가설 simple hypothesis : 귀무가설이나 대립가설하에 X의 확률분포가 하나로 결정.
ex. H0: theta =1
- 복합 가설 composite hypothesis : 확률분포가 하나로 결정되지 않을때 가설
ex. H1: theta >1 , H1:theta != 1
귀무가설과 대립 가설이 모두 단순 가설인 경우
- 아래와 같이 표현 가능
H0: theta = theta0 vs H1: theta=theta1
최강력 검정 most powerful test
- 기각역이 R인 검정이 아래의 조건을 만족하는 경우 유의수준 alpha에서의 검정

=> 제 1종 오류를 범할 확률이 alpha 이하인 검정 중에서 제 2종 오류를 최소로 하는 검정
네이만-피어슨의 보조정리 neyman-pearson lemma
- 최강력 검정을 구하는 구체적인 방법

- 상수 k에 대해 주어지는 기각역 R이 P(X는 R의집합 | H0) = alpha일때,
기각역 R인 검정이 유의수준 alpha에서의 최강력 검정
- f(x |theta0), f(x|theta1)은 귀무가설과 대립가설이 참인 경우 확률 밀도 함수
가능도비 검정
- 최강력검정은 귀무가설과 대립가설이 모두 단순 가설인 경우 사용 가능
- 귀무가설, 대립가설이 복합가설인 경우 사용되는 검정으로 가능도비 검정
일단 통개학 개론을 모르고 바로 수리 통계학을 하다보니 어려움을 많어서 잠깐 여기서 멈추고
개론 부터다시 시작해야될듯 싶다.
| 통계 - 13. 통계적 가설 검정 2 (0) | 2020.10.26 |
|---|---|
| 통계 - 12. 통계적 추정 1 (0) | 2020.10.26 |
| 통계 - 10. 점추정량 비교2 (0) | 2020.10.26 |
| 통계 - 9. 복습? (0) | 2020.10.26 |
| 통계 - 8. 점추정량 비교 (0) | 2020.10.26 |
일치성
- 표본 크기가 증가할 수록 추정량의 분포가 모수로 수렴하는 성질

일치 추정량
- Tn = T(X1, ..., Xn) n개의 표본을 사용한 추정량
- {T1, ..., T_inf}는 모수 theta에 대한 점추정량 수열
- Tn을 일치 추정량이라 함.

충분성 sufficiency
- 모수에 대해 더이상 정보를 제공하는 통계량이 없는 경우.
=> 그 추정량은 충분성을 가짐
- 통계량이 표본 모수에 대한 정보를 읽지않고 모수를 추정할 수 있는 성질
- 충분통계량 : 충분성을 같는 통계량
충분 통계량
- theta에 대한 추정량 T에 대해 T가 주어졌을때 X1, X2, ..., Xn의 조건부 분포가 모수 theta에 의존하지 않을때 T
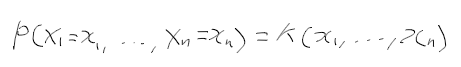
피셔-네이만 인수분해 정리
- 확률 표본 X1, ..., Xn에서 theta의 추정 통계량 T = h(X1, ..., Xn)이 충분 통계량일 필요 충분조건
=> 결합확률밀도함수가 함수 g와 h로 표현되는것.

충분 통계량 예제 1
- X1, ..., Xn이 정규분포 N(mu, 1)을 따르는 확률 표본인경우 mu에 대한 충분 통계량 구하기

완비 통계량 complete statistics
- 완비성을 갖는 통계량
- 통계량 함수의 기대값이 모든 모수에서 0인 경우 통계량 함수 값 자체가 0인 통계량
- 충분 통계량이면서 완비 통계량인경우 => 완비충분통계량(complete and sufficient statistic, CSS)
완비 통계량
- 모든 theta와 통계량 T(X)의 함수 g에 대해 아래가 성립하는경우 T(X)
- 모든 theta와 함수 g에 대해 다음이 성립 -> T(X)가 완비통계량

완비통계량 예제
- 확률 표본이 베르누이분포 Ber(P)를 따르는 경우, Sigma Xi가 p에 대한 완비통계량 증명

완비 통계량 복습

지수족 exponential family
- 확률 밀도/질량 함수가아래와 같은 형태인 경우
=> 쉽게 완비 충분 통계량을 구할 수 있다.

완비충분통계량 구하기
- X1, ..., Xn이 Poisson(lambda)를 따른는 경우. lambda의 완비충분통계량

- 확률 표본 X1, .. ,Xn이 N(0, sigma2). sigma2에 대한 완비충분통계량

Basu의 정리
- T(X)가 완비 충분 통계량이면 T(X)는 모든 보조 통계량에 독립적
좋은 추정량
- 모수 theta의 불편향 추정량 중 최소 분산인 추정량
- 불편향 추정량과 편향 추정량 등 추정량 중에서 평균 제곱 오차를 최소로 하는 추정량
균일 최소 분산 불편향 추정량 uniformly minimum variance unbiased estimator, UMVUE
- 불편향 추정량에 한정하여 찾은 추정량
- 균일최소분산불편추정량을 찾기 위해 이용되는 개념이 충분성과 완비성
=> 평균제곱오차의 최소값을 갖는 불편향 추정량

- 균일최소분산불편추정량을 구하는 방법 => 라오 블랙웰 정리
라오 블랙왤 정리

균일최소분산불편향추정량 예제
- X1, X2 가 Poisson(lambda)의 확률표본 lambda의 균일최소불편추정량

레만-쉐페의 정리
- 더 쉽게 UMVUE를 구할수 있음.

UMVUE 예제 2
- X1, .. Xn ~ Ber(p), p의 UMVUE는?

UMVUE 예제 3
- X1, .., Xn ~ N(mu,sigma2), mu,sigma2에 대한 UMVUE

크래머-라오 하한
- 모수 theta를 추정하는 2개의 불편향 추정량이 있는 경우, 추정량의 분산이 작은게 더좋을것임
- 최소 분산을 갖는. 그러니 가장 좋은 추정량이 되는걸 알아내는 방식으로 크래머-라오 하한 제안
크래머-라오 하한 cramer rao lower bound CRLB
- 어느 불편 추정량의 분산이 크래머-라오 하한과 동일하면 이 추정량은 UMVUE

| 통계 - 12. 통계적 추정 1 (0) | 2020.10.26 |
|---|---|
| 통계 - 11. 통계적 가설 검정 (0) | 2020.10.26 |
| 통계 - 9. 복습? (0) | 2020.10.26 |
| 통계 - 8. 점추정량 비교 (0) | 2020.10.26 |
| 통계 - 7. 점추정 (0) | 2020.10.25 |
확률 관련 기초 용어
- 확률 probability : 확률 변수가 특정한 값/구간에 속할 가능성으로 0 ~ 1의 값으로 표현
- 확률 실함 random experiment : 결과를 알수 있는 실험
- 시행 trial : 확률 실험을 수행하는 행위
- 원소 element : 시행의 결과
- 표본 공간 sample space : 모든 원소들의 집합
- 사건 event : 표본 공간의 부분집합으로 관심 대상(원소)로 구성
확률의 정의
- 빈도주의 정의 : 관심 사건 횟수/ 전체 실험의 횟수
=> P(A) = lim n(A)/n
- 주관주의 확률 : 믿음의 정도
확률 변수 random variable
- 확률 실험의 모든 가능한 결과에 일정한 규칙에 따라 특정 값을 부여한 것
- 표본 공간을 실수로 변환하는 함수
- 정의역이 표본공간, 치역이 실수인 함수
확률변수 예제
확률 변수 X ~ B(3, 1/2)
동전 던지기
앞면의 횟수 0 1 2 3
확률 1/8 3/8 3/8 1/8

복습
표본 분산의 확률 분포
- 대표적으로 카이제곱 분포와 t분포가 있음.
카이제곱분포
- 모분산 추정, 적합도 검정, 교차표 검정에 사용
- 감마 분포의 특수한 경우 r = n/2, lambda = 1/2인 경우 확률변수 X는
=> X ~ chi2(n)으로 표현
카이제곱 분포의 특성

표본분산 S2의 확률분포

t분포의 필요성
- 보통 모집단이 정규분포를 따르고, 확률변수들이 독립이면 아래와 같으나

- 보통 확률 표본을 추출한 경우 모집단의 분산을 알수 없음
=> 표본분산 S2를 구하고 sigma2대신 사용.
- 의문점 : S로 대채한 다음 통계량의 분포는 어떻게 될까?

t분포
- 위 통계량의 분포는 정규분포가 아니라 t분포를 따름
- t 통계량의 pdf를 구하려면 정규분포와 카이제곱분포를 사용해야함.

t분포의 확률밀도함수
- 변수 변환법으로 구하면

| 통계 - 11. 통계적 가설 검정 (0) | 2020.10.26 |
|---|---|
| 통계 - 10. 점추정량 비교2 (0) | 2020.10.26 |
| 통계 - 8. 점추정량 비교 (0) | 2020.10.26 |
| 통계 - 7. 점추정 (0) | 2020.10.25 |
| 통계 - 6. 표본분포 (0) | 2020.10.25 |
적률 추정량
최대 가능도 추정량
어떤 추정량이 좋은 추정량인가?
=> 불편 추정량, 추정량 효율성, 일치추정량, 평균제곱오차를 보자
추정량 estimator
- 모수를 추정하는데 사용되는 통계량 (표본의 함수, 표본평균/표본분산)
추정값 estimate
- 데이터에 근거한 추정량 값
좋은 추정량
- 추정량의 값이 모수와 항상 일치
- 추정량 선택 기준 : 불편성, 효율성, 일치성
추정량의 성질
- 불편성 : 평균하면 모수가 되는가
=> 불편 추정량 unbiased estimator : 불편성을 가진 통계량
- 효율성 : 얼마나 밀집되어있는가
- 일치성 : 수렴한느가

불편향추정량 unbiased estimator
- 통계량 T가 다음을 만족하면 T는 불편 추정량
=> 불편향 추정량 : E(T) = theta
=> 불편향 추정량의 기대값은 모수가 됨.
편향 추정량 biased estimator
- 불편향 추정량이 되지 못하는 추정량
=> 편의 : bias(T) = E(T) - theta

불편향추정량 예제
- X1, ..., Xn ~ Poisson(lambda)를 따르는 확률표본인 경우
- T1 = bar{X}이 불편추정량임을 증명

=> E(T1) = E(bar{X}) = lambda로 모수임을 증명함
편향 추정량 예제
- 다음 추정량의 편향을 구하라

효율성 efficiency
- 분산의 역수
- 불편 추정량 hat{theta}의 효율성

효율성 예제
- X1, ..., Xn ~ N(mu, sigma^2)을 따르는 확률 표본
- S2과 hat sigma2의 효율성을 구하라


-
상대 효율성 relative efficienty
- 하나의 모수를 추정하는 2개의 불편 추정량이 있다면, 그 성능은 효율성으로 비교
- 모수 theta에 대해 불편추정량 T1, T2가 있을떄 T1에 대한 T2의 상대효율성

평균제곱오차의 필요성
- 불편 추정량과 편의 추정량 비교를 하기 위해 아까 본 예제를 다시보면

- 편향성과 효율성을 동시에 고려해야하며 기준 필요
=> MSE
평균제곱오차 Mean Sqaure Error, MSE
- 추정량 T와 모수 theta간 거리 제곱의 평균 측정값
- 통계량 T가 추정 통계량인 경우 T에 대한 평균제곱 오차는 다음과 같다.

평균 제곱 오차의 정리
- 통계량 T에 대한 평균 제곱 오차를 편향과 분산으로 나누면 다음과 같다.

평균 제곱오차 예제
- X1, .., Xn이 N(mu, sigma2)를 따르는 확률 표본인경우 추정량의 효율성과 평균제곱오차를 구해보자
- S2의 효율성과 평균 제곱오차

- sigma2 추정량의 효율성과 평균제곱오차를 구해보자

| 통계 - 10. 점추정량 비교2 (0) | 2020.10.26 |
|---|---|
| 통계 - 9. 복습? (0) | 2020.10.26 |
| 통계 - 7. 점추정 (0) | 2020.10.25 |
| 통계 - 6. 표본분포 (0) | 2020.10.25 |
| 통계 - 5.표본분포 (0) | 2020.10.24 |