집밖은 위험해

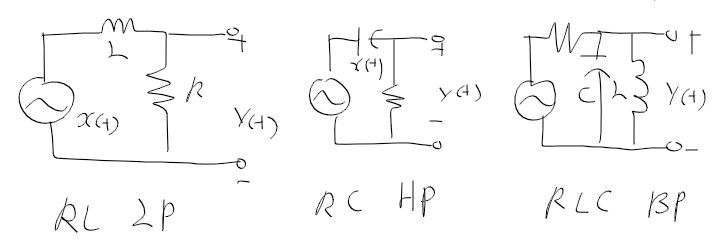
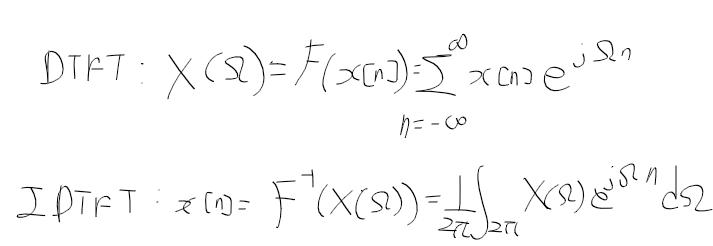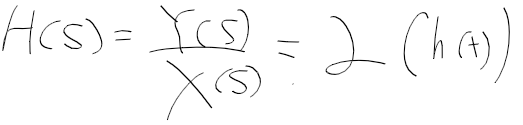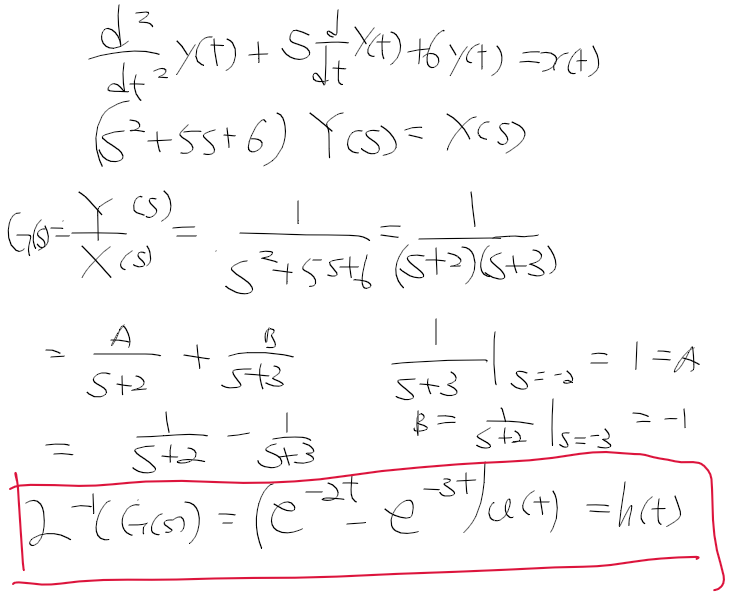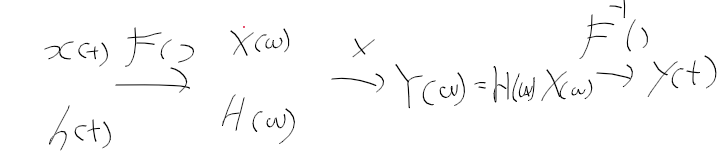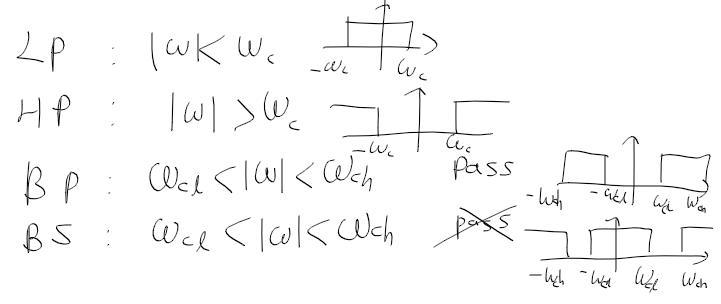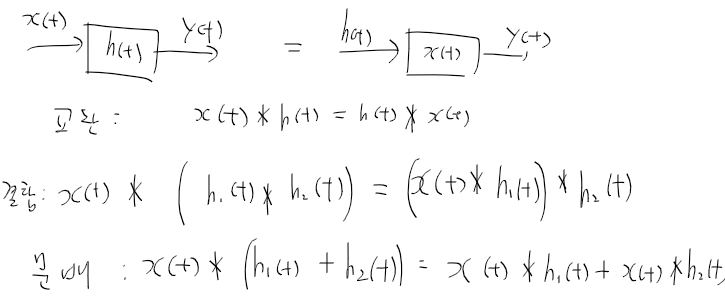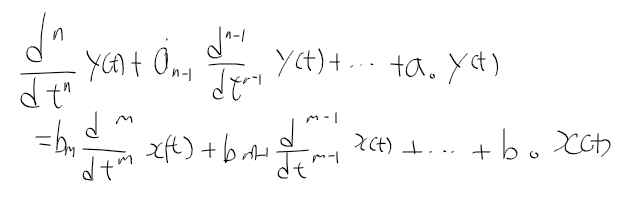BJT

- Bipolar Junction Transistor 양극 접합 트랜지스터

- npn, pnp 형 접합

- 다수캐리어 전자, 소수캐리어 정공

- 두 극성이 이용됨

* UJT

- Unifpolar Junction Transistor

- 단극성으로 다수 캐리어만 사용한 트랜지스터

- ex : FET

* Transistor

- Trans : 변화

- Resistor : 저항

- 전압이 일정해도 저항을 변화시켜 전류도 변화시킴

전력 트랜지스터

- 전자회로에서 1A는 크다.

- 1A 큰 전류/전압을 사용하는 곳에서 전력 트랜지스터 이용

 ex) 오디오에서 스피커로 음성 출력시 전력 트랜지스터 필요

-> 출력 전력이 클수록 열이 발생 -> 방열판 필요

RF 트랜지스터

- 수십 MHz 이상 주파수 신호를 처리시 사용

- 일반 트랜지스터와 동일하나 방열을 위한 다른 형태의 케이스 사용

바이어스

- 소자/장치 동작을 위해 인가하는 전압/전류

- 트랜지스터 동작을 위해선 동작 목작에 따라 적절한 바이어스가 필요

npn,pnp TR 동작 시 바이어스

- B-E : 순방향 바이어스

- B-C : 역방향 바이어스

Tr 동작 과정 (npn)

1. B-C 접합 사이 역방향 바이어스가 걸리면서 공핍층이 증가

2. B-E 접합 사이 순방향 바이어스가 걸리면 일부 전자들이 베이스의 정공과 결합하고, 일부는 컬렉터까지 넘어감

3. E의 전자들이 C까지 넘어가면서 전류 I_B와 I_C가 흐른다

라플라스 변환

- 푸리에 변환이 불가능한 비주기 발산 신호를 임의의 복소 지수함수  e^-st를 이용하여 감쇄해 s 영역으로의 변환

라플라스 변환의 예시

+ Z 변환(이산 시간에서의 라플라스변환) 예시

전달 함수

- 시불변 시스템 : 입출력이 시간의 변화에 영향을 받지 않는 시스템(미방의 경우 계수가 시간에 따라 변하지 않음)

- 전달 함수 : 시간 영역에 대한 함수를 라플라스 영역으로 변환한 후 출력/입력으로 나타낸 다항식

- 극점과 영점 : 전달함수 분모의 근을 극점, 분자의 근을 영점

- 응답들 : 임펄스 응답, 계단 응답, 특정 주파수 입력에 대한 주파수 응답

전달함수와 응답들

- 임펄스 응답 : 전달 함수에 임펄스 응답의 라플라스 변환을 곱한 후 역라플라스 변환으로 시간 영역으로 나온 결과

                       = 전달 함수의 역라플라스 변환

- 계단 응답 : 전달 함수에 계단 입력의 라플라스 변환을 곱한 후 역라플라스 변환으로 얻은 결과

- 목표 : 입력과 출력이 동일해 지도록, G(s) = 1 이 되도록 제어 시스템을 설계해야 한다.

물 탱크 채우기 시스템

- 가정 : 바닥 면적 C인 물탱크, 물이 qi(t) 만큼 들어오고, qo(t)만큼 나가며, 수면 높이는 h(t)이며 다음의 관계를 갖는다면

- qi(t) 가 1m^3 이라면 (= 계단 입력)

시스템과 제어

- 시스템 : 로봇, 차량, 기차 등과 같이 기계/전기 요소들로 구성된 것

- 제어 : 시스템이 원하는 동작을 하도록 조절하는 것

- 입력 : 제어 시스템이 행하기를 원하는 동작

- 출력 : 제어 시스템의 반응

- 이상적인 제어 시스템 : 입력 = 출력. 모델링하여 고려할수 없는 것들이 많으므로 현실적으로 불가능.

- 부시스템(제어기) : 실제 시스템에 가깝게 출력을 나오도록 보상해주는 시스템

- 설계 : 최고의 성능을 내도록 제어기를 만드는 것

- 시스템 이론 : 시스템을 시간과 주파수 영역에서 다루며 아래의 해석, 설계 도구를 이용

    - 시간 영역 : 임펄스/계단 응답, 루트 로커스 등

    - 주파수 영역 : 보드/나이퀴스트/니콜스 선도 등

피드백과 제어

- 일반적인 제어 시스템은 피드백의 형태

- 폐루프 시스템 : 피드백을 통해 입력과 출력 사이에 닫혀진 루프가 존재하는 시스템

- 개루프 시스템 : 피드백 없어 루프가 존재하지 않은 시스템

- 자동 제어 : 피드백을 통해 원하는 출력이 나오도록 자동적으로 조절하는 것

- 외란 : 사용자 입력 이외에 시스템의 출력에 영향을 주는 것

- 감도 : 출력이 변동에 영향 받는 정도 -> 피드백을 이용하여 완화 가능

- 안정성 : 환경 변화에도 대처하여 기존의 동작을 유지하는 정도

현대 제어 공학

- 컴퓨터를 활용해 고전적 기법인 보드/나이퀴스트/니콜스 선도와 루트 로커스 등을 쉽게 이용 가능

- 배, 우주선, 로봇 등 다방면으로 활용되고 있음.

제어 시스템 해석 및 해석

- 기본적으로 제어 시스템은 과도 상태를 피드백을 통해 완화하여 정상 상태가 된다.

 => 과도 응답, 정상 상태 응답을 통해 시스템 해석

- 과도 응답 : 정상 상태에 들어가기 전 시스템의 출력으로 시간 영역뿐만 아니라 주파수 영역으로 변환하여 해석 할 수 있다.

- 정상상태 응답 : 과도기를 지난 후 안정된 상태에서의 출력.

- 정상상태 오차 : 입력과 정상상태 응답 사이의 차이

- 안정성 : 시스템 극점의 위치에 의해 안정한지 불안정한지 결정된다.

- 시스템 설계 : 물리적인 것을 만든다기 보다는, 외란과 응답 등에 잘 대응하는 제어기를 설계하는 행위

기본 이산 신호

1. 단위 이산 임펄스 함수

- 연속 임펄스 함수 신호와는 달리 n = 0에서만 1인 값을 갖는 신호

2. 이산 계단 함수

- n >= 0 에서 항상 값이 1인 함수 = 직류 신호

- 단위 이산 임펄스 함수 = u[n] - u[n - 1]

3. 이산 지수함수

- a의 값에 따라 실수/복소/복소정현파 지수 함수로 나뉜다.

- 실수 지수함수 : a = 실수 인 경우

- 복소 지수함수 a가 복소수인 경우

- 복소 정현파 함수 : r = |a| = 1인 경우

디지털 신호의 생성과 샘플링

1. 샘플링 : 연속 신호로부터 일정 시간 간격마다의 값을 추출

2. 양자화 :  샘플링된 값을 일정 구간별로 나누는 과정

3. 부호화 : 디지털에서 해석 가능한 이진 부호화의 과정

- 샘플링 : 연속 신호로부터 일정 시간 간격마다 순시값을 얻어 이산 신호로 만드는 과정

대부분의 내용은 연속 신호 처리와 유사하니 간략하게 넘어간다.

이산 시간 푸리에 급수, 변환, z변환

- 푸리에 급수 : 직류 성분 기본파, 고조파 성분을 가진 이산 주기 신호를 급수 형태로 나타낸 것

- 이산 시간 푸리에 (역)변환 : 비주기 이산신호로부터 주파수 스펙트럼을 구하는 것

- z 변환 : DTFS에서 무한급수 합의 수렴성을 보장하기 위해 z의 함수로 나타낸 변환

주요 신호의 z 변환

푸리에 변환이 불가능한 경우

- 일부 신호의 경우 디리클레 조건을 만족하지 못해 푸리에 변환이 불가

- 입력 신호가 발산하지 못하게 더 빠르게 커지는 감쇠 지수함수를 곱하면 디리클레 조건을 만족 하여 적분이 가능해짐.

라플라스 변환

- 푸리에 변환에 감쇠 지수 함수를 추가하여 발산을 방지하면서 주파수 스펙트럼을 구하는 복소 주파수 s에 대한 변환

푸리에 급수, 변환, 라플라스 변환의 관계

초깃값/최종값 정리

- 초깃값 정리 : t=0 일때 x(t), 초깃값은 s = inf일때의 sX(s)와 같다

- 최종값 정리 : t=inf 일때 x(inf), 최종값은 s = 0일떄의 sX(s)와 같다.

라플라스 변환, 역변환 정리

라플라스 변환을 이용한 전기 회로 해석

- RLC 회로에서 직류 전압 x(t)을 가할 때 출력 전압 y(t) 

전달함수

- 주파수 영역에서 출력/입력이자 주파수 응답의 라플라스 변환

* 미분방정식 -> 전달함수 -> 역라플라스 변환 -> 임펄스 응답

대략 정리

- 지금까지 다양한 기본 신호와 시스템, 컨볼루션 연산 등을 살펴봄

- 신호는 연속 신호와 이산 신호로 구분 할 수 있으며, 주기 신호 여부에 따라 푸리에 급수, 푸리에 변환을 통해 해석.

- 이후 연속 신호는 라플라스 변환, 이산신호는 z 변환으로 해석하며, 신호는 주파수 스펙트럼, 시스템은 전달함수로 알아볼 예정

푸리에 변환

- 비주기 신호도 해석 하기 위해서 기존의 푸리에 급수에서 주기를 무한대로 늘려 해석

- 푸리에 급수의 경우 주기 신호인 만큼 주기가 셀수 있는 만큼 존재하였으나, 비주기 신호의 경우 다양한 주기의 신호들이 존재한다고 봄 => 연속적인 주파수 스펙트럼을 얻음으로서 적분으로 표현

푸리에 급수와 변환 의 관계와 조건

- 푸리에 변환은 모든 구간에서 디리클레 조건(적분 시 수렴 가능여부)을 만족해야함

 + 주기 신호를 푸리에 변환하는 경우? 주파수가 이산적이므로 이산함수가 된다.

주파수 응답

- 시간영역에서의 시스템 응답 : 콘볼루션 연산 혹은 미분 방정식 이용 -> 어려우며, 주파수 정보 부재

- 시스템을 주파수 변환하여 해석하는것이 좋음

 -> 주파수 특성 파악 용이, 시간 영역에서 콘볼루션은 주파수 영역에서는 곱 연산임. 미방의 경우 쉽게 결과 취득

- 주파수 응답 H = 주파수 영역에서의 Y/X

복소 정현파 입력에 대한 주파수 응답(콘볼루션 연산)

주파수 응답을 이용한 시간영역에서의 시스템 출력 구하기

1. 입력, 임펼스 응답 -> 푸리에 변환

2. 입력 스펙트럼과 시스템 주파수 응답 곱 연산 -> 출력 스펙트럼

3. 푸리에 역변환으로 시간 영역에 대한 출력 신호 구하기

주파수 응답 및 필터

- 주파수를 활용하기 좋은 분야로 필터가 있음.

- 주파수 선택 필터 : 필요한 성분만을 걸러내는 필터

  종류 : 저역 통과/고역 통과/대역 통과/대역 저지 필터

전기 회로를 이용한 필터

- RL 저역통과, RC 고역통과, RLC 대역 통과 필터

개요

- 그동안 살펴본 시간에 대한 함수를 주파수에 대한 함수로 변환하여 시스템을 해석하자

신호의 성분

- 신호는 기본 신호로 (주파수 벌로) 나눌 수 있음

 => 주파수에서 보면 분석하기 좋음

주파수 스펙트럼

- 주파수축 상에 정현파의 진폭과 위상을 표현한 것

 -> 진폭 스펙트럼과 위상 스펙트럼으로 나뉨

시간/주파수 영역 표현과 변환 개요

주기 신호의 특징

- 같은 주기의 기본파와 그 배가 되는 주파수를 갖는 고조파로 이루어짐

 -> 푸리에 급수 : 무한 급수의 형태를 띈 주기 함수들의 합

푸리에 급수

주파수 분석과 합성

- 주파수 분석 : 푸리에 급수에서 주파수 스펙트럼을 구함

- 주파수 합성 : 스펙트럼에 따라 정현파들을 만들고 이를 합한 결과 신호를 만듬

시스템 해석

- 시스템에 입력을 넣을때의 출력과 시스템의 특성을 파악하는 일

- 현실의 많은 현상들이 선형 시불변 시스템 LTI로 모형화 할 수 있어 LTI 시스템으로 해석해보자

시간 영역 해석

- 시간 영역 해석 : 시간 변화에 따른 출력과 특성 분석

- 연속 시스템 : 미분방정식으로 표현하여, 입력에 따른 변화뿐만아닌 초기 조건도 반영함

- 연속 시스템 적분(컨벌루션) : 외부 입력에 대해서만 반응표현하는 모델. 

 * 시스템 출력은 입력이 없어도 나올 수 있음.

임펄스 응답

- 응답 : 시스템에 입력을 줬을때 출력

- 임펄스 응답 : 임펄스 신호를 입력으로 넣었을때 출력

   * 임펄스 응답은 실제로 만들수는 없지만 수학적으로는 계산가능

 => 임펄스 신호는 t=0일때만 정의되어 시스템의 반응을 관찰할 수 있음.

LTI 시스템 콘볼루션 연산

- 매 시간마다 임펄스 응답이 있으면, 선형성과 시불변성에 의해 입력에 대한 출력을 얻을 수 있음.

- R 저항 회로의 임펄스 응답 h(t)를 가지고 계단 입력 u(t)를 넣었을때 출력을 구함.

콘볼루션 연산

- 임펄스 응답의 시간 t 변수를 임의의 시간 변수로 바꾸고, 시간 반전

- t를 이동시키면서 적분

컨볼루션 연산 주요 성질

- 교환 법칙, 결합법칙, 분배법칙

임펄스 응답의 의미

- 시스템 고유의 특성을 보여주며, 현재 출력에 대해 과거의 입력이 어느정도 반영되었는지 정도를 보여줌.

임펄스 응답의 한계와 미분방정식

- 한계 : 임펄스 응답과 입력의 콘볼루션으로는 입력이 주어질때의 시스템 결과만 구하므로 완전히 이해하기엔 부족

 + 외부 입력 없이 내부 상태에 의한 출력이 나올 수 있음.

 => 미분방정식을 통한 해석이 필요

LTI 시스템 미분방정식

- 선형 상미분방정식의 형태를 가지며, 미방의 해 = 시스템 출력

개요

- 맣은 기계들은 교류로 동작하며 정현파의 형태를 가짐.

- 발전기는 자계에서 세 쌍의 코일로 이루어진 회전자가 회전하여 크기가 같고, 위상이 120도씩 다른 세가지 전압 3상 전압이 발생

- 가정에서는 이 3상 전압을 변압 후 한개의 상, 단상 전압을 이용

교류 기전력

- 자속 내에서 회전자 하나가 회전하면서 얻는 기전력과 전압 최대치/순시치는 아래와 같다,

실효치, 평균치

- 실효치 : 제곱근(주기 제곱 합/주기), 교류 i와 동일한 전력을 사용하는 직류 I의 크기

- 평균치 : 한 주기 크기 합/주기

파고율, 파형률

- 파고율 = 최대값/실효값

- 파형률 = 실효값/ 평균값

벡터의 복소수 표시

- 복소평면에서 벡터 표현

기본 신호의 종류

1. (단위) 계단 함수 (unit) step function

- 단위 계단 함수는 t < 0에서는 0, t > 0에서는 1인 신호

- t > 0부터는 1인 특성을 이용하여, u(t)를 t_0만큼 이동 시킨 후 타 신호와 곱하여 잘라내 신호의 특정 구간 파악 가능

 (스위치 역활)

2. 사각 펄스 함수 retangular pulse function

- 사각 형태의 함수로, -a < t < a 구간에 대해 1 그 외에는 0이 된다.

- 타 함수와 곱하면 해당 사각 함수의 구간 만큼 on-off 스위치 역활을 한다.

3. 부호 함수 

- 양의 시간에선 1, 음의 시간에선 -1인 함수로 통신/제어에서 주로 활용

4. 단위 램프 함수 ramp function

- t = 0에서 시작하여 기울기가 1인 직선 함수

5. (연속, 단위) 임펄스 함수

- 임펄스 함수 impulse function은 디렉 델타 함수라고도 불리며 수학적으로만 정의된 함수

- 이 임펄스 함수를 특정 시간만큼 시킨 후 시스템에 입력으로 넣음으로서 해당 시간의 순간 결과를 추출할 수 있다.

6. 샘플링/싱크 함수

- 샘플링 싱크 함수는 사인파를 시간/ pi*시간 만큼 나눈 신호

- 주파수 영역에서의 해석에 사각 파와 함께 자주 사용

7. 지수 함수

- 지수 함수는 미분해도 형태가 바끠지 않으므로 해석에서 자주 사용됨.

- 람다가 실수, 순허수, 복소수에 따라 세가지로 구분할 수 있음.

- 실수인 경우 람다는 감쇠함수의 역활을 함.

 * 허수부분에서 계수 A를 극좌표 형태 |A| e^{j pi} 형태로 나타냄.

8.오일러 공식와 삼각함수

- 오일러 공식에서 지수가 순 허수인 경우의 복소 지수 함수는 실수 부분이 코사인 함수, 허수 부분이 사인 함수와 같은 관계를 나타냄

- 이 공식으로 삼각함수를 다음과 같이 정리 가능

신호에 대한 기본 연산

합, 곱, 값에 대한 반전, 이동, 척도조절

시간에 대한 반전, 이동, 척도 조절

신호 미/적분