집밖은 위험해

열전 효과

- 제백효과 : 두 금속 온도차 -> 전류

- 펠티에효과 : 두 금속에 전류 -> 온도 변화

- 둘다 아니면 홀효과

전계 세기

- 직선 원통 도체

평행판 콘덴서에 정현파 인가시 변위 전류

- 변위 전류 : 평행판 사이에 흐르는 가상의 전류

멕스웰 방정식

미분 회로

회로 문제 - 정현파 전압 가할시

1. R 회로 : 극좌표, 삼각함수좌표, 지수함수 좌표

저항 구하기

1. 자속과 t 초동안 쇄교시 전하량이 주어질 떄의 저항

상호 인덕턴스 M

역률 구하기

1. R L 직렬회로

2. R L 병렬회로

4단자 정수

- 임피던스 파라미터

- h 파라미터

- 영상 파라미터

라플라스 & Z 변환

다이오드 정리

- 서미스터 : 온도 변화에 따라 저항이 바뀜

반전 증폭기 입력 임피던스 : 1M ohm

- 왜율 = 전고조파 rms/기본파

BJT와 FET 비교

- BJT : I_b -> I_e 전류 증폭. 스위치, 잡음/대역폭/속도 크다,   집적도 작다.

- FET : I_g -> I_d 증폭, 전압 증폭,   <->,            집적도/열 안정성/입력임피던스 크다.

디지털 변조 : QAM, PSK, ASK, FSK

펄스 변조 : PCM, PPM, PAM, PWM

부궤환 회로 특징 : 이득/일그러짐율/잡음 감소,   안정도/대역폭 증가

반전/비반전 증폭기

연산증폭기- 산술연산

미분기와 적분기

연산 증폭기 응용분야

- 선형 증폭기 : 반전/비반전 증폭기

- 연산 증폭기(연산기) : 미분, 적분, 더하기, 빼기

- 비교기, 파형 발생기

연산기

1. 미분기

- 반전 연산 증폭기에 저항 R1 대신 캐패시터 C를 사용하여 미분 연산을 하는 회로

2. 적분기

- 반전 연산 증폭기에 저항 R2 대신 캐패시터를 사용하여 적분 연산을 구현한 회로

3. 가산기(가산 증폭기)

- 여러 입력 신호를 선형 합하여 증폭하는 회로

- 모든 저항이 같은 경우에 출력 전압은 입력 전압의 합의 반전이 된다.

4. 감산기

- 반전 연산 증폭기의 결과와 비반전 연산 증폭의 결과를 합

- 저항이 모두 같다고 가정하면 두 입력 v2, v1간의 차이가 결과 전압으로 나온다.

회로와 집적회로

- 개별 소자 회로 : 소자들을 모아 구성한 회로

- 집적 회로 : 많은 소자들을 집적하여 만든 회로

집적회로에서의 연산증폭기

- 여러 소자들을 모아 이상적인 증폭기에 만든 것

- 편리, 소형, 신뢰, 저가로 아날로그 시스템에서 널리 사용

- 기본적으로 차동 증폭기를 사용.

증폭기의 종류

- 전류 증폭기 : 입력 전류 i_I에 의해 출력단 종속 전류 A_i * i_i이 조절되는 증폭기

  + 이상적인 전류 증폭기 : 전류 이득 A_i = inf, 입력 저항 R_i = 0, 출력 저항 R_o = inf(부하로 많이간다)

- 전압 증폭기 : 입력 전압 v_i에 의해 출력단 종속 전압 A_v * v_i가 조절되는 증폭기

  + 이상적인 전압 증폭기 : 전압 이득 A_v = inf, 입력 저항 R_i = inf, 출력 저항 R_o=0(부하에 많이 걸린다)

- 전달 컨덕턴스 증폭기

- 전달 저항 증폭기

연산 증폭기

- 두 입력과 하나의 출력으로 구성 + +V_CC(Source), -V_EE(sink)의 이중전원사용

- 비례 상수 A_o는 개루프(open loop) 이득을 의미

   =>v+는 위상반전없이 증폭, v-는 위상반전되어 증폭

- 출력은 공급 전원인 -V_EE <= v_o <= +V_CC 범위로 제한되며, 초과시 해당 범위로 포화)

- 이상적인 연산증폭기에 가깝게 만들기 위해 수십개의 트랜지스터 사용 + 개루프 이득이 아주 큼

연산증폭기와 등가회로

- 이상적인 연산 증폭기에 가깝게 입력 저항은 무한대, 출력 저항은 0, 이득은 아주 크게 만들어 진다.

- A_o가 100k라 할때, 1V 출력을 얻으려면 v_i는 10uV면 된다

- 포화 전압이 +-5V인 경우, v_가 +-50uV를 넘어가면 포화된다.

 => 비교기로 사용하려면 포화시키면 된다.

 + uV 단위는 매우 작으므로 0으로 보자.

- 증폭기로 사용하기 위해서는 선형영역이 넓어지는것이 좋다.

연산증폭기의 동작

- 비교기 : V_in이 +V_cc, -V_EE로 포화시 비교기로서 비선형적인 동작

- 증폭기 : V_o의 일부가 반전 입력으로 궤환. 궤환 비율은 분배 저항 R1, R2로 결정

      -> 출력이 반전 입력단으로 들어가므로 기존의 출력 v_o와 위상이 반대로

      -> -가 되어 출력에 반영되어 개루프때보다 이득이 줄어든다.

      => 부궤환을 통해 선형영역을 늘린다 => 증폭을 조절하기 좋아진다 => 증폭기로 사용한다.

가상 단락

1. 연산증폭기의 입력 저항 R_i는 무한대이므로 두 입력 사이에는 (i+) + (i-) = 0전류가 흐르지 않아 개방 회로가 된다.

2. 연산 증폭기의 전압 증폭률 A_v = 무한대에 가까워야하나 v_o가 포화되지 않으려면 v_i는 0에 가까워야한다.

 => v_i = 0이 된다는것은 단락 상태를 의미한다

    *개방시는 V가 무한대가 됬었고, 단락시에는 0이므로

- 가상 단락 : 개방과 단락의 성질을 동시에 가지는 것 => 연산 증폭기 해석에 유용

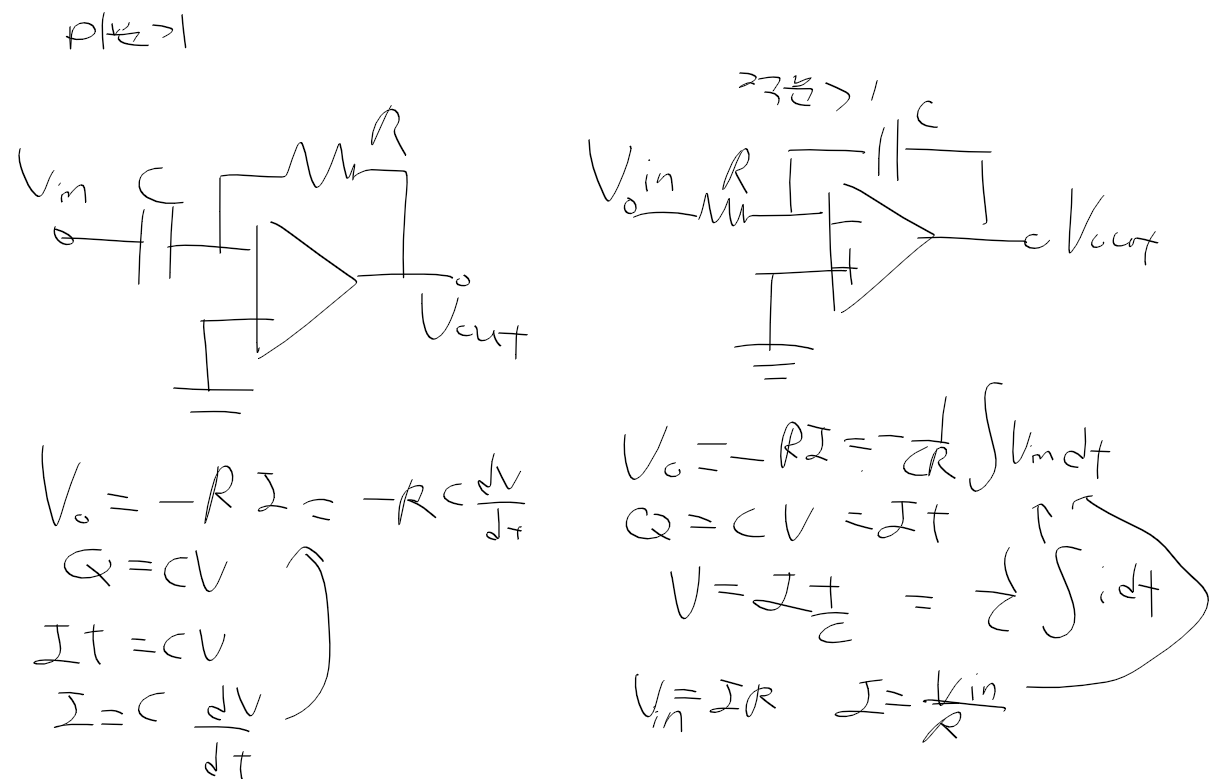
반전 증폭기

- 비반전 입력은 접지, 반전 입력에만 입력을 주는 증폭기

1. 비반전 입력 : 접지처리되어 입력단 전압 v_+ = 0 

2. 단락 성질 : 반전 입력단의 전압 v_-는 비반전 입력단의 전압 v_+과 같으나 비반전 입력 전압이 0이다.

               => Vs와 v_- 사이 전위차가 존재하므로 저항 R1에 전류가 흐른다.  => i = Vs/R1

3. 개방 성질 : 입력 저항이 무한대 = > 개방 상태 => 반전 입력단자에 가지 않고, R2로 간다.

              => 출력단 전압 v_o는 저항 R2에서 전압 강하된 전압을 뺀 정도가 된다.

              => v_o = (v_-) - (R2 * i) = -R2 * i

- 정리하면 폐루프 이득 A_v를 구할 수 있으며, 이득 A_v는 R1과 R2를 조절하여 바꾼다. 

 * 입출력 전압의 위상은 폐루프 이득이 음수이므로 반대가 된다.

비반전 증폭기

- 비반전 증폭기는 +에 입력을 - 단자에 접지를 하는 증폭기로 앞서 본 가상 단락의 개념으로 증폭도, 출력을계산하자

비반전 증폭기의 궤환 전압과 궤환 전압 이득, 전체 저항

- 두 저항을 이용한 전압 분배를 떠올리자. 궤환 전압 v_f와 전압 궤환 이득 beta를 구할 수 있다.

- 전체 입력 저항 R_if는  V_in = (V_+) - (V_-)로 부터 구할 수 있다.

N형 BJT 구조

- C-B 다이오드는 종속 전류원으로 동작

BJT 동작

- B-E에 순방향 바이어스, C-B에 역방향 바이어스를 인가 시 BJT는 활성 상태가 된다.

1. 바이어스 인가 전

- 바이어스 인가 전에는 B-E 사이 공핍층에 의해 전장 E_BE, C-B 사이에는 전장 E_CB가 존재한다.

- E_BE는 전자가 E에서 C로 이동하는 것을 막고 있다.

- E_CB는 정공과 전자를 분리하여 결합을 막아 이동하는 것을 돕고 있다.

=>B-E에 순방향 바이어스를 인가하면 전자 이동을 막고 있는 전장 E_BE를 줄일 수 있다.

=>B-C에 역방향 바이어스를 인가하면 전장 E_BC가 더 두터워져 정공과의 결합을 줄여 더 쉽게 이동할 수 있게 된다.

2. 바이어스 인가

- 이미터로 전자가 주입되고, 이미터의 전자가 컬렉터로 이동하는 중 일부는 베이스의 홀과 재결합하여 사라짐.

  => 사라진 홀은 V_BE 단자로 보충

- 나머지 이미터 전자들은 확산하면서 베이스를 넘어가 컬렉터에 모이게되고(수집) 전류가 흐르게 된다.

 => 바이어스 인가전에는 전위장벽 E에 의해 넘어가지 못하던 전자들이 E로 주입되어 넘어가면서 B에서 일부는 재결합하고 나머진 넘어가면서 흐른다.

BJT 바이어스

- BJT를 활성 시키기 위한 방법

- B-E 사이에 있는 다이오드는 온도 영향을 크게 받음 -> 저항 R_B를 직렬연결하여 I_B 제어

BJT 증폭기와 구성

- CB : E 입력, C 출력, B 공통단자

- CE : B 입력, C 출력, E 공통단자

- CC : B 입력, E 출력, C 공통단자

- CB 증폭기 : A_v, A_i가 증폭, 종속 접속을 통해 이득을 키운다. (beta = 50)

- CE 증폭기 : A_i가 1보다 약간 작다. 입/출/전압/전류 위상이 동위상 (alpha=1)

- CC 증폭기 : A_v가 1보다 약간 작으며, 고입력 저항 회로(임피던스 정합회로) 

소신호 등가회로(=교류 등가회로)

- 아래 그림은 CE 소신호 등가회로의 4단자 회로망 형태

제너 다이오드

- 제너 항복 : 역방향 바이어스 인가시 전류가 급격히 감소하기 시작하는 전압 지점

 => 제너 다이오드에 역방향으로 인가 전압을 높여도 제너 다이오드에 걸리는 전압은 일정하나

      역방향으로 흐르는 전류가 급격히 커짐

정류 회로

- 대부분의 전자 장비는 직류 전원을 이용

- 송전 선로에서 경제성(변압, 변환 등)을 이유로 교류로 송전하고, 가정에서는 교류를 직류로 정류해 사용.

반파 정류기

- 교류 전원을 받아 변압 후, 다이오드를 통해 반파 정류하는 회로

- 가장 낮은 효율 간단

전파 정류

- 중간 텝(접지역활)을 이용해 교류 전체 파형을 정류함.

- 권선 길이가 반파 정류회로의 2배, 세게 작용하는 교류 역전압, 전압이 반토막 난다.

브리지 정류 회로

- 4개의 다이오드를 이용한 전파 정류 회로

- 효율이 좋으나 많은 다이오드 필요, 순방향 전압강하가 크다.

평활회로

- 정류 후 맥류에는 고조파 교류 성분을 포함해서 완전한 직류는 아님.

 => 캐패시터 C를 정류회로에 병렬로 연결

 => 공급 전류가 떨어지면 저장된 에너지 방출하여 평활화

- RC 회로 시정수 : 충전시 63.2%까지 도달하는 시간, 방전시 36.8%까지 도달하는 시간

 => 시정수가 크면 방전이 오래 걸리므로 직류 모양에 가까워 진다.

- 리플 : 직류 중 남아있는 교류 성분

클리퍼

- 일정 파형만 잘라서 나머지 부분만 통과하는 회로

클램퍼

- 파형은 유지하되 0V가 아닌 일정 기준 전압으로 올리거나 낮추는 회로

비정현파 발생

- 교류 회로는 가능한 전압/전류가 교류가 되도록 설계하지만 발전기에선 전기자 반작용, 변압기에선 자기포화, 히스테리시스 현상 등으로 정현파가 일그러짐. => 왜형파/비정현파

- 비정현파 = 연속파(대칭파 + 비대칭파) + 불연속파

비정현파 실효값과 왜형률

- 비정현파 실효값 = 기본파 + 전고조파의 rms

- 왜형률 = 전고조파 rms/기본파 rms

* 맥동률 = 교류분/직류분, 불평형률 = 역상분/정상분

비정현파 실효값 왜형률 문제

비정현파 회로 계산

1. R 회로 :  v와 i는 동상이므로

2. L 회로 : i는 v보다 90도 늦으므로

3. C 회로 :  i는 v보다 90도 앞서므로

RLC 직렬 회로와 공진

- 다음의 RLC 직렬회로에 비정현파 인가시 n고조파 임피던스, 공진 주파수 등은 다음과 같다.

- 비정현파 전압 v와 임피던스로 전류 i를 구할 수 있으며

- n 고조파 공진시 해당 고조파 성분은 부하에 가지 않고 LC회로로 바이패스된다.

비정현파 전력

- 비정현파 v와 i가 주어질 때, 순시전력 p = vi를 이용하면 된다,

* 주파수가 다른 전압과 전류의 전력은 0이 되므로 같은 주파수간의 전력만 구하면 된다.

* 피상 전력 S는 인가 전압 v의 순시치 x 인가 전류 i의 순시치로 구한다.

* 유효 전력 P는 각 고조파의 (V 순시치 x I 순시치)들의 합으로 구한다. 

   + (위상차가 없는)같은 고조파의 경우 P = V I cos theta에서 theta는 0이 되므로 cos theta는 1로 놓고 본다!

예제

2전력 계법

- 불평형 3상 3선 회로를 2개의 전력계로 구한 전력의 합/차로 3상 전력을 측정하는 방법

- 3상 유효 전력 P = P1+P2

- 3상 무효 전력 Q = root(3)(P1 - P2)

- tan theta는 Q/P로 구할 수 있다.

재정리

- 대칭 3상회로 : 기전력=, 위상각 2pi/3

- 대칭 3상 전원 회로 : 대칭 3상 회로 + 내부임피던스=

- 평형 3상 부하 회로 : 3상 부하 임피던스 =

- 평형 3상 회로 : 대칭 3상 전원 회로 + 평형 3상 부하 회로

=> 불평형 회로 = 3상 부하 임피던스가 같지 않은경우?

대칭 좌표법

- 평형 회로 문제를 쉽게 계산하기 위한 방법

- 상순이 a,b,c인 평형 3상전압 V_a1, V_b1, V_c1 

    + 상 순이 반대인 평형 3상전입 V_a2, V_b2, V_c2

    + 방향과 크기가 같은 3상 전압 V_a0, V_b0, V_c0

   = 불평형 전압 V_a, V_b, V_c를 얻는다.

=> 반대로 불평형 전압을 영상분/ 정상분/역상분으로 분해 가능하다.

    - 영상분 : 방향과 크기가 같은 전압성분

    - 정상분 : 상순이 a, b, c인 전압성분

    - 역상분 : 상순이 반대인 전압성분

- 벡터 연산자를 이용하여 불평형 3상 전압 벡터를 정리하면..

- 전류도 동일한 관계를 가진다.

- 대칭분 = 영상분 + 정상분 + 역상분

- 정상분만 존재하는 경우를 평형 3상 전압

- 역상분이 존재하지 않은경우 => 불평형률 = 0 => 평형 3상 전압

예제

대칭 3상 교류 발전기

- 대칭분 행렬을 통해 기전력, 단자전압, 전류를 다음과 같이 정리 할 수 있다.

- 영상분, 정상분, 역상분에 대한 임피던스가 주어지면 각각의 단자 전압은 다음과 같다.

- 위 3상 교류발전기가 대칭 3상 발전기이므로 a상으로 각상 기전력을 바꾼 후 단자전압을 다음과 같이 정리할 수 있다.

3. 3상 회로 고장 계산

1) 1상 지락

- a상 지락 시, b와 c상에 흐르던 전류들이 사라지고 i_b = i_c = 0, 접지된 a쪽으로 흐르므로 접지전류 i_a를 구해야한다.

 * a로 전류가 흐르나, 부하가 존재하지 않으므로 V_a =0이 된다.

2) 2상 지락

- b, c상 지락

   => a상으로 흐르는 전류가 없어진다 i_a = 0.

   => 부하가 없으므로 단자전압 v_b = v_c =0이 된다.

불평형 3상 회로

- 3상 교류는 평형 회로로 설계 유지되지만..

 1. 전원이 대칭이나 부하가 불평형

 2. 사고로 인해 전원/부하 모두 불평형인 경우

=> 키르히호프 법칙 이용하자

* 평형 3상 회로 : 기전력=, 내부임피던스=, 위상차 2pi/3, 부하 임피던스=

1) 중성점 접지식 Y-Y 회로

- 비대칭 3상 기전력, 불평형 부하가 주어지고, 중성점 O와 O'사이 임피던스 Zn이 존재

 + 전원 중성점 O를 영전위라 가정하면 => 3상 부하 중성점 O'는 전위 Vn 가짐

- 밀만의 법칙으로 중성점 전위 Vn을 구할 수 있으며 이 Vn으로 각 상의 전류를 구할 수 있다.

2) 중성점 비접지식 Y-Y 회로

- 위 중성점 접지식 Y-Y회로에서 Y_n = 0, I_n=0으로 놓고 계산하면 된다.

+ 전원이 대칭인 경우 : 상이 2pi/3씩 차이나고, 기전력=, 내부임피던스=

   => E_a = E, E_b = a^2 E, E_c = a E로 계산 가능!

3) 불평형 델타 부하

- 다음의 델타결선 불평형 부하에 3상 전압 인가시 I_a, I_b, I_c는 아래와 같이 구할 수 있다.

예제

3상 회로 전력

- 3상 회로 전력 P는 델타나 와이결선이나 상전압 V과 상전류 I, 위상차 theta가 주어질때 다음과 같이 구하면 된다.

- 실제로 전압/전류계로는 선전류의 실효값, 선간 전류의 실효값을 측정하기 쉬우므로 다음과 같이 전력을 계산한다.

- n 상의 경우 선전압, 선전류, 전력은 다음과 같이 계산한다.

예제

3상 시스템

- 주파수는 같고, 위상이 다른 세 교류 기전력을 사용하는 방식-

- 3상 기전력을 3pi emf라 부름.

3상 방식의 분류

1) 대칭 여부

  - 대칭 3상 방식 : 3개의 기전력이 같고, 위상차가 2pi/3씩 다른 경우

  - 비대칭 3상 방식 : 그렇지 않은 경우

2) 대칭 전원 여부 

   - 대칭 3상 전원 : 대칭 3상 방식 + 각 상의 내부 임피던스가 모두 같다.

   - 비대칭 3상 전원 : 그렇지 않은 경우

3) 부하의 같은 지여부

  - 평형 부하 balanced load : 각 상의 임피던스가 같은 부하

  - 불평형 부하 : 각 상의 임피던스가 다른 부하

4) 평형 여부

  - 평형 3상 회로 : 대칭 3상 전원 + 평형 3상 부하

           => 각 상의 기전력(대칭) 임피던스(대칭 전원)나 부하(평형)가 모두 같고, 위상차도 2pi/3씩 차이나는 회로

  - 불평형 3상 회로 : 그렇지 않은 회로

=> 대칭(기전력 =, 위상), 대칭 전원(내부 임피던스 =), 평형 부하(부하 Z = ), 평형 회로(대칭 전원 + 평형 부하)

교류 회로 결선 방식

1) 성형 결선 star connection

- 동일 극성인 단자를 0점(중성점)에 묶어 결선

- 각 상의 외부 단자는 전원 단자로 이용

2) 환상 결선 ring connection

- 각 상의 극이 다른 단자 끼리 직렬 접속해 환상(원) 모양으로 접속

- 각 상의 단자를 전원 단자로 사용

3) Y 결선 : 3상으로 만든 성형 결선

4) 델타 결선 : 3상으로 만든 환상결선

대칭 3상 교류 기전력

- 순시치 v_a, v_b, v_c는 모두 크기와 주파수가 같은 정현파, 위상만 2pi/3 씩다름

- 벡터연산자 a를 이용한 a, b, c 상전압 표시

- Y-Y 결선

예제

- 델타 결선

재정리

- 대칭 3상 회로 : 기전력=, 2pi/3씩 위상차

- 대칭 3상 전원 회로 : 대칭 3상 회로 + 내부 임피던스 =

- 평형 부하 3상 회로 : 3상 부하 임피던스 =

- 평항 3상 회로 : 대칭 3상 전원회로 + 평형 부하 3상 회로

     => 기전력/내부 임피던스/부하 임피던스= + 위상차 2pi/3

평형 3상 회로

1) Y-Y 회로 (전원, 부하 모두 Y결선)

2) Y-델타 회로

* 델타-Y, 델타-델타는 생략

예제 1

예제 2

예제 3,4

V결선

- 델타 결선에서 한 상의 전압/임피던스가 없는 경우

- 이용률 = 0.866(V결선 두대 출력/2대 출력 합)

- 출력비 = 0.577(V 결선 두대 출력/델타 결선 출력)