대략 정리
- 지금까지 다양한 기본 신호와 시스템, 컨볼루션 연산 등을 살펴봄
- 신호는 연속 신호와 이산 신호로 구분 할 수 있으며, 주기 신호 여부에 따라 푸리에 급수, 푸리에 변환을 통해 해석.
- 이후 연속 신호는 라플라스 변환, 이산신호는 z 변환으로 해석하며, 신호는 주파수 스펙트럼, 시스템은 전달함수로 알아볼 예정
푸리에 변환
- 비주기 신호도 해석 하기 위해서 기존의 푸리에 급수에서 주기를 무한대로 늘려 해석
- 푸리에 급수의 경우 주기 신호인 만큼 주기가 셀수 있는 만큼 존재하였으나, 비주기 신호의 경우 다양한 주기의 신호들이 존재한다고 봄 => 연속적인 주파수 스펙트럼을 얻음으로서 적분으로 표현

푸리에 급수와 변환 의 관계와 조건
- 푸리에 변환은 모든 구간에서 디리클레 조건(적분 시 수렴 가능여부)을 만족해야함
+ 주기 신호를 푸리에 변환하는 경우? 주파수가 이산적이므로 이산함수가 된다.


주파수 응답
- 시간영역에서의 시스템 응답 : 콘볼루션 연산 혹은 미분 방정식 이용 -> 어려우며, 주파수 정보 부재
- 시스템을 주파수 변환하여 해석하는것이 좋음
-> 주파수 특성 파악 용이, 시간 영역에서 콘볼루션은 주파수 영역에서는 곱 연산임. 미방의 경우 쉽게 결과 취득
- 주파수 응답 H = 주파수 영역에서의 Y/X

복소 정현파 입력에 대한 주파수 응답(콘볼루션 연산)

주파수 응답을 이용한 시간영역에서의 시스템 출력 구하기
1. 입력, 임펼스 응답 -> 푸리에 변환
2. 입력 스펙트럼과 시스템 주파수 응답 곱 연산 -> 출력 스펙트럼
3. 푸리에 역변환으로 시간 영역에 대한 출력 신호 구하기

주파수 응답 및 필터
- 주파수를 활용하기 좋은 분야로 필터가 있음.
- 주파수 선택 필터 : 필요한 성분만을 걸러내는 필터
종류 : 저역 통과/고역 통과/대역 통과/대역 저지 필터
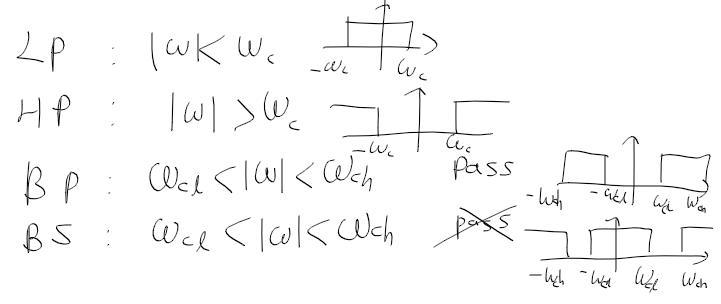
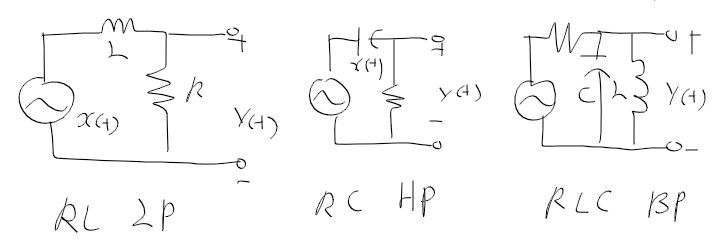
전기 회로를 이용한 필터
- RL 저역통과, RC 고역통과, RLC 대역 통과 필터
'기타 > 신호, 회로, 제어' 카테고리의 다른 글
| 신호와 시스템 - 8. 이산 신호 처리 (0) | 2022.03.11 |
|---|---|
| 신호와 시스템 - 7. 라플라스 변환 (0) | 2022.03.10 |
| 신호와 시스템 - 5. 연속시간 푸리에급수 (0) | 2022.03.09 |
| 신호와 시스템 - 4. 시간 영역 해석 및 응답 (0) | 2022.03.09 |
| 회로이론 - 2. 정현파 교류 (0) | 2022.03.08 |