컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법

기하 정렬/기하 관계의 필요성

 

앞서 살펴본 매칭 과정은

 

지역 정보. 특징점의 기술자만을 사용하여 대응점들을 찾았다.

 

하지만 동일한 물체끼리는 기하 변환 관계를 가치는데, 이 기하 정렬 geometrical alignment조건 을 고려할 필요가 있음.

 

 

www.cc.gatech.edu/~hays/compvision/proj2/

 

 

 

 

기하 변환을 위한 최소 제곱 법

 

그동안 선형 모델을 구할때 최소 제곱법을 자주 사용했었는데,

 

컴퓨터 비전 문제에 최소 제곱법을 사용해보자.

 

위와 같은 두 영상에서 대응쌍 구했다고 하자

 

X = {(a1, b1), (a2, b2), . . ., (a_n, b_n)}

 

이 대응 쌍들은 기하 변환을 통해 얻었을탠대

 

회동, 이전, 크기 변환을 포함한 기하 변환 행렬 T로 나타내자

 

 

 

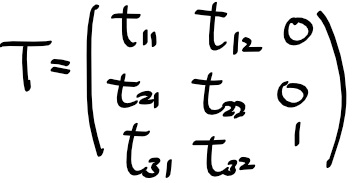
기하 변환 행렬 T로 a_i들 맵핑하여 b_i'를 얻을수 있게 된다.

 

 

 

 

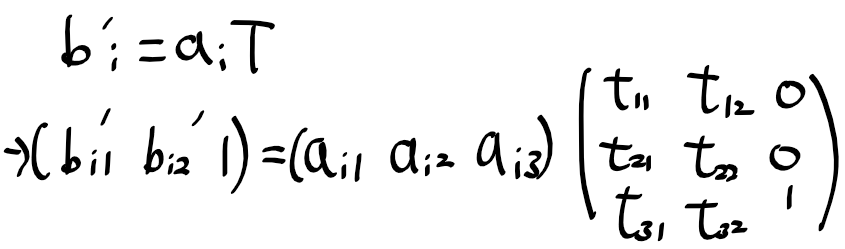
실제 b_i와 a_i를 변환하여 얻은 b_i'사이에는 오차가 존재할텐대

 

이 오차를 최소화 하는 변환 행렬 T를 구하는게 목표가 되겠다.

(변환 행렬의 파라미터 6개를 구한다)

 

 

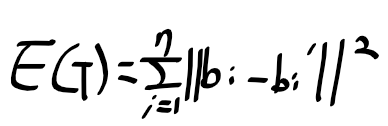
오차 E(T)를 기하 변환 행렬 T의 각 요소들로 편미분한 것을 0으로 하여 식을 얻고

 

행렬식을로 표현하면 아래와 같이 정리할 수 있다.

 

 

 

 

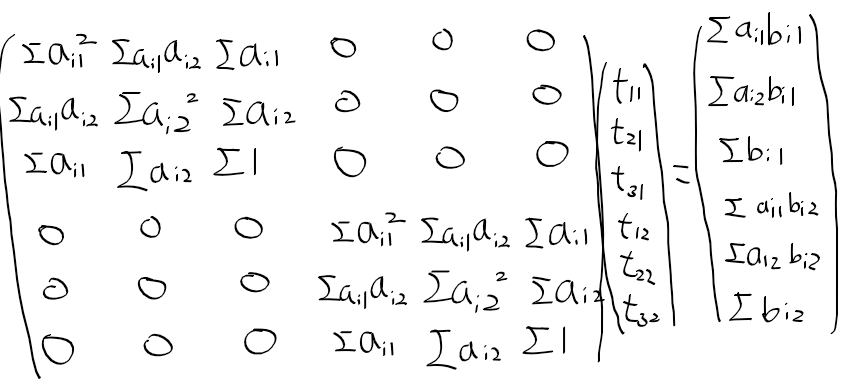
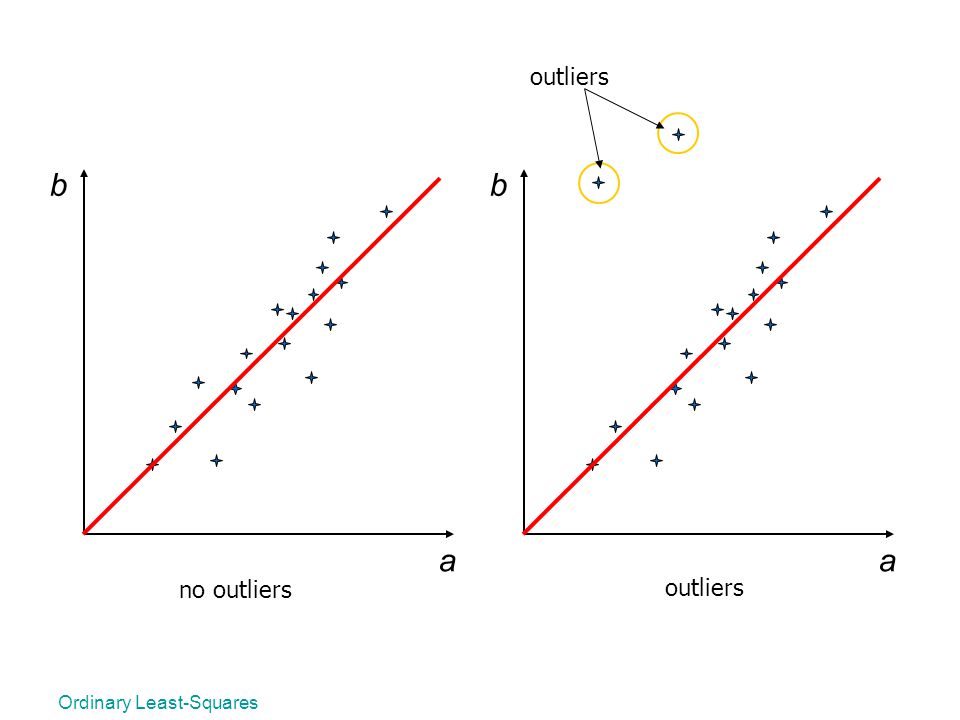
최소 제곱법의 한계

 

하지만 최소 제곱법은 오차가 정규 분포를 따르는 경우 정상적으로 동작한다.

 

그래서 아웃라이어의 영향을 크게 받는데,

 

아웃라이어를 제거하거나 이에 강인한 기하 변환 행렬을 구할 수 있는 방법이 필요하다.

 

https://slideplayer.com/slide/2342847/