집밖은 위험해

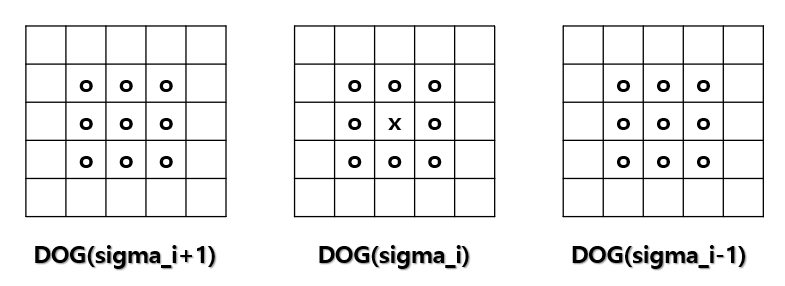
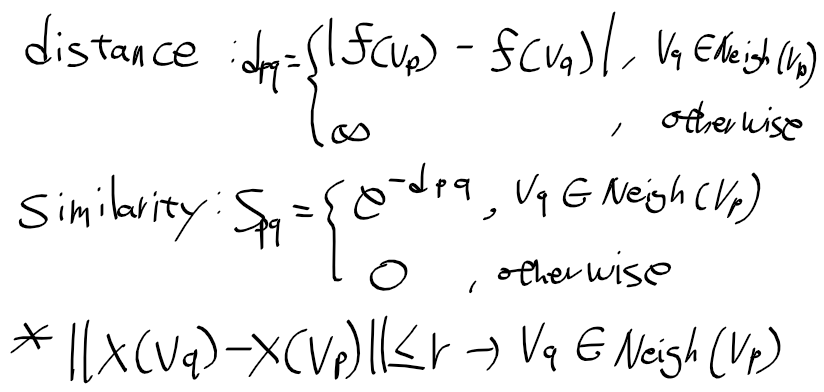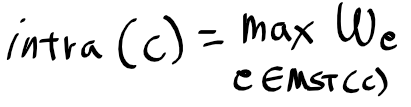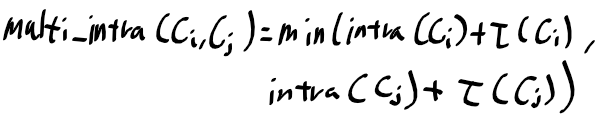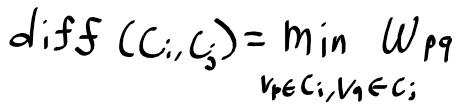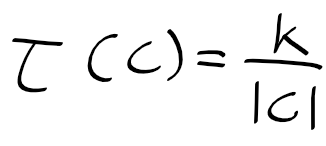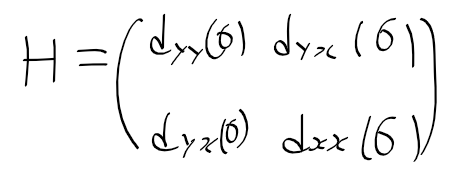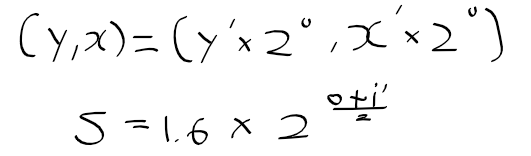컴퓨터 비전 정리를 중간?

공부할 내용들 중 실제로 1/3정도 쯤 온것 같기도 한데

집에서 혼자서 해서 그런가 참 하기가 싫다.

중간 중간에 쉬었다가 하다가 그렇게 나마 반복하고있는데

점점 하기싫어 지는 기분이 커지더라

분명 처음 이 내용을 공부할때보다는 이해되는 부분은 많았다.

오츠 알고리즘 때부터 최적화 기법으로 가장 좋은 이진화 임계치를 찾는다고 하였는데,

통계/대학 수학/공업 수학 공부를 하면서 클래스간 분산이 최대가 되도록 하는 임계치를 찾는 다는 말이 이해가 되더라

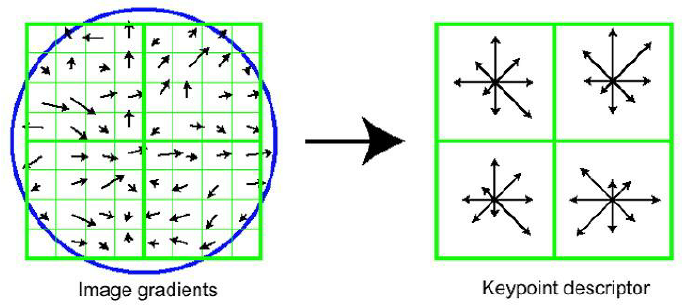
이후 내용도 특징 벡터, 기술자라는 용어들이 햇갈렷엇다

키포인트나 기술자나 같은게 아닌가. 싶엇는데

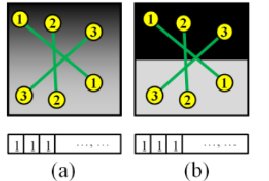
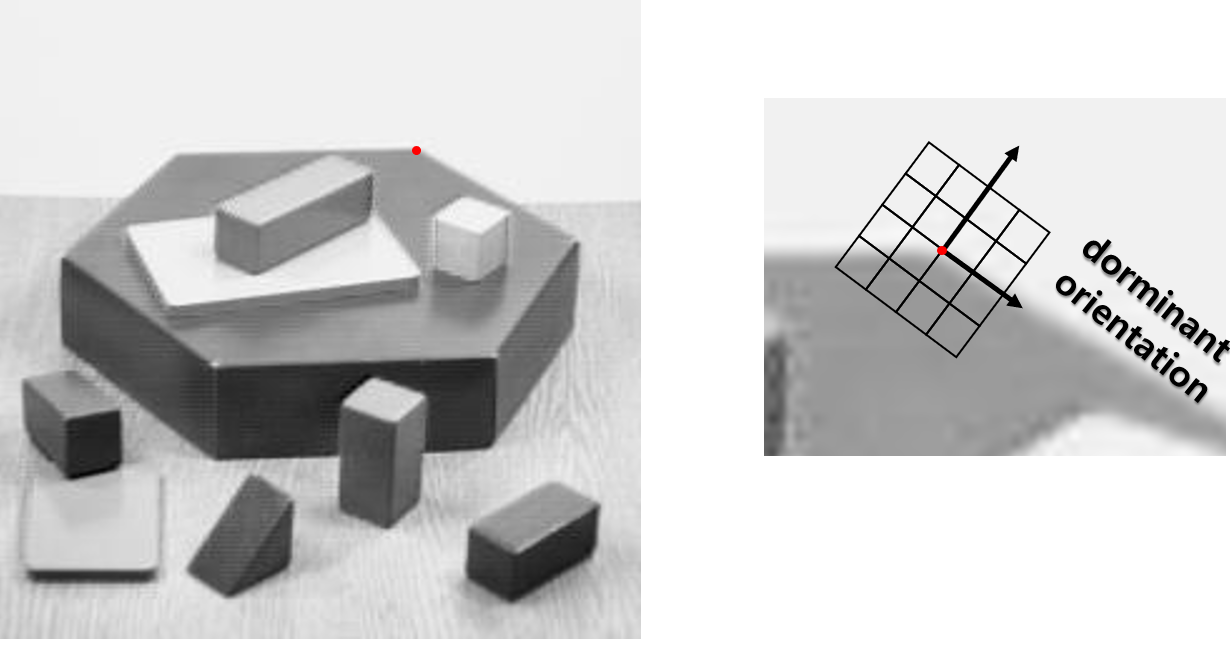
키포인트가 주어지면 이미지 패치로 구한 키포인트와 주변 픽셀에 의한 성질이 키포인트고

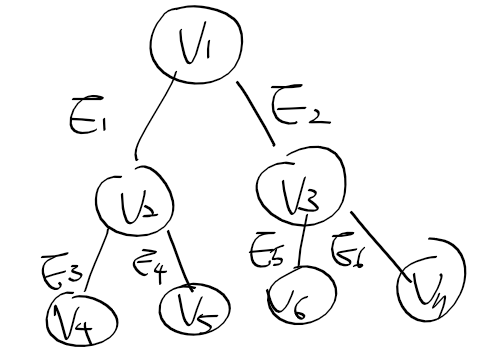
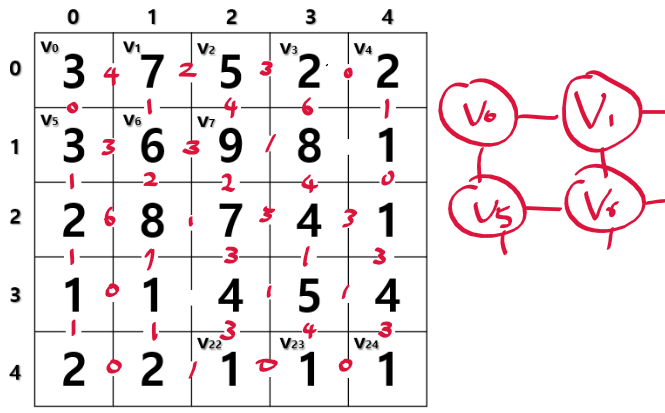
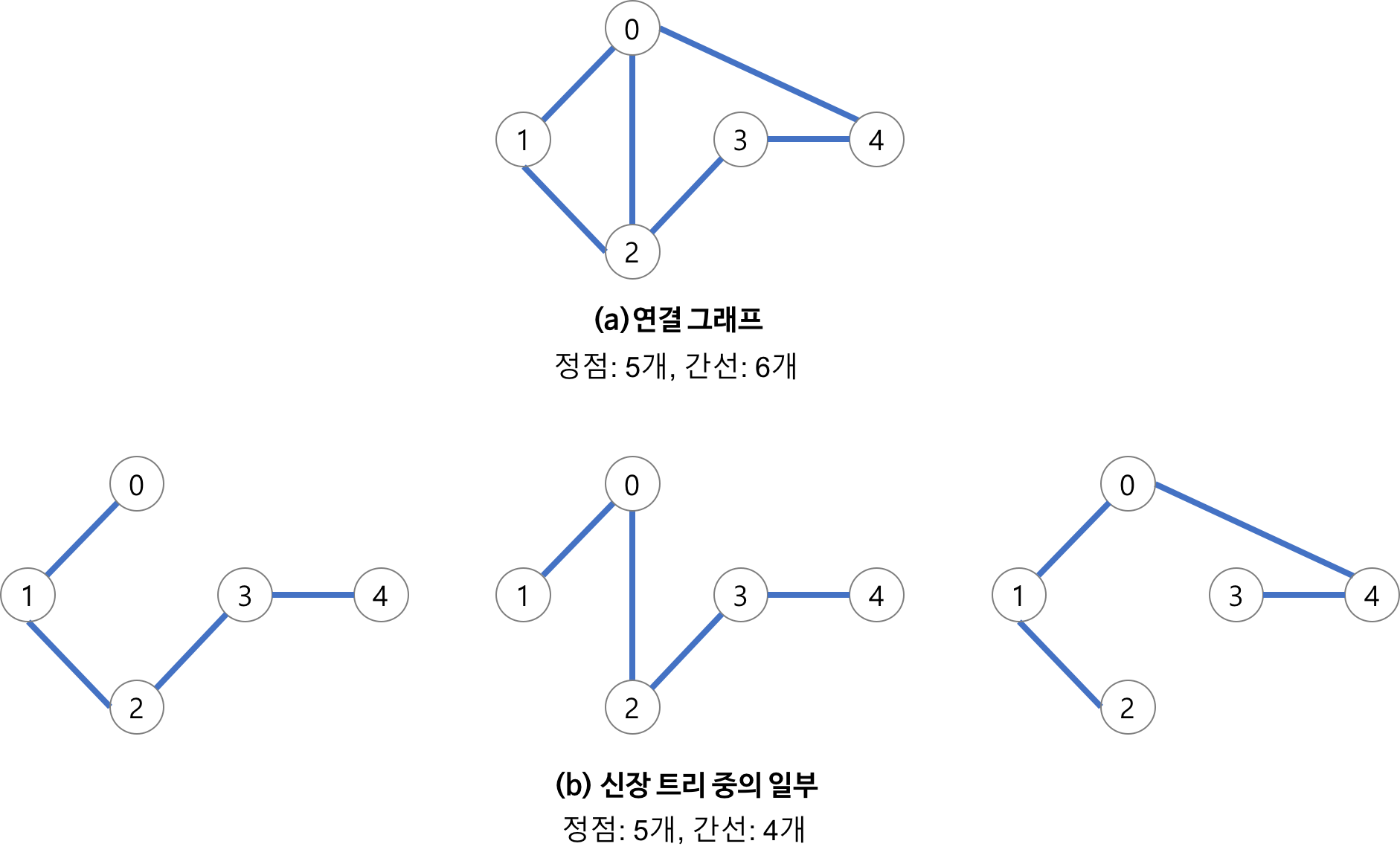
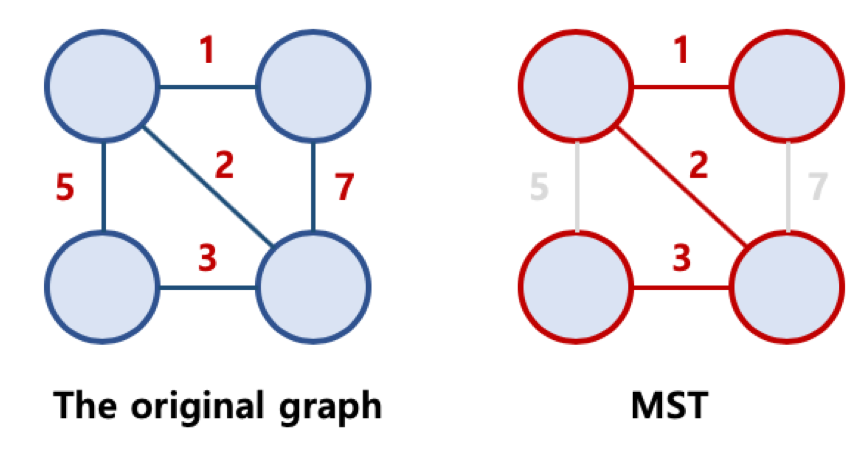
그래프에 대한 내용도 어느정도 이해되기 시작했다.

내가 이전에 이 공부를 여러번 할때마다 힘들었던건

자료구조, 알고리즘, 선형대수, 확률 통계론, 공업 수학 등에 대한

터미놀로지, 개념들에 대한 이해, 빈 틈이 너무 많았기 때문이었던것 같았다.

당장 당장 모르는 개념들 간단히 필요할때마다 보면 잠깐 찾아보면 되겠지 싶었으나

그 개념이 나오기 까지의 배경에 대한 일들이 전혀 모르니

개념에 대한 정의만 알아서는 뭘 할수가 없었다.

이걸 가장 크게 느낀 개념이 최대 우도법인데

이전에 본 서적에서는 최대 우도법이라는 표현을 쓰고있어서 

우도 함수를 최대화하는 모수를 찾는 방법 이라는 단순 설명 만으로는 이해하기 힘들었었다.

그런데 확률, 통계론을 공부하는 과정에서

우도를 가능도라는 이름으로 바꿔서 보고, 모수란 무엇인지

확률 분포와 모수의 관계, 빈도론자와 베이지안 관점, 함수의 다변수 미분 그라디언트 등에 대해서 이해하고 나서야

최대 가능도 방법에 대해 완전히 받아들일수 있게 되었다.

이게 컴퓨터 비전을 처음 공부하기 시작한지

2년이 지나서야 가능했다.

지금 이 내용들이 이해가 가면서 다른 문제가 생겼는데

그 동안 시행착오를 하면서 지친것인지,

급한 마음이 없어져선지

열심히 하고싶은 마음이 사라졌고

내가 왜 이걸 하는지 의문이 들더라

학교 다닐때는 어쩔수 없이 공부 해야만 했기 때문에 열심히라도 했었는데

지금은 이 비전 분야를 공부해 나가고싶어서 공부하지만 이전 처럼은 열심히가 되질 않는다.

컴퓨터 비전에서 하고싶은게 무엇인가

내가 우선 컴퓨터 비전 분야에서 하고싶은것들은 다음과 같은 것들이 있겠다.

이미지 매칭

영상 분할

물체 인식

이미지 매칭에 필요한 특징들과 기술자들을 살펴봤고,

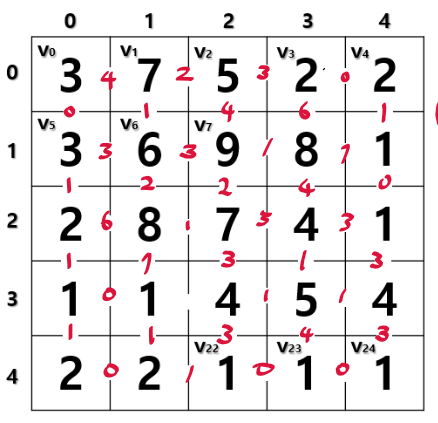
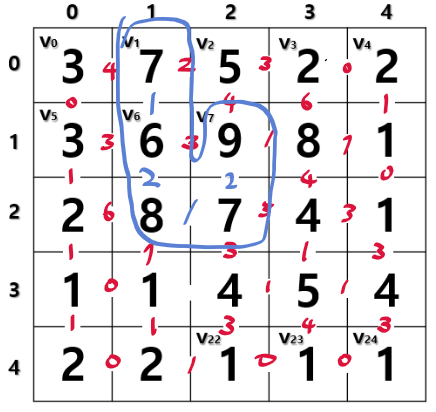
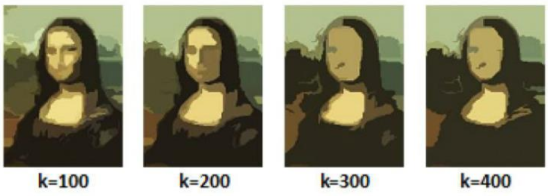
영상 분할의 경우 전통적인 방법과 기본적인 그래프를 이용한 방법을 살펴봤다.

물체 인식의 경우 이전에 단순 분류 cnn가지고 만들어보는 수준이었지 세부적인 분류나 다중 물체인식을 어떻게 하는지

논문 찾아가면서 삽질하다가  포기 했었다.

지금이라면 이해할수 있을것 같긴한데

너무 글만쓰는것 같기도 하고

이전 글에서는

이진 기술자들이 사용되는 이유와 특징 벡터를 추출하는 방법, 몇가지 경우의 조사 쌍들을 살펴봄

이번에는 대표적인 이진 기술자들인 BRIEF, ORB, BRISK를 살펴보자

BRIEF Binary Robust Indepent Elementary Features

ref : medium.com/data-breach/introduction-to-brief-binary-robust-independent-elementary-features-436f4a31a0e6

BRIEF는 2010년 calonder가 소개한 이진 기술자로

두 점을 가우시안 분포로 생성하여, 비교 쌍 256개를 만듦 -> 크기가 256비트

고정된 크기의 가우시안 분포에서 비교쌍을 생성하므로 스케일, 회전 변환 대처 불가

ORB Oriented FAST and Rotated BRIEF

ref : medium.com/data-breach/introduction-to-orb-oriented-fast-and-rotated-brief-4220e8ec40cf

2011년 OpenCV 연구소의 Rublee가 소개한 고속 특징 검출기로

FAST 키포인트 검출기와 수정 BRIEF 기술자를 기반으로 만들어진 알고리즘.

키포인트 주방향으로 회전시킨 BRIEF 기술자를 사용하여 회전 변환에도 불변함. 크기는 512비트

BRISK: Binary Robust Invariant Scalable Keypoints

ref : gilscvblog.com/2013/11/08/a-tutorial-on-binary-descriptors-part-4-the-brisk-descriptor/

2011년 Leutenegger가 소개한 회전, 스케일 변화에도 강인한 이진 특징 기술자.

특징점 주위 60개 점을 비교 쌍으로 사용하는데,

특징 스케일에 따른 거리 조건을 만족하는 쌍만 선정하여 스케일에 강인해짐

+ 특징점 방향에 따라 회전한 60개 점을 사용해 회전 불변

크기는 512비트

이진 기술자 binary descriptor의 필요성

이전에 살펴본 SIFT, PCA-SIFT, GLOH 특징 벡터(특징 기술자)들은

각각 128, 20, 128차원으로 여전히 매칭, 물체 추적을 수행하기에는 차원수가 너무 크고

SIFT 키포인트의 특징 벡터를 실수로 표현하는 경우 4바이트(float) x 128(개) = 512바이트가 필요.

기존 키포인트로 매칭하기에는 키포인트 간 거리 계산시 계산량이 너무 많아짐.

이진 기술자와 조사 패턴

2012 Heinly는 특징점 중심으로 조사 패턴을 이용해 이진열을 만드는 방법을 제안함.

특징점 주위 존재 하는 두 화소를 비교할 쌍으로 보고, 명암값을 비교해 이진 값을 생성

특징점 주위 수백 개의 쌍을 검사 -> 수백 비트의 이진열 binary string 생성

* 아래 그림은 세 비교쌍으로 이진열을 생성하는 과정을 보임

이진 특징 기술자를 구하는 방법

ref :medium.com/@ulasmezin/brief-descriptor-binary-robust-independent-elementary-features-493d89ea656d

위에서 설명한 이진 열은 이진 특징 기술자라고 할수 있으며 0, 1의 값을 갖는 이진 수로 이루어짐.

이진 특징 기술자들은 크기가 128, 256, 512 등이 될수 있으며

SIFT가 512바이트 크기를 차지했던것과 비교해,

128개로 이루어진 이진 특징 기술자는 128비트 정도만 공간을 차지함.

구하는 방법은 키포인트 중심으로 S x S 사이즈의 이미지 패치(조사 패턴)을 놓고

조사 패턴에 연결된 쌍끼리 값을 비교하여 구하면 되겠다.

아래의 이진 검사 방법을 보면 p(x)와 p(y)를 비교하는데, 각각 조사 패턴으로 연결된 점 x와 점 y의 강도를 말한다.

점 y의 명암 값이 크다면 조사 결과는 1이되고, x값이 크다면 조사 결과는 0이 된다.

이미지 패치 p에 비교 쌍(조사 쌍)의 갯수만큼이 이진 특징 백터의 크기가 되겠다.

조사 쌍들의 예시

이진 특징 기술자를 얻으려면 키포인트 주위를 검사할 조사 쌍이 필요한데,

아래 그림들 다양한 옵션을 주면서 만든 조사쌍들이며, 특정 확률 분포와 관련이 있음

G I는 점 X와 점 Y 각각을 균일하게 선정하여 연결시킨 경우

G II는 점 X, Y를 가우시안 분포에 따라 임의로 선정하여 연결.

G III에서는 X와 Y의 쌍이 가우시안 분포를 따르도록 선택 되었는데.

    여기서 x는 0.04 * sigma2를 표준편차로 하는 x를 선정하고,

    점 y는 점 x의 평균과 표준편차 0.01 *sigma2에 있는것을 선정

G IV는 원형 그리드 내부에 존재하는 점 X와 점 Y를 임의로 선택하여 조사쌍 들을 생성

PCA-SIFT

대부분 동일하나 특징 벡터 x를 추출하는 과정이 다름.

키포인트 중심으로 옥타브 o, sigma_o 영상에서 주 방향으로 39 x 39 윈도우 적용

윈도우 내부 d_y, d_x 영상 취득

=> 39 x 39 x 2 = 3,042차원 벡터 취득

이 고차원 벡터를 d = 20차원으로 축소 하여 특징 벡터 x로 사용.

SIFT와 PCA-SIFT의 비교

키포인트를 중심으로

기본 SIFT : 주 방향으로 4 x 4 윈도우, 8방향 그라디언트 히스토그램으로 4 x 4 x 8 = 128차원

PCA-SIFT : 주 방향 39 x 39 윈도우, dy, dx영상으로 39 x 39 x 2 = 3,042차원 + PCA 수행하여 d=20차원으로 축소

2004 ke에 따르면 PCA-SIFT는 SIFT에 근접한 반복력을 가지며, 보다 고속 매칭이 가능(128 -> 20차원)

GLOH Gradient Loation Orientation Histogram

SIFT, PCA-SIFT와 같은 특징은 정사각형 윈도우로부터 키포인트 기술자를 검출해냄.

GLOH은 정사각형 대신 원형 윈도우 사용

옥타브 o의 sigma_o 영상의 키포인트를 중심으로

우측 아래와 같은 3원으로 17개 영역으로 분할. 각 영역은 16단계 그라디언트 방향 히스토그램 계산

=> 17 x 16 = 272차원 특징백터 + PCA로 128차원으로 축소

128차원 특징벡터 x를 취득

SIFT 특징

키포인트라 부르며, 위치와 스케일 정보를 가짐 (y, x, sigma)

-> sigma를 이용하여 크기 변환에 대응 가능

기술자 추출을 위한 윈도우 크기를 sigma에 따라 조절하거나, 스무딩이 필요

SIFT 기술자 추출 위치

SIFT 특징은 피라미드 구조

키포인트가 옥타브 1의 3번째 영상(sigma=2.5398)에서 검출된 경우.

옥타브 o = 1, sigma_o = 2.5398로

SIFT 기술자는 o번 옥타브, sigma_o 영상에서 기술자 추출

회전 변환애 대응하기 위한 주 방향 탐색

이미지 회전에 대응하기 위해 윈도우 방향 조절이 필요.

-> SIFT 기술자 추출전 주 방향 dominant orientation을 탐색

1. 키 포포인트를 중심으로 일정 크기 윈도우를 씌움

2. 윈도우 내 화소 집합으로 그라디언트 방향 히스토그램 취득

* 그라디언트 방향은 10도 간격으로 양자화, 36개 구간을 가진 히스토그램

3. 그라디언트 방향 히스토그램 계산시 그라디언트 크기를 가중치로 사용하며,

가우시안을 씌워 멀어질수록 적은 가중치 방영되도록 함.

* 아래 그림은 그라디언트 방향 히스토그램 계산을 위해 가우시안 블러링된 이미지에 방향 강도를 나타낸 영상

4. 히스토그램에서 가장 큰 값을 가진 방향을 주 방향으로 사용.

* 최고 값의 0.8배 이상인 방향이 존재할 경우 해당 방향도 주방향으로 판단하여 새 키포인트 생성.

 => 위치는 같지만 방향이 다른 여러 키포인트가 생성 될 수 있음.

* 키포인트 정보 : 위치, 스케일, 주 방향 (y, x, sigma, theta)를 가짐.

* 아래는 위 이미지에 대해 주방향 취득을 위한 그라디언트 히스토그램

주방향을 이용한 SIFT 기술자 추출

키포인트에 적절한 크기의 회전된 4 x 4윈도우를 씌움.

이때 윈도우는 주방향 theta가 기준되도록 회전

해당 키포인트의 그라디언트 방향을 계산 후,

8단계로 양자화 된 그래디언트 방향 히스토그램을 구함 

주방향 탐색때 처럼 회전된 윈도우 내부의 그라디언트 크기를 가중치로, 가우시안 블러링을 적용함.

하나의 키포인트 기술자는 4 x 4 x 8 = 128차원의 특징벡터 x로 추출됨

광도에 불변한 SIFT 기술자

1. 키포인트 기술자 특징 벡터 x를 벡터의 크기(노름)로 ||x||로 나누어 단위 벡터로 변환

2. 단위 벡터에 0.2보다 큰 요소가 존재시(상한 0.2), 0.2로 변경 후 다시 단위 벡터로 변환

=> 스케일, 회전, 광도 불변한 128차원 키포인트, 특징벡터 x 완성

위 과정을 거쳐 구한 SIFT 특징은

(y, x, sigma, theta, v_x)로 정리할수 있으며,

이 키포인트 특징 집합이 매칭 연산의 입력으로 사용되어, 두 영상 사이 매칭 쌍을 찾는데 사용

opencv에서 SIFT

sift = cv.SIFT_create()
kp, des = sift.detectAndCompute(gray,None)

sift 객체를 생성 후

sift.detectAndCompute(명암 영상,None)으로

키포인트들과 키포인트의 기술자들을 반환 반음.

키포인트 기술자들은 num of keypoints x 128 차원의 형태로 반환됨

docs.opencv.org/master/da/df5/tutorial_py_sift_intro.html

특징 기술자 feature descriptor의 조건

특징을 매칭, 인식 등에 사용하기 위해선

다음 조건 충족이 필요

1. 기술자 분별력이 커야 함.

완전히 서로 다른 두 영상이 주어질 때, 각 영상에서 구한 기술자들은 달라야 함

완전히 다른 두 영상 끼리는 매칭 될 수 없으므로.

2. 여러 변환에 불변해야함

평행 이동, 회전, 크기, 스케일, 비틀림 변환 등에도

특징 기술자가 변하지 않아야 매칭을 할 수 있음

3. 추가적으로 특징 기술자는

위와 같은 기하 불변성 geometry invariant 뿐만 하니라 광도 불변성 photometric invariant을 가져야 함.

4. 특징 기술자의 크기(차원)이 작을수록 좋음.

매칭은 기술자 간 거리로 판단하므로, 차원이 클수록 계산량이 많아짐

앞서 살펴본 관심점들

모라벡, 해리스 코너 알고리즘은 (y, x)

해리스 라플라스, SIFT, SURF 등의 특징은 (y, x, sigma)로 표현

특징, 관심점으로부터 기술자 추출하기

해당 특징점을 중심으로 윈도우를 씌우고, 보아야 함.

-> 윈도우 모양, 크기, 살펴볼 주제를 선택하여야 함.

카메라가 이동하여 찍은 영상의 경우 -> 쉽게 매칭 성공

영상이 이동 + 회전 변환이 수행된 경우 -> 크기, 회전 변환에 불변한 기술자 사용해야함

영상에 조명변화나 가림이 생기는 경우 -> 기하, 광도 변환에 불변한 기술자 사용 필요

그래프 기초

그래프 G = (노드 V, 간선 E)로 정의

이미지의 그래프화

이미지를 그래프로 표한하면 픽셀 하나가 하나의 노드

서로 다른 두 노드 v_p, v_q를 연결하는 에지는 가중치 w_pq를 가짐(무방향 그래프)

여기서 가중치 w_pq는 두 노드간 유사도나 거리를 의미

함수 f(v)가 노드의 명암을 구하는 함수면, 명암 영상에서의 거리와 유사도는 아래와 같이 구할수 있음

명암 이미지를 그래프로 표현하기

아래의 그림은 입력 명암 영상이지만 명암 차를 에지로 본다면 그래프로 볼 수 있음.

유사도가 높은 경우 같은 연결 요소, 영역에 속한것이고,

유사도가 낮은 경우 다른 연결요소, 영역에 속한것으로 볼 수 있음.

그래프 알고리즘을 통한 영역 분할

그래프 알고리즘은 지역 최적해가 아닌 전역적인 최적해를 구하여야 하므로

전역적으로 최적해가 아니라면 분할선으로 판단해선 안됨.

그래프 영역 분할 고려 사항 2가지

1. 목적 함수

2. 목적 함수로 최적해를 찾는 효율적인 탐색 알고리즘

최소 신장 트리를 이용한 영역 분할

우선 신장 트리 spanning tree란 모든 노드를 연결하면서 트리 조건을 만족하는 그래프

최소 신장 트리 Minimal Spanning Tree MST는 간선(에지)의 가중치 합이 최소인 신장트리

다음의 입력 영상과 연결 요소 C = {v1, v6, v7, v11, v12}가 주어질때

최소 신장 트리 MST(C) = {(v1, v6), (v6, v11), (v11, v12), (v12, v7)}

연결 요소의 균일 정도는 최소 신장 트리의 가장 큰 가중치로 구할 수 있음

위 경우 intra(C) = 2

최소 신장 트리를 확장하는 경우 v13보다 v8을 추가할때 intra(C) = 2가 되어 균일성이 유지

두 연결 요소의 균일성 비교

연결 요소 C_i, C_j가 주어질때 multi_intra(C_i, C_j)는 균일하지 않으먄 큰 값을 가짐.

diff(C_i, C_j)는 두 연결 요소 사이의 다른 정도를 나타내는 척도

diff(C_i, C_j) > multi_intra(C_i, C_j)으로 참이면 연결요소가 적절하게 분할된 상태.

위 식에서 tau(C)는 연결 요소 간의 차이 diff()와 연결 요소의 균일성 intra(C) 사이 차이를 위한 임계값

|C|가 작을 수록 tau(C)는 큰 값을 가지게 되고, multi_intra(C_i, C_j) 또한 커지므로

diff를 더 키워주는 역활. k는 분할 세밀한 정도 조정

위 내용을 정리하면 입력 영상 f가 r개 연결 요소로 분할 된 경우

D(C_i, C_j) = true 인경우 적절히 분할되었음을 의미하며, 더이상 분할되지 않음.

최소 신장트리 이용한 영상 분할

1. 거리를 가중치로 갖는 그래프 생성

2. 에지를 오름차순 정렬 

3. 초기 분할 수행(한 픽셀이 하나의 연결 요소로 다룸.)

4. 모든 에지에 대해 반복

 - i 번째 에지 e = (v_p, v_q)

 - S_i-1에서 v_p와 v_q가 속한 연결요소를 C_p, C_q라 정의

 - C_p != C_q이며, diff(C_p, C_q) <= multi_intra(C_p, C_q)인 경우

  => C_p와 C_q를 합쳐 하나의 연결 요소 만들어 S_i로 

 ** 두 연결요소간의 거리 <= 두 연결요소 간의 균일성 

       ==>두 연결 요소간의 균일성보다 거리가 가깝다 =>하나의 연결요소로 판단

 - 위 조건이 아닌 경우 S_i = S_i-1

최소 신장 트리를 이용한 영상 분할 예시

분할에서 사람과 컴퓨터의 차이

사람은 무의식적으로 물체에 대한 지식과 의도로 분할해서 볼수 있음

컴퓨터에서 분할은 인식을 하기 위해 전처리로 수행하는 작업

에지, 특징을 통한 영상 분할의 한계

에지를 통한 영상 분할 -> 완전한 폐곡선이 필요하지만 그렇지 않은 경우가 많음

컴퓨터 비전에서의 영역. 물체를 나타내는 연결된 화소 집합

-> 모양, 섹상, 질감 정보로 특징 벡터, 기술자를 추출할수 있어야함.

특징점은 반복적으로 검출될수 있는 하나의 점일 뿐이며, 그 점 주위 픽셀로 기술자 추출하나 영역을 구하기엔 부족

임계화를 통한 영역 분할

대표적으로 클래스내 분산을 최소화 클래스간 분산을 최대화 하는 임계점을 찾는 오츠 이진화 알고리즘

주위 픽셀값을 이용하여 임계치를 적용하는 적응적 임계화 방법 등이 있음

* 적응적 임계화 알고리즘 성능 비교 trier 95

군집화를 이용한 영역  분할

아래는 대표적인 군집화 알고리즘인 k-means로 구한 결과

컬러 영상을 3차원 공간에 맵핑하여 k means 수행

SIFT의 한계

SIFT는 좋은 성능을 보이는 특징 검출 알고리즘이지만

bay2006에 따르면

SIFT는 800 x 640 영상에서 400ms

해리스 라플라스는 2100ms가 소요됨.

bay는 2006년 SIFT보다 5~6배 정도 더 빠르게 특징들을 검출할수 있는 SURF를 소개

SURF 개요

SURF는 헤시안 행렬식을 사용.

sigma를 조금씩 증가시켜 3차원 스케일 공간을 만들고, 지역 극점을 찾아 특징점으로 사용.

SURF가 이전 방법과 다른 점은 행렬식을 근사화 하여 사용한다는 점임.

일단 위 해시안 행렬의 원소들은 아래와 같이 정의

d_yy는 sigma 가우시안 스무딩 적용 후 y방향으로 두번 미분하여 구한 영상

이는 y방향으로 2번 미분한 가우시안 마스크를 컨벌루션한것과 같은 결과를 가짐

근사화된 가우시안 마스크 활용

아래의 그림에서 위의것은 가우시안 마스크를 y방향으로 2번 미분하여 구한 마스크(연산자)(1)과

y방향으로 1번 x방향으로 1번 미분하여 구한 마스크(연산자)(2)임

* 가우시안 연산자를 x방향으로 2번 미분한 연산자는 y방향을 2번 미분한것을 90도 회전하여 구할수있음.

아래 그림은 가우시안 마스크를 2번 미분한 연산자를 근사화하여 구한 연산자임

SURF에서는 아래의 근사화된 마스크 사용.

적분 영상을 통한 덧셈 연산 최소화

추가적으로 SURF는 D_yy를 빠르게 계산할수 있도록 적분 영상 integral image 사용

D_yy를 구하기 위해 일반 영상을 사용하는 경우 a_1을 구하는데만 14번 덧셈을 수행해야 함.

적분 영상의 경우 a_1 뿐만 아니라 블록의 크기와 무관하게 세 번의 덧셈 만으로 블록 함 계산 가능.

다중 영상 취득을 위한 다중 스케일 연산자 활용

SIFT에서는 단일 스케일 연산자로 다중 스케일 영상을 획득하였었음.

SURF는 단일 스케일 영상에 그러니까 원본 영상에 다중 스케일 연산자 사용하여 옥타브 1개를 만듬.

옥타브 0의 경우 :  9 x 9, 15 x 15, 21 x 21, 27 x 27 크기의 연산자 사용.

SIFT 개요

이동, 회전, 스케일 불변한 대표적인 특징 검출 알고리즘으로

SIFT Scale-Invariant Feature Tranform(Lowe99)

SIFT 역시 스케일 공간을 다루면서, 피라미드 구조로 됨.

피라미드로 원본 영상이 4 x 4가 될때까지 줄임

한 층은 스케일 공간 상 6개의 영상으로 구성(옥타브)

원본 크기의 영상들을 옥타브 0, 다음은 옥타브 1, ...

sigma_1 = 1.6

옥타브 2 - sigma_2 = k * sigma_1

...

옥타브 i+1 - sigma_i+1 = k * sigma_i의 규칙을 따름

이미지 피라미드

한 옥타브에서 6개 영상 구하는 방법

i번째 영상은 sigma_i로 스무딩이 되어있음

i + 1번쨰 영상은

원본 영상을 sigma_i+1로 스무딩 = i 번째 영상을 sigma_i+1와  sigma_i의 차이(sigma 제곱 차 루트)로 스무딩

나머지 옥타브 영상 구하는 방법

1. 이전 옥타브의 네 번째 영상을 다운 샘플링하여 새 옥타브의 첫번째 영상으로 사용.

2. 위 sigma 차이를 이용한 방법으로 옥타브의 나머지 5개 영상 획득

3. 영상의 크기가 4 x 4인 옥타브가 만들어질떄까지 1, 2반복

SIFT 키포인트 검출하기

계산량을 줄이기 위해 해리스 라플라스 방법에서 보았던 정규 라플라시안을 사용하기 보다는

정규 라플라시안과 유사한 결과를 얻을수 있는 DOG(Difference of Gaussian)를 사용.

DOG는 가우시안 스무딩된 영상의 차로 구할 수 있음.

기존의 가우시안 영상 간의 차 연산으로 DOG 피라미드를 구함.

DOG 피라미드 상에서 이웃한 26개 점 사이에 자신이 극점인 경우 특징점이라 부르고

이 특징점이 임계치를 넘긴다면 키포인트 keypoint라 부름

위 과정을 통해 구한 특징점은 y, x, o, i 정보를 가짐. (o : 옥타브 번호, i : dog 번호)

이제 옥타브 0영상으로 변환해야하고, o와 i에 대한 정보가 스케일값 s로 변환해야 하므로 아래와 같이 구할 수 있음.