728x90
이전 부터 인공 지능에 대해 무크 사이트에서 공개 강의로 올라와 있는건 알고 있었지만
그 동안 볼때마다 확률, 통계, 공업 수학 등 이론적 배경이 부족하다 보니 이해하는데 어려움이 많았었다.
그래서 전에는 포기하고 제대로 보지 않았는데
오늘 네이버 메일로 이 강의가 다시 와있더라
kaist.edwith.org/machinelearning1_17/lecture/40603/
그 동안 배경 이론들을 많이 연습했으니 이제 볼수 있을것 같아 한번 보았다.
머신 러닝 기법 응용사례로
스팸 메일 여부, 주가 예측, 헬기 제어 등을 보여주더라
머신러닝 분야
- 지도 학습 : 인스턴스 별 결과, 라벨을 아는 경우 머신 러닝
- 비 지도 학습 : 인스턴스 별 결과, 라벨이 주어지지 않는 경우의 머신 러닝
- 강화 학습 : 목표가 있으나 어떻게 목표에 도달하는지에 대한 정보가 없는 경우의 머신러닝
지도 학습 supervised learning
- 실제 결과를 알고 있는 문제를 학습하는 경우
- 예시
- 스팸 필터링
- 자동 물품 카테고리 분류
- 분류 classification와 회귀 regrssion
- 참 거짓 맞추기 Hit or Miss : 양성, 음성 분류하기
- 점수 매기기 Ranking : A+, B, C, F중 무엇을 받았을까?
- 값 예측 value prediction : 물품의 가격 예측하기
비지도 학습 unsupervised learning
- 결과를 주어지지 않고, 주어진 데이터만으로 학습하는 문제
- 비지도 학습 예시
- 군집 찾기 cluster
- 숨겨진 인자(요소) latent factor 찾기
- 그래프 구조 찾기
- 클러스터, 필터링,
- 텍스트 데이터로부터 주제 단어 찾기
- 얼굴 데이터로부터 latent 중심 이미지 찾기
- 궤적 뎅이터에서 노이즈 필터링 하기
압정 문제 Thumbtack Question
- 압정을 던졌을 때 기울어져 있을까? 뒤집혀 있을까?
- 동전은 앞뒷면이 동일하니 50:50이지만 압정은 다른 결과가 나올것임
- 5번 던졌을때, 3번은 뒤집혀 있었고(핀이 위), 2번은 기울어 져있었(머리가 위)다고 하자.
=> 시행 결과 핀이 위일 확률은 3/5, 머리가 위일 확률을 2/5
이항 분포
- 이산 확률 분포중 하나로 상호 배반 사건만 존재하는 시행들(베르누이 시행)으로 나타나는 확률 분포
- 압정 던지기는 iid 라는 가정을 함. 독립적(independent)이고, 동일한(identically distributied) 확률 분포를 가짐.
- 데이터 D = H, H, T, H, T로 주어질때,
- n = 5
- k = a_H - 3
- p = theta(H가 나올 확률)
- P(D | theta) = theta^(a_H) (1 - theta)^(a_T) : theta 가 주어졌을때, D가 관측될 확률
- 이항 분포의 PMF : f(k; n, p) = P(K = k)=
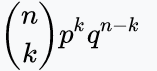
최대 가능도 추정 Maximum Likelihood Estimation
- P(D | theta) = theta^(a_H) (1 - theta)^(a_T)
- 우리의 가정 : 압정 던지기 결과는 theta 확률의 이항 분포를 따른다.
- 어떻게 theta를 설정할때 가장 이 데이터를 가장 잘 설명을 할수 있을까?
- 관측 결과를 가장 잘 나타내는 분포를 찾아야 한다.
- 최적의 theta를 구하여야 한다. 어떻게 theta를 구할까?
- 최대 가능도 추정 : 관측된 데이터들의 확률을 최대화 하는 theta를 찾는 방법
- hat{theta} = argmax_{theta} P(D|theta)
- 위 압정 시행을 통해 추정한 hat{theta} = a_H/(a_t + a_H)
시행 횟수와 에러 구간
- 추가적인 시행은 추정 오차를 줄여주게 된다.
- 추정 모수 hat{theta}, 진짜 모수 theta^*라고 할때
- Hoeffding의 부등식에 따르면 다음의 확률 상한을 얻을 수 있음.
- 시행 횟수가 늘어날수록 실제 오차와 추정 오차 간격이 줄어듦.
- P(|hat{theta} - theta^*| >= e) <= 2 e^{2Ne^2}
- 이것은 PAC(Probably Approximate Correct) learning
- 추정량 hat{theta}는 위 확률 범위와 오차 범위 내에서 올바름
베이즈와 사전 확률
- 사전 정보를 파라미터 추정 과정에 반영 할수 있음(사전 확률)
- 사전 정보를 가미한 추정량을 구하자
- P(theta | D)
Posterior= P(D|theta)Likelihoodx P(theta)Prior/ P(D)Normalizing Constant- 이전에 P(D|theta)는 정의하였음.
- P(D | theta) = theta^(a_H) (1 - theta)^(a_T)
- 50:50이 사전 확률 P(theta)로 사용 될 수 있음.
- 사전 확률과 데이터를 반영한 P(theta | D)를 구해보자
베이즈 관점에서 살펴보기
- P(theta | D) 비례 P(D | theta) P(theta)
- P(D | theta) = theta^(a_H) (1 - theta)^(a_T)
- P(theta) = ????
- 가능도 P(D | theta)가 이항분포를 이용하여 구한것 처럼 P(theta)도 확률 분포를 이용하여 구할 수 있다!!
- 베타 분포로 사전 확률을 사용하자.
- 베타 분포의 확률 밀도 함수 P(theta) (이항 분포에서 앞면, 뒷면 횟수로 가능도를 구한것 처럼, alpha와 beta가 필요)
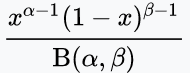
- 사후확률 P(theta | D)를 정리하면..
- P(theta | D) 비례 P(D | theta) P(theta) 비례 theta^(a_H) (1 - theta)^(a_T) theta^{alpha -1} (1 - theta)^{beta -1} = theta^{a_h + alpha - 1} (1 - theta)^{a_t + beta - 1}
베타 분포로 사전 확률을 사용하자.
사후확률 최대화 MAP Maximum A Posterior
- MLE에서는 가능도 P(D | theta)를 최대화 하는 추정량 theta를 구하였었다.
- hat{theta} = argmax_{theta} P(D | theta)
- hat{theta} = a_h/(a_h + a_t)
- MAP는 가능도가 아닌 사후확률을 최대화 하는 추정량 theta를 구하는 방법
- P(theta | D) 비례 thet^{a_h + alpha - 1} (1 - theta)^{a_t + beta - 1}
- hat{theta} = (a_H + alpha - 1) / (a_h + alpha + a_t + beta - 2)
- MLE에는 사전 확률을 반영할수 없으나 MAP는 사전확률을 반영할수 있게 된다!!
300x250
'인공지능' 카테고리의 다른 글
| [인공지능및기계학습]02.3 결정 트리 개요 (0) | 2021.01.13 |
|---|---|
| [인공지능및기계학습]02.머신러닝의 기반들 (0) | 2021.01.08 |
| 컴퓨터 비전 & 패턴 인식 - 32. 아웃라이어에 대처하는 기하 변환 방법 (0) | 2020.12.16 |
| 컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법 (0) | 2020.12.16 |
| 컴퓨터 비전 & 패턴 인식 - 30. kd트리 기반 최근접 이웃 탐색 (0) | 2020.12.16 |