728x90
아웃라이어의 영향을 제거하거나 약화시키는 방법이 필요
-> M 추정, 최소 제곱 중앙법이 있음
최소제곱법으로 구한 추정량을 아래와 같이 정의할때
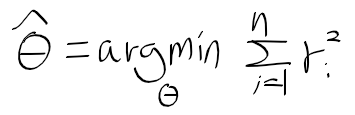
M 추정 M estimator
m 추정을 활용한 식은 아래와 같음.
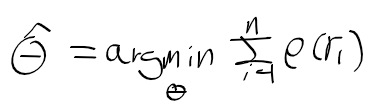
rho(r_i) = r_i^2이면 최소제곱법과 동일.
하지만 r_i가 일정 값 이상(오차가 크다면)이면 함수의 크기를 줄임.
이때 함수 rho()는 huber 함수로,
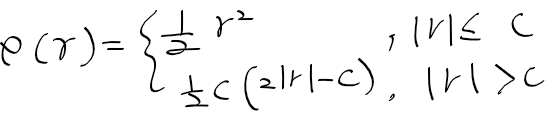
r이 임계값보다 작은 경우 2차 곡선 사용.(오차가 작으므로)
r이 임계값보다 큰경우 1차 곡선을 사용하여 오차의 영향력을 보다 줄임(오차가 크므로)
최소 제곱 중앙값 LMeds: Least median of Squared
최소 제곱 중앙값을 활용한 식은 아래와 같음.

n개의 특징점 중 중앙값을 취함.
중앙값인 매칭쌍의 오차를 최소로 하는 기하 변환 행렬 T의 매개변수들을 찾는 방법
붕괴점 breakdown point
더 이상 추정 알고리즘이 동작하지 않는 아웃라이어 비율.
최소제곱법은 붕괴점이 0%
최소제곱중앙값은 50%
RANSAC을 이용한 기하변환 추정
입력 : 대응쌍 집합 X, 반복 회수, 인라이어 판단 임계치 t, 인라이어 집합 크기 d, 적합오차 e
출력 : 기하 번환 행렬 T
Q = []
for i in range(k):
X에서 임의의 대응쌍 3개 선택.
세 대응쌍으로 최소제곱법으로 T_j 추정
세 대응쌍은 인라이어로 판단
m = X에서 세 대응쌍을 제외한 대응쌍 집합)
for p in m:
# T_j로 첫번째 대응쌍 요소를 변환시킨 p.1'와 p.2의 오차가 t보다 작은경우
# 인라이어로 판단
if (p.2 - T_j*p.1) < e:
p를 인라이어에 추가
# 인라이어의 개수가 d이상이 되면
if |inlier| >= d:
인라이어 요소(대응쌍)들로 새 T_j 계산
# 구한 T_j의 적합 오차가 e보다 작은경우 Q에 추가
if T_j 적합 오차 < e:
T_j를 Q에 추가
Q에 있는 것들 중에서 가장 좋은 변환행렬 T를 선정
300x250
'인공지능' 카테고리의 다른 글
| [인공지능및기계학습]02.머신러닝의 기반들 (0) | 2021.01.08 |
|---|---|
| [인공지능및기계학습]01.동기부여 및 기초 (0) | 2021.01.07 |
| 컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법 (0) | 2020.12.16 |
| 컴퓨터 비전 & 패턴 인식 - 30. kd트리 기반 최근접 이웃 탐색 (0) | 2020.12.16 |
| 컴퓨터 비전 & 패턴 인식 - 29. 이미지 매칭을 위한 거리 척도와 매칭 방법 (0) | 2020.12.16 |