728x90
목표
- 머신러닝의 고전적 방법들을 배워보자
- 규칙 기반 방식 rule based approach
- 고전 통계적 방식 classical statisitc approach
- 정보 이론 방식 information theory approach
- 규칙 기반 머신러닝
- 어떻게 특성화되거나 일반화 할수 있는 규칙을 찾는지 알아보자
- 왜 이러한 규칙이 쉽게 깨지는지 알아보자
- 결정 트리
- 어떻게 훈련 데이터셋으로 결정 트리를 만들어낼까
- 왜 새로운 데이터셋에 대해 트리가 약한 분류기가 될까.
- 선형 회귀
- 어떻게 훈련 데이터셋으로 파라미터를 추론하는가
- 왜 피처 설정이 한계를 가지는가.
규칙 기반의 머신 러닝 rule based machine learning
- 완벽한 세상에서의 규칙 기반의 머신 러닝 : 아래와 같은 가정을 할때
- 관측 에러가 없고, 항상 일관된 관측 결과를 구할 수 있다.
- 관측 결과에 확률적인 영향, 임의에 의한 영향이 존재하지 않다.
- 시스템을 설명할수 있는 모든 정보를 얻었다.
- 사람이 기상을 관측해서 나가서 운동할수 있는지의 여부, 규칙을 이용한 머신러닝으로 판단하자.
- <기상, 온도, 습도, 바람, 수온, 기상 변화> 정보를 얻고, 이 정보로 운동할수 있는지 예측하자.
함수 근사 function appraoximation
- 머신 러닝이란?
- 머신 러닝은 더 나은 근사 함수를 만드는 작업이라 할 수 있다.
- 이전에 정의한 완벽한 세상에서 운동을 할수 있는지의 여부를 다루자.
- 인스턴스 X
- 피처 O : <화창, 따뜻, 보통, 강함, 따뜻, 같음>
- 라벨 Y : <운동 가능>
- 훈련 데이터셋 D
- 인스턴스 관측 집합
- 가설 H
- X로 Y를 얻을수 있는 어떤 함수, 가설들이 존재할까?
- h_i : <화창, 따듯, ?, ?, ?, 같음> -> 운동 가능
- 얼마나 많은 가설이 존재할까?
- 타겟 함수 c
- 피처와 라벨로 알수 없는 타겟 함수. 가설 H의 목표가 되는 함수.
- 인스턴스 X
함수 근사를 시각적으로 살펴보기
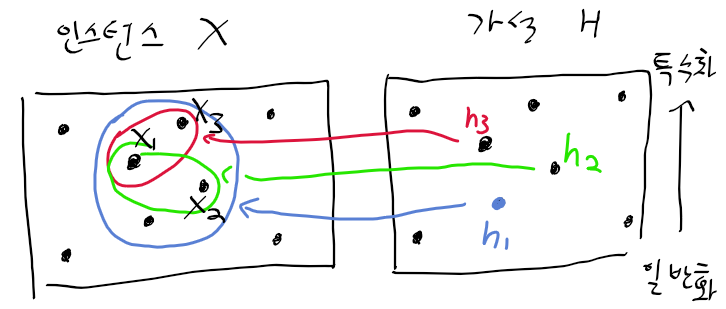
- 다음의 인스턴스 x가 존재할때,
- x1 : <화창, 따뜻, 보통, 강함, 따뜻, 같음>
- x2 : <화창, 따뜻, 보통, 약함, 따뜻, 같음>
- x3 : <화창, 따뜻, 보통, 강함, 따뜻, 변함>
- 아래의 가설 H가 존재한다고 하자
- h1 : <화창, ?, ?, ?, 따뜻, ?> -> 기상이 화창하고, 수온이 따뜻한 경우 -> 운동 가능
- h2 : <화창, ?, ?, ?, 따뜻, 동일> -> 기상이 화창하고, 수온이 따뜻하며, 기상 변화가 없을때 -> 운동 가능
- h3 : <화창, ?, ?, 강함, 따뜻, ?> -> 기상이 화창하고, 바람이 강하며, 수온이 따뜻할 때 -> 운동 가능
- x2를 h3 가설을 기준으로 판별시 -> 운동 불가로 판단.
- x3는 h3 가설을 기준으로 판별 시 -> 운동 가능로 판단.
- 어느것이 가장 나은 함수 근사, 가설이라 할수 있을까?
- 일반화와 특수화에 달린 문제
- 가설 h1은 약한 조건을 가진 가설(일반화 가능한 가설)
- 가설 h3은 강한 조건을 가진 가설
규칙 기반 알고리즘 살펴보기
S 탐색 알고리즘(Find S Algorithm)
최적의 가설 h를 구한다.
데이터셋 D에서 모든 인스턴스 x에 대해
- x가 긍정이라면, 위 예시를 들면 운동 가능하다면
- 모든 피처 f에 대해, 피처와 가설이 동일하면 -> 아무것도 하지 않음.
- ex ) 가설 h3의 기상 특징이 화창, 인스턴스 x_i의 기상 특징이 화창인 경우 아무런 동작을 하지 않음
- 해당 인스턴스 x의 피처 f와 가설의 f가 동일하지 않다면 -> 가설에 포함시킴
- ex ) 가설 h3의 기상 변화특징이 동일, 인스턴스 x_i은 변화인 경우 다르므로 합집합 가설을 구함.
- 모든 피처 f에 대해, 피처와 가설이 동일하면 -> 아무것도 하지 않음.
- x가 긍정이라면, 위 예시를 들면 운동 가능하다면
다음의 인스턴스 x가 주어지고
- x1 : <화창, 따뜻, 일반, 강함, 따뜻, 동일>
- x2 : <화창, 따뜻, 일반, 약함, 따뜻, 동일>
- x4 : <화창, 따뜻, 일반, 강함, 따뜻, 변화>
다음의 가설이 주어지면
- h0 = <0, 0, 0, 0, 0, 0>
- h1 = <화창, 따뜻, 일반, 강함, 따뜻, 동일>
- h_{1, 2, 3} = <화창, 따뜻, 보통, ?, 따뜻, 동일>
- h1에 x2를 반영하면, 바람 특징이 약함(x2), 강함(가설)으로 다름 -> 해당 특징은 ?가 된다.
- h_{1, 2, 3, 4} = {화창, 따뜻, 보통, ?, 따듯, ?}
- x4를 반영하면서 기상 변화 특징이 동일 + 변화 -> ?가 됨.
- 어떤 문제가 존재할까?
- 가능한 가설들이 너무 많아 정리 할수 없음.
- x4를 반영하면서 기상 변화 특징이 동일 + 변화 -> ?가 됨.
버전 공간 version space
- 너무 많은 가설이 존재할 수 있어, 하나의 가설로 모으기가 힘듬
- 특정 가설을 찾기 보다는 범위에 속하는 것을 가설들을 찾아보자
- 가능한 가설 집합 == 버전 공간 : 구간을 정해주자
- 일반 구간 G : 버전 공간의 최대 일반화 가설 집합
- 특정 구간 S : 버전 공간의 최대 특수화 가설 집합
- 버전 공간에 속하는 가설 VS_{H, D}는 일반 구간 G와 특정 구간 S에 속하는 가설들을 갖는다.
- 일반 구간 G : 버전 공간의 최대 일반화 가설 집합
후보자 제거 알고리즘 candidate elimination algorithm
- 버전 공간을 만들기 위해서 가장 일반, 가장 특수한 가설들을 제거해 나가면서 특정 버전 공간을 만드는 알고리즘
- 가장 특수한 가설들을 만들어 주자 -> ex S0 : <0, 0, 0, 0, 0, 0, 0> 무조건 운동 x
- 가장 일반적인 가설 -> ex) G0 : 무조건 나가 운동
- 데이터셋 D의 모든 인스턴스 x를 사용
- x의 라벨 y가 참이라면
- 인스턴스를 품을수 있을 만큼 특수화 된 가설 S를 일반화
- 거짓 이라면
- 일반 가설 G를 특수화.
- 특정 특징이 가장 일반화, 특수화 된 경우가 동일하다면 더이상 특수, 일반화가 불가
- 일반 가설 G를 특수화.
- x의 라벨 y가 참이라면
이게 잘 동작하는가?
후보자 제거 알고리즘으로 올바른 가설들을 구할수 있는가?
- 수렴하는가? -> 가설을 구할수 있어야 한다.
- 올바른가? -> 관측하여 얻은 가설은 참이어야 한다.
다음의 가설이 주어진다면, 잘 동작한다고 할 수 있다.
- 관측 오차와 관측 불일관성이 존재하지 않고,
- 임의 오차가 존재하지 않고
- 모든 관측 정보로 시스템을 예측할수 있는 경우
하지만 위 가정을 할 수 있는 완벽한 세상은 존재하지 않는다.
- 데이터 셋 D의 x인스턴스의 어느 특징에든 노이즈를 가지고 있고,
- 노이즈로 인해 올바른 가설이 제거될수도 있어 올바르게 동작한다고 할 수 없다.
이러한 규칙 기반 머신 러닝 기법의 한계로 노이즈에 강인한 결정 트리가 나옴
300x250
'인공지능' 카테고리의 다른 글
| [인공지능및기계학습]02.4 엔트로피와 정보 이론 (0) | 2021.01.14 |
|---|---|
| [인공지능및기계학습]02.3 결정 트리 개요 (0) | 2021.01.13 |
| [인공지능및기계학습]01.동기부여 및 기초 (0) | 2021.01.07 |
| 컴퓨터 비전 & 패턴 인식 - 32. 아웃라이어에 대처하는 기하 변환 방법 (0) | 2020.12.16 |
| 컴퓨터 비전 & 패턴 인식 - 31. 기하 변환과 최소 제곱법 (0) | 2020.12.16 |