집밖은 위험해

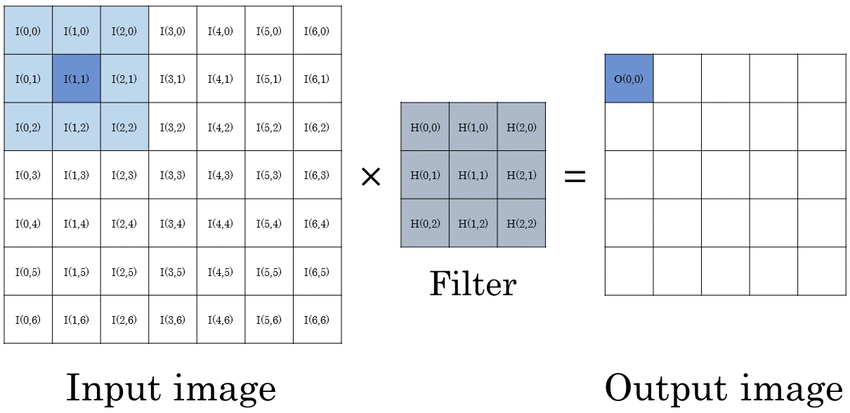
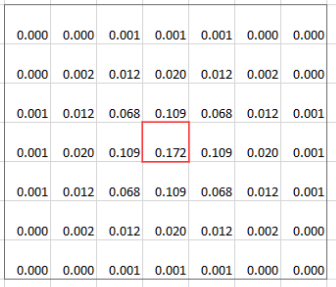
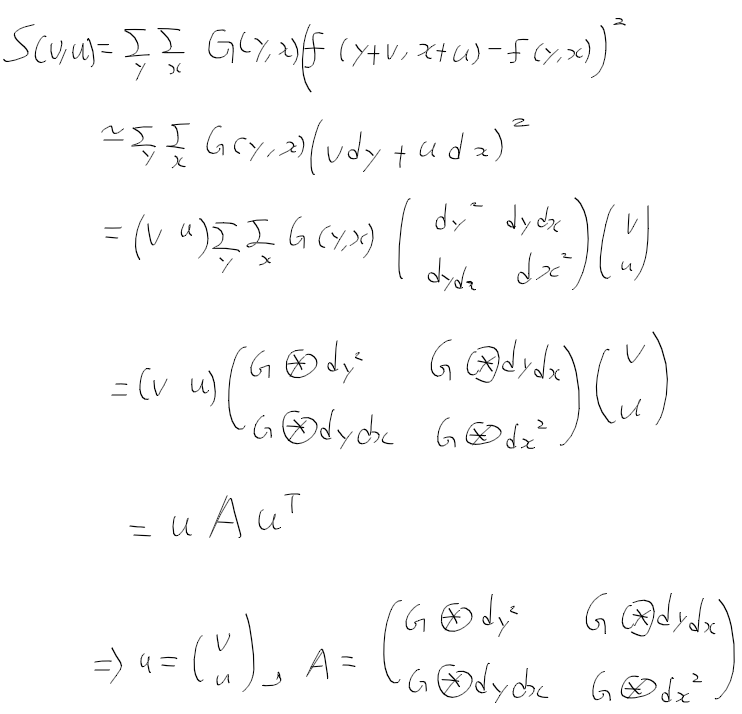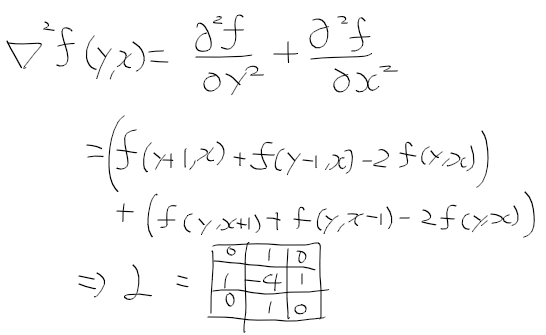정규 라플라시안

지난 글에서는

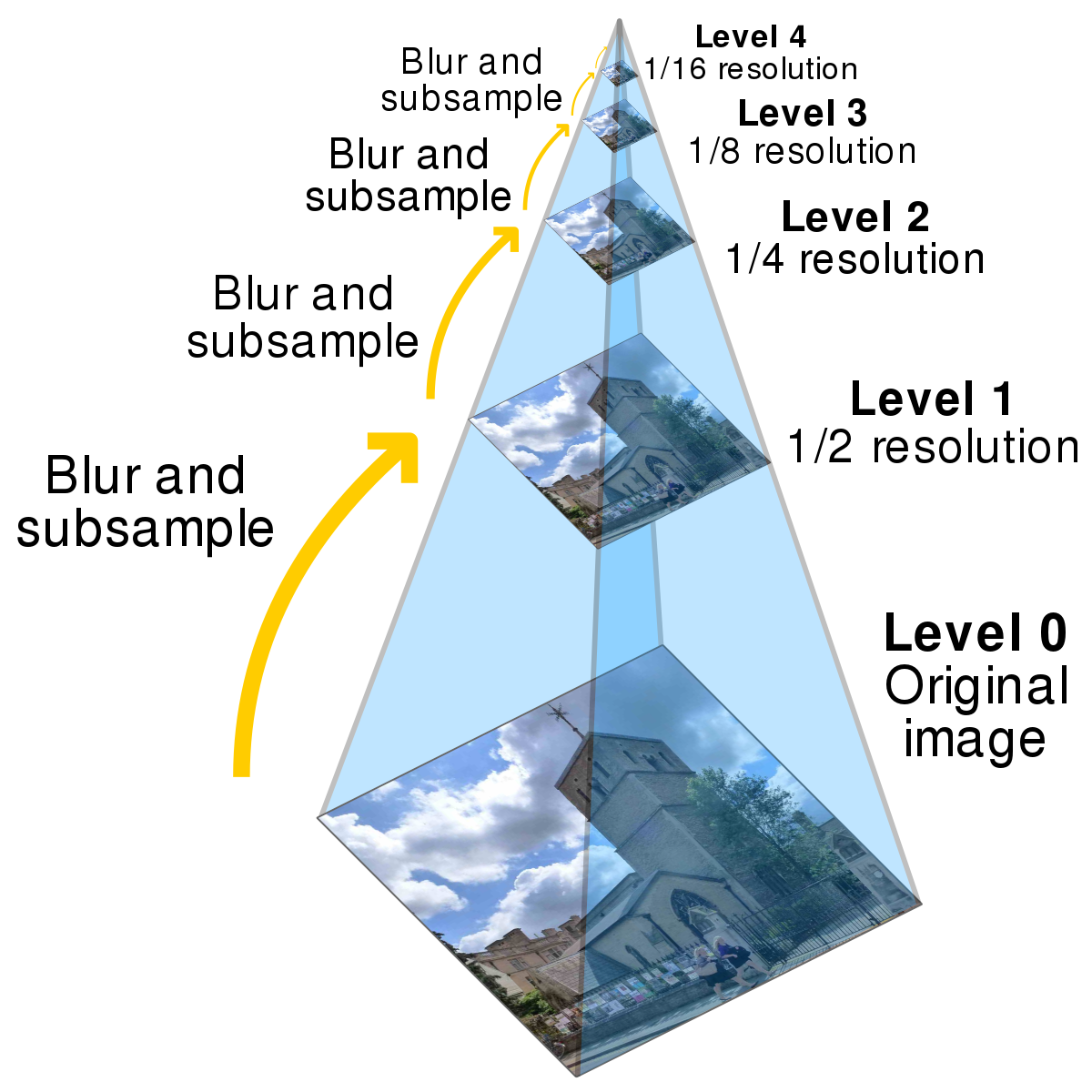
스케일 불변한 특징점을 구하기에 앞서

다중 스케일 영상을 구하였다.

y, x, sigma2로 이루어진 3차원 공간에서 지역 극점을 구하기 위해 정규 라플라시안을 적용하여보자.

정규 라플라시안 normalized laplacian은 라플라시안 영상에 분산 sigma2를 곱한것으로

(LOG 참고)sigma가 클수록 y, x에 대한 이차 미분 영상이 작아지는것을 정규화 하기 위함.

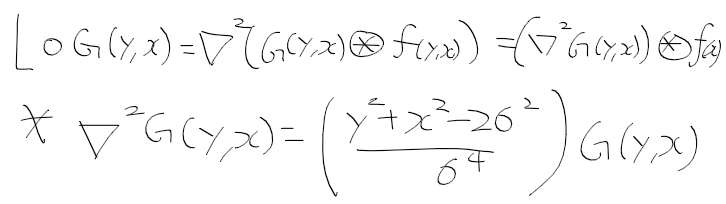
정규 라플라시안은 기존의 라플라시안에 분산을 곱한것이니

다음과 같이 정리할수 있겠다.

린드버그와 스케일 공간

이제 스케일 별화를 다루기 위해 동일하지만 크기가 다른 두 블롭이 존재하는 영상(1)을 살펴보자

원본 영상으로부터 정규 라플라시안 영상을 취득(2)하고,

오른쪽 그래프에서 작은 블롭. 과 큰블롭의 중심에서 스케일 sigma의 변화에 따른 값의 변화를 보여줌 (3)

작은 블롭은 sigma = 3.59에서 극대점, 큰 블롭은 sigma=5.5에서 극대점을 가짐.

(린드버그98)에서 물체 스케일을 s배하는 경우 sigma또한 s배가 된다는 사실을 발견

큰 블롭의 지름(11)/ 작은 블롭의 지름( 7) = 1.57

큰 블롭의 스케일 극대점(5.5)/ 작은 블롭의 스케일 극대점(3.59) = 1.53으로

블롭이 1.5배 커짐에 따라 sigma또한 1.5배 커졌을때 극점을 가지게 됨.

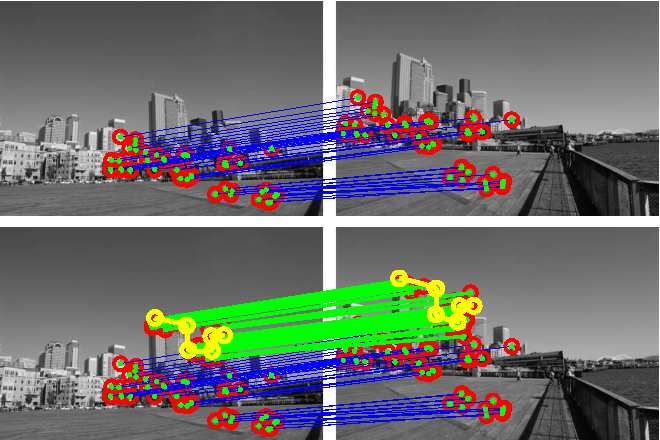
스케일 불변한 특징점의 장점

1. 이동, 회전 불변한 지역 특징의 한계

지난번에 본 특징 검출 방법은 이미지 이동, 회전에 불변한 지역 특징을 검출할 수 있었으나

이미지 크기 변환, 스케일 변화에도 동일한 지역 특징을 검출할수 없는 한계가 있었음.

2. 극복

1) 다중 스케일 공간 y, x, t를 만들고

2) 스케일 변화에 따른 특징의 극점을 구함

이렇게 얻은 극점은 위치 + 스케일 정보를 가짐

=> 이동, 회전, 스케일 불변한 지역 특징

해리스 라플라스 특징 검출

영상 공간 y, x과 스케일 축 t를 분리해서 다룸

영상 공간에는 해리스 코너를

스케일 축에는 정규 라플라시안 적용

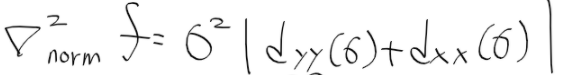
하지만 위 해리스 코너 검출 알고리즘은 단일 스케일에 적용되어, 스케일 방향으로 지역극점을 잘 구하지 못함.

기존의 행렬 A를 스케일 공간 확장을 위해 아래와 같이 수정 후

sigma_D를 변화시키면서 해당 스케일의 특징 가능성 값을 구하고,

지역 특징일 가능성이 높은 (y, x, sigma_i)를 모음.

위 과정으로 다중 스케일 공간에서 특징 가능성 맵으로 지역 특징들을 수집.

(1 단계)

2단계는 스케일 선택 단계

1. 스케일 변화에 따른 지역 극점 sigma_new를 구함.

2. 지역 극점을 못구할시 해당 특징 버림

3. 해당 특징 주변에서 새 극점 y_new, x_new를 찾음

4. 현재 극점과 새 극점이 동일 -> 수렴이므로 최종 특징 선정

5. 현재 극점과 새 극점이 다름 위 연산을 반복

스케일 이론의 필요성

사람은 원본 이미지나 축소한 이미지에서 동일한 특징점을 찾을 수 있다.

하지만 컴퓨터도 산 정상의 사진을 보고 산 꼭대기를 특징점으로 찾을수는 있지만

산 정상만을 확대 시킨 영상에서는 코너가 아닌 수평 에지를 검출함

이런 크기 변환에 불변한 지역 특징을 찾을 방법이 필요

스케일 공간

같은 물체가 서로 다른 영상에서 다른 크기로 나타나는 경우 같은 특징을 구하는 방법은

큰 스케일의 영상에는 큰 연산자, 작은 스케일의 영상에는 작은 연산자를 적용하면 됨.

하지만 영상 스케일을 알 수 없음.

이를 위한 두가지 방법

1. 작은 연산자에서 큰 연산자로 키워가며 여러 스케일 특징 집합을 구함

2. 영상 해상도를 줄여 다중 스케일 영상 구축 후 동일 연산자를 여러 스케일에 적용하여 지역 특징 검출

위 방법의 한계 : 크기 10인 연산자에서 특징 검출시 11, 12, 등에서 검출될 가능성이 높으며 계산 효율이 떨어짐

이와 같은 문제로 스케일 불변 특징을 찾아야 함.

=> 다중 스케일 영상 취득 M을 후, M에서 3 차원의 (y, x, s) 극점을 특정점 집합 F에 취함

다중 스케일 영상 구축 방법

다중 스케일 영상 구축에는 2가지 방법이 존재

첫번째는 가우시안 스무딩을 이용한 방법과 이미지 피라미드를 구축하는 방법

현실에서는 연속적으로 스케일이 변화하나, 피라미드 방식은 스케일이 두배씩 줄어드는 한계를 가져

가우시안 스무딩 방식이 주로 사용됨.

가우시안 스무딩은 표준편차로 스케일 조정하며, 스케일을 키움으로서

물체를 멀리 떨어트려 보는것과 비슷한 효과를 냄

1. 가우시안 스무딩을 이용한 다중 스케일 영상 구축

2. 이미지 피라미드를 이용한 다중 스케일

다중 스케일 영상 

원본 영상에 표준 편차의 값에 따라 가우시안 스무딩을 적용하여 얻을수 있는 영상 집합이 다중 스케일 영상

(y, x, t)를 스케일 공간 scale space라 부르며, t는 스케일 매개변수(t=sigma2)가 된다.

특징 가능성 맵

이미지에 이전에 살펴본

모라벡 알고리즘, 해리스 알고리즘, 해시안 행렬(LOG 필터) 등을 적용하면

특징 가능성 맵을 구할수 있음.

비최대 억제를 통한 지역 특징 검출

특징 가능성 맵을 보면 값들이 다양한 분포를 가지고 있음

이중 지역 최대를 구하고 나머지를 0으로 억제시키는 연산을

비최대 억제라고 부름

하지만 단순 비최대 억제를 적용시 주변 특징들보다 큰 모든 화소들을 검출하므로

주위 보다 일정 비율 커야한다는 조건을 추가 -> 적응적 비최대 억제

이동, 회전 변화에 불변한 특징

위 과정을 통해 구한 지역 특징은

삼각형 영상이 회전 변환을 수행하더라도

지역 특징은 삼각형의 동일한 위치에 관심점, 특징점이 검출되므로 회전 불변함인것을 알 수 있음

대응점 찾기 문제에서 필요한 특징

유사한 두 사진이 주어질때

대응 되는 쌍을 찾으려면 어떻게 해야할까

에지는 물체의 경계에 위치하므로, 독립적으로 구분하기에는 너무 많음

강도와 방향에 대한 정보만 가지고 있어 대응점 매칭에는 부족

1980년대까지는 에지를 연결한 에지 토막을 사용

지역 특징 local feature

비슷한 영상에서도 반복적으로 보이는 특징점을 말함.

위치, 스케일, 방향, 특징 벡터 등의 정보들로 구성됨

지역 특징은 에지의 경우 강도와 방향만 가진것에 비해 많은 정보를 가짐

지역 특징 정보를 얻는 과정은 검출 단계와 기술 단계로 이루어짐

지역 특징 검출에서 위치와 스케일 지역 특징 기술에서는 방향과 특징 벡터를 구함.

검출한 지역 특징들은 위치, 스케일, 방향에 대한 정보를 가짐으로서

위치, 회전, 스케일 변화에 불변해야 함.

대응쌍 검출(매칭 알고리즘)에선 특징 벡터를 비교 -> 거리가 가까운경우 대응점으로 판단.

다른 시점에서의 영상이라 명암은 다를수 밖에없지만 명암 구조는 같음

스케일, 회전, 조명 변화에 무관한 특징 벡터 추출 알고리즘을 구해야 함.

* MB-LBP 특징 벡터의 예시

모라벡 알고리즘

1980년 경 모라벡이 제안한 코너 검출 알고리즘(moravec80)

이미지와 마스크의 제곱차 합을 활용

해리스 코너 알고리즘

1988년 해리스는 노이즈를 제거하기 위해 모라벡 알고리즘에 가우시안 마스크를 적용한

해리스 코너 방법을 발표(Harris88)

위 행렬 A의 고유값을 계산하여 지역 특징, 코너를 구할 수 있음.

1960~ 70년대 에지 검출기

- 소벨 마스크가 주로 사용됨

- 80년대 marr가 2차 미분을 활용한 에지 검출 방법을 제안함.

Marr의 에지 검출

1차 미분 대신 2차 미분 영상을 활용.

미분 전에 가우시안 스무딩으로 잡음을 제거함.

가우시안 스무딩의 표준 편차를 조절함으로서

검출할 에지의 세미한 정도를 조정가능하였음.

라플라시안

2차 미분 영상으로 라플라시안을 사용함

f(y, x)에 대해 y, x방향으로 2차 편도함수를 더한 것이 라플라시안, 라플라시안 영상

아래의 라플라시안 마스크를 영상에 컨볼루션 연산을 수행.

LOG 필터 Laplacian of Gaussian

marr의 에지 검출 방법은 우선 가우시안 스무딩을 적용 하여 노이즈를 제거 후

라플라시안 필터로 2차 미분 영상을 획득하는데

문제는 가우시안을, 라플라시안을 이산 필터로 근사화 하여 구하고, 컨볼루션 연산도 두번 시행하다보니

계산 효율이 좋지 못함.

그래서 아예 가우시안에 라플라시안을 적용한 LOG 필터, LOG 연산자를 사용함.

LOG 필터는 가우시안에 2차 미분을 적용한 것을 이산 필터로 근사화 시킨것으로

2차원적으로 보면 아래와 같은 형태가 되며

3차원 공간에서 가우시안에 대한 라플라시안은 거꾸로 뒤집은 모자 형태를 띔

이미지 미분

에지 검출을 하기 위해서

이미지 영상의 미분 수행이 필요하다.

이미지의 경우 y축 방향, x축 방향이 존재하는데 어떻게 미분하는가

연속 공간에서의 미분

우선 연속 함수의 도함수를 생각해보자

함수 f(x)에서 x에서 x의 미소증분이 0에 가까울때 변화하는 정도는 아래와 같이 구할수 있었다.

이미지에서의 미분

하지만 우리가 다루는 이미지는 위와 같은 연속이 아닌 이산적 공간에서 다루어야 한다.

그러므로 미소증분을 0이 아닌 1로 한 도함수를 정리하면 아래와 같다.

이는 영상 f(x)가 주어질때 [-1, 1] 마스크로 컨볼루션 하는것과 같은 결과가 나오게 된다.

이러한 영상은 이산 공간에서 미분을 취한것이므로 도함수, 미분 영상이라고 부른다.

이 영상을 특정 임계치로 이진화 시킨것을 에지 영상이며.

도함수 영상을 구할때 사용한 마스크를 에지 연산자, 에지 마스크라 한다.

이미지의 2차 미분

이미지의 에지는 밝기가 변하는 부분으로 조금더 자세히 살펴볼 필요가 있다.

대표적인 에지로는 계단 신호의 형태를 띄는 계단 에지와

램프 신호 형태의 서서히 변화하는 램프 에지가 있다.

아래의 에지 모델이 주어질때 1차 미분영상과 2차 미분 영상을 얻을 수 있다.

2차 미분에 대한 도함 수를 구하면. 다음과같이 [1, -2, 1]의 마스크를 구하게 된다.

1차 미분 영상을 살펴보면 계단이 시작하는 지점에서 봉우리 지역 극대점이 나오므로

1차 미분 영상 만으로 에지를 찾을수 있긴 하다.

하지만 실제 영상에서는 주로 서서히 변하는 램프 에지가 많으므로

아래와 같이 두께가 1인 이상적인 에지가 아니라

정확한 에지 검출이 어려운 경우가 많다.

그래서 이차 미분 영상을 통해 지역 극대점 뿐만이 아니라

영교차 zero crossing가 발생하는 지점이 명확한 에지라고 볼수 있다.

* 에지 검출 전 이미지 노이즈를 제거해주는것이 중요

2차원 이미지의 미분 영상(그라디언트)

지금까지 1차원 이미지 f에 대한 미분 영상을 다루었다

하지만 실제 이미지는 y와 x축을 가진 2차원 영상이므로

f(y, x)의 각 방향에 대한 미분을 고려하여야 한다.

각 방향에 대한 미분 영상들을 그라디언트 벡터. 그라디언트라 부른다

* 그라디언트 : 다변수 함수의 각 변수에 대한 1차 편미분

* 자코비안 : 다변수 벡터 함수의 각 변수에 대한 일차 미분

* 헤시안 : 다변수 함수의 이차 미분

ref : darkpgmr.tistory.com/132

그라디언트, 에지 강도, 그라디언트 방향

그라디언트는 벡터이므로 강도와 방향을 얻을수 있는데,

그라디언트 방향은 에지 방향과 수직이며,

그라디언트 강도는 에지일 정도를 의미한다.

이미지의 해상도 조절

- 업샘플링 : 해상도를 늘리는 영상 처리

- 다운 샘플링 : 해상도를 줄이는 영상 처리

- 이미지 피라미드 : 업샘플링/다운샘플링 연산을 통해 획득한 다중 해상도 영상

* 이미지 피라미드 예시

영상 처리의 기본 영상

- 점 연산 : 자기 값만 보고 새 값을 결정

- 영역 연산 aera operation : 이웃화소들을 보고 값을 결정

- 기하 연산 geometric operation : 기하학적 규칙에 따라 다른 값을 취하는 방법

점 연산

- 점연산의 대표적인 예시로 이진화

 -> 해당 픽셀이 임계치를 넘으면 1, 아니면 0

영역 연산

- 상관(필터)과 컨볼루션이 있음

상관 연산 filtering

- 1차원의 경우 : 윈도우(커널)을 입력 영상의 첫번째부터 끝까지 밀면서 연산

- 2차원의 경우 : 원도우(커널)을 0,0 좌표에서 일정 간격(스트라이드)밀면서 다음 행으로 넘어가도록 반복

컨볼루션 convolution

- 1차원의 경우: 상관 연산과 동일하나 윈도우(커널)을 뒤집어서 수행

- 2차원의 경우 : 상관 연산과 동일하나 윈도우(커널)을 뒤집어서 수행

상관 연산과 컨볼루션 구분 이유

- 물체 검출 용도의 경우 상관 연산 사용

- 신호 처리시 임펄스 응답을 얻기 위해 컨벌루션 연산 사용.

* 아래는 시불변 시스템에 임펄스 신호를 컨벌루션하여 임펄스 응답을 구하는 과정을 나타냄

커널(마스크, 윈도우)의 역활

- 정규 마스크 normalized mask : 마스크의 화소가 합하면 1이되는 마스크로 화소 평균을 구함.

- 가우시안 마스크 : 잡음 제거하며, 스무딩이라고도 부름

- 샤프닝 마스크 : 에지를 강조하는 역활 수행

- 에지 마스크 : 미분 연산자로, x방향, y방향 에지들을 강조하는 역활

* 아래는 가우시안 마스크와 가우시안 블러링 결과

* 에지 검출 용 마스크. 소벨 에지 마스크

비선형 연산

- 컨볼루션은 입력 이미지와 뒤집힌 커널의 선형 결합을 구하는 선형 연산

- 비선형 규칙을 적용하면 비선형 연산

메디안 필터

- 대표적인 비선형 연산 중 하나로 

기하 변환 geometry transformation

- 동차 좌표계에 동차 행렬을 곱하여

  이미지의 이동, 회전, 크기 기울기 변환 등을 수행하는 변환

- 강체 변환 rigid transform(유클리디안 변환) : 이동 + 회전

- 유사 변환 similarity transform : 크기 변환

- 어파인 변환 affine transform : 강체 변환 + 스케일링 + 기울기 

- 원근 변환 perspective transform : 어파인 변환 + 투영

ref : darkpgmr.tistory.com/79

이미지의 화소 pixel은 일반 적으로

사각형의 형태를 이용한다.

이진 영상의 예시

서로 만나는 화소의 관계로

4-연결성 4connectivity와 8-연결성 8-connectivity가 있음.

이번에는 확률 분포와 이들의 속성을 살펴볼건데

이 확률 분포들은 다양한 모델들을 만드는데 사용된다.

이번에는 베이지안 추론 같은 핵심 통계wjr 개념들을 살펴보고,

차후에 간단한 모델을 만들어보자.

N개의 유한개의 관측 집합으로 확률 변수 x에 대한 확률 분포를 구할건데

이 문제를 밀도 추정 density estimation이라 부른다.

이 문제를 다루기 위해서 모든 점 데이터들은 독립적이며 동일한 분포를 따른다고 가정할 것이며,

관측 된 데이터셋으로 너무 많은 확률 분포들을 구할수 있기 때문에 이런 밀도 추정의 근본적인 한계도 볼것이다.

그래서 이전에 다항 커브 피팅 시 적절한 분포를 선택하는 문제를 다뤄봤으며, 패턴 인식의 핵심 문제이기도 하다.

모수적 밀도추정 parametric density estimation

이산 확률 변수를 다루는 이항 분포와 다항 분포를 다뤄볼것이고, 연속 확률 변수에 대한 가우시안 분포를 살펴볼것이다.

이들은 평균과 분산같은 몇가지의 수로 주요 성질들을 나타낼수 있어

모수 분포 parametric distribution이라고도 부른다.

이 모델들로 밀도 추정에 사용하기 위해선, 주어진 데이터로부터 적절한 모수 값들을 찾아내어야 하는데

빈도주의자들은 가능도 함수 같은 몇가지 기준들을 최적화하는 방식으로 모수들을 찾아낸다.

베이지안의 경우에는 모수에 대한 사전 확률을 구하고,

베이즈 정리를 통해 관측 데이터가 주어지면 이로부터 사후확률을 계산한다.

여기서 켤레 사전 분포가 얼마나 중요한 역활을 하는지 보게 될건데 베이지안 분석을 간소화 시키게 한다.

* 켤레 분포 conjugate distribution : 베이즈 정리의 사전, 사후확률을 켤레 분포라 부름

* 켤레 사전 확률분포 conjugate prior : 결레 분포중 사전 확률 분포

* ref : en.wikipedia.org/wiki/Conjugate_prior

다항 분포의 모수에 대한 켤레 사전 확률 분포는 dirichlet 분포라 부르고,

가우시안 분포의 평균에 대한 켤레 사전 확률 분포는 다른 가우시안 분포가 된다.

이러한 모든 분포들을 확률 분포의 지수족이라 하며, 매우 중요한 속성들을 가지고 있으므로 자세히 살펴보아야한다.

비모수적 밀도추정 nonparametric density estimation

모수적 방법의 한계로는 특정한 확률 분포를 따른다는 점인데, 특정 상황에서는 부적절할 때가 있다.

그래서 이를 대신하는 방법으로 비모수적 밀도 추정 방법이 있는데,

이는 데이터 셋의 크기에 의존하는 확률 분포의 형태를 띄며

이 모델역시 모수를 가지고 있지만, 분포의 형태 보다는 모델의 복잡도를 제어한다.

마지막으로 세가지 비모수적 방법인 히스토그램과 최근접이웃, 커널 방법들을 살펴보겠다.