728x90
1. 정규 분포를 따르는 임의의 수 생성
clc;
clear all;
% 균일 분포를 따르는 임의의 수 생성
% randn(p, q)
% p : 생성할 데이터 행의 갯수, q: 생성할 데이터 열의 갯수
p = 5;
q = 5;
X = randn(p, q)
2. 평균과 공분산이 주어질때. 가우시안 임의의 수 Y를 생성하기(구형 과정의 경우)
- 아래의 식을 만족하게 만들면됨

- 샘플 데이터 집합 X = {x1, ..., xn}으로 구성, 샘플 데이터 갯수 N = 10000
- 평균과 공분산이 아래와 같이 주어질때 결과
* 공분산은 각 차원에서의 분산값이 모두 8000인 구형 확률 과정
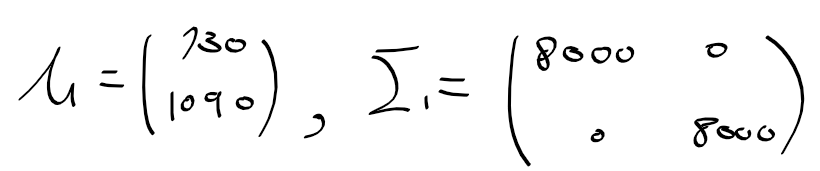
- Y(1:10, : ) => 1~ 10번째 샘플 데이터 출력
- scatter 함수로 1~ 500번째까지 샘플데이터 산점도로 출력
=> 평균 730, 1090을 중심으로 샘플 데이터가 구형 분포됨을 볼수 있음.
clc;
clear all;
N = 10000;
mu = [730, 1090]
sigma1 = [8000 0;0 8000];
X = randn(N, 2);
Y = X * sqrtm(sigma1) + repmat(mu, N, 1);
Y(1:10, :)
scatter(Y(1:500,1), Y(1:500,2));
grid on
axis tight
2. 대각 공분산인 경우
- 대각 공분산 성분만 존재하는 경우. 기울어짐 없이 데이터 축과 평행
clc;
clear all;
N = 10000;
mu = [730, 1090]
sigma1 = [8000 0;0 18500];
X = randn(N, 2);
Y = X * sqrtm(sigma1) + repmat(mu, N, 1);
Y(1:10, :)
scatter(Y(1:1000,1), Y(1:1000,2));
grid on
axis equal
3. 완전 공분산 행렬의 경우
- 축과 평행한 대각 공분산 행렬과 달리 한쪽 방향으로 기울어짐이 존재
=> 확률 변수간 상관관계가 존재. x1이 조금변할때 x2가 크게 변함
clc;
clear all;
N = 10000;
mu = [730, 1090]
sigma1 = [8000 8400;8400 18500];
X = randn(N, 2);
Y = X * sqrtm(sigma1) + repmat(mu, N, 1);
Y(1:10, :)
scatter(Y(1:1000,1), Y(1:1000,2));
grid on
axis equal
300x250
'수학 > 공업수학, 확률' 카테고리의 다른 글
| 통계 - 10. 오류 확률 (0) | 2020.08.04 |
|---|---|
| 통계 - 9. 우도비 검증 개요 (0) | 2020.08.03 |
| 통계 - 7. 다양한 가우시안 공분산 타입 (0) | 2020.08.03 |
| 통계 - 6. 가우시안 분포들 (0) | 2020.08.03 |
| 통계 - 5. 벡터 확률변수/다변수 확률변수 (0) | 2020.08.03 |