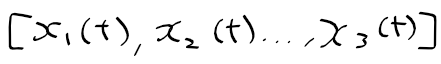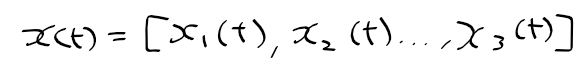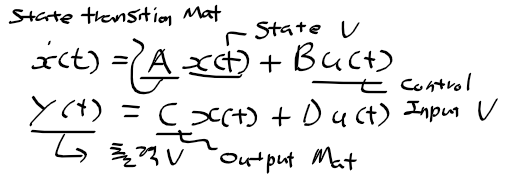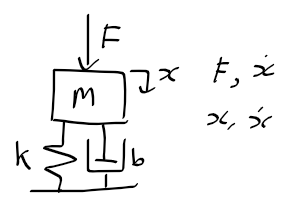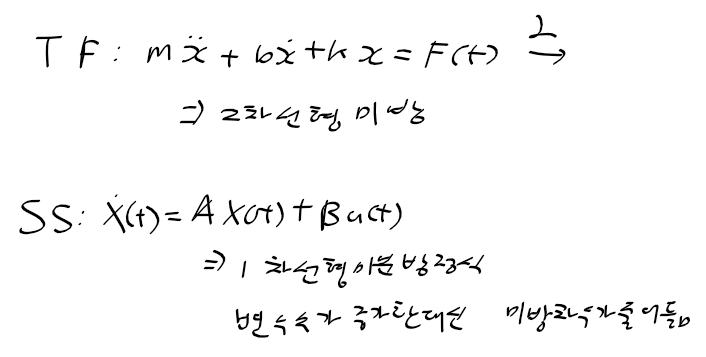제어공학 개요
제어공학 (Control Engineering)
- 제어 대상이 되는 시스템이 원하는 동작을 하도록 자동 제어 이론을 적용하는 공학
- 플랜트 Plant : 제어 공학에서 말하는 제어 대상
 폐루프 제어기
폐루프 제어기
제어의 예 | 빠르게 100m 달리기 vs 빠르게 100m에서 서기
1. 빠르게 100m 달리기
- 100m 라인을 빨리 지나기 위해 최대한 달리는 과정 -> 제어 과정 없음
2. 빠르게 100m에서 서기
- 100m 라인 직전/직후에 서기 위해 속도를 줄이거나 되돌아옴 -> 제어 과정으로 목표 달성
제어 공학의 역사
1. 고전 제어 ~ 1955
주파수 대역 제어기법
- 단일 입출력 선형 시불변 시스템에 적용
- 모델식은 전달함수
2. 현대 제어 1955 ~ 1975
시간 대역 제어기법
- 일반적인 시스템(비선형 시변 시스템)
- 모델식은 상태공간 모델
3. 탈현대 제어 1975 ~
시간 및 주파수 대역 제어기법(강인제어기법)/ 인공지능 제어기법
- 일반적인 시스템에 적용
- 모델식 : 상태공간 모델/ 전달함수 행렬, 인공지능(퍼지추론, 신경회로망) 모델
제어 시스템 발전 역사
- 1788 : Watt 증기기관용 원심 조속기
- 1868 : Maxwell의 증기기관용 원심 조속기의 수학적 모델 설정
- 1877 : Routh의 시스템 안정성 판별법 소개
- 1890 : Lyanpunov 비선형 시스템 안정성 판별법 소개
- 1910 : Sperry의 자이로스코프와 오토파일럿
- 1913 : Ford의 자동차 생산 위한 자동화 조립장치
- 1932 : Nyquist의 주파수 응답을 이용한 폐루프 시스템 안정도 판별법
- 1938 : Bode의 주파수 응답법 및 상태 안정도
- 1948 : Evans의 근궤적법
- 1952 : MIT에서 NC 수치제어 공작기계 개발
- 1956 : Pontryagin의 최적 제어 기법
- 1957 : 우주 시대를 연 인공위성 스푸트니크 발사
- 1960 : Kalman의 최적 추정 기법
- 1961 : Devel 산업 로봇
- 1969 :; Hoff의 마이크로 프로세서
- 1980 : Doyle, Stein, Zemes의 강인 제어 기법
- 1983 : PC 개발 및 제어설계용 SW 개발
- 1998 : 지능 마이크로 기계 및 나노 기계
- 2000 : 휴머노이드 로봇 ASIMO 개발
제어 공학 기본 용어
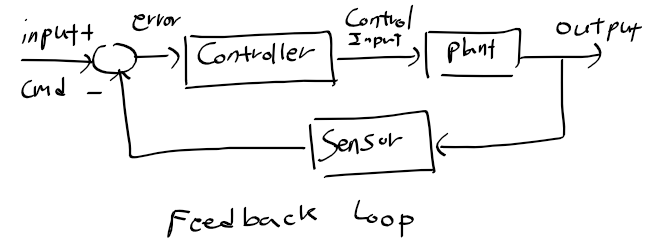
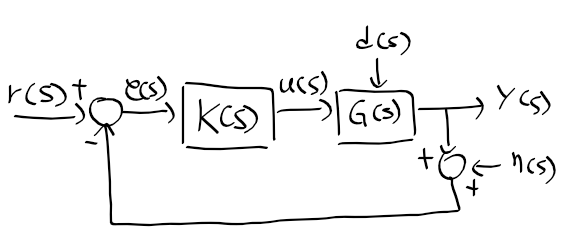 일반적인 피브댁 제어 시스템
일반적인 피브댁 제어 시스템
- G(s) : 제어 대상 시스템인 플랜트
- K(s) : 오차 신호에 따라 적절한 제어 입력을 생성하는 시스템인 제어기
- r(s) : 목표값 또는 요구값을 나타내는 기준입력, 명령입력, 목표입력
- d(s) : 외부로부터 제어 변수를 교란시키는 외란 입력
- n(s) : 센서를 통해 가해지는 센서 잡음 입력
- y(s) : 관심 있는 시스템 변수인 출력
- e(s) : 기준 입력과 측정된 출력 차이로 생기는 오차 신호
- u(s) : 플랜트 조작하기 위해 제어기에서 생성된 제어 입력
* s는 주파수 대역을 나타내는 문자
* 플랜트, 제어기, 센서를 어떻게 할것인가가 나머지 숙제
시스템
- 주어진 목표를 달성하기 위해 상호작용을하는 여러 요소들이 모인 하나의 복합체
1. 정적 시스템
- 시간에 따라 변하지 않는 시스템 timeinvariant ex) 가로등
- 출릭이 입력에 따라 결정
2. 동적 시스템
- 출력이 시간에 따라 변하는 시스템 timevariable ex) 달리는 자동차, 걷는 상태-위치
- 과거의 입력이 현재 출력에 영향을 미침
개루프 제어 시스템
- 플랜트 출력이 제어기에 아무런 영향을 주지 않는 제어 시스템

폐루프 제어시스템
- 플랜트 출력을 피드백 하여 기준 입력과 비교하여 그 차이가 없어질떄까지 제어하는 시스템

단일 입출력 시스템 SISO Single Input Single Output
- 입력 및 출력이 단일 변수인 제어 시스템
다변수 제어시스템 MIMO Multi Input Multi Output
- 입력/출력이 2개 이상 다변수인 제어 시스템
자동 난방 장치
- 피드백 : 실제 온도(출력)와 요구 온도(기준 입력)을 비교하여 그 오차를 제어 입력에 반영하는 과정
1. 제어 목적 : 방 20도 유지 -> 20도 기준 입력
2. 실제 온도가 20도가 안되면 오차에 의한 신호 발생 -> 보일러가 열공급
3. 20도 도달 -> 오차 0 -> 보일러 중단
4. 외부 열 누출 -> 방온도 하락, 오차 발생 -> 보일러 재가동
5. 이 과정이 반복되어 요구 온도 유지
 자동 난방장치 피드백 제어 시스템
자동 난방장치 피드백 제어 시스템
피드백의 장단점
- 장점
1. 시스템 불확실성에 대한 안정도, 성능 강인성
2. 시스템 성능 향상
3. 불안정 시스템을 안정한 시스템으로 바꿈
4. 비선형 시스템에 대해 넓은 작동 범위에서 선형성 증대
- 단점
1. 센서 장착에 의한 추가비용, 보수 유지비 등 경제적인 문제
(2) 제어 시스템 설계 절차
1) 수학적 모델링
1. 실제 물리적 시스템을 수학적 식으로 표현
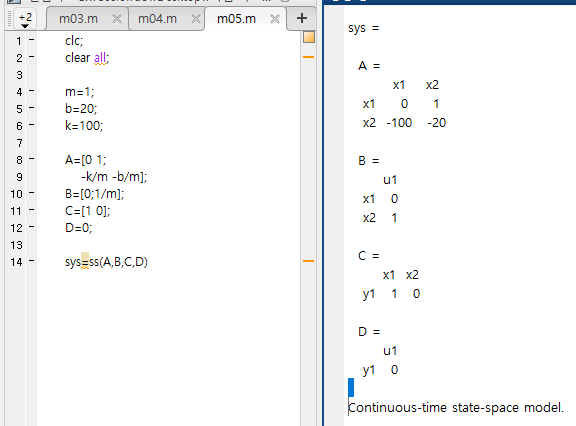
2. 전달 함수 또는 상태 공간 모델식으로 표현
3. 모델링 과정에서 모델링 오차에 의한 시스템 불안정성 고려해야함
- 실제 제어 시스템 성능 및 안정-강인성 문제
4. 수학적 모델링 방법
- 뉴턴의 제 2법칙을 이용한 동역학적 방법
- 블록 선도(Block Diagram)
2) 시스템 해석
- 시스템 안정도 및 성능을 예측하고 검토하는 과정
1. 안정도 평가
- 공칭 안정도 : 공칭 모델
- 안정성-강인성 : 모델링 오차를 고려한 실제 모델
2. 성능 평가
- 명령 추종 성능 : 출력 기준 입력
- 센서 잡음에 대한 저감도
- 외란 제거 성능
- 성능-강인성
3) 제어 시스템 설계 및 구현
- 비례-적분-미분(PID)
- 앞섬/뒤짐(Lead/Lag)
- 고유구조(Eigenstructure)
- LQ제어(Linear-quadratic control) 설계방법
- LQG제어(Linear-Quadratic Gaussian control) 설계방법
- 기술 함수를 이용한 제어기 설계 방법
- 입출력 선형화를 이용한 제어기 설계 방법
- 슬라이딩 모드 제어
- 적응 제어(Adaptive Control)
- 지능 제어(Fuzzy, Neural Network) 설계 방법
질량-스프링 시스템의 동적 특성 이해
스프링 시스템 특성
- 제어 : 시변 시스템
- 질량-스프링 : 기계적 시변 시스템의 기본 구조
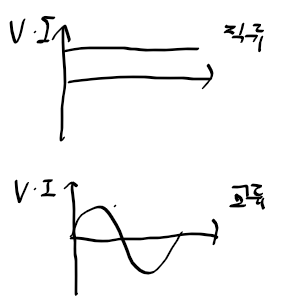
- 정역학 : 스프링에 가해지는 힘이 시불변인 경우
- 힘 F가 시간에 대해 일정하면 스프링 변위 x는 일정
- F와 x의 관계는 후크 법칙으로부터 F = kx로 시불변
* k는 스프링 상수이고 스프링 질량은 무시
 스프링 시스템
스프링 시스템
질량-스프링 시스템 동적 특성
- 시변(동역학) : 질량-스프링에 힘이 가해지는 경우
- 힘 F에 대해, 질량 m의 변위 x도 시간에 따라 변함
- F와 x의 관계 : 후크의 법칙과 뉴턴의 제2법칙 사용
 질량- 스프링 시스템의 F와 x의 관계
질량- 스프링 시스템의 F와 x의 관계
- 시변 시스템이므로 제어의 관심 대상
 질량-스프링 시스템
질량-스프링 시스템
힘 F가 시간의 함수로 주어질때 변위 x는 어떻게 구하는가?
- x의 일반해 = 동차해 + 특수해
- 동차해 complementary solution : 힘 F가 0일때 해
- 특수해 particular solution : F가 0이 아닌 특정 함수인 경우를 만족하는 해
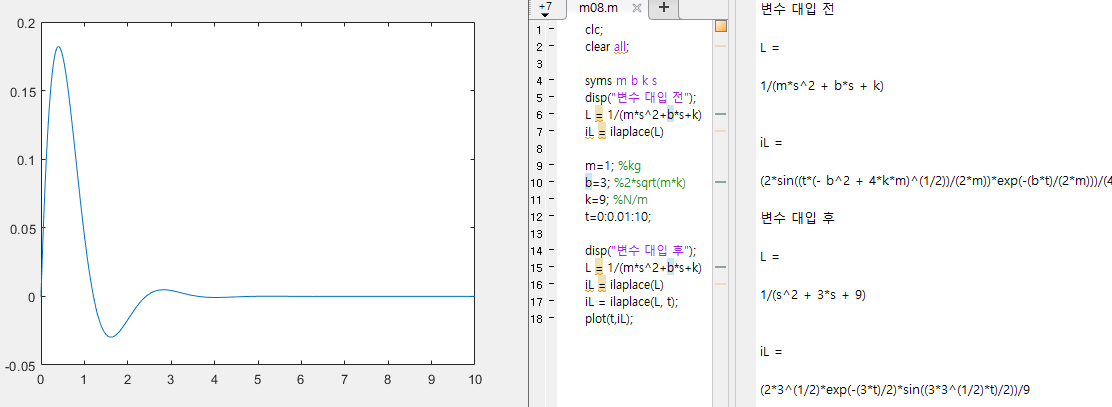
1. 동차 해. 라플라스 변환 적용
 동차해 계산
동차해 계산
2. 특수해
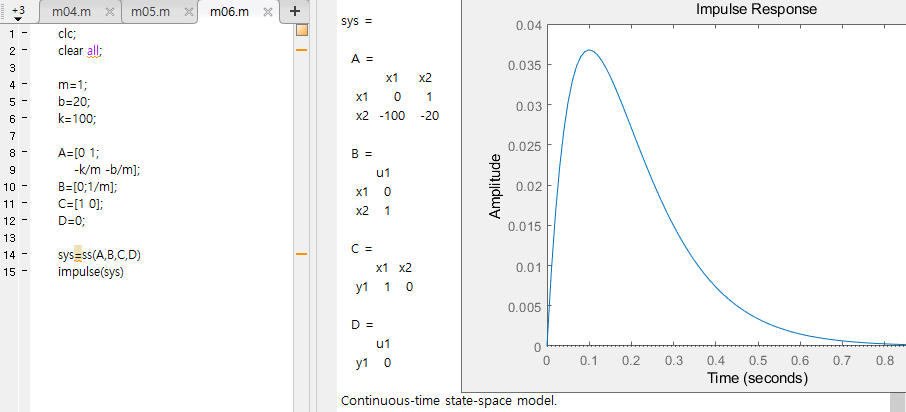
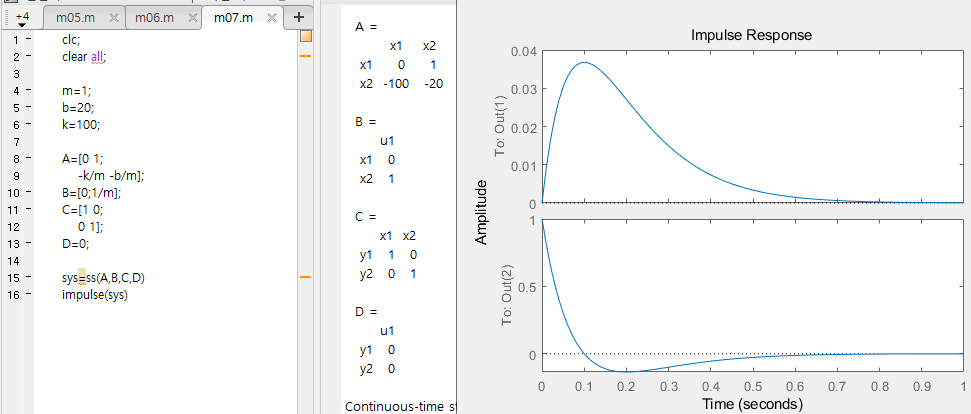
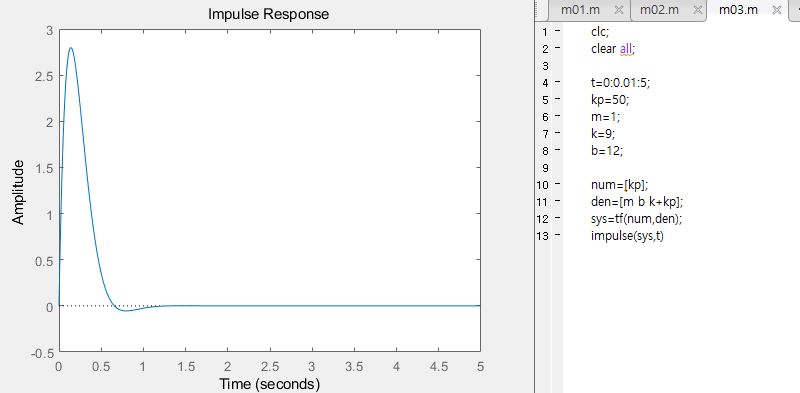
- 모든 초기 조건이 0이고, F는 임펄스 입력인 경우


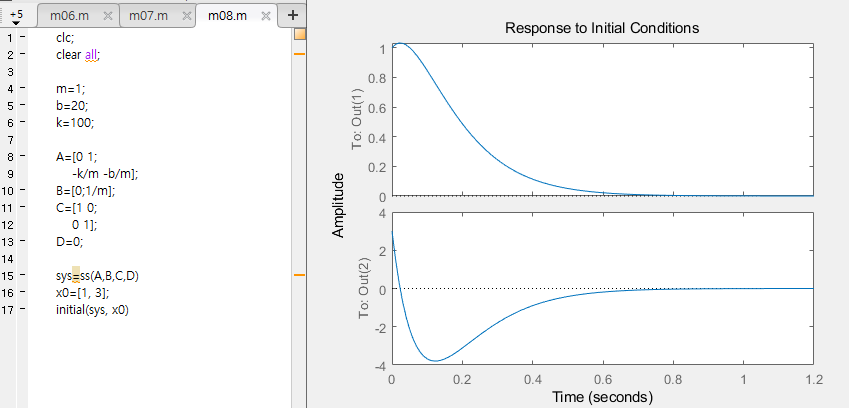
- 초기 조건이 0이 아니고, F는 임펄스 입력인 경우
-> 동차해와 특수해를 더하여 변위 x(t)를 구할 수 있음

 ,m = 1kg, k=9n/m, x(0) = 0.5
,m = 1kg, k=9n/m, x(0) = 0.5
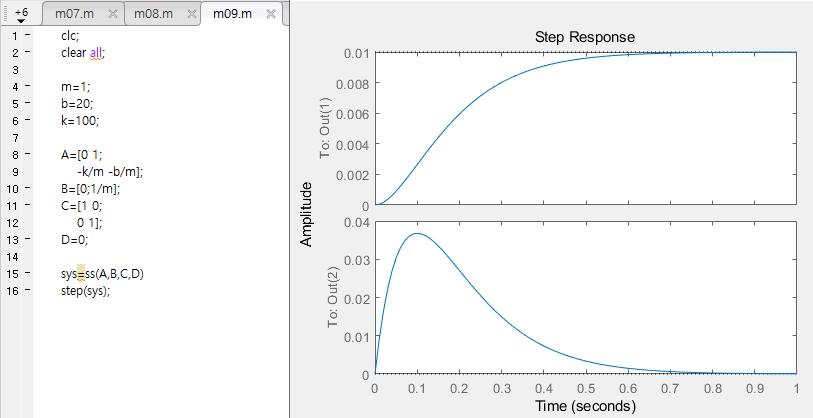
- 초기조건이 0이 아니고 F가 스탭 입력인 경우
- 질량-스프링 시스템에서 일정한 힘을 주어선 물체를 특정 변위로 가도록 제어 할 수 없다.