집밖은 위험해

2020-07-31

• 지난 시간에는 개선된 어셈블리어 코드를 이용한 부팅 가능한 이미지 파일 구현 방법과 병렬 처리 프로그래밍 openmp를 마무리 하고, 기술자에 대해서 조금 더 깊이 학습하여 주성분 분석과 얼굴 인식을 위한 고유 얼굴 검출 등 까지 과정들을 살펴보았습니다.
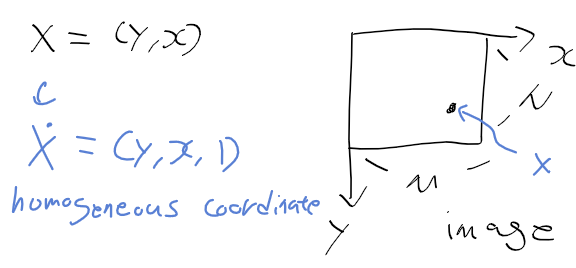
• 이번 시간에는 영상 위주로 학습을 진행하면서, 영상의 한 점에 대한 좌표와 특징 벡터로 이루어진 키포인트들 간에 매칭에 관한 전반들을 다루었습니다. 여기서 동일한 물체가 나오나 서로다른 영상에 존재하는 특징들을 매칭 시켜주기 위한 쌍을 찾고 어떠한 방식으로 최적의 쌍과 기하 정렬을 구하는지 살펴보았습니다.
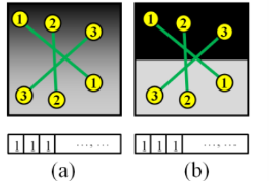
• 우선 가장 처음으로 매칭에 대해서 학습하였습니다. 매칭이란 서로 다른 영상 간에 존재하는 특징점 쌍이 서로 동일한 것인지 확인하는 과정이라 할수 있는데 이를 위해 유사도나 거리를 측정하여 매칭한 것인지 찾게 됩니다. 대표적인 특징으로 에지와 지역특징, 영역 등이 있으나 주로 매칭시에는 지역 특징이 사용되며 서로 다른 영상에 존재하는 특징들 간에 거리를 계산하기 위한 방법으로 유클리디안 거리와 마할라 노비스 거리가 있었습니다.
• 유클리디안 거리는 두 벡터 사이 요소 간의 차에 대한 노름으로 정리 할수 있었습니다. 하지만 유클리디안 거리는 데이터 분포에 대한 요소를 고려하지 못해 올바르지 않은 특징을 대응쌍으로 판단할수 있었습니다. 이를 개선한 마할라 노비스 거리는 유클리디안 거리 계산 중간에 데이터의 공분산 행렬을 추가하여 데이터 샘플 분포를 반영시킨 것으로 더 정확한 거리라고 할수 있었습니다. 추가적으로 매칭 성능을 판단하는 ROC 곡선에 대해서도 간단히 살펴보고 다음으로 kd 트리에 대해서 살펴보았습니다.
• 컴퓨터 비전에서 kd트리는 최근접 이웃인 특징을 빠르게 찾기위한 자료구조로 활용되었습니다. 한 영상에서 루트 노드로부터 분기해 나가면서 kd 트리를 만든다면, 다른 영상에서 구한 특징 즉 새로운 입력 특징이 주어질때 kd 트리를 이용하여 고속으로 최근접 이웃인 특징을 찾을수 있었습니다.
• 하지만 더 자세히 살펴보면 kd 트리를 이용해 최근접 이웃을 구하는 과정에서 지역 특징을 사용하다보면 기하 정렬 조건이 고려되지 않아 잘못된 형태의 매칭을 만들수 있습니다. 이러한 기하 정렬을 고려한 대표적인 알고리즘으로 최소 제곱법과 RANSAC 알고리즘을 사용하여 매칭을 수행하는 경우가 있었습니다. 최소 제곱법은 두 영상에서 구한 특징들 간에 오차를 최소한으로 하는 기하 변환 행렬을 구할수 있었으며, RANSAC에서는 거짓 긍정 오류가 존재하는 영상에 대해서 잘못된 특징쌍 즉, 노이즈를 제거하여 실제와 가까운 모델을 구할수 있었습니다.
• 이번 시간에는 매칭에 대한 거리 개념과 자료 구조, 최근접 이웃, 그리고 이를 기하 정렬을 고려하여 매칭을 하기 위한 알고리즘들 까지 전반에 대해서 살펴보았습니다. 사실 수식도 정리하고 더 깊이 살펴볼수 있는 내용들이기는 하나 깊이 있는 학습은 다음에 진행하고, 우선은 컴퓨터 비전 전체적인 범위를 살펴보는게 우선인 만큼 매칭에 관련된 개념과 알고리즘, 동작 과정이 어떻게 수행되구나 정도 까지만 학습하였습니다. 다음 시간에는 본격적으로 컴퓨터 비전에서의 인공지능, 기계학습 알고리즘과 활요에 대해서 학습해가고자 합니다.

kd트리 매칭

- 지역 정보만 사용

 => 첫 영상의 특징 벡터와 둘째 영상의 특징 벡터에서 최근접 이웃을 탐색하여 대응쌍 구함

기하 변환 Geometry Transform의 예시

- 같은 물체인 다른 대응쌍이 존재시. 기하 변환은 비슷해야함

- 예시 : Rigid Transform, Affine Transform, Perspective Transform 등

kd트리 매칭과 기하 변환

- kd트리 최근접 이웃 탐색을 이용한 매칭에서는 기하 정렬 조건 고려 x, 지역 정보만 사용

=> 기하 정렬 필요

기하 정렬 알고리즘의 사용 예시

- 잡음, 가림, 섞임에도 강건한 알고리즘으로 다음들이 존재

 -> 최소제곱법(거짓 긍정이 없는 상황), RANSAC(거짓 긍정이 존재하는 경우). 상황에 맞게 적절히 사용함

- 아래의 그림은 다양한 특징에다가 기하 정렬 알고리즘을 통해 매칭한 예시들을 보여줌

최소제곱법 least square method

- 주어진 샘플들을 가장 잘 표현하는 모델을 구함

- 아래의 예시는 점 집합이 주어질때 오차가 가장 적은 직선을 구하는 그림

컴퓨터 비전에서의 최소제곱법

- 일반 최소 제곱법에서 점 집합이 주어졌으나, 컴퓨터 비전에서는 특징 집합 X가 주어짐

- 대응 쌍이 같은 물체에 존재한다면, 같은 기하 변환을 가짐.

- 기하 변환 행렬(동차 변환 행렬) : 회전, 평행이동, 크기 변환 등을 포함

- 특징의 변환 : 아래의 동차 좌표가 주어질때, 동차 좌표와 동차 변환 행렬의 곱으로 기하 변환 결과 좌표를 구함. 

- 실제 측정한 점 b와 기하 변환을 통해 얻은 점 b' = x_dot H_dot이 주어질때,

  b와 b'의 최소 제곱 오차가 가장 줄여주는 기하 변환 행렬을 구해야 함.

최소제곱법을 이용한 매칭 예시

- 두 영상과 특징들이 주어질때, 매치 오차를 최소화 하는 기하 변환 행렬을 구한 예시

RANSAC을 이용한 매칭

- 두 영상의 특징 매칭 쌍 중에 거짓 긍정이 포함된 경우. 이를 노이즈로 보고 노이즈를 제거해야함

 => RANSAC 사용

순수 매칭 알고리즘

- 첫 영상 특징 벡터들에 대한 둘째 영상의 최근접 이웃 구함

=> 매칭쌍들을 mlist에 모음

- 아래의 그림은 이진 검색

kd트리

- 이진 검색트리의 예시

- 왼쪽 자식 노드는 기준 노드보다 작고 오른쪽 자식 노드는 기준 노드보다 큼

- 검색 키 : kd 트리에서 찾아야될 노드의 값

kd 트리 생성

- 특징

 1. 검색키는 스칼라가 아니라 벡터

 2. 검색 키에 가장 가까운 최근접 이웃 노드를 찾아야 함 

- n개의 특징벡터 X로 kd 트리를 만드는 경우, 하나의 특징 벡터 x는 d차원 벡터

- 루드 노드가 X를 두 부분 집합 X_left와 X_right로 분할

 -> 자식 노드에서도 계속 분할을 수행 => kd 노드 생성

kd 트리에서의 최근접 이웃 탐색

- 목표 : 특징 벡터 x입력이 주어질때 최근접 이웃을 찾기

- 입력 : x = (20,20)

- 과정 : 루트노드에서부터 분할해 나가며 입력에 가까운 노드를 찾아나감 -> 입력 벡터 x는 노드C에 최근접이웃

매칭 성능 판단

- 스테레오 비전과 파노라마서 여러장의 영상으로 매칭 수행

- 두 영상으로 매칭하는 경우. 첫 영상의 특징 벡터 a와 두 영상의 특징 벡터 b가 잘 매칭 => 매칭 쌍으로 판단

- 두 특징 벡터 a, b의 거리가 임계치 T보다 작으면 매칭쌍

임계치 설정하기

- T가 매우 작으면, 아주 가까운 쌍만 매칭

 => 진짜도 실패할 수 있음. 거짓 부정 FN 많이 발생

- T가 크면

 => 아닌 것도 성공함. 거짓 긍정 FP 발생

ROC Receiver Operating Charateristic 곡선

- 거짓 긍정률 FPR과 참 긍정률 TPR을 이어 만든 곡선

 => 매개변수에 따라 TP와 FP의 변화를 쉽게 보여줌

매칭 전략

- 서로 다른 영상에서 존재하는 특징이 매칭쌍인지 판단하는 방법

1. 고정 임계값 방식 : 거리가 고정된 임계값보다 작은지 확인 

2. 최근접 이웃 : 첫 영상의 특징 벡터 a가 주어질때 둘째 영상에서 최근접 벡터 b를 찾음.

3. 최근접 거리 비율 : 첫 영상 특징 벡터 a가 주어질때, 둘째 영상에서 최근접 특징벡터 b1과 다음으로 가까운 b2 취득

                      -> d(a, b1)/ d(a, b2) < T 이면 매칭

=> 최근접 거리 비율이 가장 좋은 성능을 보임

컴퓨터 비전에서의 매칭

- 서로 다른 영상간의 특징점 쌍이 동일한 것인지 확인하는 과정

- 유사성 or 거리를 측정하여 확인

 => 특징점 쌍 매칭에 거리 + 유사도 측정 척도가 필요

매칭에 사용하는 특징

- 에지

- 지역 특징

- 영역

SIFT 기술자의 거리재기

- SIFT 기술자는 128차원

- 두 점 a, b가 주어질때 이들의 거리를 측정해야함

- 방법 : 유클리디안 거리, 마할라 노비스 거리

유클리디안 거리

- 두 점 a, b가 주어질때, a와 b의 차로 구한 내적

- 유클리디안 거리가 작다 => 같은 지점을 나타낸다.

마할라노비스 거리

- 분산을 고려한 거리

- 아래의 경우 평균 mu와 점 b, 점 c가 주어질때 유클리드 거리상 점 b가 가까우나 이는 노이즈

- 점 c가 점 b보다 mu에 가깝다고 봐야함

=> 마할라노비스 거리 : 공분산을 고려한 거리

2020-07-30

• 지난 시간에는 대표적인 영상 특징 SIFT와 SURF의 특징과 영상 분할을 위한 다양한 방법, 특징 기술자 등 영상 관련하여 살펴보고, 병렬 처리 프로그래밍인 openmp에대한 개념과 간단한 실습, 그리고 간단한 윈도우 어플리케이션 해킹 실습을 진행하였습니다. 이번 시간에는 지난번에 기계어로 부팅 가능 이미지를 만들었던 것에서 개선하여 어셈블리어를 이용한 부팅이미지를 구현해보고, 어제 학습한 내용에 이어서 openmp의 기초적인 내용 학습을 마무리 하고자 합니다. 또 나머지로 특징 기술자 다음으로 영역 기술자와 주성분 분석, 그리고 이를 이용한 고유 얼굴 검출 및 얼굴 인식 과정에 대해 학습을 진행하고자 합니다.
• 어셈블리어를 이용한 부팅 이미지 구현 과정에서 일반 nasm 어셈블러 대신 nska라고 하는 어셈블러를 이용하여 이전에 기계어로 직접구현했던것 보다 간단하게 만들었습니다. 처음에는 Date Byte인 DB 명령어를 이용하여 16비트 값 하나하나 작성했던것 처럼 부팅 관련 이진값들을 입력해주었습니다. 중간에 공백 칸들은 공백으로 예약된 REVB Reserved Byte 명령어를 이용하여 공백이 필요한 부분들은 간단하게 공백을 삽입하여 기계어와 동일한 형태로 구현하였으며, QEMU 에뮬레이터에서 정상적으로 동작하는 모습을 확인하였습니다.
• 하지만 이러한 방식은 기계어로 코딩한 것과 별 차이가 없어 문자열을 사용하거나 다른 어셈블리 명령어를 활용하여 개선된 어셈블리 코드를 작성하였습니다. 여기서 추가로 사용한 명령어로 DW Data Word 데이터 워드를 저장하는 DW 명령어, 데이터 더블 워드 크기로 저장하는 DD등이 있었으며, 이전의 어셈블리 코드가 16진수만을 입력하였던것과 비교하면 문자열과 여러 명령어를 통해 훨씬 간결해진 코드를 구현할수 있었으며, QEMU와 Bochs 상에서 정상적으로 부팅이 되고 문자열이 출력되는 모습을 확인하였습니다.
• 또한 어제에 이어서 openmp 학습을 마무리 하였습니다. 오늘의 경우 병렬 프로그래밍에서 동기화를 다루는 방법과 중첩 스레드, 작업 분할 지시어, 스케줄링과 테스크 등의 개념들에 대해서 전반적으로 살펴보고 실습을 진행하였습니다. openmp는 스레드 기반 병렬프로그래밍으로 하나의 프로세스 내부에서 동작하다보니 스레드 안에 스레드를 생성하는 경우 중첩 스레드로 처리하는 방법에 대해 이해가 필요하였습니다. 그래서 중첩 스레드가 어떻게 생성이 되고 데이터들의 범위가 정해지는지, 그리고 병렬 처리할 작업들을 스레드마다 균일하게 배분할것인지 동적으로 배분할것인지에 대한 작업 분할 지시어, 그리고 작업 단위인 테스크를 어떻게 효율적으로 처리할지에 대한 스케줄링 기법과 여러개의 스레드가 같은 데이터를 동시에 다루는걸 막기위한 동기화 로직 등 지난 시간에는 간단한 연산과 사용법, 예제들을 살펴보았다면 오늘은 조금더 고급적인 활용 방법들을 살펴볼수 있는 시간을 가졌습니다.
• openmp 수업을 마무리하고나서 영상 처리 일부분을 마저 진행하였습니다. 우선 지난 시간 SIFT 특징 기술자에 대해 살펴보면서 특징 기술자가 무엇인지 그리고 어떤 구성요소를 가지고 있는지, 계산하는 과정을 다루었다면 이번시간에는 개선된 특징 기술자와 영역을 다루는 기술자, 주성분 분석 방법과 이를 이용한 얼굴 인식에 대해 학습을 할 수 있었습니다.
• 우선 개선된 특징 기술자로 PCA-SIFT와 GLOH를 살펴보았습니다. SIFT의 경우 4 x 4 x 8 = 128바이트 크기를 차지하는 만큼 일반 영상에는 특징들이 많이 존재하므로 컴퓨터의 성능이 크게 저하될수 있습니다. 그래서 이런 벡터의 정보를 손실을 줄이면서 차원수를 줄이는 기술인 PCA를 적용한 SIFT 즉, PCA-SIFT에 대해서 살펴보고, 이와 별개로 SIFT 기술자가 사각 마스크에서 적용되었다면, 원형 마스크를 사용한 GLOH 기술자에 대해서 간단히 학습하였습니다.
• 다음으로 영역 기술자에 대해서 살펴보았습니다. 특징 기술자가 하나의 특징점, 키포인트에 대한 추가적인 정보였다면 영역 기술자는 공간에 대한 정보를 나타낸다고 할수 있습니다. 영역 기술자는 전역 기술자와 지역 기술자가 존재한다고 할수 있는데, 전역 기술자인 경우 대표적으로 에지가 많이 활용된다고 합니다. 하지만 전역 기술자로서는 영상의 일부분 변화를 처리할수 없기 때문에 지역 기술자를 위주로 학습하였습니다.
• 지역 기술자에서는 아까 특징 기술자에서 상당히 계산량이 많았던 관계로 지역 이진 패턴 방법들이 주로 사용된다고 합니다. 대표적인 LBP Local Binary Pattern은 특징점 주위에 마스크를 씌워 이에 픽셀들의 대응쌍을 찾는데 이 픽셀 쌍은 이진값을 가지는게 특징이 됩니다. 이를 통해서 해당 영역에 대한 텍스처 정보를 보존할수 있어, 얼굴 인식 문제에 적용하는 경우 얼굴을 여러가지 셀로 분할하고 각 셀에 대한 LBP 히스토그램을 만듦으로서 얼굴 인식을 위한 모델을 만든다고도 합니다.
• 마지막으로 주성분 분석과 고유 얼굴, 즉 얼굴 인식에 대해서 살펴보면서 마무리 하였습니다. 주성분 분석은 큰 차원의 벡터를 최대한 정보 손실을 줄이면서 저차원의 벡터로 만드는 기술이라 할수 있습니다. 여기서 고유 얼굴은 입력 얼굴과 평균 얼굴의 차이 영상이라 할수 있습니다. 이 고유 얼굴에 주성분 분석을 적용하여 저차원의 고유 벡터를 구하게 되고 이 고유벡터와의 가장 거리가 가까운 고유 얼굴을 찾음으로서 누구의 얼굴인지 판단하는 기술임을 정리하였습니다.

얼굴 인식

- 컴퓨터 비전 분야에서 주성분 분석을 가장 잘 사용하는 경우로 얼굴 인식이 있음.

평균 얼굴

- 여러개의 얼굴에 대한 평균 영상

고유 얼굴

- 얼굴 영상에 PCA를 적용하여 얻은 고유 벡터

1) 평균 얼굴 획득

2) 입력 얼굴 영상 - 평균 얼굴

3) 공분산 행렬 취득

=> 고유 벡터와 고유값 계산

고유 얼굴 이용한 얼굴 인식

1. 원래 얼굴 벡터 x로 고유 얼굴 벡터 y 획득

2. 입력 얼굴 xi가 주어지면 고유 얼굴 yi로 변환

3. 입력 고유 얼굴 yi와 고유 얼굴 벡터 y의 원소 들 중 거리가 가장 가까운것을 검색

* 거리가 임계값이상이면 다른사람, 없는사람

주성분 분석 PCA Principal Component Analysis

- 고차원의 벡터를 정보의 손실을 줄여 저차원의 벡터로 변환하는 기술

 => 차원 축소, 변수 추출 방법으로 널리 사용됨

- 아래의 예시에서 2차원 데이터를 1차원 데이터로 변환한 예시들을 보여줌

 => 원래 데이터의 분산을 가장 잘 보존하는 축을 찾아야 함

텍스처

- 특징 추출, 영역 분할에서 많이 사용

- 영상의 질감 -> 반복되는 일정 패턴

텍스처 분석과 구조적 방법

- 구조적 방법 structural method

-> 기본 요소텍셀을 추출후 텍셀의 공간적 배열 탐색

- ex. 꽃밭 영상의 경우 -> 꽃이 텍셀

- 텍스처를 추출 할 대상은 지역적일수도 전역적일수도 있음 -> 어렵게 만듬

전역 기술자

1. 영상의 에지를 텍스처 기술자로 사용

2. 명암 히스토그램을  사용

=> 문제: 지역적 변화는 반영 불가

지역 관계 기술자

- 픽셀 간 관계 정의 및 표현 방법 필요

-> 동시 발생 행렬, 지역 이진 패턴

동시 발생 행렬 coocurrence matrix

- 명암 픽셀 쌍들을 조사하여 이웃간의 관계 정의 필요.

- 동시 발생행렬에서 행은 픽셀 쌍의 명암값, 열은 발생 횟수 표현

-> 명암 영상은 길이가 256이므로 256 x 256 크기로 동시 발생 행렬이 만들어짐.

지역이진패턴

- 지역적인 영역의 이진 패턴으로 텍스처 기술

- 종류

LBP Local Binary Pattern

LTP Local Ternary Pattern

LBP 지역 이진 패턴

- 텍스처 분류를 위한 특징이나 얼굴 인식 등에서도 많이 활용

- 모든 픽셀에 대해 계산. 중심 픽셀 주위의 밝기 변화를 이진화한 패턴

LBP와 얼굴인식 예시

- 얼굴 영역을 일정 크기 셀로 분할

- 각 셀별 LBP 히스토그램(LBP 인덱스 값에 대한) 계산

- 히스토그램들을 직렬로 연결한 벡터를 최종 특징으로 사용

 => 일종의 탬플릿 매칭

 * 셀 단위로 기하학적 정보 유지, 셀 내에선 텍스처 정보만 추출

LBP의 단점

- 명암이 균일한 부근에서 불안정

-> 명암들이 비슷한 부분에서는 어떻게 0과 1로 이진화 시킬까?

LTP Local Ternary Pattern

- 매개변수 t를 설정

- 중간 픽셀 화소에서 +- t 범위 안이면 0. +t보다 크면 1, -t보다 작으면 -1

- LTP 생성 : 2개의 LBP 생성됨 -> 512차원

=> 0, -1 -> 0, 1 -> 1으로 히스토그램 생성. LBP 1개

=> 1, 0 -> 0, -1 -> 1으로 히스토그램 생성. LBP 1개

PCA-SIFT

- 주요 방향 dorminant direction을 구하는 과정은 SIFT와 동일

- 특징 벡터 x 추출 과정이 다름

1) 키포인트 중심으로 39 x 39 윈도우 씌움

2) 윈도우 안 픽셀에 대해 y방향 x방향 도함수 영상 계산

3) 39 x 39 = 3,042 차원 벡터 획득 -> 너무크다

4) PCA Principal Component Analysis 주성분 분석으로 차원 축소하여 특징벡터 x로 취급

=> 4 * 4 * 8 = 128차원인 SIFT 기술자보다 PCA-SIFT는 차원 수를 크게 줄일수 있음

GLOH

- Gradient Location Orientation Histogram

- 원형 마스크(필터, 윈도우) 사용

- 원은 3등분, 두 바깥원들은 각각 8등분

- 분할된 영역들(16 + 1= 17개)에서 16단계 그라디언트 방향 히스토그램 계산

=> 17 x 16 = 272 차원 특징 벡터

- PCA 수행하여 272 -> 128차원 특징벡터로 취급 

이진 기술자

- 이전에 살펴본 특징 기술자들은 개당 128차원의 특징 벡터로 영상 처리하기엔 너무 큼

- 특징점 주위 두 픽셀을 비교쌍으로 사용. 픽셀들을 조사 후 수백개의 쌍으로 이진 배열 생성

- ex: BRIEF, ORB, BRISK

- 이진 기술자 조서 패턴 : 특징점 주위의 비교쌍들의 한쪽은 1, 한쪽은 0의 값을 가짐

이진 기술자들의 특징

- BRIEF : 가우시안을 따르는 두 점 조사 -> 스케일/회전에 영향 받음. 256개의 비교쌍 -> 256비트

- ORB : 회전 불변, 512 비트

- BRISK : 60개 점 설정 및 거리 조건 만족하는 쌍만을 비교쌍으로 사용. 회전 + 스케일 불변, 512 비트

이진 기술자와 일반 기술자 비교

- BRISK : 512비트

- SIFT 기술자 : 특징점 주위를 4등분. 한 영역에 4 x 4 x 8 = 128바이트. 128 x 4 = 512바이트

- BRISK의 크기 = SIFT 기술자의 크기/8