컴퓨터 비전 - 27. SVM

분류기 일반화 성능

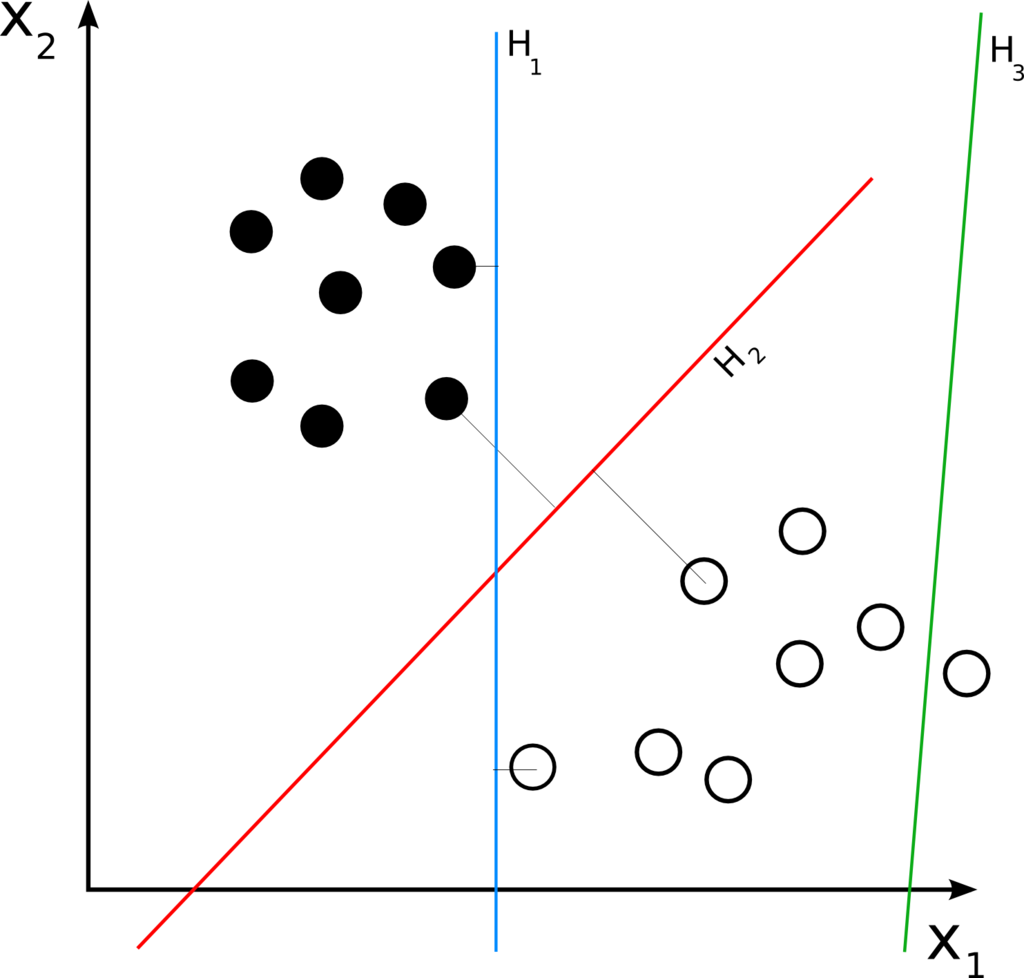
- 다음의 샘플이 주어질 떄, 다양한 분류 모델이 제공될 수 있음.

- 학습 과정을 통해 분류기는 학습 데이터들을 가장 분류하는 H2로 수렴함 => 일반화 성능이 가장 좋음 

https://ko.wikipedia.org/wiki/%EC%84%9C%ED%8F%AC%ED%8A%B8_%EB%B2%A1%ED%84%B0_%EB%A8%B8%EC%8B%A0

 

SVM

- 기존의 분류기들은 오류 최소화(최소 제곱법 least square method)하는 방향

- 서포트 벡터 머신은 오류 최소화 + 마진 최대화 하여 일반화 능력을 극대화 시킨 알고리즘

- 선형 회귀 모델을 다루는 선형 SVM과 비선형 모델을 다루는 비선형 SVM이 존재

 

 

선형 SVM

- 이진 분류 binary classification 수행하는 결정 초평면 decision hyperplane에 대한 식은 아래와 같이 정리할 수 있음.

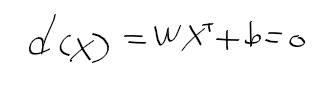
- 결청 초평면을 이용한 선형 분리

 

 

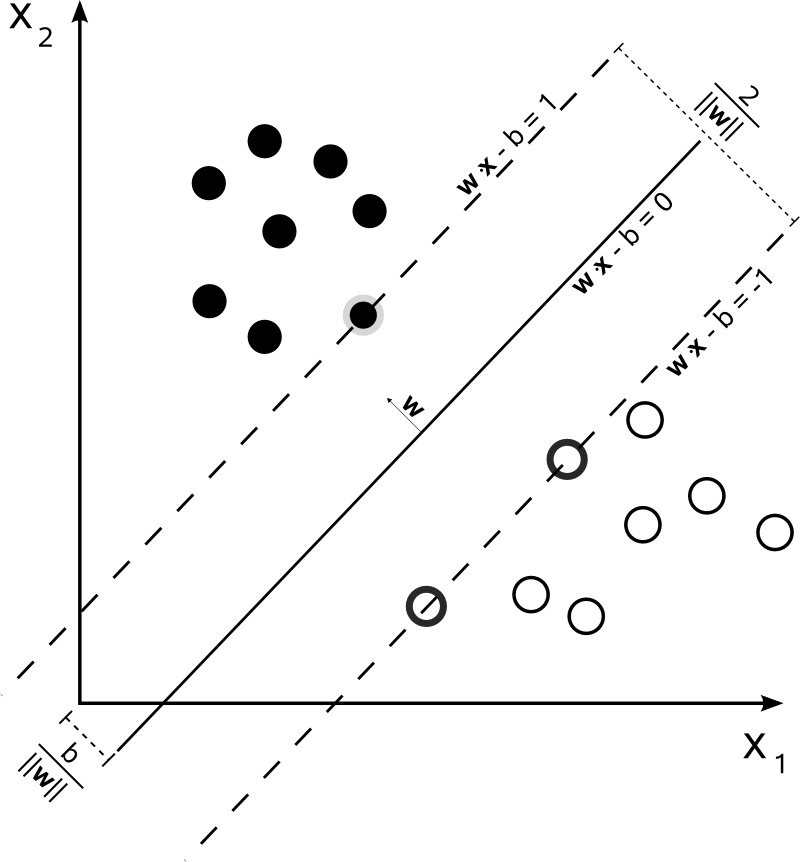
선형 SVM과 결정 초평면 hyperplane

- 여백 margin을 최대화 화는 결정 초평면의 기울기 w를 구해야 함

 => 최적화 문제로 다루게 됨

- 서포트 벡터 support vector : 여백의 크기를 결정하는 샘플들

 => 서포트 벡터까지의 거리가 최대로 되도록 조절하는 결정 초평면 찾기

 

 

SVM과 최적화 문제

- 결정 경계 decision boundary와 서포트 벡터까지의 거리가 1이 되도록 한다면 다음과 같이 정리 가능

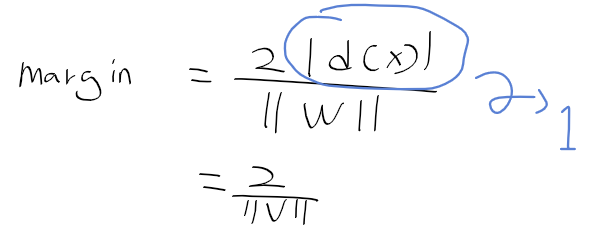
-아래와 같이 학습 집합을 정의

- 모든 샘플들을 올바르게 분류하는 결정 초평면 hyperplane 찾기

 => 조건부 최적화 문제 constrained optimization problem이 됨

- 아래의 조건이 주어질때 등호가 성립하는 경우가 서포트 벡터

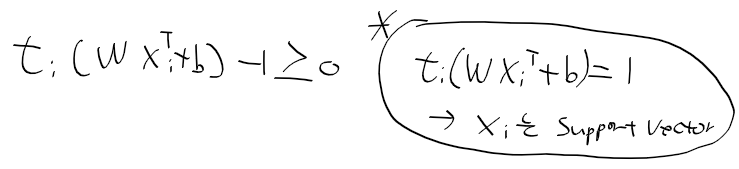
- 최적화 문제를 다음과 같이 정리

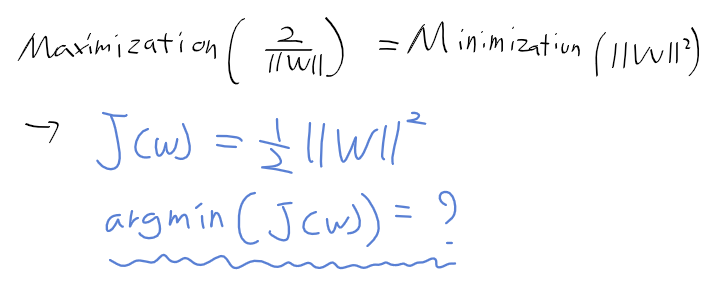
라그랑주 승수와 조건부 최저화

- 위 조건식에 라그랑주 승수 alpha_i를 부여

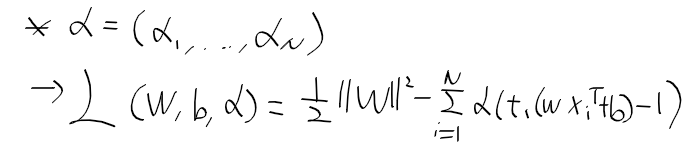
- 함수 L을 w와 b로 미분후 0으로 정리. 

 

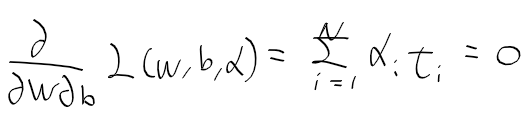
- KKT Karush-Kuhn-Tuckker 조건식을 유도하여 정리하면, 아래의 식을 최대화 하는 라그랑주 승수를 구하는 문제가 됨.

 

 

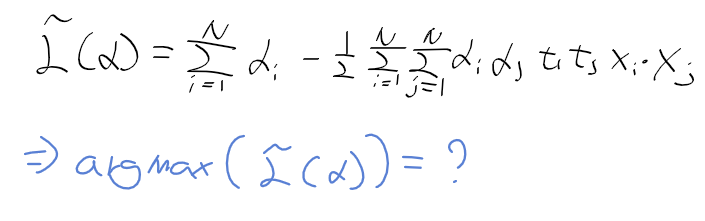
선형 SVM과 비선형 SVM

- 결정 초평면으로 선형 분리가 불가능 한 경우도 존재

https://stackoverflow.com/questions/44606126/linear-svm-vs-nonlinear-svm-high-dimensional-data

 

 

비선형 SVM

- 2차원 공간(input space)에서 선형 분리가 불가능 한경우, 3차원의 공간(feature space)에선 결정 평면 decision surface로 선형 분리가 가능

- 아래의 그림과 같이 매핑 함수 Phi를 사용하여 3차원 공간으로 확장 가능

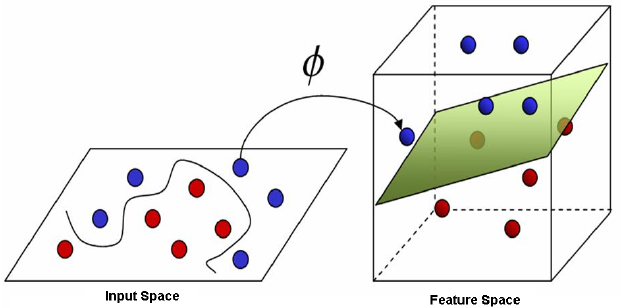
- 매핑 함수를 이용해 조건부 최적화를 다루는 목적  함수로 정리 가능

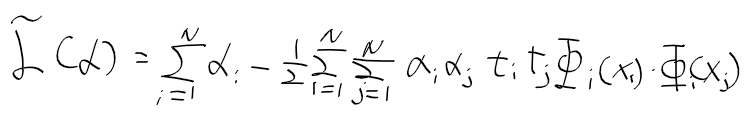
- 매핑 함수는 고차원이라 실제로는 사용 불가 -> 매핑 함수의 내적인 커널 함수로 사용 가능