집밖은 위험해

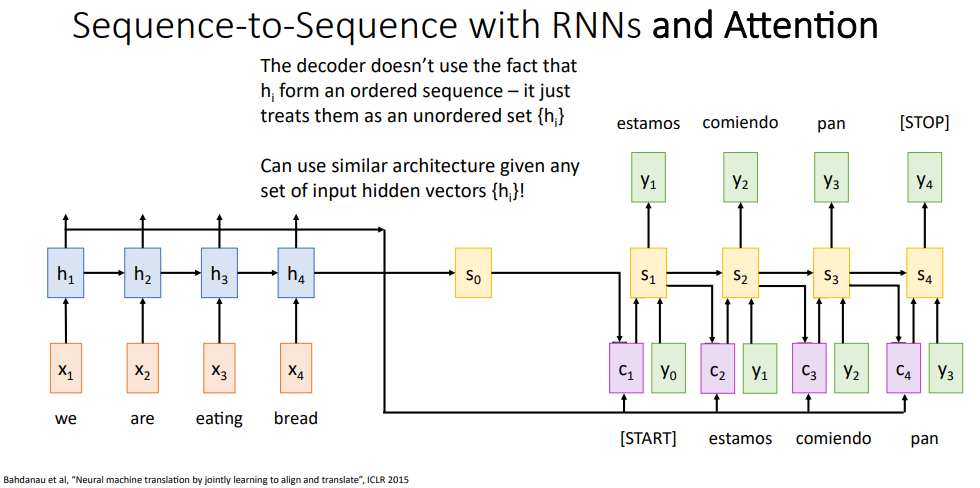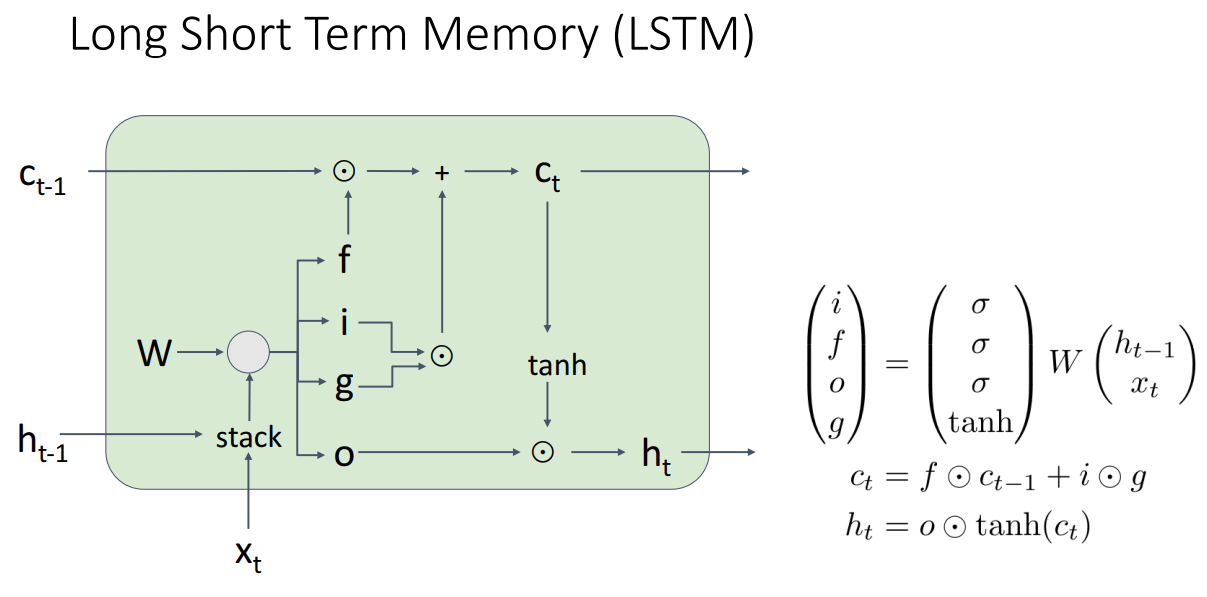
 신경망이 무엇을 찾고 있는지 이해하기위해서 우리가 사용해볼수 있는 또 다른 방법으로는 신경망의 가중치가 아닌 신경망의 중간 활성값을 시각화해보는 방법입니다. 이전에 합성곱 신경망을 공부했던걸 떠올려보면, 신경망의 각 계층에서는 활성값을 계산하며 마무리합니다.

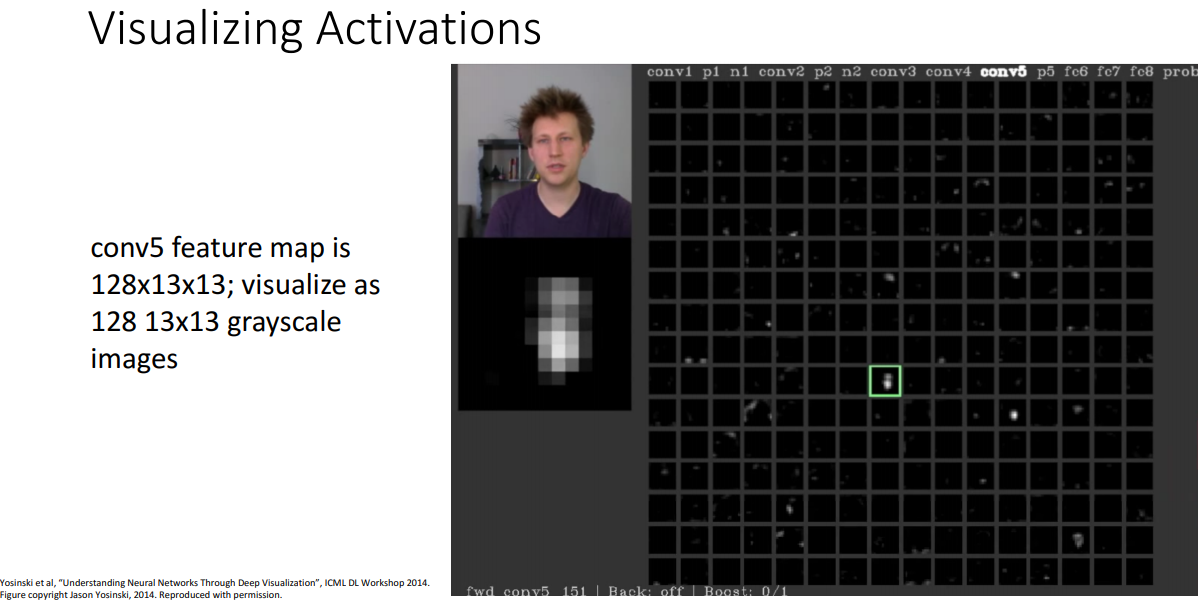
 한번 알렉스넷의 5번째 합성곱 계층 예를 들면, 여기서 13 x 13 크기의 128채널의 값을 계산하는데, 이는 알렉스넷의 5번째 합성곱 계층에서 128개의 필터가 있고, 각 필터들은 13 x 13 그리드 형태의 값들을 가지게 됩니다. 여기서 우리가 해볼수 있는건 13 x 13 크기의 활성값들을 흑백 이미지로 시각화해볼수 있어요. 

 여기서의 개념은 필터의 값이 0에 가깝고, 렐루 함수를 통과시키면, 대부분의 값들이 0이 될겁니다. 하지만 특징 맵이 0이 아니라면, 입력 이미지가 들어오면 서로 다른 합성곱 필터들이 입력 이미지의 어떤 특징에 반응을하는지 이해할수 있습니다.

  여기서 진행한 시각화결과를 보면 128개의 합성곱 필터의 활성 결과들을 볼수 있는데, 필려의 출력 중 하나로 녹색 부분을 골라 봅시다. 왼편에 원본 이미지와 아래에 시각화결과가 있어요. 그러면 13 x 13 그리드의 영역들에서 이 필터가 입력 이미지의 사람 얼굴 부분을 따라 활성된것을 볼 수 있습니다. 이는 신경망 한 레이어의 한 필터가 정확하다고 하기는 힘들지만 사람의 얼굴 혹은 사람의 피부톤에 반응한게 되겠습니다.

 서로 다른 이미지에 대해서 여러 레이어의 활성 결과들을 이용해서 서로 다른 필터가 무엇에 반응하는지 이해할수 있겠습니다.

(질문) 필터들의 활성 결과가 왜 대부분이 검은색일까요?

 저의 생각에는 렐루 비선형 함수 때문입니다. 랠루 함수를 다시 떠올려보면 음수 값이 들어오는경우 0이 나오게 되고, 양수만 남게 됩니다. 그렇다보니 많은 값들이 0이 되고, 0이 아닌 부분들은 꽤 중요하다고 볼수 있겠습니다. 또 이건 시각화의 산물이라고도 할수 있는데, 신경망이 0 ~ 무한대의 실수 값을 출력하는데, 시각화할때 0에서 255로 줄여내기 때문입니다. 그래서 출력을 어떻게 줄여나갈지에 따라서 이미지의 전반적인 밝기에 영향을 줄 수 있어요.

 임의의 이미지나 임의의 필터를 보는게 아닌 다른 해볼수 있는 방법으로는 최대 활성 패치 Maximally Activating Patches로 이건 신경망에서 최대로 활성화하는 패치를 말합니다. 

이전 슬라이드에서 우리는 신경망 한 계층의 이 필터가 얼굴에 반응하는걸 배웠습니다. 그래서 우리가 전체 테스트셋에 대해서 가설 검정을 하고싶을때 우리가 해볼수 있는건, 

  전체 훈련셋을 가지고 와서, 전체 훈련셋과 테스트셋을 신경망에다가 돌리는데, 레이어와 필터를 골라 그 레이어에서의 필터의 값을 저장합니다. 우리는 이미 합성곱 신경망에서 특징 그리드의 각 원소들은 입력 이미지의 유한한 크기의 패치와 대응되는걸 알고 있어요. 3  x 3 합성곱 계층의 경우 입력 이미지의 3 x 3 크기의 덩어리로 계산하고, 여기다가 3 x 3 합성곱 층을 쌓으면, 입력 이미지의 5 x 5 크기의 부분의 영향을 받아요.

 그래서 우리가 해볼건 레이어와 필터를 선택하고, 전체 훈련/테스트셋을 돌려보고, 테스트셋 이미지의 패치중에서 우리가 선택한 필터에 가장 크게 반응하는 패치들을 찾아냅니다. 그리고 이것들을 기록하면됩니다.

 오른쪽에 시각화한 결과물들이 있는데, 위의 그리드는 신경망의 한 레이어에 들어온 입력들을 보 여기서 각 행은 그 레이어에 있는 한 필터에 대응하는 것들이며, 한 행의 각 컬럼 요소들은 이미 학습된 신경망의 선택된 레이어와 필터에 아주 아주 크게 반응하는 훈련 이미지의 패치입니다. 

 그래서 이들은 신경망에서 선택된 뉴런을 최대로 활성화하는 테스트 셋 이미지들의 패치들이기도해요. 최대 활성 패치를 시각화함으로서 뉴런들이 무엇을 찾는짖 이해할수 있습니다. 예를들면 맨 위에있는 행을보면 강아지의 코처럼 생긴것들이 있는데,  그러면 이건 강아지의 코를 찾는 뉴런이라고 할수 있겠습니다.

 위 그리드의 4~6번째 행은 모두 영어 단어나 텍스트 패치로, 이 텍스트들은 전면과 후면이 다른 색상과 다른 방향을 가지고 있어요. 즉, 심층 신경망에서 선택된 이 필터는 서로다른 색상과 방향을 가진 텍스트를 찾는걸 알수 있겠습니다.

 아래의 그리드에서도 같으나 더 깊은 레이어에서 동작하는 실험을 해보았습니다. 신경망의 더 깊은 계층에서 실험을 하다보니 각 뉴런의 값은 입력 이미지의 더 큰 패치로 구한다(입력으로 부터 멀수록 수용장은 커지므로). 그래서 심층 레이어에서의 최대 활성 패치는 더 커지게 되겠다.

 아래 그리드에서 두번째 행을보면 모든 최대 활성 패치들은 사람 얼굴인데, 이 얼굴들이 다른 피부색상, 다른 위치에 있다. 하지만 깊은 곳에있는 한 뉴런 혹은 한 필터가 학습한 결과 어떻게든 사람 얼굴을 인식하게 되었습니다.

 최대 활성 패치 기법으로 신경망의 중간 계층에서 어떻게 인식되는지 이해하기위한 또 다른 방법을 얻을수가 있는데, 신경망이 무엇을 계산하는지 이해히기 위해 해볼수 있는 다른 방법으로 입력 이미지의 어떤 픽셀들이 분류 문제에 중요한것인가를 찾는방법이 있습니다.

 여기서 우리가 해보려는건 왼쪽에 코끼리의 이미지가 있고, 이 코끼리 이미지가 학습된 신경망에서 올바르게 코끼리로 분류되었다고 가정합시다.  이제 우리가 알고자하는건 입력 이미지의 어떤 픽셀들이 신경망이 코끼리로 분류하는걸로 결정을 내리는데 중요한가가 되겠습니다.

 그래서 우리가 해볼수 있는 방법은 코끼리 이미지를 준비해서 이미지의 일부 픽셀을 회색 사각형이나 혹은 균일한 색상으로 바꾸고, 이 마스크 처리 된 이미지를 신경망에다가 돌려보면 됩니다. 그렇게 하면 신경망이 마스크화된 이미지를 무엇으로 분류하기를 원하는지에 대해 갱신된 스코어를 얻을수가 있습니다.  이 사각 마스크를 다른 위치로 이동시키면서 이 과정을 반복할수 있고, 서로 다른 마스크 이미지들을 신경망에 돌리겠습니다.

 모든 위치의 경우로 마스크를 이동시키면서 이 과정을 반복하면 각 지점에서 코끼리의 확률을 계산해내고, 이걸 saliency map으로 만들어낼수 있습니다. 이건 어떤 픽셀이 분류에서 중요한지를 알려줘요. 오른쪽에 이 이미지가 있는데, 입력 이미지의 모든 지점에다가 마스크를 넣어보고 마스크된 이미지를 신경망에 돌린 결과를 코끼리일 확률에 대한 히트맵으로 만들었습니다.

 여기서 알수 있는점은 코끼리부분에다가 마스크를 한경우 코끼리로 예측할 확률이 떨어지는걸 볼수 있으며, 이는 신경망이 분류 결정을 할때 이미지의 올바른 부분을 보았다고 할수 있겠습니다.

 이러한 실험을 다른 두 이미지로 반복해보았습니다. 위의 스쿠너(범선)이미지인데 배가 있는 부분에 마스크를하면 신경망이 스쿠너 클래스로 분류할 확률이 아주 떨어지는걸 볼 수 있고, 하늘에다가 마스크를 한 경우에는 크게 중요하지 않다보니 신경망이 크게 신경쓰지 않으며 여전히 스쿠너로 올바르게 분류할수 있습니다.

  이러한 방식은 우리가 신경망이 어떻게 동작하는지 이해하고자 할때, 어떤것들이 중간 특징들을 활성시키는지 보는것대신 입력 이미지를 단순히 변형시키고, 입력이미지의 어떤 부분이 신경망이 올바르게 분류하는데 사용하는지 볼수 있었습니다.

 여기서 놀라운 점은 신경망은 이미지의 어떤 부분이 물체인지 혹은 배경인지 알 필요가 없는것이며, 신경망이 단지 모든 스쿠너들이 특정 색상의 물위에 항상 있다면 배를 자체를 보지 않고 물의 색상만을 보고 스쿠너로 분류할수도 있습니다.

 만약 우리가 가진 데이터셋이 신경망이 치팅할수 있는것이라면, 신경망이 이미지의 엉뚱한 부분을보고 올바른 정답을 말할수 있는 데이터셋이라면 신경망은 쉽게 치팅하도록 학습을 할 것이고, 이러한 경우 시각화 할 시 신경망이 치팅을 하는지 그렇지 않고 이미지의 올바른 부분을 보고 결정을 하는지를 알수 있겠습니다. 

(질의응답) 이건 나쁜 방법.

 saliency map을 마스킹으로 구하는것은 가능한 모든 위치에다가 마스크를 놓고 계산을돌려야하다보니 계산 비용이 아주 큰 문제가 있음.

 다른 방법으로 역전파를 이용해서 saliency map을 구할수 있습니다. 입력으로 귀여운 강아지 임지를 준비하고, 신경망으로 돌려 강아지일 확률을 계산하겠습니다.

 그리고 역전파를 하는동안 강아지일 스코어와 입력 픽셀들 사이의 그라디언트를 계산할 수 있는데, 이는 입력 이미지의 모든 픽셀들이 약간 변할때 신경망의 맨끝에서 강아지 분류 스코어에 얼마나 영향을 미치는지 알려준다. 이건 적대적 예시로서 생성하는데 사용할수 있는 이미지의 그라디언트로, 이 예시의 경우 유령같은 그라디언트 이미지를 시각화해서 볼수 있으며, 각 픽셀은 강아지 스코어에 대한 각 픽셀들의 그라디언트가 되겠다. 

  이 그림을 보면 강아지의 윤곽선 같은게 보이고, 분류 스코어에 영향을주는 픽셀들은 주로 강아지 안에 있는걸 알수 있겠다. 강아지 밖에 있는 픽셀이 변하더라도 분류 스코어는 크게 변하지는 않겠다. 이런 방법을 통해서 신경망이 이미지의 올바른 부분을 보고있는걸 알수 있다.

 강아지 이미지 말고도 다른 이미지에다가도 적용하여 다른 이미지에서 어떤 픽셀들을 신경망이 중요하게보는지에 대한 saliency map을 얻을수도 있습니다. 이 예시들에서 짚고 넘어가고 싶은 부분은 이 논문에서 소개된 이 기술은 대부분의 실제 예시에서는 좋은 결과가 나오지 못하고 있습니다. 그래서 과제를 하면서 생각보다 좋지 못한 결과가 나와서 놀랄수도 있어요.

 이건 버그가 있는게 아니라 논문 저자가 예시를 신중하게 골른것이고, 하지만 여전히 신경망이 무엇을 학습하는지 이해하는데 꽤 좋은 방법이라 생각합니다.

 saliency map을 잘 동작하도록 하기위한 방법으로 이미지에 있는 물체를 어떠한 지도없이 분리시키는것인데요. 여기에 메뚜기 이미지가 있는데 이걸 신경망에다가 넣고, 신경망은 이미지가 메뚜기로 분류할거에요.

 이제 우리가 할일은 입력이미지로부터 메뚜기 이미지 부분 픽셀들을 구하는것인데, 우리가 해볼수 있는 일은 saliency map를 사용해보면 됩니다.  신경망으로 계산하여 saliency map을 구하고, 영상 처리 기술(위 슬라이드에서는 grabcut 사용)을 적용합니다. 그러고 나서 다시 이미지 분류로 학습된 신경망을 객체 카테고리에 해당하는 입력 이미지의 색션으로 분할하는 용도로 사용합니다.

 제가 아까 이야기했지만 여기서 고른 예시들은 잘 동작하지만 이 기술은 일반적인 경우에는 잘 동작하지 않을수 있습니다. 하지만 각 픽셀에 대한 그라디언트 정보를 계산하는 이 방법, 이미지에서 픽셀의 변화가 얼마나 최종 스코어에 영향을 주는지 계산하는 것은 신경망이 어떻게 동작하는지 이해하는데 매우 유용하다고 할수 있겠습니다.

  이번에 살펴볼 방법은 이미지의 픽셀이 최종 클래스 스코어 어떤 영향을 미치는가가 아니라 신경망 안에 있는 중간 특징들이 무엇을 찾고 있는지에 대한 질문으로 되돌아가서 봅시다. 이 질문에 대한 대답으로 우리는 그라디언트 정보를 사용할수가 있어요.

 여기에 우리가 해볼수 있는것으로 신경망의 어느 레이어를 선정하고, 어떤 필터를 골라봅시다. 여기서 할일은  훈련 이미지나 테스트 이미지를 신경망에다가 넣어서 돌리면서 역전파를 하겠습니다. 그런 다음에 입력 이미지의 어느 픽셀이 최종 클래스 스코어에 영향을 주었느냐가 아니라 어느 중간 뉴런 값이 영향을 주었느냐를 보겠습니다.

 제가 입력 이미지의 픽셀들을 바꾼다면 중간에 있는 뉴런들의 값이 올라갈거나 내려가게 되겠죠. 

(질문) saliency map은 훈련전의것인가요? 훈련 후의 것인가요?

 saliency map을 훈련 전에 구해보면 아주 좋지않은 결과가 나옵니다. 합성곱 구조는 계산 과정에 있어서 강한 규제 효과를 가지다보니 학습 전이라해도 saliency map을 구하면, 여러분들이 훈련 전에 시각화하더라도 좋은 결과를 얻기는 힘들고 아마 랜덤한 결과가 나오겠습니다.

  그래서 이렇게 그라디언트 정보를 사용해서 중간에 있는 특징이 무엇을 찾는지 이해하는 것과 같은 아이디어를 사용해서, 코끼리 입력 이미지를 신경망에 넣어 중간 레이어까지 돌림으로서 최종 스코어까지 역전파하는게 아니라 이 중간 뉴런의 값에 대한 역전파가 어떤 입력 이미지의 픽셀이 이 중간 출력 뉴런에 가장 영향을 주는지 알려줍니다.

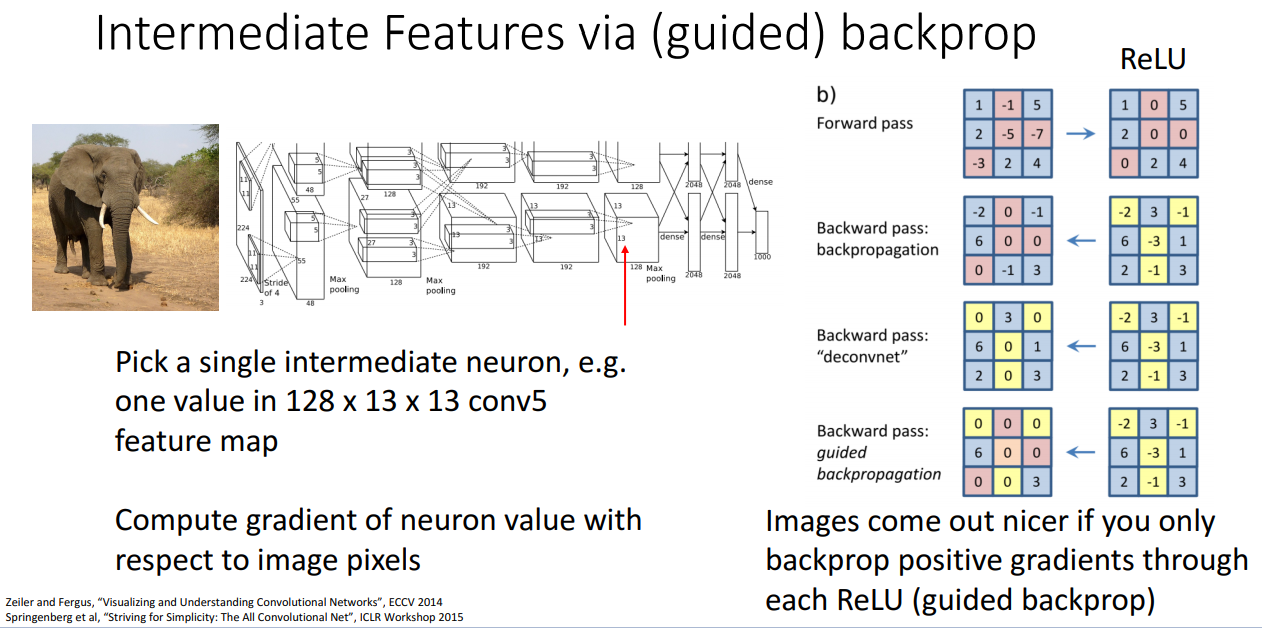
   일반적인 역전파 방법으로 구한 중간 특징에 대한 결과가 좋지 않게 나오다보니, 연구자들이 guided back propagation이란 방법을 사용하였습니다. 이게 왜 동작하는지 완전히 이해할수는 없지만 좋은 결과가 나옵니다.

 이 guided back propagation이라는 개념은 우리가 알다시피 순전파를 할때 0이하의 값은 모두 0으로 설정되고, relu를 역전파로 통과 시 순전파 때 0이 되었던 위치들이 마스크처럼 적용되서 업스트림 그라디언트로부터 온 값들이 0이 됩니다. 업스트림 그라디언트에 (0마스크를) 적용한게 relu함수의 일반적인 역전파가 되겠습니다.

 이번에는 guided backpropagation에서는 relu 함수를 역전파로 통과시에 거기다가 음수의 업스트림 그라디언트에다가도 마스크처리를 합니다. 다시말하면 relu 함수를 역전파할때 해당하는 모든 업스트림 그라디언트의 값은 0이 되고, 거기다가 음수인 업스트림 그라디언트도 0이 되요. 즉, 추가적인 마스킹으로 모든 음의 업스트림 그라디언트도 제거하는게 되겠습니다. 저도 이런 방식으로 이미지를 시각화하는데 역전파를 사용할때 더 좋은 결과가 나오는지 모르겠습니다.

 아무튼 이런 guided back propagation을 이미지에 적용하면, 뉴런 값에 변화를 주는 이미지의 픽셀들을 잡아낼수 있다. 왼쪽 그림이 최대 활성 패치들이면, 우측에 있는 것들이 guided back propagation을 적용해서 이 패치의 어떤 픽셀들이 뉴런에 영향을 주는지 찾아낸 결과이다. 맨 윗 행의 결과들을 보면 이 뉴런들이 강아지의 코나 눈을 찾고 있는걸 알수 있고, guided backpropagation의 결과를 보면 이러한 것들이 뉴런 값에 큰 영향을 주는걸 확인할 수 있다. 

 더 깊은 신경망 레이어의 최대 활성 패치들을 구해서 또 적용시켜보면 비슷한 결과를 얻을수가 있다. 이전에 사람 얼굴을 찾았던 뉴런을 봤었는데, 사람 얼굴의 픽셀을 위주로 보는것을 확인할수 있다. 이 방법은 테스트셋의 이미지나 패치에 한정해서 본 것이고 더 나아가서 

 guided back propagation으로 테스트셋 이미지에다가 이미지의 어떤 픽셀이 뉴런 값에 영향을 주는지 찾아내었는데, 테스트 이미지셋만 보지말고 모든 가능한 이미지들 중에서 어떤게 이미지가 최대로 뉴런 값을 찾아내는지 볼수 있습니다. 그래서 뉴런의 값을 최대화 시키는 syntetic image를 생성해보겠습니다.

 이걸 이미지 픽셀들에 대해서 경사 상승으로 만들어 낼 수가 있는데, 위 슬라이드의  I*가 특정 뉴런을 최대화 시키도록 생성한 이미지이고, f(I)는 이미지가 주어질때 특정 뉴런의 값, R(I)는 생성한 이미지가 자연스럽게 하기 위한 규제자가 됩니다. 이 식은 신경망 가중치를 학습할때 본것과 비슷한데, 여기서 하고자 하는건 가중치를 갱신하는게 아니라 중간에 있는 특징 중 하나를 최대로 활성 시키는 이미지를 구하는게 되겠습니다. 이 이미지는 경사 상승 알고리즘을 통해서 구할수 있는데 이미지를 그라디언트 정보로 조금씩 바꿔가면 되요.

 이걸 하기 위해서 우선 0이미지나 랜덤 노이즈로 초기화하고, 이 이미지를 신경망에다가 돌린뒤 선택한 뉴런의 값을 구합니다. 그리고 역전파를 통해서 이미지의 어떤 픽셀들이 뉴런값을 변화시키는지 찾아내요. 이미지를 약간 갱신시키고, 이 과정을 반복함으러서 선택한 뉴런이 큰값을 갖도록 영향을 주는 인공 이미지가 만들어집니다.

 이번 14번째 강의에서는 합성곱 신경망 내부에서 시각화 하는 기술에 대해서 살펴보고, 이것들을 이해하여봅시다. 이번 강의 제목은 약간 의미가 잘못된 부분이 있는데, 오늘 다루고자 하는 두 주제는 하나는 신경망 안을 드려다 보는 기술로 데이터가 어떻게 학습되는지를 이해하는 것이고, 두 번째로는 신경망을 시각화하고 이해하는 다양한 기술들인 deep dream과 style transfer에 대해서 살펴보겠다.

 지난 강의에서는 어텐션에 대해서 다뤄보면셔, 어떻게 어텐션 메커니즘이 순환 신경망 모델에다가 추가시켜 매 타임스탭마다 입력의 다른 부분에 집중을 시키는지와 어텐션이라는 개념을 신경망 모델에서 레이어로 사용할수 있도록 일반화 시켜보았다. 그리고 새로운 레이어로 셀프 어텐션 레이어를 만들고, 이걸 트랜스포머라고 부르는 새 신경망 모델을 만드는데 사용하였다. 이 모델은 입력을 처리하는데 어텐션만 사용한다.

 우리는 그 동안 다양한 종류의 데이터들을 처리하는 신경망 모델을 만드는 방법에 대해서 배워왔습니다. 그래서 이미지를 처리하는 합성곱 신경망 모델을 어떻게 만드는지 알고있고, 순환 신경망 모델로 시퀀스를 처리할수 있는데다가 트랜스포머로 시퀀스나 데이터셋을 처리할수 있겠습니다.

 수업끝나고 많은 학생들이 물어보거나 이번 강의 내내, 시각 인식 작업에서 신경망 모델이 무엇을 학습했다고 우리가 어떻게 말할수 있는지에 대한 질문이 자주 있습니다. 이런 커다란 합성곱 신경망이 있고, 이 모델을 큰 데이터셋으로 학습시키면, 신경망 내부에 있는 특징들을 무엇을 찾고 있을까요?

 우리가 신경망 내부를 들여다보고, 서로다른 특징들이 서로다른 레이어들이 보고 있는 것을 얻어낸다면, 신경망 모델이 어떻게 실패하게 되는지 아니면 어떻게 동작하는지 아니면 어떡게 동작이 안되는지에 대해서 이해할수 있을거에요. 그래서 우린 사람들이 이런 깊은 신경망의 안을 들여다보기위해서 사용하는 방법들에 대해서 다뤄보고, 모델 내부에서 어떻게 돌아가는지 이해해봅시다.

 우선 말하자면 이들은 경험적으로 찾아낸 방법같은 것이지 내부에서 어떻게 돌아가는지 알아내는 아주 좋은 이론적인 방법은 아직 없습니다. 하지만 경험을 통해서 얻은 여러가지 방법들로 레이어가 어떻게 반응하는지에 대해 더 알수 있겠습니다.

 그런 방법들 중 하나는 신경망의 첫번째 레이어를 시각화하는 것입니다. 선형 분류기를 다시 떠올려보면, 선형 분류기는 각 클래스당 한 탬플릿으로 탬플릿들의 집합을 학습하는 개념이었는데, 선형 분류기로 각 클래스당 스코어 계산을 템플릿과 입력 이미지의 내적으로 간편하게 구하였습니다.

 이를 일반화 시키고, 신경망 그러니까 합성곱 신경망에다가 적용시켰습니다. (선형 분류기를 합성곱 신경망에다가 적용시킨) 이 개념이 순방향 연산과정에서 하는 템플릿 매칭입니다. 그래서 합성곱 신경망의 가장 첫번째 레이어에서는 여러 필터들을 학습시키는데, 이 필터들은 입력 이미지를 쭉 슬라이팅 시켜서 학습합니다. 필터는 입력 이미지의 모든 지점과 학습된 필터의 각 지점을 같이 내적 연산을 합니다.

 이 탬플릿 매칭 개념으로 학습하고 나면, 합성곱 신경망의 첫번째 레이어의 필터들을 rgb 이미지처럼 시각화함으로서 시각화를 할수있겠습니다. 이미지와 필터를 내적한다는 개념으로 필터를 이미지 처럼 시각화 할때, 그 필터를 시각화한 이미지는 그 필터랑 가장 강한 반응을 하겠습니다. 그래서 이런 필터들을 시각화해서, 신경망의 첫번째 레이어가 어떤 것을 찾는지 어느정도 이해할수 있겠습니다.

 지금 보는 슬라이드에서는 이미지분류를 위한 이미지넷 데이터셋으로 네 합성곱 신경망 모델을 선 학습 한 것에서 첫번째 합성곱 필터를 시각화 한 결과를 볼수 있겠습니다. 여기서 알아차릴수 있는 부분은 이런 신경망 아키텍처들이, 알렉스넷, resnet, densenet로 아키텍처는 꽤 다르지만, 첫번째 레이어에서 학습한 필터들은 아주 비슷하게 생긴걸 볼수 있습니다.

 또, 이런 필터들을 보면, 다른 방향의 에지를 찾는 에지 방향 필터도 있고, 반대되는 색상을 가지는 필터도 많이 있는걸 볼수 있습니다. 한번 이전에 봤던 humble and weasel의 포유류 시각 시스템 실험을 떠올려보면, 포유류의 시각 시스템은 시각장에서 우리가 보고 있는것에 대한 방향 에지를 찾는 셀을 가지고 있는데, 이는 합성곱 신경망 첫번째 레이어가 학습한 필터들과 비슷하다고 볼수 있고, 그래서 합성곱 신경망의 첫번째 레이어는 여러 종류의 방향 에지나 여러 종류의 색상들을 찾아내는거라고 이해할수 있겠습니다. 

 이 기법을 합성곱 신경망의 높은 레이어에다가 적용해도 되겠습니다. 하지만 정보가 그렇게 많진 않아요. 이 슬라이드를 보면 cfar 분류 데이터셋을 학습한 3층 합성곱 신경망의 가중치를 그냥 시각화 한걸 볼수 있는데, 첫번째 레이어를 시각화하면 이전 슬라이드에서 봤던게 나오지만 나머지 두 레이어를 시각화를 한 결과 이미지 여러 덩어리들이 나오게 됩니다.

 이는 이 작은 신경망 모델의 첫번째 레이어가 7 x 7 크기의 필터 16개를 가진다고하면, 두번째 레이어는 16개의 채널을 입력으로받아 20개의 필터로 만들다보니 출력한 20개의 합성곱 필터들은 16개의 입력 필터로 부터 구하지만, 16채널의 이미지는 채널수 때문에 RGB 이미지로 시각화하는데 좋지는 않아요.

 그래서 대신 출력된 각 20개의 필터 각각의 16개 필터들은 7 x 7 크기의 흑백 이미지로 시각화 시킬수 있습니다. 슬라이드에서 처럼 보기에는 불편할수 있지만 조금 더 고차원 합성곱 필터에서 공간적 구조를 조금 더 볼수 있겠습니다. 여기서 블롭 패턴이나 에지같은걸 찾을수도 있지만 RGB공간 상에서는 더이상 에지나 블롭을 찾을수는 없고, 이건 이전 합성곱 레이어로부터 생성된 특징 공간 상에서 블롭과 에지를 찾는 과정이라 할수 있겠습니다.

 이런 시각화 방법을 이용해서 고차 합성곱 필터가 어떻게 돌아가고 있는지 볼수는 있겠으나 이 필터들이 무엇을 찾는중인지 명확하게 이해하기는 어렵겠습니다. 그래서 합성곱 신경망의 다른 레이어에서 어떻게 되어가고 있는지 이해하려면 다른 방법들을 사용해야 해요.

 신경망을 이해하기위한 다른 방법중 하나는 중간 합성곱 레이어들을 무시하고, 마지막 완전 연결 계층에서 어떤 일이 일어나는지 살펴보는 방법이 있습니다. 알렉스넷을 떠올려보면, FC7 layer는 4096개의 특징들을 가지고 있어 이걸로 마지막 선형 변환을 해서 이미지넷 데이터셋에대한 1000개의 클래스들의 스코어를 구할수가 있습니다.

 여기서 우리가 해볼수 있는 일은 4096차원의 벡터로 표현되는걸서  이해하려고 하면되는데, 우리는 이미 학습된 알렉스넷이 어떤일을 하는지 알아내기 위한 방법은 입력 이미지를 4096차원의 벡터로 바꾸고, 선형 분류기를 적용하면 되는걸 알고있으니 이 과정에서 시각화를 통해 4096벡터에서 어떤 일이 일어나는지 이해할수 있겠습니다.

 그래서 정리하자면 훈련된 알렉스넷 모델 같은걸 준비해서, 이미지 테스트셋을 돌려 각 이미지에 대한 특징 벡터들을 계산하고 모은 다음에 다양한 기법들로 시각화 해볼수 있어요.

 우리가 해볼수 있는 간단한 방법으로 4096차원의 벡터에다가 최근접이웃을 적용해보는게 있습니다. 이전에 했던 두번째 과제에서 로 픽셀 데이터에 최근접 이웃 탐색을 사용했었는데, 왼쪽 그림이 픽셀 값을 이용한 최근점 탐색을한 예시에요. 그러면 실제 비슷한 클래스나 의미를 가진 무언가를 찾기 보다는 비슷한 픽셀들을 가진 이미지를 찾아냅니다.

  이번에는 이미지의 로 픽셀에다가 최근접 이웃을 적용하는게 아니라 알렉스넷으로 구한 4096차원의 벡터로 최근점 이웃 탐색을 하는것인데, 이 특징 공간에서 가장 가까운 이미지가 무엇인지 찾아낼수가 있어요. 중간에 있는 그림들이 이 최종 차원 벡터에다가 최근접 이웃으로 찾아낸 이미지 예시들입니다.

 이 예시의 두번째 줄에서 코끼리를 최근접 이웃 방법으로 구한 이미지들을 볼수 있어요. 하지만 탐색된 코끼리 이미지의 픽셀들은 매우 다를수 있어요. 왼쪽 면에 있는 코끼리 이미지를 사용해서 검색을 사용해보면, 이 이미지는 왼쪽에 회색 블롭 같은 형태를 가지고

...

(질문) 최근접 이웃을 이용해 어떻게 이미지를 탐색합니까?

 쿼리 이미지를 이미 학습된 알렉스 넷 분류기에 넣어서 4096차원의 벡터를 추출시키는데, 전체 테스트셋에 대해서 이 벡터들을 구한다음, 이 특징 벡터들을 L2 거리를 이용한 최근접 이웃 방법으로 탐색을 수행합니다. 이전에 본 방법들은 이 방법을 쓴건 아니지만 이렇게 구한 특징 공간으로 어떤 이미지인지 알수 있었습니다.

  특징 공간 상에서 어떤 일이 일어나는지 파악하기 위한 또 다른 방법으로 차원 축소 Dimensionality Reduction 알고리즘을 사용할수 있습니다. 여러분들이 알다시피 4096차원 벡터는 상당히 큰 차원이다보니 우리는 3차원 공간에서 살고있어 사람으로서 4096차원 특징 공간을 이해하기는 어렵겠습니다.

 우리가 해볼수 있는건 어떤 차원 축소 알고리즘을 사용해서 4096차원의 벡터를 우리가 이해할수 있는 2 혹은 3차원으로 축소시킬수가 있습니다. 다른 머신러닝 수업에서 봤을수도 있는데, 가장 간단한 알고리즘으로 주성분 분석 Principal Component Analysis가 있습니다. 이 방법은 선형 차원 축소 알고리즘으로 고차 특징 공간의 구조를 보존하길 원할때, 이 고차 벡터를 2차원으로 선형적으로 사영하는 차원 축소 알고리즘이라 할수 있습니다. 여러분이 차원 축소 알고리즘을 훈련 혹은 테스트셋으로 구한 4096차원의 벡터에 적용해서 2차원 공간 상에서 벡터를 시각화 할수 있습니디.

 딥러닝 논문에서 자주 나오는 유명한 차원 축소 알고리즘으로 t-SNE가 있습니다. 이 방법은 확률적으로 t분포를 따르는 이웃 임베딩을 구하는데(?) 자세한 사항은 넘어가고, 비선형 차원 축소 알고리즘으로 고차원의 벡터 집합을 입력으로 받아 가능한 기존의 구조를 유지하면서 2차원으로 사영시킵니다. 

 (중앙에 있는)이 시각화 결과는 10개의 mnist 숫자를 인식하도록 CNN 분류기를 학습했고, 분류기의 마지막 완전 연결 계층로부터 테스트셋 전체 이미지를 돌려 벡터들을 얻었습니다. 이 벡터는 4096차원인데, 테스트셋 각 이미지의 이 벡터를 t-sne 차원 축소 알고리즘을 적용해서 고차원의 임베딩 공간의 것을 2차원으로 축소시켜 테스트셋을 2차원 공간의 한 점으로 사영시켜 시각화하였습니다.

 다시 정리하면 이미지로부터 벡터를 계산한후 차원 축소 알고리즘으로 2차원 공간상에서의 위치를 구하였고, 이 그림에 있는 모든 각 점들은 2차원 공간에서의 숫자들의 위치이며, CNN이 학습한 전반적인 구조를 시각화 한 결과가 되겠습니다.

 여기서 놀라운 점은 10개의 숫자를 분류하였는데, 이 특징 공간 상에서 클러스터가 10개의 숫자에 맞게 10개로 나눠지는 경향이 나타납니다. 신경망을 학습시켜 얻은 특징 공간은 클래스를 인코딩 한것이지, 로 픽셀값이 아닙니다. 

  이런 비슷한 알고리즘을 숫자 인식 문제 말고 이미지 분류 문제에서도 적용할수 있습니다. 이미 비슷한 일들을 이미 해왔는데, 우선 이미지넷을 학습한 알렉스넷을 가지고와서, 테스트셋의 각 이미지의 4096차원 벡터를 추출해 냅시다. 그 다음 차원 축소 알고리즘을 적용하여 4096차원에서 2차원으로 가능한 구조를 보존하면서 줄입니다. 그러면 2차원 공간 상의 모든 점으로 사영되고, 이 2차원 공간상 점의 위치에다가 이미지를 시각화해봅시다.

 온라인에서 고해상도 버전도 볼수 있습니다. 일단 왼편의 것을 보면 이 이미지를 확대해보면 시멘틱 카테고리에따라 서로 다른영역들을 볼수 있습니다. 왼쪽이미지의 왼쪽 아래 코너를 확대해서 보면 여러가지 꽃을 볼수 있고, 오른쪽으로 평행하게 이동하면 강아지들이 있고, 오른쪽 위 코너로가면 파랗고 하얀것들을 볼수 있는데, 여기에는 배나 하늘 이미지 같은것들이 나옵니다.

  이런 시각화 방법으로 신경망이 어떻게 학습하였는지 이 공간상에서 시각적으로 볼수 있겠고, 학습된 특징 공간 상에서 어떤 종류의 이미지들이 서로서로 가까운지 볼수 있었습니다.

 이 방법을 해본 덕분에 신경망의 마지막 계층으로부터 벡터를 추출하고, 다른 종류의 연산을 해보는 방법을 고려해볼수도 있겠고, 신경망의 마지막 계층이 학습해낸 특징 공간을 다른 방법으로도 이해할수 있겠습니다.

 이렇게 하기 위해서는 트랜스포머라고 부르는 새로운 종류의 블록을 만들면 됩니다. 이 트랜스 포머 블록에서 셀프 어텐션을 사용하는데, 동작하는 과정을 보자면 우선 입력 시퀀스로 벡터 x1에서 x4까지 받습니다.

 이 전체 벡터에 대해 멀티 해드 셀프 어텐션을 동작시키고, 셀프 어텐션 연산 후에 각 출력은 각 입력과 시퀀스의 다른 원소들 사이의 상호작용으로 구해지게 됩니다. 

 셀프 어텐션 후에는 잔류 커낵션/스킵 커낵션을 시키고,

 그 뒤에는 레이어 정규화 층을 추가하겠습니다. 이 방법은 심층 신경망에서 정규화 하는 기법 중 하나로 최저과 과정을 도우며, 합성곱 신경망에서는 주로 배치 정규화가 사용되고, 시퀀스 모델의 경우 레이어 정규화가 유용하게 사용됩니다.

 레이어 정규화에 대해서 흥미로운 점은 셀프 어텐션의 출력으로 벡터들의 집합이 만들어지는데, 레이어 정규화는 벡터들 사이에 상호작용이나 어떤 연산없이, 셀프 어텐션의 출력 벡터들이 각각 독립적으로 정규화가 되어 벡터들간의 어떤 작용이 존재하지가 않습니다.

 레이어 정규화를 한 후에는 순방향으로 다층 퍼샙트론 연산을 하겠습니다. 다른 말로 완전 연결 신경망이라고도 부르는데, 레이어 정규화의 출력은 벡터들의 집합으로 이들을 완전 연결 신경망에 전달하여, 이들을 각 시퀀스별로 독립적으로 연산하겠습니다.

 그 다음에는 다층 퍼샙트론 연산들에 대해서 별도의 잔류 커낵션을 추가하고,

 또 다른 레이어 정규화 계층을 추가 하겠습니다.

 이들을 한 블록에다가 모은걸 트랜스포머 블록이라 합니다. 이 블록은  벡터 시퀀스를 처리하는 큰 규모의 모델을 만드는데 사용할수 있겠습니다.

 이 트랜스포머 블록의 입력으로 벡터 x의 집합이고, 출력은 벡터 y들의 집합으로 입력 벡터와 개수와 출력 백터의 개수는 동일합니다. 하지만 출력 벡터는 다른 차원수를 가질거에요. 이러한 벡터의 차원은 모델 내부에서 바꿀수 있겠습니다.

  이 셀프 어텐션/트랜스포머 블록의 흥미로운점은 셀프 어텐션 부분에서만 벡터들간의 상호작용이 일어난다는 점인데, 레이어 정규화와 다층 퍼샙트론에서는 각 벡터들이 독립적으로 연산되기 때문입니다. 이 블록의 이러한 장점 덕분에 트랜스포머 블록은 매우 병렬화 하기 좋고, GPU 하드웨어에서 다루기가 좋아 학습하기에 매우 좋습니다.

 그러면 이제 트렌스포머 블록의 시퀀스로 사용해서 트랜스 포머 블록을 만들어봅시다. 트랜스포머 모델을 만들려면 하이퍼 파라미터들을 선전하여야 합니다.

 하나는 모델의 깊이로 블록의 갯수인데, "Attention is all you need" 논문에 있었던 블록의 개수는 12개를 사용하였고, 각 플록의 쿼리 차원을 512차원으로 지정하였고, 6개의 멀티 해드 어텐션 레이어를 사용하였습니다. 여기서 멀티 해드 어텐션은 셀프 어텐션 연산에서 수행되요.

 이 트랜스포머 아키텍처를 "Imagenet moment for natural language procesing"이라고 부르며, 자연어 처리에서 매우 유용하게 사용되고 있습니다. 여러분도 알다시피 컴퓨터 비전에서 이미지냇으로 선학습 시키고, 특정 작업 용도로 미세 조정하는게 흔하다 시피, 트렌스포머 모델도 수 많은 시퀀스 예측이나 자연어 작업에서 비슷한 효과를 보입니다.

 지금 보는 이 내용들은 아주 최근 연구 결과들로, 작년에 있었던 논문에서는 아주 큰 트랜스포머 모델을 인터넷에서 아주 많은 양의 텍스트를 다운받아 다음에 올 단어를 예측하거나 다른 자연어 처리 모델 동작을 할수 있도록 선학습을 시킬수 있고, 기계 번역이나 언어 모델링 혹은 언어 생성이나 질의응답 등 어떤 작업을 하던간에 자연어 처리와 관련된 어느 작업이든 미세조정을 할수 있습니다.

 몇 강의 전에 이미지넷 대회에서 이런 전이학습 트랜드가 나타났던처럼 작년(이 강의 발표 기준 2018년같음)부터 트렌스포머 모델을 이용해서 비슷한일이 벌어지고 있습니다.

 최근 큰 인공지능 연구소에서 훨씬 큰 트랜스 포머 모델을 만들려고 연구중이며, 기본적인 모델로 2017년 "attention all you need" 어텐션 논문에 나온 transformer base과 transfomer large 모델이 있습니다. large 모델은 213만개 학습가능한 파라미터를 가지고 있어, 8개의 GPU로 학습하는데 3.5일이 걸렸다고 합니다.

 다음 논문은 BERT라고 하는 모델로 선학습하고, 미세조정 과정을 거친 모델로 340백만개의 학습가능한 파라미터를 가지며 더 커지고, 13GB의 텍스트로 학습하였습니다. 텍스트 자체는 작지만, 13GB의 텍스트는 아주 큰 데이터이고, 논문에서 훈련 시간이나 하드웨어를 설명을 찾을수가 없었습니다.

 구글의 다른 그룹과 페이스 북에서 만든 모델로 XLNet-Large와 RoBERTa가 있는데, 이 모델들은 100GB 이상의 데이터를 학습하였으나 빠르게 학습하였습니다. 구글의 모델은 512TPU 디바이스-v3로 2.5일간 학습하였고, 페이스북의 모델은 1024개의 GPU로 하루를 학습시켰습니다.

 Open AI에서 그동안의 한계를 뛰어넘은 모델을 발표했는데, 자체 생성한 40GB 텍스트로 15억개의 학습한 파라미터를 가진 트랜스포머 모델을 학습하였습니다. 모델 자체는 동일하나, 다른 부분은 더 많은 레이어와 각 셀프 어텐션 레이어에서 더 많은 쿼리 차원을 가지고, 더 많은 셀프 어텐션 레이어를 사용한다는 점입니다. 모델 자체는 근본적으로 동일하고, Open AI에서 가지고 있는 이 모델을 GPT2라고 합니다.

 셀프 어텐션 레이어는 신경망에서 사용할수 있는 새로운 종류의 레이어로, 셀프 어텐션 레이어를 사용한 합성곱 신경망을 만든 예시를 살펴보자.

 이 합성곱 신경망은 귀여운 고양이 이미지를 입력으로 받아 합성곱 레이어들의 출력으로 어떤 벡터의 그리드 c x h x w, 가로 h, 세로 w, 채널 수가 c인 출력을 만들어낸다. 

 그러면 이제 세개의 1 x 1 합성곱 연산을해서 특징 그리드들을 쿼리들의 그리드, 키의 그리드, 값의 그리드들로 변환하자. 각 1 x 1 합성곱 연산들은 학습 과정으로 얻은 고유의 가중치와 편향값을 가지고 있어, 병렬로 분할시킨다.

 이제 쿼리와 키를 내적 한 뒤 소프트 맥스 함수를 적용하여 어텐션 가중치를 구할건데, 이 결과는 입력 이미지에서 한 지점이 주어질때 이에 대해 다른 모든 지점들은 얼마나 주의를 기울여야 하는 정도를 나타낸다. 그렇다보니 크기가 (h x w) x (h x w)의 아주 큰 어텐션 가중치 행렬이 만들어진다.

 이 어텐션 가중치를 값 벡터들과 선형 결합을 시키겠다. 이 선형 결합으로 새로운 특징 벡터의 그리드를 만들어 내고, 그 출력 그리드의 모든 위치들은 입력 그리드의 모든 위치에의해 정해진다/영향을 받겠다. 이 과정은 기존의 합성곱과 상당히 다른 연산과정이라 할수 있겠다.

 실제 사용시에 종종 사람들은 이 어텐션 연산을 마친 후에 추가적인 1 x 1 합성곱 연산을 하기도 하고, 

이 셀프 어텐션 연산 전체 주위로 잔류 연결/스킵 커넥션을 추가하는 경우도 많습니다. 그래서 이런 요소들을 한데 합쳐서 새로운 셀프 어텐션 모듈을 만들어서 신경망에다가 넣어서 사용할수 있고, 이렇게 만든 신경망은 합성곱 연산 뿐만 아니라 더 셀프 어텐션을 할수 있겠습니다.

  여기서 기본적으로 다뤄보면 좋은 것으로 신경망에서 벡터의 시퀀스를 처리하는데 사용할수 있는 방법으로 3가지가 있습니다. 가장 흔한 방법은 이전 강의에서 다루었던 순환 신경망이 있는데, 입력 벡터들의 시퀀스 x가 주어지면, 출력 벡터 y의 시퀀스를 만들어 내었습니다.

 LSTM과 같은 순환 신경망을 사용할때 좋은점은 아주 긴 시퀀스를 다루는데 좋은것으로, 아주 긴 시퀀스에서도 정보를 잘 전달할수 있습니다. 특히 RNN 레이어의 최종 출력 혹은 최종 은닉 상태 y_t는 전체 입력 시퀀스로 구하게 되요. 단일 rnn 레이어는 전체 입력 시퀀스를 요약한 것이라고 볼수 있겠습니다.

 하지만 RNN은 몇가지 문제점을 가지고 있는데, 이들을 은닉 상태 1을 계산한다음 2를 계산하고, 3을 계산하고, 4를 계산하는 데이터에 순차적으로 의존적이라 병렬화 시키기가 어렵습니다.

 이전에 gpu 강의를 다시 떠올려보면, 아주 큰 신경망을 만들때 GPU의 방대한 병렬 연산의 이점을 가질수면 좋겠지만 RNN은 그런 하드웨어로 병렬 연산을 하는데 좋지 않아 큰 RNN 모델을 만드는데 문제가 있습니다. 

 또 다른 시퀀스를 처리하는 방법으로 일차원 합성곱 연산이 있습니다. 일차원 합성곱 연산을 입력 시퀀스에 대해서 슬라이드 시켜, 출력 시퀀스의 각 지점들은 입력 시퀀스의 세 이웃으로 구할수 있겠습니다.

 컨볼루션을 이용하여 시퀀스를 처리하는 신경망의 경우, RNN이 순차 의존성을 가지넋과는 달리 시퀀스의 각 출력 원소들이 독립적으로 계산되다보니 매우 병렬화하기 좋은 점을 가지고 있습니다. 

 하지만 합성곱 연산을 이용한경우 단점은 매우 긴 시퀀스를 잘 처리하지 못한다는 점인데, 출력을 전체 시퀀스로 구하고자 하는경우, 단일 합성곱 레이어로는 구할수 없으며 시퀀스의 모든 지점을 보기 위해서 아주 많은 레이어를 쌓아야 합니다. 그런 이유로 합성곱으로 시퀀스를 처리하기는 어려우나, 병렬화하기 좋다는 장점이 있습니다.

 이번에 다뤄볼 방법으로 셀프 어텐션이 있습니다. 이 방법은 앞서 본 결점들을 극복한 시퀀스나 벡터의 집합을 처리할수 있는 새로운 메커니즘으로, 셀프 어텐션은 주어진 벡터의 집합으로 각 벡터와 다른 모든 벡터들을 비교하다보니 긴 시퀀스를 잘 처리할수 있습니다. RNN과 비슷하게 단일 셀프 어텐션 레이어는 각 출력들은 각 입력에 영향을 받겠습니다.

 뿐만아니라 셀프 어텐션은 합성곱 연산과 같이 매우 병렬화 하기 좋다는 장점을 가지고 있습니다. 몇  슬라이드 전에 본 셀프 어텐션 구현 과정을 보면, 셀프 어텐션은 크지만 몇개의 행렬 곱 연산에다가 소프트 맥스 같은게 추가되다보니 아주아주 병렬화 하기가 좋으며, GPU에서 연산시키기에 적합하다고 할수 있겠습니다.

 셀프 어텐션은 합성곱과 순환 신경망의 단점을 극복하여 시퀀스나 집합을 처리할수있는 대안 메커니즘으로 사용되고 있습니다. 하지만 단점으로는 아주 많은 메모리 공간을 사용한다는 점이나 시간이 갈수록 GPU 메모리 공간이 더 커지고 있으므로 이런 문제는 무시해도 되겠습니다.

  여러분들이 신경망으로 시퀀스를 처리하다가 어떤 문제를 만날떄, rnn, 컨볼루션, 셀프 어텐션중에서 어떤걸 사용하느게 좋을까요? 몇년 전에 있었던 한 유명한 논문으로 "Attention is all you need"가 있으며, 셀프 어텐션 만으로도 시퀀스를 처리하는 신경망을 만들수가 있겠습니다.

 이번에 다뤄볼 것은 어텐션 레이어의 특별한 케이스로 셀프 어텐션 계층이 있습니다. 셀프 어텐션 계층은 입력 벡터 집합 하나만을 사용하는 것인데, 우리가 할일은 각각의 입력 벡터 셋에 있는 각각의 입력 벡터를 다른 입력 벡터와 비교하겠습니다. 이걸 위해서 우리가 할 작업은 또 다른 학습 가능한 가중치 행렬을 추가하는것인데,

 쿼리 벡터들을 입력으로 사용하는것이아니라, 쿼리 벡터들을 입력 벡터들을 변환시켜 추정해냅니다. 그다음에는 이전에 본것과 동일하게 동작합니다. 이 과정이 어떻게 동작하는지 그림으로 보자면 오른쪽에 입력 벡터 x1, x2, x3의 집합을 입력으로 받습니다.

 이번에는 각 입력 벡터를 쿼리 행렬과 곱하여 쿼리 벡터로 변환시키겠습니다.

 그러고나서 비슷하게 입력 벡터를 키 행렬을 사용해서 키 벡터로 바꾸고,

 각 키 벡터와 각 쿼리 벡터 사이의 배정 스코어를 계산할수가 있겠습니다. 이 배정 스코어는 입력 시퀀스 x의 각 입력끼리의 쌍간의 유사도라고 할수 있겠습니다.

 이제 이전과 똑같이 소프트맥스 함수를 사용해서 각 컬럼방향으로 확률 분포를 구해내고,

 입력 벡터들을 값 벡터로 변환시키겠습니다.

 그러고나서 값 벡터와 가중화된 유사도를 구하고, 출력 벡터 y 집합을 만들어내겠습니다. 이 과정이 전반적인 메커니즘이라고 할수 있겠습니다.

 지금까지 한것들 전체가 새로운 종류의 신경망 레이어라고 할수 있는데, 벡터 집합을 입력으로 받아 벡터 집합을 출력하는데다가, 내부적으로 하는 일은 입력에서의 한 벡터를 다른 각 벡터들과 비교하게되며 신경망은 스스로 어떤 비선형 함수를 사용할지 결정합니다.

 셀프 어텐션 레이어의 놀라운 점은 우리가 입력 벡터의 순서를 바꾼 경우에 볼수 있는데, 입력 벡터를 같은 것들을 가지고 있으나 1, 2, 3 순서가 아니라 3, 1, 2로 하는경우 어떤 일이 일어날까요.

그렇더라도 동일한 키 벡터들과 동일한 쿼리 벡터들을 구할수 있겠습니다. 키 벡터와 쿼리 벡터는 서로 서로 영향을 주지 않기 때문입니다. 다만 정확하게 같은 키 벡터와 쿼리 벡터를 구할수 있지만 입력 벡터의 순서대로 뒤바뀌겠습니다.

 다음으로 뒤바뀐 벡터들 사이의 유사도 스코어들을 계산할때, 모든 유사도 스코어는 동일하지만 행과 열이 바뀌었기때문에 이 행렬 자체도 뒤바뀌어 있겠습니다. 하지만 값 자체는 동일해요. 

 이전과 비슷하게 어텐션 가중치를 계산할수 있겠고, 값 자체는 동일하나 여전히 뒤바뀌어 있겠다.

 값 벡터들 자체도 동일하나 뒤바뀌어있고,

 출력 벡터도 동일하지만 뒤바뀌어있다.

 이 현상이 무엇을 의미하냐면 기술적으로 이야기하면 셀프 어텐션 계층, 셀프 어텐션 연산은 동등 치환 permutation equivalent(동일하나 순서를 바꾼다?? 정도로 이해)이며, 이 동등 치환이라는 것은 우리가 입력 벡터 x를 치환 연산 s를 적용한 다음에 출력을 계산한 것 f(s(x))과 치환/변환?하지않은 입력으로 결과를 구한뒤 치환시킨것 s(f(x))이 동일하다는 의미가 되겠습니다.

 그리고 셀프 어텐션 레이어를 다른 방향으로 고민해보자면, 이 셀프 어텐션 레이어는 입력의 순서를 신경쓰지 않습니다. 순서를 고려하지 않는 다는 점에서 새로운 종류의 신경망 계층이기도 하며, 벡터의 집합만을 가지고 연산하겠습니다.

 셀프 어텐션 레이어가 하는건 여러 벡터들 x을 가지고 각 벡터들 q, k을 서로 서로 비교해서 새로운 벡터 집합 y을 구하는 일을 하겠습니다.

그래서 이 레이어는 입력 벡터를 처리할때 그 벡터들의 순서가 어떻게 되는지 잘 모르겠습니다. 하지만 벡터들의 순서를 알아야하는 경우도 있을거에요 예를 들자면 번역이나 캡셔닝 작업같은 경우에는 시퀀스를 생성하고, <end> 토큰으로 마무리 합니다.

 이와 같은 어떤 작업들의 경우 모델이 벡터가 어느 위치에 있는지 아는게 중요한 경우도 있습니다. 하지만 셀프 어텐션 레이어는 동등 치환이다보니, 어떤 벡터가 첫번째인지 어느것이 맨마지막인지 알 방법이 없습니다. 

 그렇지만 각 입력 벡터에 위치 인코딩을 함으로서 위치 이동에대한 민감도를 절반정도 복원시킬수가 있습니다. 이걸 구현하는 다양한 방법들이 있는데 이들 중 한 방법은 룩업 테이블을 학습하는 방법입니다.

 이 신경망에다가 학습가능항 가중치 행렬을 추가시키는것인데, 벡터 하나로 첫번째 위치를 학습하고, 다른 한 벡터로 두번쨰 위치를 학습하고, 다른 벡터로 세번쨰 위치를 학습하겠다. 그러고나서 신경망 순전파 연산을 수행할때에는 첫번째 벡터 아래에다가 학습한 위치 벡터를 붙이고, 두번째 입력 벡터  신경망 순전파를할때, 첫번째 벡터 아래에 학습된 위치 벡터를 붙이고, 두번째 위치 벡터를 붙이고 그런식으로 가겠다.

 이렇게 함으로서 모델은 시퀀스의 파트들이 시작부분인지, 끝부분인지 구분할수 있게 되었으며 이것을 위치 인코딩 positional encoding이라고 부르며, 이것들이 가끔 셀프 어텐션 모델에서 사용되는걸 볼수 있겠다.

 다른 셀프 어텐션 레이어의 변형으로 마스크 셀프 어텐션 레이어라고 부르는 방법이 있는데,

 이 방법을 정리하자면 어떤 작업들을 할때 모델이 이전의 정보만 사용하기를 원할때, 순환 신경망은 은닉 상태가 진행하도록 설계된다는점을 떠올려보면 언어 모델 같은걸 모델링할시, 이전의 모든 토큰이 주어질때 다음 토큰을 추정할겁니다.

 디폴트 셀프 어텐션 레이어를 사용하면 모든 출력 벡터를 만드는 과정에서 모든 벡터를 사용하게 될건데, 언어 모델 같은 종류의 작업에서는 잘 동작하지 않게 될겁니다. 하지만 이문제는 어텐션 매트릭스에 어떤 구조를 추가해서 고칠수가 있습니다.

 예를들어 모델이 과거 정보만 사용하도록 강제로 만들려면, 이 추정 행렬 e에서 집중하지 않아야하는 모든 위치에다가 -무한대를 넣으면 됩니다. 그래서 이 예시에서 첫번째 입력과 q1에 대한 출력 벡터를 만든다고할때, 첫번째 출력은 첫번째 입력으로만 구하면되겠습니다.

 그래서 이런 과정을 행렬에다가 음의 무한대를 넣어서 할수 있고, 소프트맥스 함수로 계산하면 -무한대는 어텐션 가중치로 0의 값을 들을 가지게 되겠습니다. 이런 구조를 마스크화된 셀프 어텐션 레이어라고 부르며, 출력을 생성할때 입력 일부만 보도록 마스크시켜주는 역활을 하기 때문입니다.

 이 구조가 언어 모델 작업과 같이 모델이 이전 단어들만 사용해서 다음 단어를 추정해야하는 언어 모델 작업과 같은곳에서 자주 사용됩니다.

  이러한 셀프어텐션 레이어의 또 다른 버전으로 멀티 해드 셀프 어텐션이 있습니다. 이 방법은 해드의 개수 h를 지정하고, 셀프 어텐션 레이어를 병렬로 독립적으로 동작시킬건데 여기다가 입력 벡터를 분할해서 주는데, 입력 벡터 x가 d 차원이라면 각 입력 벡터들을 동일한 h개의 덩어리로 분할시켜주겠습니다.

 이 각각의 입력 벡터 덩어리들을 병렬화된 셀프 어텐션에다가 각각 넣어주고, 각 하부 셀프 어텐션레이어는 각 입력에대해서 각 출력들을 만들어낼것이고, 이러한 멀티해드 셀프 어텐션 레이어로부터 최종 출력을 얻기위해서 이 각 출력들은 연결시키겠습니다.

 이 멀티해드 셀프어텐션 레이어는 실제로도 자주 사용되고 있으며, 여기서 기본적으로 두 하이퍼파라미터를 가지는데 하나는 쿼리 벡터의 차원과 우리가 추정하고자하는 출력 y의 최종 차원가 있겠습니다. 이번에 이 모델에서 내부적으로 우리가 지정해주어야하는 두 하이퍼 파라미터로 하나는 내부 키 벡터 Dq의 차원과 다른 하나는 해드 h의 갯수가 되겠습니다.

 이 값 둘다 실제 셀프 어텐션 레이어들을 사용하는걸 볼때 볼수 있으며, 사람들이 각 레이어의 전반적인 폭지정해둔것을 볼수 있는데 이건 쿼리벡터 Dq의 차원이며, 셀프 어텐션 레이어의 해드 갯수 h를 지정한것을 볼수 있겠습니다.

 지금까지 어텐션 메커니즘으로 다양한 작업들에 사용한 경우들을 알아보았습니다. 하지만 최근 몇 년간 연구에서 어떤 일들이 있었을까요? 많은 작업에서 유용해보이다보니 이 메커니즘을 다양한 타입의 문제에서 적용시키기위해서 추상화하고 일반화시키고 싶을수 있겠습니다.

 이 어텐션 매커니즘의 개념들로부터 시작해서 이전에 이미지 캡셔닝과 기계 번역에서 사용했었는데,이 개념들을 일반화하여 순환 신경망이나 다른 만든 신경망에다가 범용 목적의 계층으로서 넣어 사용할수있겠습니다. 

 우리가 보아온 어텐션 매커니즘을 재정립하기위한 방법은 쿼리 벡터 q와 (출력의 매 타임 스탭마다 은닉 상태 벡터로 구한)이전 어텐션을 입력으로하고, 거기다가 어텐드를 하고자하는 은닉 벡터를 구하는데 필요한 입력 백터의 컬랙션 x을 사용합니다. 또, 유사도 함수 f_att를 사용해서 쿼리 벡터와 입력 벡터로 된 데이터베이스에서 각각의 것들을 비교하게 되요.

 아래의 내용이 우리가 여러번 보아온 어텐션 메커니즘의 계산 과정인데, 이 연산에서 유사도 함수 f_att로 쿼리 벡터와 각 입력 벡터 사이의 유사도 벡터들을 만들어내요. 이 값들은 정규화되지않은 유사도 스코어다보니 소프트맥스 함수를 사용해서 각 입력 벡터 x에 대한 확률 분포로 정규화 시키겠습니다. 출력은 단일 벡터 y로 입력 벡터 x들의 가중화된 선형 결합으로 구합니다.

 일반화를 위한 첫번째 과정으로 유사도 함수 similarity functino을 바꿔봅시자. 이전에 만든 유사도 함수 f_att는 초기 어텐션 논문에서 사용되었던 것인데, 유사도 함수에서 사용되는 벡터들간의 점곱 dot product로 더 효율적으로 구할수 있다는것이 밝혀졌습니다.

 이 방식으로 간소화 시키겠습니다. 이렇게함으로서 신경망의 유사도들을 일일이 계산하기보다는 모든 유사도를 행렬 곱의 형태로 더 효율적으로 계산 할수 있겠습니다.

 조금더 자세히 들어보자면 사람들은 그냥 점 곱 연산을 사용하기보다는 유사도 스코어를 계산하는데 조정된 점곱 연산 scaled dot product라고 부르는 방법을 사용합니다. 

 이 방법은 쿼리 벡터 q와 입력 벡터들중 하나인 x_i로 유사도 스코어를 구할때, q와 x_i를 점곱해주고 이 결과를 sqrt(D_q)로 나누어줍니다. 여기서 D_q는 쿼리벡터의 차원이 되겠습니다.

 이 연산을 하는 이유를 정리하자면 우리는 구한 유사도 스코어를 소프트맥스 함수에다가 적용시킬건데, 소프트 맥스 함수에 들어오는 입력이 너무 크다면 그라디언트 소멸 문제가 생기게 됩니다. 한번 어텐션 가중치 e_i가 다른것들보다 훨씬 크다면, 하나만 아주 큰 소프트 맥스 확률 분포가 나올것이고 모든 지점의 그라디언트가 0에 가까워지게 만들어 학습을 어렵게 할겁니다.

 또 다른 문제로는 아주 고차원 벡터를 다루는 경우에 접 곱을 구하면 크기도 아주 커지게 되겠습니다. 두 벡터 a, b의 접곱을 계산하는 구체적인 예시를 보면 둘다 같은 차원 d인데, 이 두 벡터의 점 곱은 두 벡터 크기를 곱한것에다가 두 벡터 사이 각도에 대한 코사인를 곱해주면 되겠습니다.

 한번 우리가 두 상수 벡터를 가지고 있다고 하고, 두 벡터 중 하나의 크기 magnitude는 그 벡터의 차원의 제곱근으로 조정시키겠습니다. 이는 우리가 아주 긴 차원의 신경망을 다룬다고할때, 아주 긴 차원 벡터를 가지고 점곱을하게될것이고, 그러면 아주 큰 값이 나오게 될것입니다.

 그래서 이를 상쇄하기위해서 점곱에다가 차원의 제곱근으로 나누어주어, 점곱 결과는 차원의 크기에 따라 조정되겠습니다. 이렇게 하면 소프트맥스 함수를 통과한 후에도 더 나은 그라디언트를 가지게 됩니다.

  다음 일반화 방안으로 다중 쿼리 벡터를 사용하겠습니다. 지금까지 본 것들은 디코더의 각 타임 스탭마다 하나의 쿼리 벡터를 가지고 사용하였습니다. 쿼리 하나를 가지고, 입력 벡터들 전체에 대한 확률 분포를 생성하는데 사용했어요. 

 이제는 이 어텐션이라는 개념을 여러 쿼리 벡터의 집합을 가지고 일반화를 시켜봅시다. 입력으로 쿼리 벡터 집합 q와 입력 벡터의 집합 x를 가지고 있고, 각 쿼리벡터로 전체 입력벡터 각각에 대한 확률 분포를 생성해낸다고 합시다. 그러면 이들 끼리의 유사도를 다 계산할수 있을거에요.

 우리는 각 쿼리벡터와 각 입력 벡터 사이의 유사도를 계산해야하는데, 조정된 점곱 연산으로 유사도 함수를 사용하여 단일 행렬곱 연산으로 전체 유사도 스코어들을 동시에 계산할수가 있겠습니다. 여기서 기억하고 있어야될것은 우리는 각 쿼리 벡터에대한 입력 벡터들의 확률 분포를 계산해야하는데, 출력된 어텐션 스코어의 (쿼리 벡터에 대한) 한 0차원에다가 소프트 맥스 함수를 적용시켜서 구할수가 있어요.

  출력 벡터를 생성시키기 위해선, 이전에는 하나의 출력벡터를 구했지만 지금은 쿼리 벡터 집합을 가지고 하다보니 각 쿼리 벡터에 대한 각 출력을 만들어야 되겠습니다. 쿼리 q_i에 대한 출력 백터는모든 입력 백터의 가중화된 결합으로 구할수가 있는데, 여기서 쿼리벡터로 추정한 확률 분포로 가중을 주었습니다.

 이러한 연산을 행렬 형태로 다룰수가 있는데, 추정한 어텐션 가중치 A와 입력 벡터들 X 사이의 하나의 행렬곱 연산으로 이 모든 선형 결합을 동시에 계산할수가 있습니다.

 다음 일반화 방안은 입력 벡터를 사용하는 방법에 관한것인데, 이 슬라이드를 보면 입력 벡터들을 두가지 방향으로 사용하고 있습니다. 하나는 입력 벡터들을 각 쿼리 벡터와 함께 어텐션 가중치를 계산하는데 사용해요. 그 다음으로는 입력 벡터들을 다시 출력을 계산하는데 사용하고 있습니다.

 이들은 실제로는 우리에게 필요한 서로 다른 두 함수(유사도 계산 함수와 출력 벡터 계산 함수)라고 할수 있어요. 그래서 입력 벡터를 키 벡터와 입력 벡터로 나눌수가 있는데, 우리가 하고자하는건 입력으로 그대로 쿼리 벡터 집합 q와 입력 벡터 집합 x를 가지고는 있으나, 입력 벡터들을 그대로 서로 다른 두 함수안에서 사용하는게 아니라

 학습가능한 키 행렬 W_k와 학습 가능한 값 행렬 W_v를 사용해서 입력 벡터를 키 벡터의 집합과 값 벡터의 집합으로 변환 시킬수가 있겠습니다. 이제 이 두 키 벡터들과 값 벡터들을 이 어텐션 계층의 연선에서 서로 다른 두 용도로 사용하면 됩니다.

 이제 우리가 할일은 유사도 스코어를 계산하는데 각각의 쿼리 벡터와 각 키 벡터를 계산하면 되고, 출력 스코어를 계산할 시에 출력들은 가중화된 값 벡터, 그러니까 값 벡터들을 추정한 유사도 스코어로 가중화한 것으로 구할수가 있겠습니다. 

 이걸 정리하자면 이 과정을 통해서 모델은 입력 데이터를 어떻게 사용할지 더 유연하게 고려할수 있게 됩니다. 왜냐면 쿼리 벡터는 모델에게 전달하는 내가 찾고싶다고 알려주는 것인데, 이미 알고있는것과 다른 정보를 다시 돌려받을 필요가 있어요.

 이 과정은 구글에서 검색하는 과정과 비슷하다고 할 수 있는데, "how tall is the empire state building", "엠파이어 스테이트 빌딩이 얼마나 높은가요?"라는 쿼리/질문을 하면, 구글은 이 쿼리랑 수 많은 웹 패이지들을 비교하고, 여러 웹 페이지를 전달해줄거에요.

 하지만 쿼리 자체는 이미 알고 있으니 우리가 쿼리랑 웹 페이지가 얼마나 잘 일치하는지 관심 가질 필요는 없고, 그보다는 찾은 데이터가 쿼리와 연관된 것인지 알고싶을 겁니다. 그래서 웹 검색 어플리케이션에서 "엠파이어 스테이스 빌딩이 얼마나 높은가요"라는 쿼리로 검색하면, 우리 원하는 데이터는 쿼리로 얻은 텍스트에 있는 몇 미터나 되는지에 대한 데이터들 일거에요.

 그래서 명확하게 하자면 키 벡터와 값 벡터로 나눔으로서 모델이 입력을 두가지 방법으로 사용할수 있도록 더 유연하게 만들겠습니다.

 이건 꽤 복잡한 연산인데, 이 슬라이드로 이 연산과정을 시각화 시켜 보겠습니다. 바닥에 쿼리 벡터 집합으로 q1에서 q4까지 있고, 왼편에 입력 벡터의 집합으로 x1에서 x3까지 있습니다.

 첫번째로 할 일은 각 입력 벡터들을 키 행렬과 연산을하여 각 입력에 대한 키 벡터들을 만들어 냅시다. 

 이제 이 키 벡터를 각각의 쿼리 벡터와 비교를 하여 정규화되지 않은 유사도 스코어의 행렬을 만들수가 있어요. 이 유사도 행렬의 각 원소들은 키 벡터 하나와 쿼리 벡터 하나 사이의 조정된 점곱 연산한 값이 되겠습니다.

  다음으로 할 일은 이 어텐션 스코어는 정규화되지 않았다보니 각 쿼리 벡터에 대해서 확률 분포로 만들어내겠습니다. 소프트 멕스 연산을 이 배정 행렬 E의 수직 차원으로 수행함으로서, 배정 스코어 A를 구하였습니다. 여기서 소프트 맥스 함수를 수직 방향으로 하다보니 배정 행렬의 각 컬럼은 입력 x1, x2, x3에대한 확률 분포가 되겠습니다.

다음으로 할일은 지금까지 배정 스코어를 구하는 과정을 거쳤고, 이제 출력을 계산하기 위해서는 입력 벡터들을 값 벡터로 변환을 시켜야 합니다. 각 입력 벡터를 보라색 상자의 값 벡터 v1, v2, v3으로 만들겠습니다.

   그러고나서는 배정 스코어를 이용하여 값 벡터들을 가중화 선형 결합을 하겠습니다. 예를 들자면 V1을 행방향으로도 곱하고, 열방향으로도 곱하고 합 연산을 합니다. 이 말을 정리하자면 V1은 A11과 곱하고, V2는 A12와 곱하고, V3은 A13과 곱한뒤 합을하여 위로보내게 됩니다.

 각 값 벡터들은 해당하는 열 값과 곱하고, 이들을 합을 해서 올림으로서 각 쿼리벡터 q에 대한 출력 벡터 y를 만들어내게 됩니다.  이러한 출력 벡터 y는 가중화된 값 벡터들의 선형 결합니고, 가중의 정도는 키 벡터와 쿼리 벡터 사이의 점곱으로 계산하였습니다.

 이게 어텐션 레이어이고, 신경망에 삽입할수 있는 가장 일반적인 형태가 되겠습니다. 이건 우리가 두 데이터셋을 가진 경우, 하나는 쿼리로 보고, 다른 하나는 입력으로 보면, 이 어텐션 계층에 입력으로 사용하여 쿼리와 입력간의 결합 함으로서 계산할 수 있겠습니다.

 이 슬라이드 왼편을 보면 고양이 이미지를 입력으로 받는다고 하고, 합성곱 신경망을 돌려보겠습니다. 그러면 이 합성곱 신경망의 마지막 합성층의 출력을 격자로 된 특징 백터로 볼수 있습니다. 그러면 다음 이미지도 격자로된 특징 벡터를 얻을수가 있으며 각 격자 특징 벡터들은 이미지의 공간적 위치에 해당한다고 볼수 있겠습니다.

-> 격자 특징 벡터 하나 하나는 이미지의 어느 위치에 대한 특징 계산 결과임.

 다음으로 할일은 시퀀스 모델에서 했던것 처럼 어텐션 매커니점을 적용시켜볼건데, 은닉 상태로 그리드 벡터를 사용해서 디코더의 초기 은닉 상태 s0를 추정하겠습니다. 그러면 이제 디코더는 초기 은닉 상태 s0를 비교함수 f_att로 격자 특징의 모든 위치와 초기 은닉 상태 s0 사이의 쌍 배정 스코어 pairwise alignment score를 계산하는데 사용하겠습니다.

 모든 출력 결과는 스칼라 값이 나올것이고, 이 값은 해당 벡터 부분을 크게 중요하게 본다면 크고, 해당 벡터 부분을 덜 중요하게 본다면 낮은 값을 가지게 됩니다. 이런식으로 격자/그리드 배정 스코어를 얻을수가 있어요. 그래서 배정 스코어에 대한 그리드의 각 원소는 다시말하면 하나 하나가 f_att로 구한 스칼라값이 되겠습니다.

 그래서 이렇게 격자 어텐션 스코어를 구하였으면 이들을 확률 분포로 정규화해주기위해 소프트 맥스 함수를 사용하겠습니다. 이 결과는 출력 캡션의 첫번째 단어를 만들어낼 때 입력 이미지의 모든 위치에서 모델이 어느 부분에 집중을하였는지를 확률 분포로 나타내게 됩니다.

 그러면 이제 가중화된 은닉 벡터를 사용할건데, 어텐션 확률 스코어와 격자 벡터를 선형 결합을 시켜서 구할수가 있고 이 값이 첫번째 컨텍스트벡터 c1이 되겠습니다.

 이 컨텍스트벡터는 출력 시퀀스의 첫번째 토큰을 만드는데 사용할것이며, rnn 디코더 1층을 지나가면서 첫번째 단어로 cat을 만들어 냅니다.

 이제 다음으로 넘어가서 이 과정을 다시 반복하겠습니다.

 이번에는 (디코더의) 다음 은닉 상태인 s1을 격자 특징의 모든 지점과 비교하는데 사용해서 새 배정 스코어 격자를 만들어내고,

소프트맥스로 정규화시켜 이미지 전체 위치에 대한 확률 분포를 만들어 냅니다.

 그러면 이것으로 디코더의 두번째 타임스탭에서 사용할수 있는 새 컨텍스트 벡터를 구할수가 있겠고,

이걸로 다음 단어를 만드는데 사용하겠습니다.

 이미지에 있는 내용들을 계속 순방향으로 정리해가면서 캡션 "cat sitting outside <stop>"을 만들어 냅니다. 지금 본 이 구조는 시퀀스 투 시퀀스로 번역했을때 경우와 매우 비슷한 구조인걸 알수 있습니다. 그래서 이 덕분에 모델이 입력 이미지의 격자 특징을 가중치를 주며 재조합을하여 새 컨텍스트백터를 생성할수 있게 만들었습니다.

 한번 이 새 이미지에 대해서 한번 고민해보면, 이 모델은 새 이미지를 입력으로 받고 있고 출력으로 단어 시퀀스 "a bird is flying over a body of water"를 만들어 내고 있다.

 출력 시퀀스를 만들어내는 모든 타임 스탭에서 모델은 어텐션 가중치들을 추정하며, 합성곱 신경망으로 입력 이미지를 처리하여 얻은 격자 특징의 위치들에 대한 확률 분포를 알려준다.

 모델이 "bird flying"이란 단어를 추정해낼때 모델은 입력 이미지에서 새에 집중하고 있으며, "water"라는 단어를 추정할때는 어텐션 가중치가 새를 제외한 나머지 부분들 수면에 집중하는걸 볼수 있겠습니다.

 왜 이런 매커니즘을 이미지 캡셔닝에서 사용해야하는지를 정리하자면 생물학적으로 생각해보면 좋겠는데, 왼쪽의 사람 눈 그림을 보자. 사람의 눈은 원형이고, 한쪽 면에는 빛이 들어올 수 있는 렌즈가 있고, 렌즈를 통해서 들어온다. 눈의 뒤에는 망막이라고 부르는 영역이 있는데, 렌즈를 통해 들어온 빛이 망막에 맺히게 된다. 망막은 광각 세포? photosensitive cells를 가지고 있는데 여기서 빛을 감지하여, 광각 세포로 얻은 신호는 두뇌로 보내져서 우리가 보고 있는 것을 해석/보여준다.

 그런데 밝혀진 사실은 망막은 모든 부분들이 신호를 동등하개 만들어내지 않고, 특히 망막의 중간에 있는 포비아 phobia라고 부르는 영역이 망막의 다른 부분보다 가장 민감합니다.

 이 오른쪽 그래프에서 말하고자 하는것은 그래프의 y축은 시각적 활성, x축은 망막의 위치를 나타내는데, 멀리 있는 것일수록 시각 활성이 낮고, 포비아에 가까워질수록 시각활성이 증가하게 되다가, 포비아에서 가장 활성되었다가 다시 멀어지고 망막 끝에 다가가면서 내려가 시각 활성이 매우 작아지게 됩니다. 

 이것이 의미하는것은 눈에서 아주 좁은 영역에서만 고해상도로 세상을 볼수 있다는 것이고, 손을 우리 바로 앞에 놓으면 자세히 볼수 있지만 옆면으로 이동시키면, 옆에 뭔가 있다고 말할수는 있지만 정확히 그게 뭔지, 손가락이 몇 개인지 새어보기도 어렵게 됩니다. 이는 망막의 위치별로 서로 다른 민감도를 가졌기 때문입니다. 

  사람의 망막 구조로 인한 이 문제에 대처하기 위해서, 우리의 눈은 매우 빠르게 움직이고 있으며 어떤 물체를 정상적으로 보고 있는것처럼 느껴지더라도, 계속 움직이면서 여러 시각적 장면들을 가져옵니다. 이러한 눈의 매우 빠른 동작을 psychotics라고 부릅니다. 이들은 의식적으로되는 행동이 아니라 망막의 아주 일부만 민감한 문제를 극복하기 위해서 몸이 기본적으로 하는 메커니즘이 되겠습니다.

  이번에 rnn을 이용한 이미지 캡셔닝같은 경우는 사람의 빠른 눈동작의 효과가 적은 방법이지만 무언가를 볼때 그 장면의 다양한 부분들을 보게되는걸 알고 있는것 처럼, 비슷하게 어텐션을 이용한 이미지 캡셔닝 모델을 사용할때도 매 타임 스탭마다 빠르게 다양한 위치들을 훑어보게 됩니다. 이는 사람의 눈이 하는 약간의 정신적인 동작같은 거에요.

 이 아이디어가 처음으로 소개된 논문에서는 show, attend, tell이라고 부르고 있는데 이 이유는 모델은 입력 이미지를 받고, 이미지의 여러 부분들에 집중해서, 그 시점에 무엇을보았는지 단어를 생성하였기 때문입니다. 이 논문 제목이 워낙 기억하기 쉽다보니 다른 사람들도 어텐션을 다른 방향으로 사용한 모델에 대해서 이런 식으로 제목을 짓기 시작하였습니다.

 ask, attend, answer나 show, ask, attend, and answer 같은 경우에 어떤 걸 연구했는지 알수 있겠죠. 이런 모델들은 이미지를 보고, 이미지에 대한 질문이 주어질때, 이미지의 여러 부분에 집중하거나 혹은 질문의 다른 부분에 집중해서, 그 질문에 대해서 대답하는 식이겠습니다.

 "Listen, attend, and spell"의 경우 음성을 처리해서 이 소리가 어떤 단어를 발음한것인지 만들어낼것인데, 매 타임 스탭마다 단어를 만들어낼때 입력 오디오 파일의 어느 부분에 집중을 하는 식이겠습니다.

이번에는 13번째 강의를 할 차례가 되었습니다. 이번 시간에는 어텐션 Attention에 대해서 다루게 될건데 "집중하세요" pay attention 같은 엉터리 조크는 하지 않을게요. 지난 번 중간 고사 이전에 순환 신경망에 대해서 다뤘습니다.

 한번 다시 떠올려보면 순환 신경망은 다른 작업을 가능하도록 만든 다양한 벡터 시퀀스들을 처리 할수 있는 유용한 구조인걸 배웠습니다. 

 우선 순전파 신경망 feed forwad neural network에서 시작해서 순환 신경망 recurrent neural network로 고치면서 풀수 있는 다양한 문제들을 살펴보았는데, 예시로 기계 번역에 대해서 봤었습니다. 이 기계번역의 경우 한 시퀀스를 다른 시퀀스로 바꾸는 문제였어요. 다른 예시로는 이미지 캡셔닝이 있었는데, 입력 이미지가 주어질때 그에 대한 단어들의 시퀀스를 예측하는 문제였습니다.

 이번 시간에는 지난 시간 배운 순환 시긴경망에 대해서 하나하나 짚어보면서 어탠션에 대해서 다뤄보겠습니다. 

 일단 순환 신경망에서 시퀀스 투 시퀀스 문제로 돌아가서 다시 살펴봅시다. 이 과정에서는 입력 시퀀스들 그러니까 x1에서 xt까지 받는데, 이걸 가지고 y1에서 yt까지의 출력 시퀀스를 만들게 됩니다. 여기서 x들은 영어 문장의 단어 하나하나라 볼수 있겠고, y들은 스패인어 문장에서 그에 해당하는 단어들이라고 할수 있겠습니다.

 그래서 우리가 하고자 하는건 한 언어로 된 문장의 단어들을 다른 언어의 문장으로 변환을 시키는것이 되겠습니다. 다른 언어들은 서로 다른 개념들을 사용하다보니 두 시퀀스의 길이는 다를수 있습니다. 그래서 입력 시퀀스 x의 길이를 t, 출력 시퀀스 y의 길이를 t'으로 나타낼게요.

 지난 강의때 순환 신경망 아키텍처로 시퀀스 투 시퀀스 모델에 대해서 다뤄보면서 이 아키텍처는 번역 문제에서 사용할수 있다고 했었습니다. 이게 동작하는 과정을 다시 떠올려보면 인코더라고 부르는 순환 신경망이 있었는데, 인코더는 벡터 x들을 받아서 은닉 상태들의 시퀀스 h1 ~ ht를 만들어 냅니다.

 매 타임 스탭마다 순환 신경망에 대한 수식/함수 fw로 이전의 은닉 상태와 현재 입력 벡터 xi를 받아가지고 현재 은닉 상태를 만들어 냈습니다. 이 과정을 순환 신경망이 전체 입력 벡터 시퀀스에다가 적용시킬수가 있었습니다.

 여길 보면 어떻게 동작하는지 조금 더 자세한 사항내용들을 볼수 있겠는데, 입력 벡터를 처리하고 나서 전체 입력 시퀀스 내용들을 두 벡터로 정리하고자 한다고 합시다. 디코더, 출력 문장을 만들어냄,라고 부르는 다른 순환 신경망을 쓸거다보니 입력 문장을 두 백터로 정리할수 있어야 해요.

 이들 중 하나는 디코더의 초기 은닉 상태 initial hidden state로 이 그림 상에서는 s0로 표기되고 있습니다. 그리고 컨텍스트 벡터 c를 계산해야해요. 이 벡터 c는 디코더의 매 타임스탭마다 흘러/통과하겠습니다. 가장 일반적으로 구현시 컨텍스트 벡터는 최종 은닉 상태를 사용하고,  초기 은닉 상태를 가장 흔하게 선정하는 방법은 순전파 계층이나 완전연결 계층 같은 것으로 예측한 결과를 사용합니다.

-> 인코더는 디코더에서 사용할 벡터 2개를 만들어낸다. 초기 (디코더) 은닉 상태 벡터와 컨텍스트 벡터

-> 컨텍스트 벡터는 디코더의 모든 타임 스탭에서 사용되며, 인코더의 최종 은닉 상태가 주로 사용된다.

-> 초기 (디코더) 은닉 상태는 인코더의 최종 은닉 상태로부터 예측한 결과를 사용한다.

 이제 디코더를 다뤄보면 디코더가 하는일은 어느 입력 시작 토큰을 받아서 출력 시퀀스를 만들어 나가게 됩니다. 첫 타임 스탭 디코더의 출력을 구하기 위해서는 초기 은닉 상태 s0과 컨텍스트 벡터 c 그리고 시작 토큰 y0을 입력받아서 출력 문장의 첫번째 단어가 만들어 집니다.

 시간에 따라 계속 반복할건데, 디코더의 두번째 타임 스텝에서는 이전 타임 스탭의 은닉 상태 s1와 문장의 첫번째 단어 "estamos" 그리고 컨텍스트 벡터 c를 받아서 동작하고,

 여러 타임스탭을 진행하면서 입력 문장을 번역해서 "we are eating bread"가 스패인 번역기를 통해서 바뀌어지겠다. 이 구조에서 살펴봐야할 부분은 분홍색 상자의 컨텍스트 백터를 사용하고 있다는 점인데, 이 벡터는 인코딩 시퀀스와 디코딩 시퀀스 사이에서 정보를 전달하기 위한 목적으로 사용한다. 

 이 컨텍스트 벡터는 디코더가 문장을 만들어내는데 필요한 모든 정보를 요약한 것이며, 이 컨택스트 백터는 디코더의 모든 타임 스탭에서 사용된다. 이 아키텍처는 꽤 합리적이기는 하지만 문제점을 가지고 있다.

 이렇게 만든 아키텍처는 짧은 문장을 다루는 경우에 잘 동작할거고, 슬라이드의 예시와 같이 약간 긴 경우에도 잘 동작할것이다. 하지만 실제로 아주 긴 문장을 다루는 sequence to sequence 아키텍처를 사용한다고 할때, 짧은 문장을 번역하는게 아니라 책의 전체 문단을 번역하고자 하는 경우 문제가 발생할 수 있다. 

 여기서 발생하는 문제는 입력 문장, 입력 텍스트에대한 전체 정보가 하나의 컨텍스트 벡터 c로 병목화/압축해서 나타내려하기 때문인데, 벡터 하나를 가지고 짧은 문장 전체를 표현하는건 괜찬겠지만 텍스트북의 문단 전체를 하나의 컨텍스트 벡터 c로 요약하는건 어렵기 때문이다.

 이 문제를 극복하기위해서 모든 정보를 하나의 벡터 c에다가 다 집적? 요약시키기지 않는 매커니즘을 찾고자했으며, 간단한 해결책으로 하나의 컨텍스트 벡터 c로 정리하는게 아니라

 디코더의 모든 타임 스탭마다 새로운 컨텍스트 백터를 계산해 내는데, 이 새 컨텍스트 벡터는 디코더의 모든 타임 스탭에서 입력 시퀀스의 어느 부분에 집중을 할 건지 선택할수 있게 만들어 준다.

 이 좋은 방법을 정리하였고, 어텐션 attention이라 부른다.  이 슬라이드를 보면 여전히 시퀀스 투 시퀀스 순환 신경망을 사용하고 있으며, 입력 시퀀스를 인코딩해서 은닉 상태 시퀀스를 만들어내는 인코더를 가지고 있고, 매 시간마다 출력을 만들어내는 디코더를 사용할건데 차이점이라면 이 신경망에다가 어텐션 매커니즘을 추가시키겠다.

 어탠션 매커니즘은 디코더의 매 타임 스탭마다 새로운 컨텍스트 백터를 계산해내는데, 어떻게 되는지보자면 인코더는 그대로라 입력 시퀀스에 대한 은닉 상태 시퀀스들을 만들고, 디코더에서 사용할 초기 은닉 상태을 추정한다. 

 하지만 이전에 본 시퀀스 투 시퀀스 아키택처와 차이점을 볼수 있는데, 우측 상단에 배정 함수 alignment function (의미를 생각하면 위치를 배치한다?는 의미에서 배치가 맞을것같긴한데 이전에 본 배치와 햇갈리지 않게 그냥 위치를 배정한다는 의미에서 배정 함수라 하였다.)를 작성하였다. 이 배정 함수는 매개변수를 받는 완전 연결 신경망으로 작은 완전 연결 신경망이라 생각하면 되겠다.

 그래서 이 신경망은 두 벡터를 입력으로 받는데, 하나는 디코더의 현재 은닉 상태와, 다른 하나는 인코더의 은닉 상태들 중 하나를 받는다. 그러면 이 배정 함수는 디코더의 현재 은닉 상태가 주어졌을때 인코더의 각 은닉 상태들 중에서 얼마나 주의를 기울이냐, 다시말하면 디코더의 현재 은닉 상태가 인코더의 각 은닉 상태들 중에서 얼마나 가까운가 집중하는가에 대한 스코어를 출력시키게 된다.

 그래서 디코더의 매 타임스탭마다 새 컨텍스트 백터를 만들기 위해서 이 정보들을 사용할건데, 구체적으로 보자면 디코더의 맨 첫번째 타임 스탭에서 디코더 초기 은닉 상태 s0를 가지고 있겠다. 여기서 f_att 함수를 사용하여 s0와 h1이 주어질때 다른 값들이랑 비교하기위해서 일단 배정 함수 스코어로 e_11을 구하였다.

  이 배정함수 스코어는 은닉 상태 h1가 출력 은닉 상태 s0 뒤에 어떤 단어가 올지 예측하는데 얼마나 필요하는가를 나타내며, 스칼라값 e_11이 출력으로 나오게 된다. 그래서 스칼라값인 e_12는 디코더의 첫번째 은닉 상태를 가지고 단어를 예측할때 h2를 얼마나 사용되는가로 볼수 있겠다.

 그리고 이 배정 함수를 디코더의 한 은닉 상태가 주어질때 인코더의 모든 은닉상태에다가 돌려서, 인코더의 모든 은닉 상태에 대한 배정점수를 얻을수 있었다. 하지만 이 배정 스코어들은 순전파 신경망 f_att로부터 얻은것이다보니 실수값이고,

 다은 단계에서 할일은 소프트 맥스 연산을 수행해서 이 배정 점수들을 확률 분포로 만들어 주겠다. 이 솦프트맥스 함수는 이전에 이미지 분류때 봤던것과 동일한 것으로 스코어들로 이뤄진 벡터를 입력으로 받아서 확률 분포를 출력하게되는데, 가장 큰 스코어는 가장 큰 확률값이 될것이고 각 출력된 값들은 0에서 1사이의 실수 값이 되며 이들을 모두 합하면 1이 된다.

 그래서 우리는 디코더의 첫번쨰 은닉 상태에 대한 확률 분포를 예측했고, 이 확률 분포는 인코더의 각 은닉 상태들 중에서 얼마나 가중을 줄지를 알려주다보니 이들을 어탠션 가중치 attention weights라고 부른다. 

 다음에 할일은 얼핏보면 어려워보이지만, 은닉 상태 각각에대한 가중합을 가져와서 사용하겠다. 이들을 예측된 확률 스코어 만큼 가중을 줘서 더하여, 디코더의 첫번째 타임스탭에서 사용할 컨텍스트벡터 c1을 만든다.

 이게 의미하는건 입력 시퀀스에대한 (인코더의)각 은닉 상태들을 얼마나 가중치를줘서 반영시킬지를 예측해서 디코더의 모든 타임스탭마다 동적으로 가중치를 변화시키면서 디코더의 매 타임 스탭마다 다른 컨텍스트 백터를 구할수가 있겠다.

 그러면 이제 디코더의 첫 타임 스탭을 동작시킬수가 있겠고, 이 디코더 신경망은 방금 막 계산한 컨텍스트 벡터와 (이 슬라이드에는 빠트렸지만) <start> 토큰을 입력으로 받아서 문장에서 첫번째 예측되는 단어를 출력한다. 

  정리를하자면 문장의 각 단어들을 생성시키고자 할때, 출력 문장의 각 단어는 입력 문장의 하나 혹은 여러개의 단어에 대응된다. 그래서 디코더 신경망이 입력의 한 부분에 집중할수 있도록 해주는 컨텍스트 백터를 매 타임 스탭마다 동적으로 만들어낸게 되겠다.

 그래서 여기서 보는 예시는 "we are eating bread"라고 하는 특정한 문장을 번역하는것으로 첫번째 단어 "estamos"는 스페인어로 "we are doing somthing"이란 뜻을 가지고 있다. 영어문장에서 첫, 두 단어에 가중을 두고 나머지 두 단어에는 가중치를 적게 준다면, 디코더 신경망이 단어들을 만드는데 입력 시퀀스에서 중요한 부분에 집중할수 있게 된다.

 다른 중요한 점으로 이 모든 연산들은 미분 가능한것들이며, 우리가 신경망한태 디코더의 매 타임스탭마다 어디에 집중하라고 알려주기보다는 신경망이 스스로 어디를 집중해서 보도록 만들었다.

 지금 보고 있는 계산 그래프의 모든 연산들은 미분가능하다보니 우리가 따로 지시하거나 신경망에게 어딜 보라고 할 필요없이, 이런 큰 연산을 하나의 계산그래프를 만들고 신경망의 모든 파츠들을 역전파를 통해서 최적화 시키면 되겠다.

 다음 타임 스탭에서 이 과정을 반복해서, 디코더의 새 은닉상태 s1을 가져와서 이 은닉상태와 입력 시퀀스의 각 은닉 상태를 비교해서 새로운 배정 스코어 e21, e22, ... 등 시퀀스를 만들어낸다.

 그리고 소프트맥스를 적용해서 입력 시퀀스에 대한 확률 분포들을 구해내고, 이 확률 분포는 출력 시퀀스에서 두 번째 단어를 만들어낼때 입력 시퀀스의 어떤 단어에 집중을 할것인가를 알려주며, 이 추정 확률로 입력 시퀀스의 은닉 상태에대해 가중 합으로 새 컨텍스트백터를 만들어내겠다.

 이전의 과정을 다시 반복해서, 두번쨰 컨택스트 벡터와 첫 번째 단어, 이전 은닉 상태로 두 두번째 은닉 상태를 계산한뒤 두번쨰 단어를 생성해내겠다.

 정리하자면 무언가를 먹다는 걸 의미하는 두번째 단어 "comiendo"가 생성된 것은 모델이 "eating"의 타임 스탭에 가중치를더 줘서 집중했으며, "we"나 "bread"같은 단어는 생성시키는게 적정하지 않은것으로 보고 무시했다고 할수 있겠습니다.

 다시말하지만 이 모델은 미분가능해서 학습시킨것으로 우리가 모델에거 어떤 단어, 부분이 집중하라고 알려줬기보다는 모델이 출력 시퀀스를 생성할때 어떤 부분을 집중할지 학습한 것입니다.

 그래서 이제 여러 타임 스탭으로 풀어나가서 이와 같이 어탠션으로 학습한 시퀀스 투 시퀀스 예시를 볼수 있겠습니다. 이 방법을 통해서 바닐라 시퀀스 투 시퀀스 모델이 가지고 있던 문제를 극복할수가 있었습니다.

 왜냐면 이건 입력 시퀀스에 대한 전체 정보를 하나의 단일 벡터에 넣어서, 그 한 벡터를가지고 디코더의 모든 타임스탭에다가 반영시킨것이아니라 디코더에게 각 타임스탭마다 새로운 컨텍스트백터를 생성해서 줬거든요. 그래서 다시 정리하자면 우리가 아주 엄청 엄청 긴 시퀀스를 다루더라도 모델이 디코더의 각 출력때마다 입력 시퀀스에서 주의를 집중할 부분을 이동/바꿀수있게 되었습니다.

 우리가 지금까지 기본적으로한것은 순환 신경망 모델인 시퀀스 투 시퀀스를 학습시켰고, 이 모델은 영어로된 단어들의 시퀀스를 입력받아 프랑스어 단어 시퀀스를 출력시킨다고 합시다. 그림에서 뒤집혓을수도 있긴한대 햇갈리니 넘어가겠습니다.

 하지만 결국에 하는 일은 영어 단어들과 프랑스 단어들/문장을 번역하는 작업을 할 것인데, 이 어텐션을 이용한 시퀀스 투 시퀀스 모델을 학습시킨것이고, 디코더의 타임 스탭마다 출력 시퀀스를 만드는 과정에서 입력 시퀀스의 어떤 단어에 주의를 기울일것인지를 정리하는 입력 시퀀스의 모든 단어들의 확률 백터를 만들어 냅니다. 

 그래서 우린 여기서 어탠션 가중치를 이 모델이 번역 작업을 할 때 어떤 결정을 내렸는가, 어떻게 결정을 내렸는가로 이해/해석 할 수가 있어요. 

 위 슬라이드를 보면 위에 영어 문장으로 "the agreement on the european economic area was signed in august 1992"가 있고, 그 아래에 프랑스어로 동일한 의미를 나타내는 문장이 있어요.

 여기서 재미있는 부분은 이 다이어그램은 출력의 모든 타임스탭에서 어탠션 가중치가 어떤지를, 즉 모델이 어떤 선택을 했는지를 보여주고 있어요. 그래서 이 그림으로 해석할수 있는 구조 부분들이 많은데, 첫번째로 볼수 있는 건 왼쪽 위 코너에서 어텐션 가중치의 대각 패턴을 볼수가 있어요. 이 패턴의 의미는 "the"라는 단어가 프랑스어 토큰 L'를 생성하는대서 가장 집중을 했다는 의미입니다.

  그 다음 영단어 "agreement"는 프랑스 단어 "accord"를 만들때 가장 집중되었다는 것이고, 그래서 출력 시퀀스의 처음에서 네 번째 단어를 생성하는데까지 일대일 대응되었다고 이해/해석할수 있겠습니다. 그리고 이 대응관계는 모델이 스스로 찾아내는것이지 우리가 모델에게 문장의 어떤 부분이 배정/매칭되는지 알려준게 아니에요.

  하지만 여기서 가장 놀라운 부분은 프랑스어로 "zone economique europeenne", 영어로는 "european economic area"인데, 여기서 세 단어는 같은 의미이지만 다른 순서로 되어있어요. 프랑스어 "zone"은 영어로 "area"이고, 영어로 "economic"은 프랑스어로 "economique", "european"은 "europeenne"와 대응되는 구조인것을 볼수 있고, 이 모델은 이 세 단어의 순서를 뒤집어서 대응시키고 있어요.

  이 어텐션 매커니즘에서 좋은 점은 다른 신경망 아키텍처와는 달리 이 모델이 어떻게 결정을 내렸는지에 무엇을 골랏고 무엇을 안 골랐는지에 대해서 어느정도 해석할수있는 점이되겠습니다.

 그래서 이 어텐션 매커니즘으로 시퀀스를 생성했고, 단어 생성시 매 타임스탭마다 입력 시퀀스의 서로 다른 부분들을 집중해서 보았습니다. 하지만 이 어텐션 메카니즘의 수학적인 구조에 대해서 알아차릴수 있는점은 입력이 시퀀스라는 사실을 신경쓰지 만들었다는 점입니다.

 이러한 기계 번역의 작업에서 입력을 시퀀스로 받고 출력도 시퀀스가 되었지만, 어탠션 매커니즘의 목표는 시퀀스인 입력 벡터들을 사용하는것이 아니라, 시퀀스가 아니더라도 다른 종류의 데이터에도 집중할수 있도록 어텐션 메카니즘이 만들어졌어요.

**다음에는 이미지 캡셔닝과 어탠션에 대하여...

 지금까지 기본 바닐라 RNN의 그라디언트 플로우를 보면서 그라디언트 폭증, 소멸 문제에 대해 살펴봤다. 그라디언트 소멸 문제를 고치기 위해서 사람들은 이 Vanilla RNN대신 다른 아키텍처를 사용하기 시작하였으며

LSTM Long Short Term Memory 장단기 메모리라고 부르는 방법을 주로 사용하고 있다. 한번 보면 다소 복잡해보이고, 햇갈리게 생겼다보니 이 식을 보면 어떻게 돌아가고 이걸로 어떻게 문제들을 푸는지 명확하게 이해하기는 어렵겠다.

 LSTM은 기본적으로 하나의 은닉 유닛 벡터만을 사용하는게 아니라 두 은닉 벡터를 사용하는데, 하나는 셀 상태 cell state라고 부르는 c_t와 은닉 상태 hiddent state h_t가 있겠다.

 이전 은닉 상태와 현재 입력을 가지고 서로 다른 4개의 게이트 값 i, f, o, g를 계산을 하고, 이 들을 이용해서 갱신된(현재의) 셀 상태와 은닉 상태를 구한다. 여기서 짚고 넘어가고 싶은건 LSTM은 1997년에 나왔다는 점인데, 10년간 잘 알려지지는 않았지만 2013, 2014년경 사람들이 LSTM 아키텍처를 사용하기 시작하면서 점점 대중화되기 시작했고, LSTM 아키텍처가 현재 시퀀스처리에 가장 널리 사용되는 순환 신경망 아키텍처가 되었다.

 LSTM에 대해서 조금 더 풀어서 매 타임스탭마다 어떻게 동작되는지를 살펴본다면, 입력 x_t와 이전 은닉상태인 h_t-1을 받겠다. 그리고 순환 신경망 처럼 입력 벡터 x_t와 이전 은닉 상태 h_t-1를 연결 concat시키고, 어떠한 가중치 행렬을 곱한다.

 바닐라 순환 신경망 Elman RNN에서 이 행렬곱 연산의 결과에다가 tanh 비선형 함수를 적용해서 현재 은닉 상태값을 계산하였었지만

  LSTM에서는 각각 크기가 H(H는 은닉층 유닛 개수)인 4개의 서로 다른 벡터를 출력할수 있도록, 행렬곱 연산을 다듬어서 출력을 계산하며 이 출력들을 게이트라고 부른다. 입력 게이트 input gate, 망각 게이트 forget gate, 출력 게이트 output gate, 더 나은 표현이 떠오른는게 없어서 게이트 게이트 gate gate로 4가지가 있다. 

 이 슬라이드에 행렬곱으로 출력(은닉 상태에 tanh 적용한것)을 바로 예측하기보다는 4개의 게이트를 예측한 다음에 이 4가지 게이트로 현재(갱신된) 셀 상태와 은닉 상태를 구한다. 

 여기서 주의해야할 점은 이 4개의 게이트들은 서로 다른 비선형 함수가 적용되는데, 입력 게이트, 망각 게이트, 출력 게이트는 전부 시그모이드 비선형 함수를 적용시키며, 그러면 0과 1사이 값을 가지게 되겠다. 게이트 게이트의 경우 tanh 함수를 통과 시키며 그러면 -1 에서 1 사이 값을 가지게 되겠다.

 그 다음에 c_t에 대한 식을 보면 이전 셀 상태인 c_t-1과 망각 게이트를 원소 단위 곱샘을 하는데, 망각 게이트가 0 ~ 1사이 값을 가지고 있다보니, 망각 게이트는 셀 상태의 원소들을 0으로 리셋을 시키거나 셀 상태를 순방향으로 계속 전파를 시키는것으로 이해할수 있으며 이게 망각 게이트가 하는 일이 되겠다.

  그리고 c_t에는 입력 게이트와 게이트 게이트의 원소 단위 곱을 더하고 있는데, 게이트 게이트는 -1 ~ 1 사이 값을 가지는 것으로 셀 상태에 쓰고자 하는 값(반영 하고자 하는 값)을 나타낸다. 입력 게이트는 0과 1사이 값을 가지는데 시그모이드 함수를 적용했기 때문이며, 게이트 게이트와 원소단위 곱샘을 함으로서 정리하자면 게이트 게이트는 1을 더하거나 -1을 빼는 역활을 하고, 입력 게이트는 그 셀의 모든 지점에서 실제로 값들 더할지 뺄지 판단하는 역활을 한다.

 이제 최종 출력 상태를 계산하기 위해서는 셀 상태를 tanh 비선형 함수에 적용시키고, 출력 게이트와 원소 단위 곱샘을 하면 되며, 이 과정이 lstm이 lstm은 셀 상태의 일부를 출력 게이트로 조작하여 매 타임스탭마다 드러낼지 말지 를 선택할수 있다. 그래서 출력 게이트는 셀 요소들을 얼마나 밖으로 내보낼지 혹은 은닉 상태로 감출치

 최종 출력 상태는 셀 상태를 tanh 비선형 함수에 적용 시키고나서 출력 게이트와 원소 단위 곱샘을 통해서 계산하며, 이 과정을 정리하자면 셀 상태는 lstm에서 처리되는 내부 은닉 상태로서 lstm은 매 타임 스탭마다 어떤 셀 상태를 밖으로 드러낼지 출력 게이트로 정할수 있겠다.

 그래서 출력게이트가 ㅎ하는 일은 얼마나 많은 셀들을 드러내거나 은닉 상태로 나둘지를 정한다고 할수있겠다. 출력 게이트의 일부 원소들을 0으로 지정한다면 셀 상태의 원소들은 밖으로 나오지 못한채 은닉 될 것이고, 내부적인 변수로서 lstm에 유지되겠다. 

 LSTM을 설명하기위한 복잡한 그림들이 많긴한데, 이 걸 보면서 단일 LSTM의 처리 과정을 이해할수 있겠다. 이 그림을 보면 왼쪽에서 이전 셀 상태 c_t-1과 이전 은닉상태 h_t-1을 받고, 이전 은닉 상태와 현재 입력 x_t를 쌓은 다음에 가중치 행렬과 곱하고 있다.

 그 결과 4개의 게이트로 나누어져 이 게이트들은 셀 상태 c_t와 은닉 상태 h_t를 계산하는데 사용 되겠다. LSTM을 이 방식으로 살펴보면서 흥미로운 점은 바닐라 RNN과 비교했을때, 그라디언트 플로우에 대해서 다른 관점으로 볼수 있겠다.

 한번 현재 셀 상태 c_t로부터 이전 셀 상태 c_t-1로 역전파를 한다고 생각해보자. 그러면 위와 같이 꽤 깔끔하게 그라디언트 경로가 만들어진다. 왜냐면 역전파를 할때 덧셈 노드를 만나는 경우, 역전파에서 덧샘 노드는 그라디언트를 복사 하는 역활을 했지, 정보를 죽이지는 않았었다. 그래서 처음 덧샘 노드를 만났을때, 들어온 그라디언트는 LSTM 내부로 퍼지게 되겠다.

 그 다음에 망각 게이트와 원소 단위 곱샘을 역전파하는 경우, 여기서 정보가 제거될 위험이 있다. 그 이유는 시그모이드 비선형 함수를 역전파 과정에서 통과하기 때문이 아니라, 비선형 함수 , 원소 단위로 0과 1사이의 상수값을 곱한것을 역전파하다보니 정보가 사라질 위험을 가지기 때문이다.

 망각 게이트가 0에 가깝다면 정보가 사라질 위험이 있으나, 1에 가깝다면 현재 셀 상태에서 이전 셀 상태로 역전파시에 정보들이 사라질 위험은 없겠다. 그렇다보니 어떤 비선형 함수도 지나가지도 않고 행렬 곱 연산도 역전파 과정에서 지나가지 않다보니 LSTM의 탑 레벨 경로가 간단하게 흘러가는걸 볼수 있겠다.

-> 이 부분 내용을 정리하면

일단 LSTM의 탑래밸에서는 셀 상태 역전파를 보면,  sum 노드에서의 역전파는 분배되다보니 그대로 지나가고,

(시그모이드 함수 역전파 때문이 아니라) 원소 단위 곱샘 노드 때문에 정보가 사라질수도 있는데, 

 망각 게이트는 0과 1사이값을 가지고 있으며, 0에 가까우면 순전파시 정보가 사라지지만 1에 가까울때 역전파시에는 정보가 사라지지 않는다

 그래서 덧샘 노드와 원소 단위 곱샘 노드를 깔끔하게 지나가는 그라디언트 경로가 만들어지는것 같다.

 여러개의 LSTM 셀들을 연결 시켰을때 시퀀스를 처리하고 나서 맨 위의 셀 상태들이 지나가는 통로를 보면 인터럽트 받지 않은 고속도로같이 되는걸 볼수 있다. 이 통로를 통해서 시간에 따라서 역방향으로 정보가 쉽게 통과할 수 있겠다.

 LSTM 모델은 바닐라 RNN과 비교해보면 역전파 진행시 그라디언트 플로우가 더 잘 흘러갈거라고 볼수 있겠다 하지만 여전히 가중치 때문에 문제가 발생할수 있겠는데, 바닐라 RNN의 경우 그라디언트는 시간에 영향을 받아, 아주 긴 타임 스탭을 거친다면 정보들이 훼손되어 제대로 학습을 할수가 없다.

 하지만 LSTM에서는 역전파 과정에서도 정보들이 보존되어 흘러갈수 있는 통로가 있다보니, 가중치로 역전파 후에 행렬곱이나 비선형 연산을 지나가더라도 고칠수가 있겠다.

 하지만 행렬곱이나 비선형 함수를 지나가면서 역전파를 시킬 필요가 없는 경로가 있었는데, 학습 과정에서 정보가 계속 흘러가도록 하기 위해서 여전히 h_t를 가지고 있도록 하였다.

 그래서 LSTM의 셀 상태는 LSTM의 프라이빗 변수라고 보면되고, 은닉상태 h_t는 LSTM의 출력을 내기 위해서/예측하기 위해서 사용한다. 

 LSTM을 보면 인터럽트 되지 않는 그라디언트 고속도로를 가지도록 설계되었는데, 이와 비슷한 아키텍처를 이전에 한번 본적이 있었습니다. ResNet으로 아주 심층 합성곱 신경망을 학습하는 문제를 해결하기 위해서 스킵 커낵션을 추가시켰고, 그 결과 그라디언트가 아주 많은 계층에서 잘 퍼져나갔습니다. LSTM에도 동일한 아이티어라고 보면 될거같습니다.

LSTM과 ResNet은 많은 부분에서 공통점을 가지고 있는다고 볼수 있겠고,  재미있는 신경망으로 고속도로 신경망이 있다. 이 신경망은 ResNet 이전에 나오기는 했지만 LSTM을 닮았으며 한번 확인해보면 좋겠다.

 지금까지 단일 계층 RNN에 대해서 살펴보면서, 입력 시퀀스를 간편하게 처리해서 은닉 층 시퀀스를 만들고, 이 은닉 벡터들의 시퀀스로 출력 시퀀스를 만들어냈다. 지금까지 이미지 처리를 하는 경우를 봤는데 더 많은 계층을 사용하면 모델 성능을 개선 시킬수가 있겠는데 순환 신경망의 경우에도 그렇다.

  다층을 쌓는 방법은 기존의 순환 신경망의 은닉 상태를 또다른 순환 신경망에다가 입력으로 넣으면 된다. 이렇게 만든 걸 다층 혹은 심층 순환신경망이라 부를수 있겠다. 과정은 첫 입력 시퀀스를 처리해서 은닉 상태 시퀀스를 만들고, 그 은닉 상태 시퀀스를 다음 순환 신경망의 입력 시퀀스로 사용해서, 두번째 은닉 상태 시퀀스를 만들어 낸다.

 더 깊이 쌓고자 하는 경우 GPU 메모리가 되는 만큼 더 쌓으면 되겠다. 이런 순환 신경망을 여러 층으로 계속 쌓아서 사용해도 되겠지만, 순환 신경망을 실제로 쓴다면 3 ~ 5계층이면 충분하며, 합성곱 신경망 처럼 아주 깊은 모델은 잘 사용되지는 않는다.

(질문) 다른 순환 신경망 계층 마다 서로 다른 가중치 행렬을 사용하는가?

O. 다른 계층끼리 다른 가중치 행렬을 사용한다.

 다루고 싶은 수많은 문제들이 있고, 현재 신경망을 고쳐서 더 나은 수식을 정리해서 문제를 해결할수 있으면 좋겠지만 수많은 다른 순환 신경망 아키텍처를 이용한 논문들이 나오고 있다.

 여기서 중요한 방법중 하나로 위 슬라이드 왼편에 있는 gated reccurent unit GRU라고 부르는 방법인데, LSTM의 간편화 시킨 버전이라고 볼수 있겠다. 이 방법에 대해서 깊게 설명하지는 않겠지만 그라디언트 흐름을 개선시키기 위해서 가산 연결을 사용하였다.

 그리고 컴퓨터 계산 비용이 점점 저렴해지기 시작하면서 사람들이 부르트 포스 방법을 싸용하기를 시작했는데, 최근 몇년전에 혁신적인 탐색방법을 사용하였는데, 부루트 포스 방법으로 수만개의 수식 공간들을 탐색해서 서로 다른 순환 신경망 모델을 만들어서 찾아보았다.

 이 논문에서 찾은 갱신 공신 3가지를 볼수 있는데, LSTM보다 더 잘 동작한다고 볼수있을만한 건 없었다. 비슷한 성능을 보이는 수많은 수식들이 존재하지만 LSTM은 사람들이 가장 처음 발견한 것이고, 사람들이 지금까지 사용하는 역사적으로 좋은 모델이라 할수 있겠다.

 이미 몇 강전에 신경망 아키텍처 탐색 방법에 대해서 살펴보았는데, 합성곱 분야에서 다른 신경망 아키텍처를 생성하는 신경망, 간단하게 소개만 하고 자세히 다뤄보지는 않았다. 사람들은 순환 신경망 아키텍처에도 이와 같은 방식을 적용해서 찾아보았다.

(내용 조금 남았는데 힘드니까 마무리)

 순환 신경망을 컴퓨터 비전 분야에 활용한 예시로 이미지 캡셔닝이 있겠다. 이 이미지 캡셔닝은 이미지 하나를 입력으로해서 문장을 출력시키는 일대다문제라고 할수 있는데,

 이미지를 합성곱 신경망에다가 입력으로주어 특징들을 추출시키겠다. 그렇게 추출한 특징들을 순환 신경망 언어 모델에 대입하여 문장을 만들수 있도록, 이미지 데이터셋과 이미지에 대한 캡션들을 사용해서 이 언어 모델을 경사 하강법으로 학습 시키겠다.

 이 그림은 이게 어떻게 생겻는지 보기위한 전이 학습의 구체적인 예시라고 할수 있는데, 우선 이미지넷으로 선학습시킨 CNN모델을 다운받아서 가져오고, 그 신경망 모델의 마지막 2계층을 제거시키겠다. 

 이제 유한한 임의 길이의 시퀀스를 절단 시간 역전파를 사용해서 처리한다고 해보자. 이미지 캡셔닝에서는 <start>와 <end>로 이뤄진 시퀀스를 가지고 처리하는데 항상 시퀀스의 첫번째 요소, 시작 요소는 <START>로 새로운 문장의 시작점을 의미한다.

 이제 합성곱 신경망으로부터 얻은 데이터를 순환 신경망에서 사용해보자. 지난번에 이전 상태의 은닉 상태를 이용해서 현재 은닉 상태를 계산하는 공식을 약간 변환을 시켰는데, 이미지 정보를 반영해서 매 시점마다 세 입력을 받게 되었다.

 시퀀스의 현재 요소와 이전 은닉 상태 그리고 선학습 합성곱 모델에서 얻어낸 특징까지 이 세가지 입력을 서로 다른 가중치 행렬 혹은 선형 사영을 한뒤 이들 모두를 합한 휘 tanh 함수를 적용시키는 형태로 기존의 순환 신경망 순환 함수를 변경시켰다. 이와 같이 변경 시킴으로서 이미지에 대한 특징 백터 정보를 추가적으로 반영할 수 있었고, 

 이 이후에는 언어 모델처럼 동작하게 되겠다.

 훈련을 마치고나서 테스트 때 어떻게 동작하는지를 보면, 우선 첫번째 단어를 얻고자 사전에 있는 단어, 토큰에 대한 확률 분포를 예측하여 "man"이라는 단어를 얻을수가 있겠다. 

 이 단어 "man"을 순환 신경망의 다음 입력으로 사용해서 다음 단어인 in을 얻고

이 과정을 반복해나가면, "straw", "hat" 등 단어들을 얻을수가 있겠다.

 그리고 마지막에는 <END> 토큰이 나오면서 멈추게 되겠다. 이 처럼 유한한 길이의 시퀀스를 처리하는경우 사전에 <START> 토큰을 시퀀스의 맨 앞에, <END> 토큰을 시퀀스의 맨 뒤에 추가시켜서 학습하는 과정에 사용하며, 테스트 시점에서 <END> 토큰을 구하는 순간 출력을 멈출 시점으로 판단하여 샘플링/예측 과정을 종료하게 된다. 

(질문) 위 수식에서 파랑 항과 분홍 항의 차이는 무엇인가

 위 변경된 함수를 보면 녹색, 파랑, 분홍 세 가지 항이 있는데, 녹색항은 현재 시점 시퀀스 입력으로 입력 토큰 값중 하나를 나타내며 이 예시에서는 <START>, man, in, straw, hat 중 하나가 사용되겠다. 파랑 항의 h는 이전 시점의 은닉 상태를 나타내며 예를들어 h2를 계산하는 경우 h1을 의마한다고 할수 있겠다. 이번에 분홍 항의 경우 합성곱 신경망으로부터 얻은 특징 벡터 v를 나타내는데, 순환 신경망의 모든 시점에서 사용되겠다.

 이미지 데이터셋과 그에 대한 캡션들을 가지고 이미지 캡셔닝 모델을 학습시키켰을때 이미지를 아주 잘 설명하는 경우드를 한번 보자. 맨 왼쪽 위의 것을 보면, "고양이가 가방 안에 앉아있다."라는 결과가 나왔는데, 이전에 살펴보았던 단일 라벨만 출력시켰던 이미지 분류 모델보다 훨씬 자세하게 설명할수 있다.

 다음으로 위의 맨 오른쪽을 보면 "하얀 곰인형이 잔디밭 위에 앉아있다."라면서 좋은 결과를 얻었고, 아래를 보면 "두 사람이 서핑 보드를 들고 해변가를 걷고 있다", "테니스 선수가 동작을 하고 있다"와 같이 이미지들을 상당히 잘 설명하고 있는걸 볼수 있겠다. 

 그래서 이미지 캡셔닝에 대한 첫 연구 결과가 나오면서 그동안 "고양이", "개", "트럭" 같은 단순한 단일 라벨이 아니라 주어진 이미지를 보고 의미있는 출력을 내면서 많은 사람들이 열광하곤 했었다.

 하지만 얼마 안가서 이런 이미지 캡셔닝 모델이 생각 많큼 똑똑하지 못하다는게 드러났는데, 한번 실패한 경우들을 살펴보자. 

  왼쪽 위 이미지를 훈련된 이미지 캡션 모델에다가 주면, "한 여성이 고양이를 손에 쥐고있다"라는 결과가 나오고 있다. 아마 여성의 옷의 텍스처/질감이 훈련셋에 있는 고양이 털과 비슷해서 일수도 있겠다.

 그 아래 이미지를 보면 "한 사람이 책상 위에서 컴퓨터 마우스를 쥐고 있다."라는 결과가 나온 경우인데 여기서 사용한 데이터셋이 아이폰이 나오기 전에 만들어지다보니, 여기 나오는 사람이 책상에서 뭘 쥐고 있던간에 컴퓨터 마우스나 다른 휴대폰으로 판단하게 되겠다.

 이와 같이 이미지 캡셔닝 모델은 꽤 재미있을지는 몰라도 여전히 부족한 점이 많으며, 이런 문제들을 해결하려면 꽤 걸릴것으로 보인다.

 다음으로 살펴봐야할것으로 순환 신경망의 그라디언트 플로우/흐름이 있겠다. 위를 보면 우리가 지금까지 다뤄온 바닐라 순환 신경망에 대한 그림이 있는데, 여기서 순환 신경망이 한 타임 스탭에서 어떻게 처리되는지를 보여주고 있다.

 입력 x_t가 아래에서 들어오고, 왼쪽에서 이전 은닉상태 h_t-1이 들어온다. 이 두게를 연결시키고나서 가중치 행렬 W에 대한 선형 변환으로 정리 할수 있고, 여기다가 tanh 비선형 함수를 적용시켜서 현재 상태 h_t를 구할수가 있겠다.

 여기서 우리가 알아야 하는 부분은 이 모델이 역전파 하는 과정에서 그라디언트가 어떻게 되는가인데

 한번 역전파가 진행되는 과정에서 어떤일들이 생기는지 한번 생각해보면, 일단 출력 은닉 상태 h_t에 대한 비용함수의 미분치를 받을게 되겠다. 우리가 구하고자하는건 입력 은닉 상태 h_t-1에 대한 비용의 그라디언트를 계산해야 한다.

 여기서 두가지 문제가 생기는데, 그 중 하나는 tanh 비선형 함수를 사용하는것으로 여러번 왜 tanh 함수가 안좋은지 이야기 했고 가능한 쓰지말아야하며, 문제가 생길 가능성이 있다고 보아야한다. 하지만 이 rnn모델이 90년대에 만들어진것이다보니 감안해야 되겠다.

 이 순환 신경망 모델에서 역전파를 할때 생기는 또 다른 큰 문제로는 역전파시 행렬곱 부분인데, 역전파 과정에서 가중치 행렬의 전치 행렬을 곱해야 한다.

 그러면 한번 단일 순환 신경망 셀이 아니라 여러 타임 스탭을 흘러간 순환 신경망을 다뤄보자. 그러면 여기서 전체 시퀀스를 역으로 흘러가는 그라디언트 플로우를 볼수 있겠다. 업스트림 그라디언트는 계속 계속 동일한 가중치 행렬의 전치행렬과 곱해나가게 된다.(순환 신경망에서는 하나의 가중치 행렬을 공유= 모든 시점의 가중치 행렬이 동일하므로) 

 이렇게 되면 아주 안좋은 결과를 얻을수 밖에 없는데, 이 슬라이드에서는 4개의 셀만 보여주고 있지만 100 혹은 200 혹은 수천 타임 스탭의 시퀀스를 풀어나가는 경우에 역전파 과정에서 동일한 가중치 행렬을 수천번 곱해나가면 두 가지 방향으로 잘못 동작하게 된다.

  발생되는 문제들 중 하나는 행렬이 아주 크다면, 같은 행렬을 계속 곱하다보면 점점 커져 무한대로 커지게 될것이고, 가중치 행렬의 가장큰 특이 값이 1보다 작다면, 그라디언트는 급격히 줄어들어 0이되어 사라져버리게 되겠다.

 다시 정리하면 가장큰 특이값이 1보다 크다면, 그라디언트가 무한대로 폭증할것이고, 가장 큰 특이값이 1보다 작다면 그라디언트가 0이 되어버리겠다. 그래서 이와 같은 그라디언트 폭증, 그라디언트 소멸 문제를 가지게 되므로, 아주아주 긴 시퀀스를 처리할때 안정적으로 학습시키기 위해서는 가중치 행렬의 모든 특이값이 정확히 1이 되도록 만들면 되겠다.

 그래서 사람들이 그라디언트 폭증을 대처하기 위해서 사용하는 방법은 그라디언트 클리핑/다듬기?이라고 부르는 방법을 사용하는데, 역전파에서 실제 그라디언트를 사용하는것이아니라, 은닉 상태에 대한 그라디언트를 계산한 후에, 그라디언트의 유클리디안 노름이 너무 큰지 체크를해서 그렇다면, 그라디언트가 줄어들도록 위의 값을 곱해주는 방법이 되겠다.

 그래서 이 그라디언트 클리핑을 사용한 덕분에 실제 그라디언트를 계산한것은 아니지만 적어도 그라디언트가 폭증하는건 막아 역전파를 계속할수 있게 되겠다. 하지만 이 방법은 실제 그라디언트를 계산해서 쓰는게 아니다보니 좋은 방법이라 할수 없고, 그저 그라디언트 폭증을 방지하기 위해서 사용했던 경험적인 방법이었습니다.

 그리고 다뤄야 하는 또 다른 문제로는 그라디언트 소멸 문제로, 특이 값이 아주아주 작은 경우에 발생하는 이 문제를 피하기 위해서 사람들이 이 기본 아키텍처 대신 다른 순환 신경망 모델을 사용하였습니다.