
그래서 순환 신경망 recurrent neural network란 무엇이고, 어떻게 해야 그게 잘 동작할까. 기본적으로 순환 신경망은 순차적으로 처리한다고 말했었는데, 매 타임 스탭마다 순환 신경망은 위의 빨간색 상자 x와 같이 어떤 입력을 받고 파란색 상자에 나와있는 출력 y를 내보낸다.
거기다가 순현 신경망은 내부 은닉 상태 internal hidden state라고 하는 벡터를 가지고 있는데, 매 타임스텝마다 순환 신경망은 현재 타임 스탭의 입력을 어떤 공식에 따라 은닉 상태를 갱신시키는데 사용한다. 그러면 갱신된 은닉 상태는 현재 타임 스탭에대한 출력으로 내보내진다.
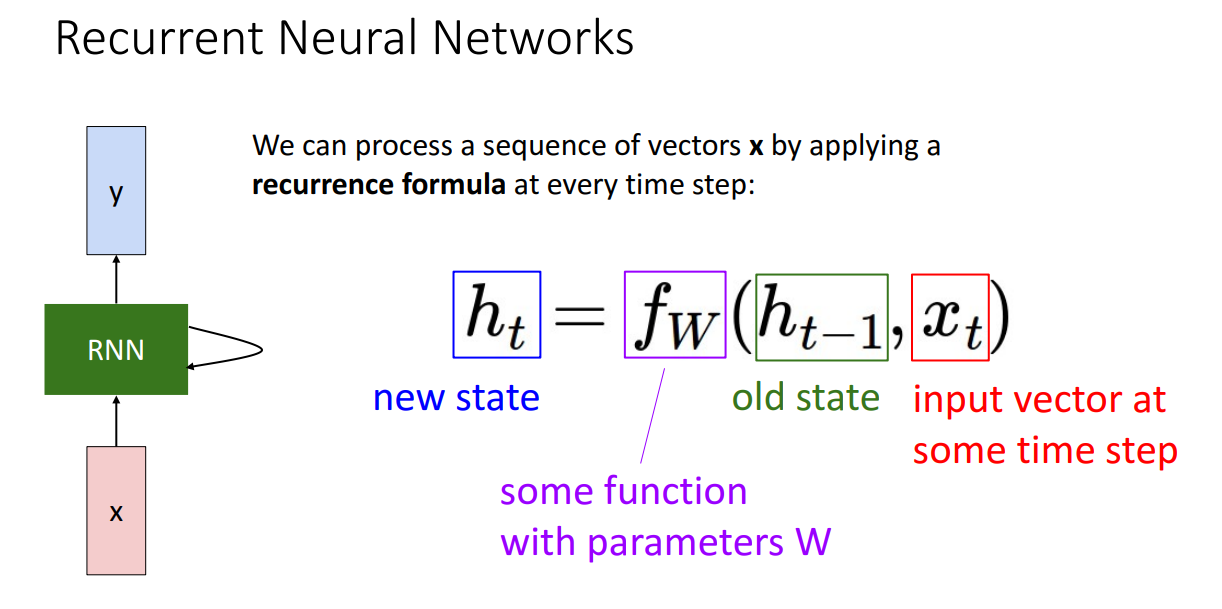
이게 어떻게 되는지 구체적으로 보자면, 순환 신경망 아키텍처를 정의하기 위해서 우선 순환에 대한 함수 $f_w$를 정의하여야 한다. 위 그림을 보면 $h_t$가 있고, 이 신경망은 은닉 상태에 대한 시퀀스를 처리하는걸 알수 있는데 여기서 $h_t$는 현재 타임스탭에서의 은닉 상태로 벡터 형태로 되어있으며 우리가 그동안 봐왔던 완전 연결 신경망의 은닉 층 활성 벡터 같은것이라고 보면 되겠다.
이제 순환 관계에 대한 함수 f를 정리하자면 f는 학습 파라미터 w의 영향을 받는 함수로 입력으로 이전 타임 스탭 $h_{t-1}$과 현재 타임 스탭에서의 입력 $x_{t}$를 입력으로 받아서 계산된 은닉 상태 $h_t$를 출력하게 된다.
$f_{W}$는 입력 벡터와 은닉 상대의 관계에 따라 대수적 방정식을 정의해서 사용하면 되겠다.

여기서 중요한건 매시간 스탭마다 시퀀스에대해서 동일한 가중치 W와 동일한 함수 $f_{W}$를 사용하는 것이며, 이렇게 함으로서 가중치를 공유하고 모든 각 시간에서 같은 가중치 행렬을 사용해서 처리할수 있겠다. 그래서 이 함수는 모두 같은 가중치 행렬로 매 시간마다 시퀀스를 처리하다보니 임의 길이의 시퀀스를 처리할수 있는 하나의 가중치 행렬을 가진다고 할수 있다.

이제 순환 신경망에 대한 일반적인 정의 형태를 가지고 첫번째로 구체적인 예시를 구현하여보자. 위 그림은 가장 간단한 순환신경망 버전으로 바닐라 순환 신경망 혹은 그냥 순환 신경망, 연구자의 이름을 따 Elman RNN이라고도 부른다.
여기서 은닉 상태는 하나의 벡터 $h_{t}$이며, 가중치 행렬들을 이용하여 학습하는데 가중치 행렬 중 하나인 $W_{hh}$는 이전 타임스탭의 은닉층과 곱하고, 다른 하나인 $W_{xh}$는 현재 타임 스탭의 입력과 곱한다. 여기서 현재 입력 $x_{t}$와 가중치 행렬 $W_{xh}$를 곱한 것과 $h_{t-1}$과 $W_{hh}$을 더하면 되는데 여기에 편의를 위해서 생략했지만 편향항 혹은 정규 편향항을 명확하게 정리한다면 추가할수 있겠다.
그리고 비선형성을 사용하기 위해서 계산 결과를 tanh 함수의 입력으로 사용하면 새로운 (현재 타임 스탭의) 은닉 상태 $h_t$를 얻을수가 있고, 출력 $y_t$는 현재 상태 $h_{t}$를 다른 가중치 행렬 $W_{ht}$와 곱함으로서 선형 변환하여 나오게 된다
지금까지 Elman RNN에 대한 정의를 보면서 어떻게 동작하는건지 이해할수 있겠다.

순환 신경망이 어떻게 동작하는지 보는 다른 좋은 방법으로 계산그래프를 이용해서 알아보면 좋겠다. 순환 신경망을 시간 변화에 따라서 쭉 풀어보면, 시퀀스 맨 처음에는 시쿼스 첫번째 원소인 $x_{1}$이 초기 입력으로 들어온다. 여기에 초기 은닉 상태 $h_{0}$가 필요한데 일반적으로 초기 은닉 상태는 0으로 설정하고, 어떤 경우에는 이것도 학습 가능한 파라미터로 놓고 학습해 나가기도 한다.
하지만 초기 은닉 상태 값을 모두 0으로 설정해도 잘 동작한다. 이렇게 초기 은닉 상태와 시퀀스의 첫번째 원소가 주어질때

이 초기 은닉 상태 $h_{0}$와 입력 $x_{1}$를 순환 관계 함수 $f_{w}$에 넣어서 첫번쨰 은닉상태인 $h_{1}$을 구할수가 있고,

이렇게 구한 첫번쨰 은닉 상태 $h_{1}$과 시퀀스의 다음 요소인 $x_{2}$를 동일한 함수 $f_{w}$에 넣어 다음 은닉 상태를 만들 수가 있겠다.

그리고 이런 식으로 계속 진행 되겠다.

여기서 중요한 건은 모든 타임 스탭, 시퀀스들은 동일한 가중치 행렬을 사용한다는 점이다. 위 그림의 계산그래프를 보면 확실하게 볼수 있는데 가중치 행렬 W 노드 하나가 모든 타임 스탭에서 사용되고 있다.
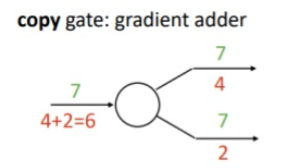
이번에는 역전파 과정에서 어떻게 되는지 생각해볼건데, 카피 노드의 경우 순전파 때는 한 노드를 여러개로 복사하는 역할을 했었고, 역전파때는 업스트림 그라디언트들을 합하여 다운스트림 그라디언트로 보내주는 역활을 하는데, 이 점이 이게 과제 4번 순환 신경망 구현에서 중요하다.
그리고 모든 타임 스탭에서 같은 가중치 행렬을 사용하다보니 어떤 길이의 시퀀스이던 간에 순환 신경망으로 처리할수가 있으며, 시퀀스 요소가 2개인 경우가 들어와도 이 그래프는 두번의 타임 스탭만 진행하면 되고, 시퀀스의 길이가 100이라면 이 그때는 100번 타임 스탭만큼 그래프가 진행되면 되겠다.
그래서 입력으로 받는 시퀀스의 길이가 중요하지 않으며 같은 순환 신경망, 특정 길이의 시퀀스 처리에 같은 가중치 행렬을 사용해서 처리할수 있겠다.
지금까지 본 내용들이 순환 신경망의 기본적인 연산 과정으로 아까 1 대 다, 다 대 다 같은 여러가지 종류의 시퀀스 문제들을 봤다시피 이제는 어떻게 다양한 시퀀스 문제들을 처리할수 있는 순환 신경망을 구현해서 사용하는지를 살펴보자.

이번 슬라이드는 입력 시퀀스를 받아서 각 시점에서 출력을 내보내는 다대다 문제로 예를 들어 비디오 문제가 있는데, 비디오의 모든 프레임을 분류하는 경우라고 할수 있겠다. 여기서도 가중치 행렬 W가 주어지고 이 가중치 행렬을 모든 타임 스탭에서 출력 y를 계산하는데 사용된다.

그리고 라벨을 가지고 있는 경우에 라벨을 가지고 학습시키기 위해서 시퀀스의 매 타임 스탭마다 비용 함수를 사용할 것이고, 비디오 분류같은 문제라면 시퀀스의 모든 시점에서 분류 결정을 하게 될건데, 교차 엔트로피 함수로 실제 라벨 ground truth와 예측 결과에 대한 비용을 계산하여 학습 시킬수가 있겠다.

최종 비용을 구하기 위해서 모든 시간 때의 비용들을 합하여 구할수가 있겠고 이 최종 비용을 역전파 하는데 쓸수 있겠다. 이 예시는 하나의 타임 스탭 때 하나의 출력을 내보내는 다 대 다 순환 신경망의 완전 계산그래프이다.

이번에는 다 대 일 상황을 다뤄본다고 하면 예를 들어 비디오 시퀀스를 입력받아 하나의 라벨로 분류하는 비디오 문제라는 경우를 다룬다고하자. 이 경우에는 시퀀스의 맨 끝에서 순환 신경망의 최종 은닉 상태를 가지고 연산해서 하나의 예측 값을 구하면 된다.
그리고 이 순환 신경망의 최종 은닉 상태는 전체 입력 시퀀스에 영향을 받으며, 우리가 구한 최종 은닉 상태는 신경망이 전체 시퀀스를 가지고 분류 결정을 하기위해서 알아야하는 모든 정보들을 정리 한 것이라고 보면 된다.

다른 경우로 이미지 캡셔닝 같이 하나의 이미지를 입력으로 받아 단어들의 시퀀스를 출력하는 일 대 다 문제가 있으며 순환 신경망을 이용해서 처리할수가 있다. 이 경우 단일 입력 x는 맨 앞에서만 들어가고, 순환 (관계) 함수를 사용해서 전체 출력 시퀀스를 만들어 낸다.

또 다른 순환 신경망을 이용한 예시로는 sequence to seqeuence seq2seq가 있는데, 입력 시퀀스를 처리해서 길이가 다른 입력 시퀀스를 만들어내는 것같은 기계 번역같은 경우가 있다. 여기서 입력으로 영어 단어 시퀀스가 들어오고 출력으로는 프랑스 단어 시퀀스가 내보내는 그러니까 문장 번역을 수행하도록 시킬수가 있다.
프랑스 말이랑 영어 말이나 항상 같은 길이의 문장으로 동일한 의미를 표현하도록 번역을 할수 없다보니, 입력 시퀀스를 처리해서 다른 길이의 출력 시퀀스를 만들어내는 순환 신경망을 만들어야 한다.
이런 서로 다른 길이의 입력, 출력 시퀀스를 내보내는 순환 신경망을보고 seq2seq rnn 아키텍처라고 부른다. 이 아키텍처는 기본적으로 다 대 일 순환 신경망 구조를 사용하여 구한 결과를 다른 일 대 다 순환 신경망에 전파함으로서 동작시킨다.
지금 보고있는 게 인코더라고 부르는 순환 신경망으로 시퀀스를 입력받아서 이 경우에는 영어 문장을 입력으로 받아서 매 시간마다 단어 하나 하나씩을 처리할것이고, 시퀀스 전체 내용을 처리한 후에 내용들은 맨 끝에 있는 은닉 벡터로 요약/정리가 된다.
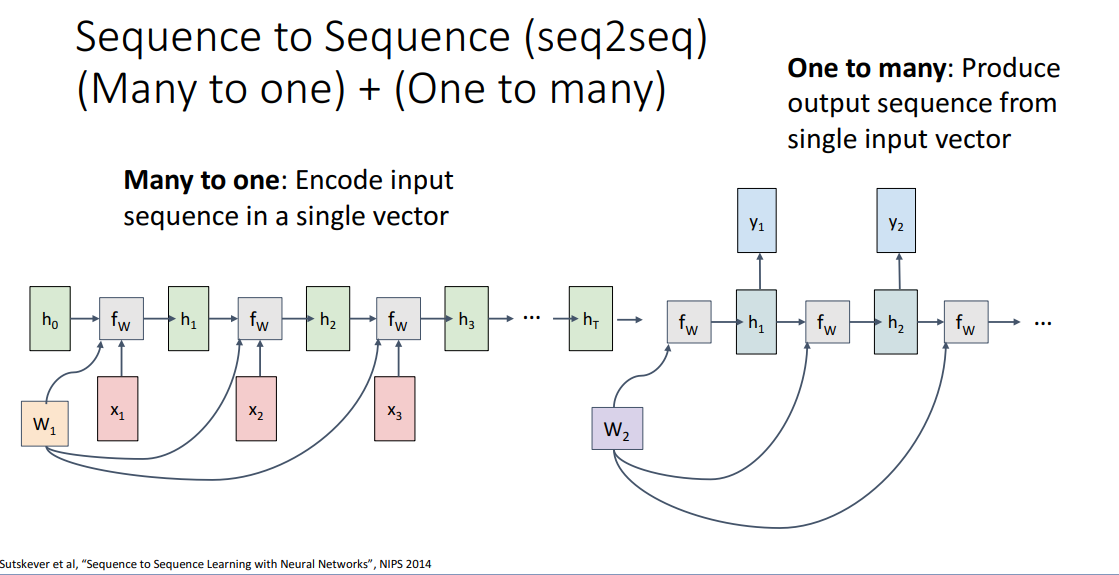
이렇게 인코더의 맨 끝에서 구한 은닉 벡터는 디코더라고 부르는 두번째 순환 신경망의 단일 입력으로 사용되며, 이 디코더 신경망은 첫번째 인코더 신경망으로부터 단일 벡터를 입력받아 출력으로 여러 단어들, 시퀀스를 출력하다보니 일 대 다 신경망이 되겠다.
이 그림이 디코더에 대한 계산그래프로 인코더와 디코더는 서로 다른 가중치 행렬을 사용하며, 이런 형태가 대표적인 시퀀스 투 시퀀스 모델 형태라고 할수 있겠다.
(질문) 인코더와 디코더로 나눠서 처리하는 이유는 무엇인가?
여기서 문제는 출력 토큰의 개수가 입력 토큰의 개수와 얼마나 달라야하는지 모른다는 점인데 우선 영어 문장을 처리해서 프랑스 문장으로 만든다고 하자. 하지만 출력시킬 단어 갯수를 입력의 단어 개수와 얼마나 다르게/차이나게 할지 알 수 없으므로 나눠서 다루는게 중요하다.
한번 인코더와 디코더 둘다 동일한 가중치 행렬을 사용한다고 생각해보자. 전체 입력 시퀀스가 주어지고 k번 타음 스탭만큼 진행하고나서, 나머지 k번 타임 스탭에서는 별도의 입력 없이 진행되서 출력을 얻을수가 있겠다. 아까 질문은 디코더에서 얼마나 많은 토큰들이 필요하느냐인데, 이후에 나올 슬라이드를 보면서 자세히 다뤄보겠다.
'번역 > 컴퓨터비전딥러닝' 카테고리의 다른 글
| 딥러닝비전 12. 순환 신경망 - 4. 텍스트 생성과 은닉 유닛 해석 (0) | 2021.03.13 |
|---|---|
| 딥러닝비전 12. 순환 신경망 - 3. 언어 모델과 역전파 (0) | 2021.03.12 |
| 딥러닝비전 12. 순환 신경망 - 1. 이전 시간 복습과 순환 신경망 활용 (0) | 2021.03.09 |
| 딥러닝비전 11. 신경망 학습하기 파트 2 - 3. 학습 후 할 수 있는 일 2(전이학습) (0) | 2021.03.09 |
| 딥러닝비전 11. 신경망 학습하기 파트 2 - 3. 학습 후 할 수 있는 일 (0) | 2021.03.07 |