
셀프 어텐션 레이어는 신경망에서 사용할수 있는 새로운 종류의 레이어로, 셀프 어텐션 레이어를 사용한 합성곱 신경망을 만든 예시를 살펴보자.
이 합성곱 신경망은 귀여운 고양이 이미지를 입력으로 받아 합성곱 레이어들의 출력으로 어떤 벡터의 그리드 c x h x w, 가로 h, 세로 w, 채널 수가 c인 출력을 만들어낸다.

그러면 이제 세개의 1 x 1 합성곱 연산을해서 특징 그리드들을 쿼리들의 그리드, 키의 그리드, 값의 그리드들로 변환하자. 각 1 x 1 합성곱 연산들은 학습 과정으로 얻은 고유의 가중치와 편향값을 가지고 있어, 병렬로 분할시킨다.

이제 쿼리와 키를 내적 한 뒤 소프트 맥스 함수를 적용하여 어텐션 가중치를 구할건데, 이 결과는 입력 이미지에서 한 지점이 주어질때 이에 대해 다른 모든 지점들은 얼마나 주의를 기울여야 하는 정도를 나타낸다. 그렇다보니 크기가 (h x w) x (h x w)의 아주 큰 어텐션 가중치 행렬이 만들어진다.

이 어텐션 가중치를 값 벡터들과 선형 결합을 시키겠다. 이 선형 결합으로 새로운 특징 벡터의 그리드를 만들어 내고, 그 출력 그리드의 모든 위치들은 입력 그리드의 모든 위치에의해 정해진다/영향을 받겠다. 이 과정은 기존의 합성곱과 상당히 다른 연산과정이라 할수 있겠다.
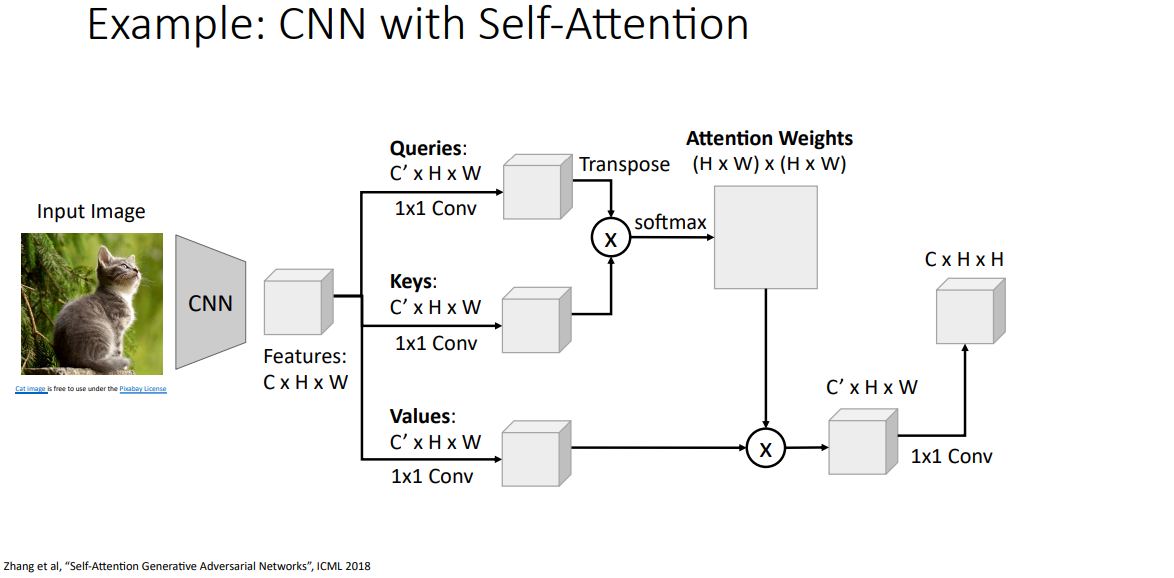
실제 사용시에 종종 사람들은 이 어텐션 연산을 마친 후에 추가적인 1 x 1 합성곱 연산을 하기도 하고,

이 셀프 어텐션 연산 전체 주위로 잔류 연결/스킵 커넥션을 추가하는 경우도 많습니다. 그래서 이런 요소들을 한데 합쳐서 새로운 셀프 어텐션 모듈을 만들어서 신경망에다가 넣어서 사용할수 있고, 이렇게 만든 신경망은 합성곱 연산 뿐만 아니라 더 셀프 어텐션을 할수 있겠습니다.

여기서 기본적으로 다뤄보면 좋은 것으로 신경망에서 벡터의 시퀀스를 처리하는데 사용할수 있는 방법으로 3가지가 있습니다. 가장 흔한 방법은 이전 강의에서 다루었던 순환 신경망이 있는데, 입력 벡터들의 시퀀스 x가 주어지면, 출력 벡터 y의 시퀀스를 만들어 내었습니다.
LSTM과 같은 순환 신경망을 사용할때 좋은점은 아주 긴 시퀀스를 다루는데 좋은것으로, 아주 긴 시퀀스에서도 정보를 잘 전달할수 있습니다. 특히 RNN 레이어의 최종 출력 혹은 최종 은닉 상태 y_t는 전체 입력 시퀀스로 구하게 되요. 단일 rnn 레이어는 전체 입력 시퀀스를 요약한 것이라고 볼수 있겠습니다.
하지만 RNN은 몇가지 문제점을 가지고 있는데, 이들을 은닉 상태 1을 계산한다음 2를 계산하고, 3을 계산하고, 4를 계산하는 데이터에 순차적으로 의존적이라 병렬화 시키기가 어렵습니다.
이전에 gpu 강의를 다시 떠올려보면, 아주 큰 신경망을 만들때 GPU의 방대한 병렬 연산의 이점을 가질수면 좋겠지만 RNN은 그런 하드웨어로 병렬 연산을 하는데 좋지 않아 큰 RNN 모델을 만드는데 문제가 있습니다.

또 다른 시퀀스를 처리하는 방법으로 일차원 합성곱 연산이 있습니다. 일차원 합성곱 연산을 입력 시퀀스에 대해서 슬라이드 시켜, 출력 시퀀스의 각 지점들은 입력 시퀀스의 세 이웃으로 구할수 있겠습니다.
컨볼루션을 이용하여 시퀀스를 처리하는 신경망의 경우, RNN이 순차 의존성을 가지넋과는 달리 시퀀스의 각 출력 원소들이 독립적으로 계산되다보니 매우 병렬화하기 좋은 점을 가지고 있습니다.
하지만 합성곱 연산을 이용한경우 단점은 매우 긴 시퀀스를 잘 처리하지 못한다는 점인데, 출력을 전체 시퀀스로 구하고자 하는경우, 단일 합성곱 레이어로는 구할수 없으며 시퀀스의 모든 지점을 보기 위해서 아주 많은 레이어를 쌓아야 합니다. 그런 이유로 합성곱으로 시퀀스를 처리하기는 어려우나, 병렬화하기 좋다는 장점이 있습니다.

이번에 다뤄볼 방법으로 셀프 어텐션이 있습니다. 이 방법은 앞서 본 결점들을 극복한 시퀀스나 벡터의 집합을 처리할수 있는 새로운 메커니즘으로, 셀프 어텐션은 주어진 벡터의 집합으로 각 벡터와 다른 모든 벡터들을 비교하다보니 긴 시퀀스를 잘 처리할수 있습니다. RNN과 비슷하게 단일 셀프 어텐션 레이어는 각 출력들은 각 입력에 영향을 받겠습니다.
뿐만아니라 셀프 어텐션은 합성곱 연산과 같이 매우 병렬화 하기 좋다는 장점을 가지고 있습니다. 몇 슬라이드 전에 본 셀프 어텐션 구현 과정을 보면, 셀프 어텐션은 크지만 몇개의 행렬 곱 연산에다가 소프트 맥스 같은게 추가되다보니 아주아주 병렬화 하기가 좋으며, GPU에서 연산시키기에 적합하다고 할수 있겠습니다.
셀프 어텐션은 합성곱과 순환 신경망의 단점을 극복하여 시퀀스나 집합을 처리할수있는 대안 메커니즘으로 사용되고 있습니다. 하지만 단점으로는 아주 많은 메모리 공간을 사용한다는 점이나 시간이 갈수록 GPU 메모리 공간이 더 커지고 있으므로 이런 문제는 무시해도 되겠습니다.

여러분들이 신경망으로 시퀀스를 처리하다가 어떤 문제를 만날떄, rnn, 컨볼루션, 셀프 어텐션중에서 어떤걸 사용하느게 좋을까요? 몇년 전에 있었던 한 유명한 논문으로 "Attention is all you need"가 있으며, 셀프 어텐션 만으로도 시퀀스를 처리하는 신경망을 만들수가 있겠습니다.
'번역 > 컴퓨터비전딥러닝' 카테고리의 다른 글
| 딥러닝비전 14. 합성곱 신경망의 시각화와 이해 - 1. 필터 시각화와 차원 축소 (0) | 2021.03.25 |
|---|---|
| 딥러닝비전 13. 어텐션 - 6. 트랜스포머 (0) | 2021.03.22 |
| 딥러닝비전 13. 어텐션 - 4. 셀프 어텐션 (0) | 2021.03.19 |
| 딥러닝비전 13. 어텐션 - 3. 어텐션 레이어 (0) | 2021.03.19 |
| 딥러닝비전 13. 어텐션 - 2. RNN과 어텐션을 이용한 이미지 캡셔닝 (0) | 2021.03.18 |