
지금까지 다뤄온 컴퓨터 비전 문제는 기본적으로 이미지 분류 문제들을 위로 다뤄봤다. 단일 이미지를 합성곱 모델에다가 넣어서 이미지의 카테고리 라벨을 얻었다. 고양인지, 강아지인지, 차인지 등 이와 같이 단일 카테고리 라벨을 얻었다. 이 작업은 수많은 응용분야에서 유용하며, 딥러닝 파이프라인 전체를 어떻게 만들고 학습해나가는지에도 좋았다. 하지만 이미지 분류 문제는 컴퓨터 비전에서 다루는 수많은 작업들중 하나일 뿐이다.

여기에 컴퓨터 비전에서 일하는 사람들이 다루는 작업들을 계층적으로 정리한건데 이미지와 객체를 다양한 방식으로 식별하려고 하고 있다. 이번과 다음 강의에서는 이미지 상 객체의 공간적 존재 여부를 식별하는 다양한 방법들을 살펴볼것이고, 고전적인 이미지 분류 문제처럼 각 이미지의 픽셀별로 카테고리 라벨을 붙이는게 아니라 주어진 이미지에 대한 카테고리 라벨을 구해보겠다.

다른 컴퓨터 비전 작업으로 하나의 카테고리 라벨을 주는게 아니라 이미지의 여러 다른 부분에 다른 카테고리를 주고싶을 수도 있다. 이번과 다음 강의에서 이러한 작업들에 대해서 다룰것이고, 이번 시간에는 객체 탐지라고 하는 작업에 대해서 다뤄볼 것이고 컴퓨터 비전의 수 많은 응용분야에서 핵심이기도 하다.

객체 탐지란 입력 이미지를 주었을때 출력으로 검출한 객체들을 가지는 작업이 되겠다. 검출한 객체들은 여러가지들을 출력하는데 그 중 하나는 그 검출된 객체의 카테고리이고, 다른 하나는 바운딩 박스로 이미지 상에 공간 어디에 위치하는지에 대한 정보가 되겠다. 이 바운딩 박스는 4개의 수로 이뤄져있는데 박스의 중앙점 x, y와 폭과 높이 w, h가 있다.
모델이 회전된 바운딩 박스를 만들어 낼수도 있긴하지만 일반적인 객체 탐지 작업의 경우 그러지 않고, 축과 나란한 박스를 만들어 내므로 위의 4개의 실수로 정의할수 있겠다. 이 작업은 이미지 분류와 비교해보면 바뀐게 별로 없어보이지만 얼마나 어려울까? 여기서 우리가 할일은 이 박스와 카테고리 라벨만 구하면 되지만 이건 아주 어려운 작업이다.

객체 검출에서 우리가 다뤄야 할 문제들 중 하나는 다중 출력을 내야하는 것인데, 이미지 분류의 경우 하나의 이미지에 대해서 하나의 분류 결과를 냈으면 되었지만 이미지에서 검출된 객체 전체의 분류 결과를 만들어 내야 한다. 그래서 모델을 만들때 고정된 크기의 출력이 아닌 가변 크기의 출력을 내도록 하여야 하므로 어려운 일이 되겠다.
또 다른 문제로 각 객체들은 두 출력 값을 가지고 있는데 하나는 카테고리 라벨과 다른 하나는 바운딩 박스가 있다. 그래서 바운딩 박스를 구할수 있도록 하는 과정이 필요하다. 객체 탐지의 다른 문제는 계산 비용 문제로 상대적으로 고해상도 이미지에서의 처리가 필요하다. 대부분 이미지 분류의 경우 저 해상도 이미지로도 충분하였지만 객체 탐지의 경우 이미지안에 있는 여러 객체들을 식별해야하므로, 객체를 탐지할 만큼 충분한 이미지의 공간적 크기(해상도)가 필요하다. 객체 탐지 모델의 구체적인 예시로 이미지 해상도는 800 x 600정도로 이미지 분류에서 사용했던것보다 크다. 그래서 학습에 오랜 시간이 걸리고, 계산 비용으로 인해 객체 탐지가 훨씬 어렵게 되겠다.
하지만 객체 탐지는 매우 유용한 문제로 우리가 만들고자 하는 많은 시스템에서 사용될수가 있겠다. 예시로 자율주행 차가 있겠고, 자율 주행차의 비전 시스템을 만든다면 차 주위에 무엇이 있는지 알아야할것이고 이게 매우 중요한 문제다보니 이미지로 단일 카테고리만 필요한게 아니라 전체 객체들을 구하여야 하겠다. 기본적으로 이미지 분류 다음에는 객체 탐지가 컴퓨터 비전 분야에서 두번째로 핵심적인 문제라고 할수 있겠다.

이미지의 여러 객체가 아니라 단일 객체를 찾는 경우로 조금 단순하게 살펴봅시다. 단일 이미지를 탐지하는 경우 단순하게 할수가 있습니다. 왼쪽 이미지가 있고, 알렉스넷이라던가 선호하는 신경망 아키텍처에 넣으면 이미지의 벡터 표현 결과가 나오겠습니다.

벡터를 가지고 나뭇가지 형태로 분기해서 할수 있는 일을 보면 하나의 가지로 내려가면 이미지 분류에 사용할수도 있는데, 이건 이전에 살펴봣던 이미지 분류 작업과 동일하다고 할수 있으며 카테고리별 스코어를 구하고 소프트맥스 로스로 올바른 카테고리를 구합니다.

또 다른 가지로 내려가서 두번째 가지에서는 똑같이 이미지의 벡터 표현 결과가 들어가지만 4개의 출력을 갖는 완전 연결 계층을 가진다. 이 4개의 수는 바운딩 박스의 좌표계값들로 이 값들은 L2같은 회귀 비용을 사용해서 학습할수가 있겠고, 실제 바운딩 박스의 좌표계값과 예측한 바운딩 박스의 좌표계값의 차이로 학습 시킬수가 있다.
이제 문제는 두개의 비용 함수를 사용한다는 점인데, 이렇게 된 이유는 우리가 두 개의 모델이 두개를 예측하도록 하였기 때문인데 하나는 라벨 카테고리와 다른 하나는 바운딩 박스의 위치가 되겠다. 이 두개를 합친 비용함수를 구할수도 있지만 그라디언트 하강을 계산하기 위해선 단일한 스칼라 비용값이 나와야 한다. 하지만 우리는 여러개의 로스를 처리하는 방법을 모르고 있다.

이 문제를 극복하기 위해서 서로 다른 비용들을 가중합하여 최종 비용을 구하면 되겠다. 비용의 가중합을 구하는 이유는 소프트 맥스 비용과 L2 회귀 비용 사이의 중요도를 서로 압도하지 않도록 미세 조정할 필요가 있기 때문이다. 이 다중 비용 함수를 사용하는 아이디어는 하나의 신경망이 여러개를 학습을 해야하는 경우 사용한다.

그래서 하나의 비용 함수뿐만이 아니라 다른 예측할 비용함수를 추가하고 이들을 가중합을 구함으로서 신경망이 다중 출력 결과를 학습할수 있도록 만들수가 있다. 이러한 일반적인 구조를 다중 작업 비용 함수라 부른다. 신경망이 다른 작업들을 한번에 학습할수 있고, 끝에 단일한 비용 함수로 만들어내기 때문이다.

이걸 실제로 쓰기 위해선 이 백본 합성곱 신경망을 이미지넷 분류셋으로 선학습한 후에 네트워크 전체를 다중 비용 위치 추정 문제로 미세조정을 할수가 있겠다. 객체 탐색에 있어서 바보같은 방법인데, 직관적이며 완전 연결신경망을 끝내다가 붙여 박스 좌표계값들을 추정해낸다. 이 상대적으로 간단한 방법은 꽤 잘 동작하지만 이미지에서 하나의 객체만 탐지하는 경우에만 사용 가능하다.

하지만 실제 이미지에서는 탐지할 객체가 여러개이므로 일반적인 용도로 사용하는데는 적합하지 않습니다.

일반적인 경우 이미지들은 탐지해야할 다양한 개수의 객체들을 가지고 있습니다. 이 고양이 이미지의 경우 한 객체만 탐지해서 고양이의 바운딩 박스에 대한 4개의 수를 추정해내면 되지만. 중간의 이미지는 3개의 객체를 탐지해야하는데 2 강아지랑 1고양이로 3 x 4 = 12개의 수를 추정해내야되요. (슬라이드는 버그)
맨 아래의 사진에는 귀여운 오리들이 엄마 오리들을 따라가고 있는데 아주 많은 오리들이 있죠. 셀수도 없고 아무튼 아주 많습니다. 하지만 우리가 만든 신경망은 이 모든 오리들을 다 탐지해낼수 있어야 합니다. 이 경우에는 아주 많은 수의 결과를 구해내야 합니다. 그래서 우리 모델이 다양한 개수의 객체들을 출력 해낼수 있는 메커니즘이 필요합니다.

그래서 이걸 할수 있는 상대적으로 쉬운 방법으로 슬라이딩 윈도우를 이용한 객체 탐지 방법이 있습니다. 여기에 개념을 볼수 있는데 합성곱 신경망으로 분류 작업을 할건데, 이 합성곱 신경망은 입력 이미지의 윈도우/서브리전을 분류를 합니다. c개의 카테고리로 분류하는 경우 c + 1개의 출력을 할수가 있는데 여기서 추가되는 1개의 경우는 배경을 의미하며 이미지 탐지 문제를 이미지 분류 문제로 만들기 위함입니다.
이 합성곱 신경망을 이미지의 수많은 영역들에 적용해서 서 강아지인지 고양이인지 혹은 아무것도 없으면 배경으로 분류해냅니다. 이 슬라이딩 윈도우 합성곱 신경망 객체 검출기를 파란색 영역에다가 사용해보면 아무런 객체가 없으니 이 이영역은 배경으로 분류하겠습니다.

이 영역을 슬라이드시키고, 이 영역은 강아지를 잘 감싸고 있으므로 강아지가 있다고 할수 있겠습니다.

여기에는 강아지가

여기에는 고양이가 있다고 할수 있겠죠. 그래서 이런 객체 검출기를가지고 다양한 영역들에 슬라이드 시키기고 각 영역을 합성곱 신경망에 넣어 객체인지 배경인지 알수있겠습니다. 이건 꽤 간단한 방법이지만 문제가 있습니다.

H x W 크기의 이미지에 바운딩 박스가 몇개가 존재할수 있을까요?

바운딩 박스의 크기가 h x w라고 할때, (W - w + 1) * (H - h + 1)개의 가능한 x, y의 위치 경우의 수가 있으며

고정된 크기의 박스가 아니라 모든 가능한 크기를 고려했을때 이와 같은 이차식같은 형태의 가능한 경우의 수들이 존재합니다.

이게 얼마나 나쁘냐면 800 x 600 크기의 이미지가 있으면 ~58M개의 박스가 존재할수 있으며, 집약된 슬라이딩 윈도우 방식은 실제로 사용할수가 없겠습니다. 그래서 다른 객체 검출 방식이 필요해요.

영역 제안 이라고 하는 방법이 있습니다. 가능한 모든 영역에 대해서 객체 검출기로 평가할수없다보니, 이미지에서 후부 영역들을 만들어내는 알고리즘을 사용할수 있는데, 후보 영역들은 상대적으로 작은 서브리전이지만 이미지에서 객체를 높은 확률을 가지고 있습니다.
몇년전에 수 많은 논문에서 이런 후보 영역들을 만들어내는 메커니즘이 소개되었는데 이들을 영역 제안 resion proposal이라고 부릅니다. 이게 어떻게 동작하는지 깊이 들어가지는 않을건데 결국에 이 방식들이 신경망으로 대체되었기 때문입니다.
이런 초기 영역 제안 방식은 입력 이미지에다가 이미지 프로세싱을 수행했다고 할수 있는데, 이미지에 블롭같은 영역이나 에지 영역이나 다른 로레벨 이미지 프로세싱 기법으로 객체를 높은 확률로 가졌을만한 영역들을 찾아내었습니다.
이런 방법들중에서 가장 유명한것 중하나로 선택적 탐색 selective search가 있습니다. 이 알고리즘은 cpu로도 돌릴수 있는데 이미지당 2000개의 리전을 몇초만에 알려줍니다. 이 2000개의 제안 영역들은 우리가 높은 확률로 있다고 보고 주의를 기울일만한 객체들을 가지고 있어요. 이러한 영역 제안 방법은 심층 신경망을 이용해서 실제 사용가능한 객체 검출기로 직관적으로 학습시킬수가 있습니다.

매우 유명한 논문으로 RCNN이 있습니다. 여기서 R은 region based를 뜻하며 이 논문은 Region based CNN이라고 부릅니다. 이 논문은 2014년도에 나온 매우 영향력이 컸던 논문이라고 할수 있겠습니다. 하지만 이 방법은 꽤 이해하기 쉽게 동작해요 우리할 일은 일단 이 입력 이미지를

선택적 탐색과 같은 영역 제안 방법을 돌리는데, 선택적 탐색법은 2000개의 후보 제안 영역들을 줍니다. 2000개는 많으니 여기선 3개만 표시하겠습니다.

각 후보 영역들은 서로 다른 크기나 비를 가지고 있을것이고 각 제안 영역들을 224 x 224의 고정 크기로 변환시키겠습니다.

각 후보 영역들을 독립적으로 합성곱 신경망에다가 돌리고,

그러면 각 합성곱 신경망은 분류 스코어를 출력하겠습니. 이 c + 1개의 분류 스코어가 이게 배경인지 혹은 배경이 아니고 무엇인지 알려주겠습니다. 여기서 문제가 있는데, 이 선택적 탐색으로 얻은 제안 영역들이 실제로 우리가 탐지하고자 하는것과 일치하지 않을수가 있습니다. 왜냐면 여기서 구하는 전체 바운딩 박스들을 구하는 메커니즘은 블랙박스인 선택적 탐색 방법을 사용하기 때문에 박스를 구하는데 있어서 학습 과정이 존재하지 않습니다.

이 문제를 극복하기 위해서 멀티태스크 비용같은 방법을 사용해서 cnn이 추가 정보를 내도록 변경시켜, 예측한 바운딩 박스가 실제 우리가 원하는 박스를 출력하도록 변환을 추가하겠습니다.
여기서 짚고 넘어가고 싶은 부분은 바운딩 박스 회귀는 우리가 처음에 얻은게 아니라 입력으로 주어진 제안 영역을 변경시켜 얻은 것입니다. 제안 영역들도 좋긴 하지만 더 물체를 잘 찾아내서 개선할 수 있도록 할것이고, 바운딩 박스는 4개의 수로 모수화 할수 있다보니 구한 바운딩 박스와의 차이(transform/delta)도 4개의 수로 정리할수 있겠습니다.

바운딩 박스 변환의 다양한 모수화 방법이 있는데, 가장 흔하게 사용되는건 우측에 있는게 있겠습니다. 제안 영역이 주어지면, 이 제안 영역인 px, py, ph, pw를 가지고 있고, 이걸 4개의 수 tx, ty, th, tw로 변환시키고, 최종 결과 output box는 주어진 제안 영역에다가 변환 값을 반영하여 구하겠습니다.
여기서 있는 모수값들은 박스 크기에 비례하여 평행이동시키며, 로그 공간상에서 크기 조정을 하겠습니다. 제안 영역의 폭과 높이의 스케일을 조정시킬것인데, cnn에 넣기 전의 입력 영역으로 다시 되돌려 주기 위함입니다.
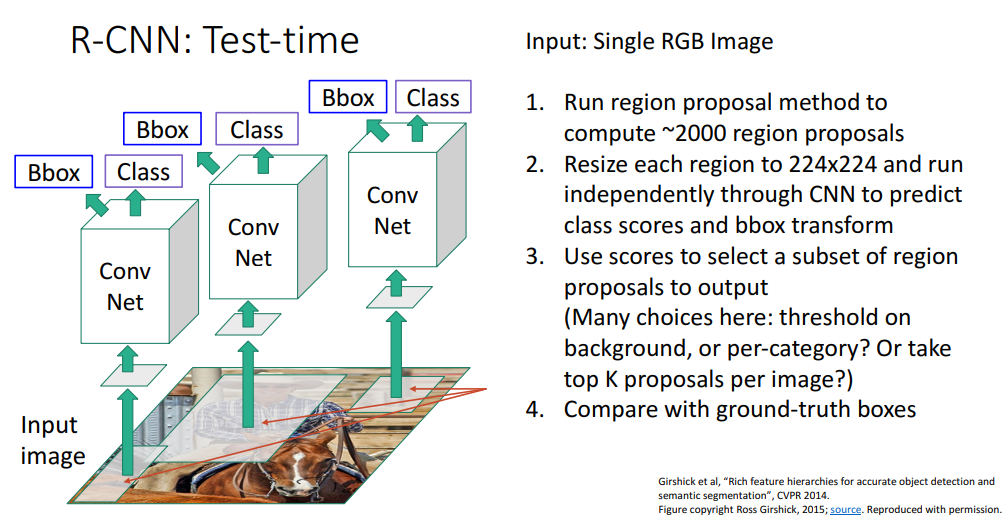
지금까지 본 내용들이 우리가 처음으로본 합성곱 신경망을 이용한 객체 탐지기가 되겠습니다. 이제 테스트 타임의 파이프라인을 살펴보면 이렇게 생겼는데, 싱글 RGB 이미지를 선택적 탐색같은 영역 제안 방법을 돌려서 2000개 정도의 제안 영역들을 구합니다.
각 제안 영역들을 구하면 고정된 크기로 224 x 224로 변환하고 독립적으로 합성곱 신경망으로 돌려서 카테고리를 구합니다. 거기다가 BBox 변환으로 기존의 제안 영역의 좌표를 고쳐줍시다.
이제 테스트 타임에는 어플리케이션에 쓸수 있도록 유한개의 셋을 구하면 되겠는데, 여기서 다양한 방법들이 있겠지만 우리가 사용한 어플리케이션에 따라서 고르면 되겠습니다. 여기서 사용해볼수 있는 방법으로 전체 영역들의 예측 스코어로 박스 셋을 구하고 싶을수도 있을텐데 한가지 방법은 이미지당 10개의 객체들을 구하길 원한다면 카테고리가 무엇인지 신경쓰지말고, 백그라운드 스코어로 임계화를하는데 배경 스코어가 가장 낮은 10개를 최종 예측 결과로 사용하면 됩니다.
다른 방법으로 카테고리별 임계치를 설정하는 방법도 있는데 분류신경망은 배경 뿐만이 아니라 전체 카테고리 스코어도 출력을 하기 때문이며, 또 다른 옵션으로 특정한 임계치를 넘는 카테고리의 박스를 최종 결과셋으로 출력해도 되겠습니다.
여기서 사용하는 합성곱 신경망은 모두 같은 가중치를 공유하고 있으며, 제안 영역들에 적용됩니다. 만약 이 합성곱 신경망들이 가중치를 공유하지 않으면 잘 동작하지 않을수가 있는데, 이미지마다 서로 다른 개수의 제안 영역들을 가질수 있고, 이미지당 2000개의 고정된 개수의 제안 영역들을 가진다고해도 개별적으로 다 돌리기 어렵기 때문입니다.
그래서 지금까지 이미지를 입력으로 주고 바운딩 박스 셋을 출력으로 하는 실용적인 알고리즘에 대해서 살펴보았는데, 우리가 구한 박스들이 실제로 우리가 구해야 하는 박스와 비슷한지 다른 사람의 것과 성능이 더 나아졌는지 비교할수 있도록 평가할 필요가 있습니다.

그걸 하기 위해선 두 바운딩 박스를 비교하는 메커니즘이 필요합니다. 위와 같은 귀여운 강아지 이미지가 있으면 그린 박스는 시스템이 실제 구해야하는 박스고, 우리의 알고리즘이 구한 박스는 블루 박스가 되겠습니다. 그리고 이들을 파란 상자가 녹색 상자랑 잘 맞는지 비교를 할 방법이 필요합니다.

일반적으로 두 바운딩 박스를 비교하기 위해서 사용하는 방법은 Intersection over Union IoU라는 척도가 있습니다. 이걸 다른 상황에서는 jaccard similarity/index라고도 합니다. 하지만 객체 탐지에선 IoU라고 부릅니다. 이 값은 두 바운딩 박스의 비슷한 정도를 나타내는데, 두 박스의 겹치는 부분 intersection(주황)과 두 박스를 합한 영역 union(보라)의 비율로 계산합니다.

이 예시에서 IoU는 0.54가 되는데 항상 0과 1사이의 값이되며, 두 박스가 완전히 일치하는 경우 이 비율은 1이 되고, 완전히 겹치는 부분이 없으면 0이 되겠습니다. 일반적으로 IoU는 0과 1사이로 두 박스가 더 잘 매치될수록 더 큰 수가 나옵니다.
IoU가 0.5보다 크다면 그래도 두 바운딩 박스가 잘 매치되고 있구나라고 볼수 있는데, 0.54면 완벽하지는 않지만 객체의 중요한 부분을 잘 찾았다고 볼수 있겠습니ㅏㄷ.
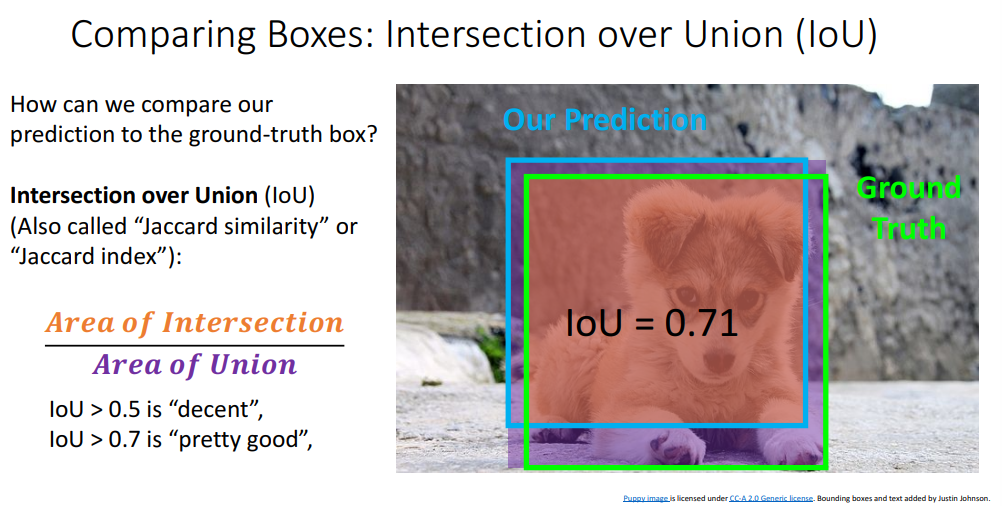
0.7은 아주 잘찾은것이며, 약간 에러는 있지만 물체 위치를 잘 추정해내었다고 볼수 있습니다.

0.9 이상인 경우 거의 완벽하다고 할수 있겠습니다. iou라는 척도는 두 바운딩 박스를 비교하는 다양한 상황에서 사용하고 있습니다.
'번역 > 컴퓨터비전딥러닝' 카테고리의 다른 글
| 딥러닝비전 15. 객체 검출 - 3. Fast R-CNN, 특징맵 자르기, 성능 비교 (0) | 2021.04.05 |
|---|---|
| 딥러닝비전 15. 객체 검출 - 2.비최대 억제를 이용한 겹치는 영역 제거, 객체 검출기 평가 척도 mAP (0) | 2021.03.30 |
| 딥러닝비전 14. 합성곱 신경망의 시각화와 이해 - 2. 활성 시각화, 최대활성패치, 중요 픽셀 시각화 (0) | 2021.03.25 |
| 딥러닝비전 14. 합성곱 신경망의 시각화와 이해 - 1. 필터 시각화와 차원 축소 (0) | 2021.03.25 |
| 딥러닝비전 13. 어텐션 - 6. 트랜스포머 (0) | 2021.03.22 |