
지금까지 어텐션 메커니즘으로 다양한 작업들에 사용한 경우들을 알아보았습니다. 하지만 최근 몇 년간 연구에서 어떤 일들이 있었을까요? 많은 작업에서 유용해보이다보니 이 메커니즘을 다양한 타입의 문제에서 적용시키기위해서 추상화하고 일반화시키고 싶을수 있겠습니다.
이 어텐션 매커니즘의 개념들로부터 시작해서 이전에 이미지 캡셔닝과 기계 번역에서 사용했었는데,이 개념들을 일반화하여 순환 신경망이나 다른 만든 신경망에다가 범용 목적의 계층으로서 넣어 사용할수있겠습니다.
우리가 보아온 어텐션 매커니즘을 재정립하기위한 방법은 쿼리 벡터 q와 (출력의 매 타임 스탭마다 은닉 상태 벡터로 구한)이전 어텐션을 입력으로하고, 거기다가 어텐드를 하고자하는 은닉 벡터를 구하는데 필요한 입력 백터의 컬랙션 x을 사용합니다. 또, 유사도 함수 f_att를 사용해서 쿼리 벡터와 입력 벡터로 된 데이터베이스에서 각각의 것들을 비교하게 되요.
아래의 내용이 우리가 여러번 보아온 어텐션 메커니즘의 계산 과정인데, 이 연산에서 유사도 함수 f_att로 쿼리 벡터와 각 입력 벡터 사이의 유사도 벡터들을 만들어내요. 이 값들은 정규화되지않은 유사도 스코어다보니 소프트맥스 함수를 사용해서 각 입력 벡터 x에 대한 확률 분포로 정규화 시키겠습니다. 출력은 단일 벡터 y로 입력 벡터 x들의 가중화된 선형 결합으로 구합니다.

일반화를 위한 첫번째 과정으로 유사도 함수 similarity functino을 바꿔봅시자. 이전에 만든 유사도 함수 f_att는 초기 어텐션 논문에서 사용되었던 것인데, 유사도 함수에서 사용되는 벡터들간의 점곱 dot product로 더 효율적으로 구할수 있다는것이 밝혀졌습니다.
이 방식으로 간소화 시키겠습니다. 이렇게함으로서 신경망의 유사도들을 일일이 계산하기보다는 모든 유사도를 행렬 곱의 형태로 더 효율적으로 계산 할수 있겠습니다.

조금더 자세히 들어보자면 사람들은 그냥 점 곱 연산을 사용하기보다는 유사도 스코어를 계산하는데 조정된 점곱 연산 scaled dot product라고 부르는 방법을 사용합니다.
이 방법은 쿼리 벡터 q와 입력 벡터들중 하나인 x_i로 유사도 스코어를 구할때, q와 x_i를 점곱해주고 이 결과를 sqrt(D_q)로 나누어줍니다. 여기서 D_q는 쿼리벡터의 차원이 되겠습니다.

이 연산을 하는 이유를 정리하자면 우리는 구한 유사도 스코어를 소프트맥스 함수에다가 적용시킬건데, 소프트 맥스 함수에 들어오는 입력이 너무 크다면 그라디언트 소멸 문제가 생기게 됩니다. 한번 어텐션 가중치 e_i가 다른것들보다 훨씬 크다면, 하나만 아주 큰 소프트 맥스 확률 분포가 나올것이고 모든 지점의 그라디언트가 0에 가까워지게 만들어 학습을 어렵게 할겁니다.
또 다른 문제로는 아주 고차원 벡터를 다루는 경우에 접 곱을 구하면 크기도 아주 커지게 되겠습니다. 두 벡터 a, b의 접곱을 계산하는 구체적인 예시를 보면 둘다 같은 차원 d인데, 이 두 벡터의 점 곱은 두 벡터 크기를 곱한것에다가 두 벡터 사이 각도에 대한 코사인를 곱해주면 되겠습니다.
한번 우리가 두 상수 벡터를 가지고 있다고 하고, 두 벡터 중 하나의 크기 magnitude는 그 벡터의 차원의 제곱근으로 조정시키겠습니다. 이는 우리가 아주 긴 차원의 신경망을 다룬다고할때, 아주 긴 차원 벡터를 가지고 점곱을하게될것이고, 그러면 아주 큰 값이 나오게 될것입니다.
그래서 이를 상쇄하기위해서 점곱에다가 차원의 제곱근으로 나누어주어, 점곱 결과는 차원의 크기에 따라 조정되겠습니다. 이렇게 하면 소프트맥스 함수를 통과한 후에도 더 나은 그라디언트를 가지게 됩니다.
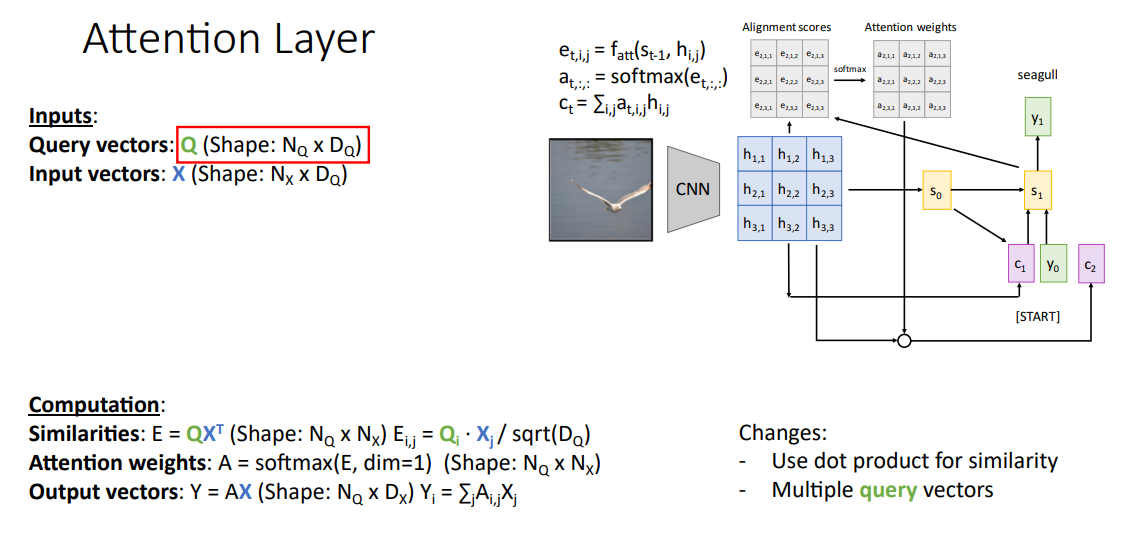
다음 일반화 방안으로 다중 쿼리 벡터를 사용하겠습니다. 지금까지 본 것들은 디코더의 각 타임 스탭마다 하나의 쿼리 벡터를 가지고 사용하였습니다. 쿼리 하나를 가지고, 입력 벡터들 전체에 대한 확률 분포를 생성하는데 사용했어요.
이제는 이 어텐션이라는 개념을 여러 쿼리 벡터의 집합을 가지고 일반화를 시켜봅시다. 입력으로 쿼리 벡터 집합 q와 입력 벡터의 집합 x를 가지고 있고, 각 쿼리벡터로 전체 입력벡터 각각에 대한 확률 분포를 생성해낸다고 합시다. 그러면 이들 끼리의 유사도를 다 계산할수 있을거에요.
우리는 각 쿼리벡터와 각 입력 벡터 사이의 유사도를 계산해야하는데, 조정된 점곱 연산으로 유사도 함수를 사용하여 단일 행렬곱 연산으로 전체 유사도 스코어들을 동시에 계산할수가 있겠습니다. 여기서 기억하고 있어야될것은 우리는 각 쿼리 벡터에대한 입력 벡터들의 확률 분포를 계산해야하는데, 출력된 어텐션 스코어의 (쿼리 벡터에 대한) 한 0차원에다가 소프트 맥스 함수를 적용시켜서 구할수가 있어요.
출력 벡터를 생성시키기 위해선, 이전에는 하나의 출력벡터를 구했지만 지금은 쿼리 벡터 집합을 가지고 하다보니 각 쿼리 벡터에 대한 각 출력을 만들어야 되겠습니다. 쿼리 q_i에 대한 출력 백터는모든 입력 백터의 가중화된 결합으로 구할수가 있는데, 여기서 쿼리벡터로 추정한 확률 분포로 가중을 주었습니다.
이러한 연산을 행렬 형태로 다룰수가 있는데, 추정한 어텐션 가중치 A와 입력 벡터들 X 사이의 하나의 행렬곱 연산으로 이 모든 선형 결합을 동시에 계산할수가 있습니다.

다음 일반화 방안은 입력 벡터를 사용하는 방법에 관한것인데, 이 슬라이드를 보면 입력 벡터들을 두가지 방향으로 사용하고 있습니다. 하나는 입력 벡터들을 각 쿼리 벡터와 함께 어텐션 가중치를 계산하는데 사용해요. 그 다음으로는 입력 벡터들을 다시 출력을 계산하는데 사용하고 있습니다.

이들은 실제로는 우리에게 필요한 서로 다른 두 함수(유사도 계산 함수와 출력 벡터 계산 함수)라고 할수 있어요. 그래서 입력 벡터를 키 벡터와 입력 벡터로 나눌수가 있는데, 우리가 하고자하는건 입력으로 그대로 쿼리 벡터 집합 q와 입력 벡터 집합 x를 가지고는 있으나, 입력 벡터들을 그대로 서로 다른 두 함수안에서 사용하는게 아니라
학습가능한 키 행렬 W_k와 학습 가능한 값 행렬 W_v를 사용해서 입력 벡터를 키 벡터의 집합과 값 벡터의 집합으로 변환 시킬수가 있겠습니다. 이제 이 두 키 벡터들과 값 벡터들을 이 어텐션 계층의 연선에서 서로 다른 두 용도로 사용하면 됩니다.
이제 우리가 할일은 유사도 스코어를 계산하는데 각각의 쿼리 벡터와 각 키 벡터를 계산하면 되고, 출력 스코어를 계산할 시에 출력들은 가중화된 값 벡터, 그러니까 값 벡터들을 추정한 유사도 스코어로 가중화한 것으로 구할수가 있겠습니다.
이걸 정리하자면 이 과정을 통해서 모델은 입력 데이터를 어떻게 사용할지 더 유연하게 고려할수 있게 됩니다. 왜냐면 쿼리 벡터는 모델에게 전달하는 내가 찾고싶다고 알려주는 것인데, 이미 알고있는것과 다른 정보를 다시 돌려받을 필요가 있어요.
이 과정은 구글에서 검색하는 과정과 비슷하다고 할 수 있는데, "how tall is the empire state building", "엠파이어 스테이트 빌딩이 얼마나 높은가요?"라는 쿼리/질문을 하면, 구글은 이 쿼리랑 수 많은 웹 패이지들을 비교하고, 여러 웹 페이지를 전달해줄거에요.
하지만 쿼리 자체는 이미 알고 있으니 우리가 쿼리랑 웹 페이지가 얼마나 잘 일치하는지 관심 가질 필요는 없고, 그보다는 찾은 데이터가 쿼리와 연관된 것인지 알고싶을 겁니다. 그래서 웹 검색 어플리케이션에서 "엠파이어 스테이스 빌딩이 얼마나 높은가요"라는 쿼리로 검색하면, 우리 원하는 데이터는 쿼리로 얻은 텍스트에 있는 몇 미터나 되는지에 대한 데이터들 일거에요.
그래서 명확하게 하자면 키 벡터와 값 벡터로 나눔으로서 모델이 입력을 두가지 방법으로 사용할수 있도록 더 유연하게 만들겠습니다.

이건 꽤 복잡한 연산인데, 이 슬라이드로 이 연산과정을 시각화 시켜 보겠습니다. 바닥에 쿼리 벡터 집합으로 q1에서 q4까지 있고, 왼편에 입력 벡터의 집합으로 x1에서 x3까지 있습니다.

첫번째로 할 일은 각 입력 벡터들을 키 행렬과 연산을하여 각 입력에 대한 키 벡터들을 만들어 냅시다.

이제 이 키 벡터를 각각의 쿼리 벡터와 비교를 하여 정규화되지 않은 유사도 스코어의 행렬을 만들수가 있어요. 이 유사도 행렬의 각 원소들은 키 벡터 하나와 쿼리 벡터 하나 사이의 조정된 점곱 연산한 값이 되겠습니다.

다음으로 할 일은 이 어텐션 스코어는 정규화되지 않았다보니 각 쿼리 벡터에 대해서 확률 분포로 만들어내겠습니다. 소프트 멕스 연산을 이 배정 행렬 E의 수직 차원으로 수행함으로서, 배정 스코어 A를 구하였습니다. 여기서 소프트 맥스 함수를 수직 방향으로 하다보니 배정 행렬의 각 컬럼은 입력 x1, x2, x3에대한 확률 분포가 되겠습니다.

다음으로 할일은 지금까지 배정 스코어를 구하는 과정을 거쳤고, 이제 출력을 계산하기 위해서는 입력 벡터들을 값 벡터로 변환을 시켜야 합니다. 각 입력 벡터를 보라색 상자의 값 벡터 v1, v2, v3으로 만들겠습니다.

그러고나서는 배정 스코어를 이용하여 값 벡터들을 가중화 선형 결합을 하겠습니다. 예를 들자면 V1을 행방향으로도 곱하고, 열방향으로도 곱하고 합 연산을 합니다. 이 말을 정리하자면 V1은 A11과 곱하고, V2는 A12와 곱하고, V3은 A13과 곱한뒤 합을하여 위로보내게 됩니다.
각 값 벡터들은 해당하는 열 값과 곱하고, 이들을 합을 해서 올림으로서 각 쿼리벡터 q에 대한 출력 벡터 y를 만들어내게 됩니다. 이러한 출력 벡터 y는 가중화된 값 벡터들의 선형 결합니고, 가중의 정도는 키 벡터와 쿼리 벡터 사이의 점곱으로 계산하였습니다.
이게 어텐션 레이어이고, 신경망에 삽입할수 있는 가장 일반적인 형태가 되겠습니다. 이건 우리가 두 데이터셋을 가진 경우, 하나는 쿼리로 보고, 다른 하나는 입력으로 보면, 이 어텐션 계층에 입력으로 사용하여 쿼리와 입력간의 결합 함으로서 계산할 수 있겠습니다.
'번역 > 컴퓨터비전딥러닝' 카테고리의 다른 글
| 딥러닝비전 13. 어텐션 - 5. 셀프 어텐션을 이용한 CNN과 시퀀스 처리 방법들 (0) | 2021.03.22 |
|---|---|
| 딥러닝비전 13. 어텐션 - 4. 셀프 어텐션 (0) | 2021.03.19 |
| 딥러닝비전 13. 어텐션 - 2. RNN과 어텐션을 이용한 이미지 캡셔닝 (0) | 2021.03.18 |
| 딥러닝비전 13. 어텐션 - 1. sequence to sequence with attention (0) | 2021.03.17 |
| 딥러닝비전 12. 순환 신경망 - 6. LSTM (0) | 2021.03.15 |