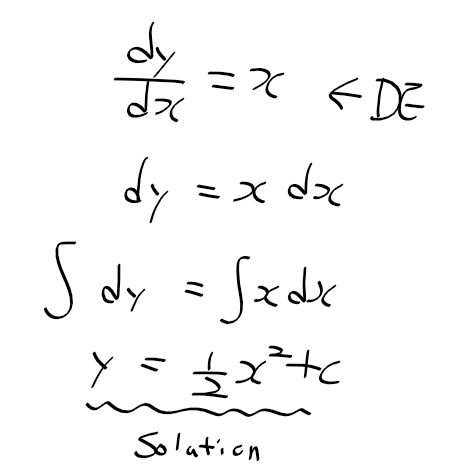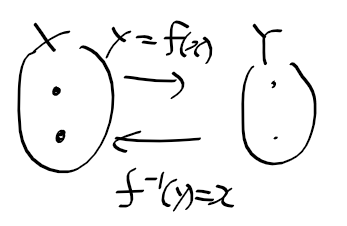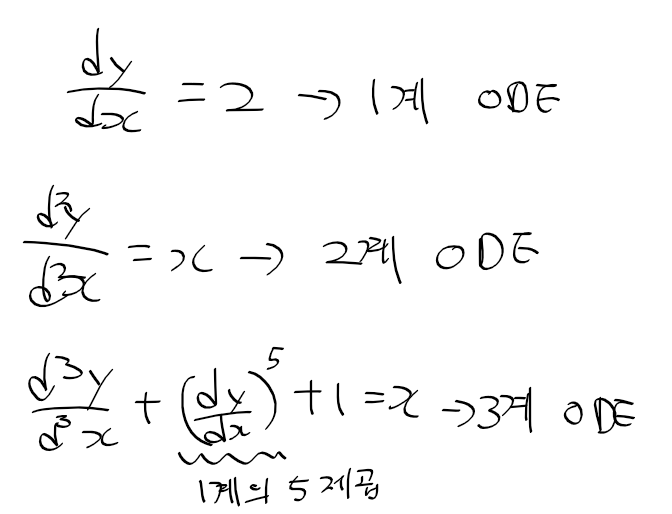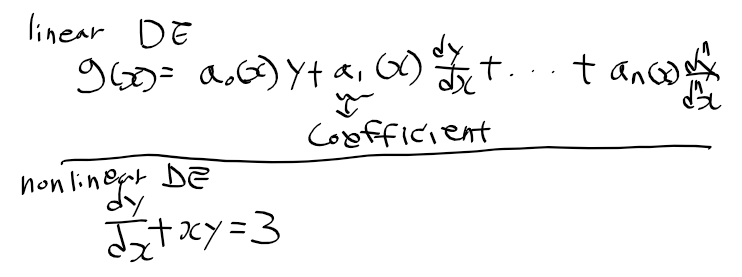집밖은 위험해

n차 동차 선형 미분방정식 n-th order homogeneous linear defferential equation

기본 해 집합 fundamental set of solution

- 위 식에서 1차 독립인 해 y_1, . . ., y_n을 원소로 갖는 집합을 기본 해 집합이라 함.

일반 해 general solution

- 다음의 식이 일반해가 됨

n차 비동차 선형미분방정식 n-th order nonhomogeneous linear defferential equation

- 아래의 식과 같이 g(x)가 0이 아닌 미분방정식

비동차 선형 미분방정식의 특수해와 동차해

- 특수해 particular solution : 비동차 선형미분방정식을 만족하고, 임의의 상수를 포함하지 않는 함수 y_p

- 동차해 homogeneous solution : g(x) = 0으로 할때 동차 선형미분방정식의 일반해 y_h

비동차 선형 미분방정식의 일반해

1차 결합, 선형 결합 linear combination

선형 독립 linear independent과 선형 종속 linear dependent

- 구간 I의 모든 x에 대해 다음의 선형 결합이 주어 질때 

1차 선형 미분 방정식 first order linear differential equation

- 아래와 같이 선형성을 가진 1차 미분방정식을 선형 미분 방정식이라 한다.

전미분 total differential

- 1변수 함수의 경우

- 2변수 함수의 경우

=> 모든 변수들의 변화율과 미소 증분 곱들의 합

완전 미분 exact differential

- F_1(x, y), F_2(x, y)가 연속일때 다음을 만족하는 함수가 존재하면 F_1dx + F_2dy는 완전 미분

변수 분리 Seperation of Variables

- 미분방정식의 변수 분리를 통한 해를 구하는 방법으로 양 변에 적분을 하여 구함

대응 관계에 따른 함수의 종류

- 다대일 대응 : 여러개의 독립변수 x가 하나의 종속 변수 y에 대응

- 일대다 대응 : 하나의 독립변수가 여러개의 종속변수 y에 대응

- 일대일 대응 one to one corresponding function : 하나의 x가 하나의 y에 대응

역함수 inverse function

- 기존의 함수가 독립 변수 x에 대한 y를 구한다면, 역함수는 y를 독립변수로 줄때 x를 얻을수 있는 함수

초기값 문제 Initial Value Proble IVP

- 초기값이 주어질때 얻을수 있는 미분방정식의 해 -> 특수해

초기값 문제에서 해의 존재성, 유일성

- 해의 존재성 : 초기값 문제에서 최소 하나의 해를 가지는 경우

- 유일성 : 존재하는 해가 하나인 경우

미분 방정식의 해

- 독립 변수의 x와 종속 변수 y의 미분 방정식을 만족하는 함수 y

- 양의 해와 음의 해/일반해와 특수해/ 특이해

양의 해와 음의 해

- y = f(x) 형태의 양함수인 해를 양의 해 explicit solution

- f(x, y) = 0 형태의 음함수인 해를 음의 해 implicit solution

일반해와 특수해

- 일반해 general solution : 미분 방정식을 만족하는 함수가 여러개 일 수 있으며 이 해가 일반 해

- 특수해 particular solution : 일반해에 초기조건이 주어질때 얻을수 있는 해

특이해 singular solution

- 일반해로 표현할 수 없는 해

- 미분방정식을 만족하지만 일반해에는 포함되지 않는 해

 이전부터 평균 제곱법, 최소 평균 제곱 같은 개념이 많이 사용되고 중요한건 알고 있었다.

그런데 이러한 개념들을 뭐라고 하는지 한마디로 어떻게 정의해야하는지 잘 모르겟더라

그러다가 최근 전체적인 개념 정리를하고 SLAM 공부를하면서

내가 궁금했던 이런 용어들이 최적화 관련 개념인것 같아 보였다.

그래서 잠깐 최적화 이론을 공부하려고 했으나 너무 벅찼고

최적화를 배우기 앞서 무엇을 해야할까 고민하다

수치해석을 봐야 할것 같더라

그런데 이 수치해석이라는 과목이

미분 방정식에 수치적인 방법을 적용하여 해를 구하는 이론인걸 이제서야 알게 됬는데

미분 방정식을 주로 다루는 과목이 공업수학이니 공부하게 되었다.

공과 분야를 나왔는데 왜 공업수학을 잘 모르는지

변명아닌 변명을 하자면

대학원 다닐때도 대부분의 사람들이 공업 수학이란 용어 자체를 쓰질 않았고

나보고 공업수학에 대해서 공부하라는 사람이 없었다.

그러다 보니 공업수학이란 과목이 있는지 그렇게 중요한 과목인지도 잘 몰랐었다.

그래서 지금 공업 수학을 훑어보고 있는데

공업 수학이라는 과목을 한번도 안본 채로

제어공학을 배우고, 영상처리, 딥러닝을 공부한 내가 미쳤구나 싶더라

이런 응용 과목들에서 동차해, 특수해, 일반해, 특이해, 선형성, 분해같은

공업 수학에서 배우는 용어들이 수차례 나오지만

응용 분야 관련 서적에서 나오는 공업 수학 관련 용어 설명이 빈약하고

잘 정리되어있다 해도 이해하기 힘들어

억지로 외우거나 간단하게 보고 넘어갔지 이런 내용들의 전후 배경이나 맥락같은건 전혀 몰랐다.

그러다보니 지금까지 해에 대한 개념과 방정식들의 성질, 종류 조차 정확하게 모르고 있었다.

좋게 생각하면 응용 분야에서 몇번 본 개념들이 있으니까

공업수학을 볼때 내가 필요한 부분과 필요 없는 부분이 보이긴 한다.

만약 응용 분야보다 공업 수학을 먼저 공부했다면

공업 수학 전체를 보겠다고 삽질하느라 포기했을지도 모른다.

그런데 진작에 공업수학을 공부한 뒤 이런 분야들을 공부 했으면 훨씬 수월하게 했을텐데 아쉬움이 크다.

 안그래도 SLAM 전반에 대해서 공부하고

경로 계힉 알고리즘을 공부해야지 생각하다가 벽을 느낀 지금

뭘 공부해야할까 막막한 와중에

수치 해석과 공업 수학을 만나면서

한동안 좋은 학습 목표를 찾은것 같아 뿌듯하기도 하다

최근 SLAM 마무리를 하면서 잠깐 풀어지기는 했는데

다시 이 과목들을 간단간단히 훑어보면서 조금씩 속도를 올려야되겠다.

상미분 방정식

- 종속 변수에 대한 독립변수의 상 미분을 가진 방정식

계수에 따른 분류

- 미분 방정식의 최대 계수에 따라 분류

선형성에 따른 분류

- 선형 미분 방정식 linear differential equation : 선형성을 가진 미분 방정식

- 비선형 미분 방정식 nonlinear differential equationi : 선형성을 갖지 않는 미분 방정식

동차성에 따른 분류

- 종속 변수 y나 y의 도함수를 가진 항의 유무에 따라 구분

- g(x) : y나 y의 도함수를 가진 항

- 동차 미분 방정식 homogeneous differential equation : g(x) = 0

- 비동차 미분방정식 nonhomogeneous differential equation : g(x) != 0