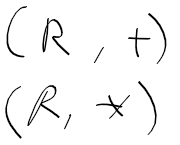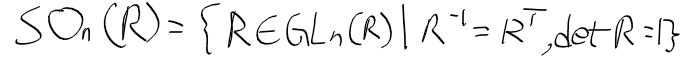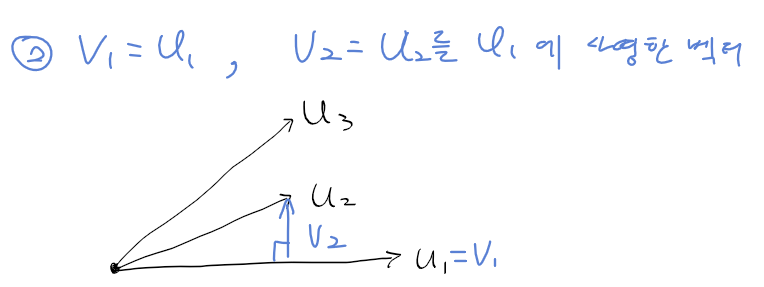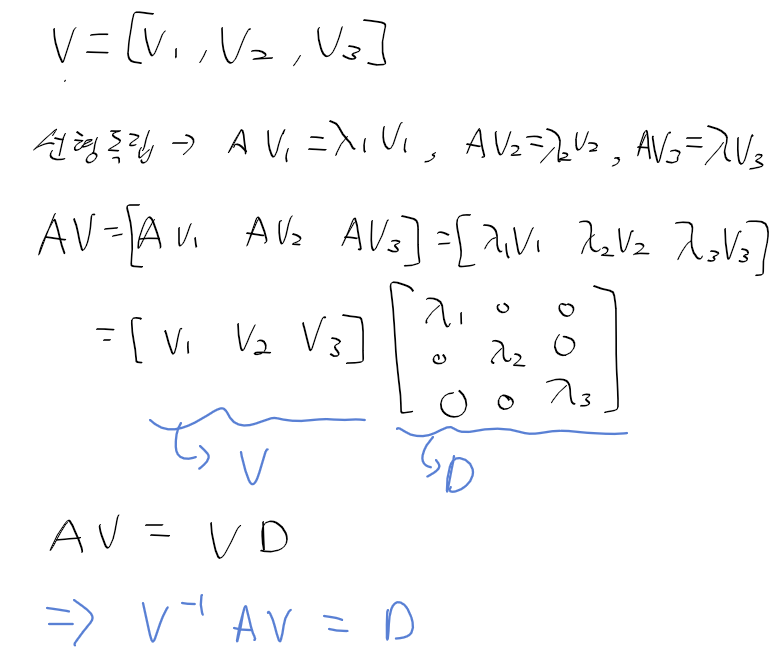다변수 함수 multi variable function
- 독립 변수가 한개인 일변수 함수와 달리 독립 변수가 여러개 존재하는 함수
함수
- 하나 또는 여러개의 정의역 원소 (독립변수)가 하나의 공역 원소(종속변수)에 대응하는 관계
이차 형식 quadratic form
- 중간에 행렬과 앞 뒤로 두 벡터의 곱으로 이루어진 함수 형태

- 3변수, ..., n 변수 함수도 이차 형식으로 표현 가능

다변수 함수의 의미
- 다변수 함수는 보통 다음의 형태가 됨.

편미분 partial deriavative
- 1변수에서의 미분인 상미분과는 달리, 다변수 함수에서 한 변수에 대한 부분(partial)적인 미분이라 할 수 있다.

전미분 total derivative
- 함수의 모든 변수에 대한 편미분과 미소 증분의 곱들의 합
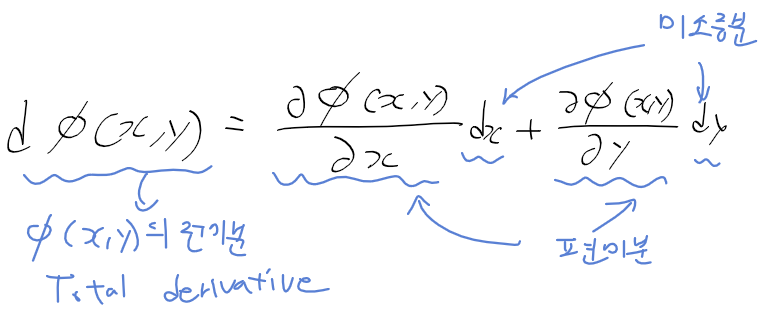
'수학 > 선형대수, 최적화' 카테고리의 다른 글
| 최적화 - 5. 헤시안 행렬 (0) | 2020.07.21 |
|---|---|
| 최적화 - 4. 그라디언트와 자코비안 (0) | 2020.07.21 |
| 최적화 - 2. 1 변수 함수 (0) | 2020.07.20 |
| 선형대수 - 12. 회전 (0) | 2020.07.18 |
| 선형대수 - 11. 군과 직교 행렬 (0) | 2020.07.16 |