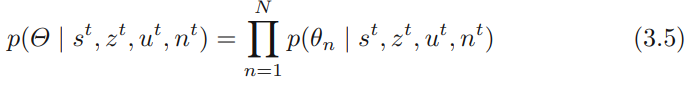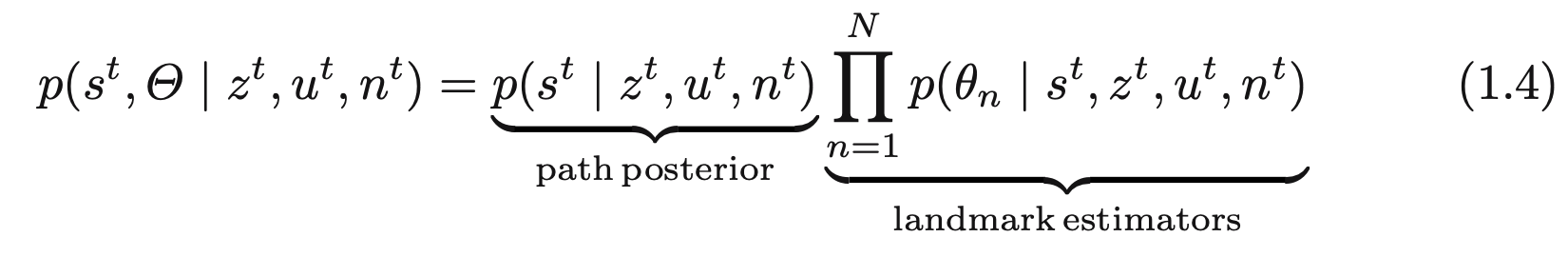집밖은 위험해

3.3 FastSLAM 1.0 알고리즘

 식 (3.3)과 같은 사후확률 분해는 SLAM 문제에 있어서 중요한 구조를 보여주고 있습니다. 이 구조는 적절한 조건이 주어짐에 따라 랜드마크들사이에 상관관계가 존재하지않음을 알려주고 있습니다. FastSLAM은 M + 1개의 필터를 사용하여 분해된 표현을 사용하고 있으며, 모든 N + 1개들은 저차원이 됩니다.

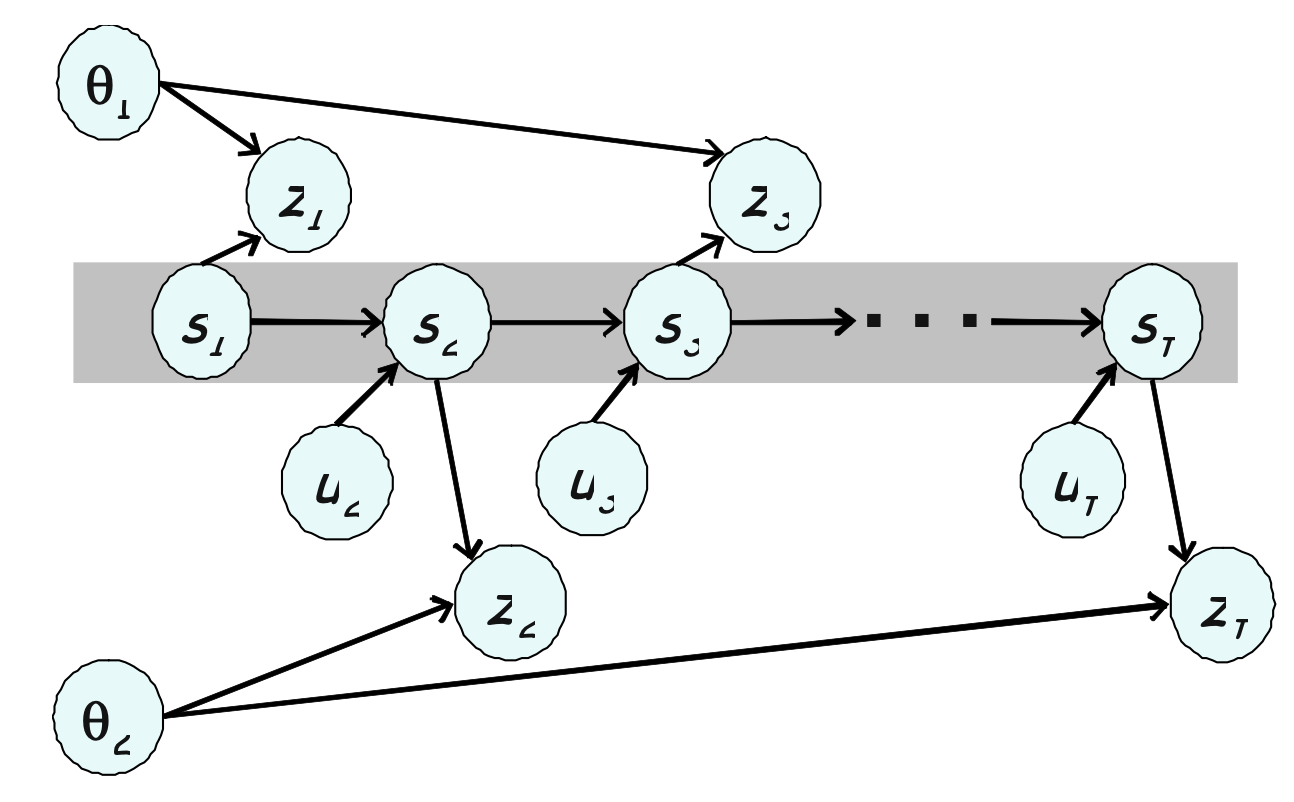
 FastSLAM은 식 (3.3)의 첫번째 항인 로봇의 경로 사후확률을 파티클 필터를 사용하여 추정합니다. 나머지 N개의 조건부 랜드마크 사후확률은 EKF를 사용하여 추정됩니다. 각 EKF 추적기는 단일 랜드마크의 위치를 추적하며, 그러므로 고정된 크기의 저차원이 됩니다. 이 랜드마크 EKF는 파티클필터에서의 파티클이며, EKF에서 처리되는 파티클인 로봇의 경로에 조건부가 됩니다.

그림 3.3 파티클 필터에서의 M개의 파티클이 있으며, 각 파티클은 N개의 독립적인 EKF들을 가지고 있습니다. 랜드마크 추정치들 사이에 아무런 상관관계를 갖지 않습니다.

 총 N * M 개의 EKF가 존재하며, M개는 파티클필터에서 전체 파티클의 개수이고, 파티클 필터는 그림 3.3에서 시각적으로 보여주고 있습니다. 각 FastSLAM의 파티클들은 다음의 형태를 띄고 있습니다.

 꺽쇄 표기인 [m]은 파티클의 인덱스를 나타내며 $s^{t, [m]}$은 m번째 파티클의 경로 추정, $\mu_{n, t}^{[m]}$, $\Sigma_{n, t}^{[m]}$은 경로 $s^{t, [m]}$가 주어질때 n번째 특징의 위치를 나타내는 가우시안의 평균과 공분산이 됩니다.

 이 값들은 모두 m번째 파티클 $S_{t}^{[m]}$에 속하며, FastSLAM 사후확률에는 총 M개가 있습니다. 시간 t-1로부터 시간 t에 대한 사후확률을 계산하는 필터링은 $S_{t-1}$에서 새 파티클 집합인 $S_{t}$를 생성하는 과정도 포함됩니다. 새로운 파티클 집합은 최신 제어 입력 $u_t$와 관측 $z_t$(그리고 대응관계 데이터 연관 $n_t$)를 반영합니다.

 여기서 갱신 과정은 4가지 단계로 수행됩니다. 첫번째로 새로운 로봇의 자세가 최신 제어 입력을 반영하여 각 파티클로 그려집니다. 각 자세들은 적절한 로봇 경로 추정기 $s^{t-1, [m]}$에 추가됩니다. 다음으로 관측된 랜드마크에 대응하는 랜드마크 EKF들이 새로운 관측으로 갱신됩니다. 로봇의 경로 파티크이 실제 경로 사후확률로부터 그려지지 않았기 때문에 각 파티클들은 이 차이를 반영하기위해 중요도 가중치를 받습니다. 새로운 파티클 집합 $S_t$가 중요도 리샘플링을 사용하여 가중화된 파티클 집합으로부터 생성됩니다. 이 중요도 리셈플링 단계는 파티클들이 실제 사후확률을 따라 분포되도록 하기위해 필수적입니다. 이 FastSLAM의 기본적인 4가지 단계는 표 3.1에서 보여주고 있으며, 아래의 섹션에서 자세히 살펴보겠습니다.

표 3.1 기본 FastSLAM 알고리즘 개요

3. FastSLAM 1.0

 이번 장에서는 파티클 필터를 사용하는 SLAM 방법인 FastSLAM 기본 알고리즘을 살펴보겠습니다.

 FastSLAM 알고리즘은 EKF가 실패하게 되는 SLAM 문제의 구조적인 성질에 기반하는 것으로, 로봇에 의해 얻은 각 제어 입력과 관측은 적은 수의 상태변수만을 제약하게 됩니다. 제어는 로봇의 이전 자세에 상대적인 현재 로봇의 자세로 제한하며, 관측은 로봇에 상대적인 랜드마크의 위치를 제한합니다. 많은 수의 확률적 제약들이 반영이 된 후에서야 지도는 완전 상관관계를 가지게 됩니다. EKF는 상태 변수에서 어느 구조적인 가정을 가지지 않아 이 희소성으로인한 이점을 가지지 못하게 됩니다.

 FastsSLAM은 조건부 독립을 사용하는데, 이는 사후 확률을 저차원 추정 문제로 분해하여 SLAM 문제에서 구조적인 희소성의 결과가라고 할수 있습니다. 이 알고리즘의 결과로 큰 맵을 효율적으로 스케일 조정할수 있고, 데이터 연관에있어서 애매한 경우에도 강인해 질 수 있습니다.

3.1 파티클 필터링

 칼만 필터와 확장 칼만필터는 파라미터 모델(다변수 가우시안)으로 확률 분포를 나타냅니다. 하지만 파티클 필터는 유한개의 상태 샘플들의 집합을 사용하여 분포를 나타내는데, 이 상태 샘플들을 파티클이라고 합니다. 높음 확률을 가진 영역은 높은 밀도의 파티클들을 가지고 확률이 낮은 공간에는 적은 수의 파티클을 가지게 됩니다. 충분한 수의 샘플들이 주어짐으로서, 이 비모수적인 방법은 재멋대로이며 복잡한 다중 모달 분포를 근사화 할수 있겠습니다.

 샘플의 수를 제한하여 실제 분포는 쉽게 복원될수 있겠습니다. 이 표현을 이용해서 베이즈 필더 갱신 식은 간단한 샘플링 과정을 사용하여 구현할수 있습니다.

 파티클 필터는 현실 세게에서 다양한 추정 문제에 성공적으로 적용되어 왔습니다. 가장 흔한 피티클 필터링의 예시중 하나는 몬테카를로 위치추적 MCL인데, MCL에서 파티클의 집합은 고정된 지도상에 상대적인 로봇의 가능한 자세들에대한 분포를 나타냅니다.

 그림 3.1이 이 예시를 보여주고 있는데, 그림 3.1 a는 로봇은 자세에 대한 정보가 주어지지 않으므로 불확실성은 파티클들을 균일 분포를 따르도록 맵 전반에 뿌려 보여주고 있습니다. 그림 3.1 b는 여러 제어와 관측이 반영된 후의 파티클 필터를 보여주고 있습니다. 여기서 사후 확률은 근사화되는 단봉 분포로 모여들고 있습니다.

 멀티 모달 신뢰도를 추적하고, 비선형 동작, 관측모델을 사용하는 능력은 파티클 필터가 더욱 강인하게 수행하게 만들어 줍니다. 하지만 최악의 경우에 주어진 신뢰도를 추적하는데 필요한 파티클의 수가 상태 공간의 차원에 따라 지수적으로 증가할수도 있습니다. 그래서 표준 파티클 필터링 알고리즘은 상대적으로 저차원의 문제에서만 사용 가능합니다. 파티클 필터는 특히 수백만 차원으로 이루어진 SLAM 문제에서는 부적합합니다.

 하지만 앞으로 볼 파트에서 어떻게 SLAM이 로봇 경로 추정치가 주어질때 독립된 랜드마크 추정의 문제들로 분해하는지 살펴보겠습니다. 로봇 경로 사후확률은 저차원이며 파티클 필터로 쉽게 추정할수 있으며 FastSLAM이라고 부르는 결과 알고리즘은 Rao-Blackwellized 파티클 필터의 하나의 예시라고 할수 있겠습니다.

3.2 분해된 사후확률 표현법

 대다수의 SLAM 방법들은 지도와 로봇 자세에 대한 사후확률 추정에 기반하고 있습니다.

 FastSLAM은 약간 다른 양을 계산하는데, 지도와 로봇의 경로가 주어질때에 대한 사후확률을 계산하여야 합니다.

 이런 미묘한 차이는 SLAM 사후확률을 단순한 항들의 곱으로 분해할수 있게 도와줍니다. 그림 3.2는 동적 베이즈 네트워크 DBN으로 SLAM 문제를 해석한 것을 보여주고 이씃ㅂ니다. DBN에서 묘사된 시나리오에서 로봇은 시간 t=1일때 랜드마크 $\theta_1$를 관측하고, 시간 t=2일떄 $\theta_2$를 관측합니다. 시간 t=3에서는 랜드마크 $\theta_1$을 제관측하고 있습니다. 여기서 회색 영역은 로봇의 경로를 보여주고 있습니다. 이 다이어그램으로부터 SLAM문제에서 중요한 조건부 독립들을 볼수 있습니다.

 특히 만약 로봇의 진짜 경로를 안다면, 랜드마크 $\theta_1$의 위치는 랜드마크 $\theta_2$에 조건부 독립이 됩니다. 이러한 DBN의 터미놀로지를 사용하여 로봇의 경로는 두 랜드마크 노드 $\theta_1$과 $\theta_2$를 나눌수 있게 됩니다.

이 조건부 독립은 매우 중요한 결과를 만드는데, 로봇의 경로에 대한 정보가 주어지면 한 랜드마크에 대한 관측은 다른 랜드마크의 위치에 대한 아무런 정보를 주지않는다는 것입니다. 다시말하면, 한 장애물이 로봇의 진짜 경로를 알려준다면, 모든 랜드마크의 위치를 독립적인 양으로서 추정할수 있습니다. 이는 사후확률 (3.2)가 단순한 항들의 곱으로 분해할수 있음을 의미합니다.

 이 분해는 머피가 처음 개발하였으며, 거기서 SLAM 사후확률이 로봇 경로 사후확률과 로봇의 경로가 주어질때 N개의 랜드마크 사후확률의 곱으로 분해할수 있게 됩니다. 이 분해는 매우 중요하며, SLAM 문제의 구조로부터 구할수 있습니다.

3.2.1 FastSLAM 분해 증명

 FastSLAM 분해는 SLAM 경로 사후확률 (3.2)로부터 얻을수 있습니다. 조건부 확률 정의를 사용하여 SLAM 사후확률을 다음과 같이 다시 정리할 수 있습니다.

 그래서 분해된 사후확률 (3.3)을 구하기 위해서, 다음과 정리하기만 하면 충분하겠습니다.

2.6 강인한 데이터 연관

 실제 SLAM 응용에서, 데이터 연관 $n^t$를 관측할수 있는 경우는 매우 드뭅니다. 하지만 랜드마크 자세의 불확실성이 랜드마크 사이의 거리 평균보다 상대적으로 작다면,  올바른 데이터 연관을 결정하기 위해 휴리스틱한 방법을 사용하는것이 효율적일수 있겠습니다. 특히 SLAM에서 데이터 연관을 하기위한 가장 흔한 방법은 최대 우도를 이용하여 각각의 관측치에 대해 지정해주는것으로, 다른말로 하자면 각 관측은 가장 가능성있는 랜드마크에 배정이 되는것입니다. 만약 최대 확률이 고정 임계치보다 작다면, 이 관측은 새로운 랜드마크로 판단합니다.

 EKF에서의 경우 관측 $z_t$와 기대 관측 $\hat{z_{n_t}}$사이의 차이에 대한 함수로 이 관측 확률을 표현하며, 이 차이를 개변 innvation이라고 부릅니다.

  이 휴리스틱한 데이터 연관은 음의 로그 우도를 사용하여 공식을 정리하기도 하는데 다음과 같습니다.

 이 식에서 두번째 항은 마할라 노비스라고 하는 거리로, 랜드마크의 추정치와 관측 공분산으로 정규화된 거리라고 할수 있습니다. 이런 거리를 사용한 데이터 연관은 종종 최근접 이웃 nearest neighbor 데이터 연관이나 최근접 이웃 gating이라고도 합니다.

 최대 우도 데이터 연관은 올바른 데이터 연관이 잘못된 데이터 연관보다 많이 수행될때 잘 동작되며, 하지만 랜드마크의 자세 불확실도가 크다면 여러개의 데이터 연관이 높은 확률을 가지게 될것입니다. 그래서 잘못된 데이터 연관이 골라진다면, 이 결정은 지도 작성 정확도을 크게 떨어트릴 수 있습니다. 이러한 데이터 연관 모호성은 로봇 센서의 노이즈가 심하다면 쉽게 발생할 수 있습니다.

 이 문제에 대응하기 위한 한 방법은 애매하지않은 데이터 연관을 할수 있는 다른 관측치를 반영하는 방법이 있겠습니다. 하지만 SLAM을 수행하는 환경이 노이즈가 심하다면 많은 관측치들이 제대로 수행되지 못하게 됩니다. 그래서 관측치 반영이 실패하는것은 미래의 데이터 연관이 더 큰 모호함을 가지도록하는 과추정된 랜드마크 공분산을 만들수 있겠습니다. 그래서 데이터 연관에 있어서 노이즈가 심한 환경에서도 애매함에 대처할 수 있도록 많은 복잡한 방법들이 개발되었습니다.

2.6.1 지역 지도 시퀀싱 

 타르도스는 초음파 데이터를 사용하여 내부 환경의 지도들을 작성하는 지역 지도 시퀀싱이라 부른는 방법을 개발하였습니다. 소나 센서들은 매우 노이즈가 심하고, 보는 지점에 의존적인 경향이 큽니다. 지역 지도 시퀀싱 알고리즘은 로봇이 짧은 거리를 이동하는 동안 많은 초음파 측정치들을 모아, 이 측정치들은 로봇 주위에 대한 전체 관측치들로부터 코너와 선 세그먼트들을 감지하는 두개의 허프 변환에 사용됩니다.

 허프 변환으로부터 얻은 특징들이 로봇의 지역 환경 지도를 만드는데 사용되고, 여러개의 지역 지도가 모여 전체 전역 지도를 만들게 됩니다.

 허프 변환은 데이터 연관을 강인하게 만들어 주는데, 다중 센서 관측치들이 서로다른 로봇의 자세로부터 취득되고 데이터의 올바른 결정을 하도록 하기 때문입니다. 이러한 방법을 사용하여 노이즈가 큰 센서로도 적은 비용으로 정확한 지도를 얻을수 있었습니다. 저자는 또한 RANSAC알고리즘을 노이즈 센서를 이용한 데이터 연관 결정시에 다른 투표 알고리즘으로도 소개하였습니다.

2.6.4 Iterative Closet Point

 스캔 매칭은 Iterative Closet Point ICP 알고리즘의 수정된 버전에 기반한 데이터 연관 방법입니다. 이 알고리즘은 데이터 사이 상관관계들이 식별되는 단계와 현재 대응관계로부터 새로운 로봇의 경로를 복원하는 단계 사이를 대체하는 알고리즘으로, 이 반복 최적화는 기대값 최대화 Expectation Maximization EM과 RANSAC과 비슷하다고 할수 있겠습니다.

 우선 지역적으로 일관된 지도가 스캔 매칭과 최대 우도 지도작성 방법으로 생성됩니다. 다음으로 이동 전후로 구한 다른 센서 스캔사이의 관측치들을 매치 시킵니다. 추정상의 대응관계에 기반하의 로봇 자세의 새로운 집합을 구할수 있게 됩니다. 이 대안적인 방법은 컨버전스 기준에 도달할때까지 여러번 반복 됩니다. 이 과정은 매우 넓은 공간에서의 데이터 연관에 있어서 효과적으로 사용됩니다.

2.6.5 다가정 추적

 모든 데이터 연관 알고리즘은 단일 데이터 연관 과정을 선택하여 EKF나 EKF 근사 알고리즘에 반영됩니다. 여기서 시간에 따라 다중 데이터 연관 가정들을 유지시키는 몇가지 알고리즘이 있습니다. 이들은 단일 측정으로부터 올바른 데이터 연관을 추론할수 없다면 특히 유용합니다. 이러한 방법중 하나가 다중 가정 추적 Multiple Hypothesis Tracking으로 MHT 알고리즘이라고 부릅니다. MHT는 다중 타겟을 추정하는 가정들의 집합들을 사용합니다.

 특정 관측이 여러 값과 유요한 데이터 연관 해석 s를 가진다면, 새로운 가정들이 각 가정에 따라 생성됩니다. 제한하지 않고 늘어나는 가정의 수를 유지하기 위해서, 가능성이 낮은 가정들을 제거하기 위해 휴리스틱한 방법들이 사용됩니다.

 SLAM 문제에서 여러개의 EKF 가정들을 유지하는것은 많이 사용되지 않는데, 각 EKF가 로봇의 자세와 전체 지도에 대한 신뢰도를 유지하기 때문입니다. 네봇은 데이터 연관이 애매할때 지도 작성을 중지하고, 이 애매함이 해결될떄까지 파티클 필터를 사용하여 다가정 위치 추정을 수행하는 비슷한 기술을 개발하였습니다.

 지도 작성은 데이터 연관이 애매한 경우 잘 수행될수 없으므로, 로봇 자세에 대한 다중 가정들은 작은 차원수를 가질 것입니다. 하지만 이방법은 데이터 연관 애매함이 우발적으로 발생하는 경우에만 잘 동작합니다. 이것은 루프가 폐쇠될 때 우발적인 데이터 연관 문제에 있어서 효과적이나, 이 알고리즘은 애매함이 지속된다면 지도작성을 수행하지 않게 됩니다.

2.7 FastSLAM과 현존하는 기술들과의 비교

 이 자료에선 SLAM 사후확률을 추정하는 대안 방법인 FastSLAM에 대해 소개하겠습니다. SLAM 문제를 공간적으로 분해하는 하부지도 EKF 방법과는 달리 FastSLAM은 시간에 따라 변화하는 SLAM 사후확률을 로봇의 경로에 대해 분해합니다. 그 결과 지도에 존재하는 랜드마크 수에 따라 로그적으로 변하게 되고, 수백만개의 특징이 존재하는 지도에서도 효율적으로 수행될수 있습니다.

 FastSLAM은 EKF같은 모수화된 분포를 사용하는 데신 잠재적인 로봇 경로에서 샘플링을 수행하는데 이를 통해 FastSLAM이 SLAM 사후확률을 나타내는 다른 데이터 연관 과정들을 적용할수 잇게 되었습니다. 그러므로 이 알고리즘은 MHT와 하이브리드 필터 방법의 다중 가정 추적 능력을 가지게 되고, 데이터 연관 애매함이 크고 일관되더라도 위치 추정과 지도작성을 수행할수 있습니다.

2.5 조절하는 SLAM 알고리즘 scaling slam algorithms

2.5.1 하부지도 방법 submap methods

 칼만 필터는 선형 가우시안 슬램 문제에서 최적의 해를 찾을수 있으나 큰 지도의 경우 계산하기 어렵습니다. 그래서 SLAM 연구에서는 더 큰 환경에서 EKF를 사용가능한 SLAM 알고리즘을 개발하기 위한 연구가 진행되었습니다. EKF의 계산 복잡도는 상태 변수들 사이 쌍 상관간계를 나타내는 공분산 행렬로 부터 비롯되었는데, 하나의 랜드마크 관측을 반영하기 위해서 다른 모든 상태 변수들까지 영향을 주게 되었습니다.

 일반적으로 하나의 랜드마크 관측은 다른 거리가 먼 랜드마크의 위치에 별 영향을 주지 않습니다. 이런 이유로 많은 연구자들이 전역 지도를 작은 하부지도로 분해하는 EKF 기반 SLAM 알고리즘을 개발하였습니다. 이러한 방법들 중 하나는 로봇이 전역 지도의 일부 공간에 특징 시간 간격동안 남아있다는 사실을 이용하였는데, 연기와 압축 확장 칼만 필터 둘다 로봇이 득정 하부지도에 존재하는 동안에 지역정보를 전역 지도에 반영하는것을 미루는 기술입니다. 이러한 기술들은 완전 EKF로서 동일한 최적의 결과를 구할수 있습니다. 하지만 두 알고리즘 다 계산이 상수로 줄어들었는데, 전체 지도 갱신 수행이 덜 자주 수행되기 때문입니다.

 전역 지도를 여러개의 하부지도로 나누는 것은 지도 요소들 사이에 상과노간계를 더 희소하게 만드는데, 희소성의 증가로 센서 갱신을 효율적으로 계산할수 있게 되었습니다. 네트워크 동조 특징 지도나 ATLAS, 지역 지도작성 알고리즘, 그리고 비동조화 확률적 지도작성 프레임워크 등 모두 하부지도의 희소 네트워크 사이의 관계들을 고려한것이 됩니다.

 로봇이 하나의 하부지도 밖으로 나갈때 새로운 하부지도를 만들거나 이전에 정의한 하부지도로 이동하는것이 됩니다. 이러한 벙법들은 데이터 연관이 주어지는 경우에 상수 시간을 필요로 하는 관측 반영 요구 계산량을 줄입니다. 하지만 이런 계산적인 이득은 전반적인 속도를 다소 늦출수 있습니다. 각 하부지도는 전체 지도의것보다 더 적은 특징들을 가지고, 멀리 있는 랜드마크의 관측의 영향으로 여러 상관관계 링크에 반영됤 ㅜ있겠습니다.

 귀반트와 네봇은 하부최적 SLAM이라고 하는 비슷한 방법을 소개하였는데, 지역 지도들은 적은 수의 기반 랜드마크으로 계산됩니다. 서로 다른 랜드마크들의 무리들이 다른 좌표계상에서 유지되기 띠문에, 이들은 모든 랜드마크가 단일 좌표계에 있을때 보다 더 쉽게 분해될수 있습니다. 이 알고리즘의 결과로 실제에 가까운 추정치를 구할 수 있으나 선형 시관과 메모리만을 필요로 합니다.

2.5.2 희소 확정 정보 필터 sparse extended information filters

 SLAM 문제를 분해하는 다른 필터 방법으로 지도를 마르코브 랜덤 필드와 비슷한 이웃한 랜드마크 끼리 사이의 잠재 함수를 사용하여 지도를 나타내는 방법이 있습니다. 그러한 방법 중 하나로 희소 확장 정보 필터 Sparse Extended Information Filter SEIF가 제안되었는데, SEIF는 칼만 필터의 다른 파리미터 표현법인 정보 필터를 구현한 것입니다. 공분산 행렬 $\Sigma$로 계산하는 데신 SEIF는 정밀 행렬인 $\Sigma^{-1}$을 갱신시킵니다. 이 파라미터화는 가까운 랜드마크 끼리 상관관계를 유지시킨다면 정밀 행렬이 희소하기 때문에 유용합니다. 적절한 추정을 통해 이 기술들은 데이터 연관이 주어지는 경우 선형 메모리 공간으로 효율적으로 갱신이 가능합니다.

2.5.5 그래프 최적화 방법

 오프라인 슬램 알고리즘 군 중에 SLAM 문제를 최적화 문제로 다루는 방법이 있습니다. 이러한 기술은 이전 쳅터에서 살펴본 독립을 사용하는데, 모든 이전의 자세들을 유지함으로서, 희소 링크의 집합으로 SLAM 사후확률에서 다른 변수들 사이 제약의 집합을 표현할 수 있습니다. 기존의 최적화 기술을 사용하는 이러한 링크들은 가장 가능성있는 지도와 최적의 로봇 경로를 찾을수 있도록 해줍니다. 이 파라다임을 가장 먼저 사용한 사람은 루와 밀리오스로, 구트만이 처음 구현하였습니다. Golfarelli et al은 SLAM 문제와 질량 스프링 모델사이 관계를 정리하였고, Duckett el at은 그러한 문제를 효율적으로 푸는 기술들을 제시하였습니다. folkesson과 christensen은 관련된 그래프 완화 방법들과 함꼐 그래프 SLAM이란 용어를 처음 소개하였습니다. 그래프 기반 최적화 방법들은 오프라인에서 주로 사용됩니다.

2.3 마르코브 체인으로 SLAM

 SLAM 문제는 확률 마르코브 체인으로 가장 잘 표현할수 있겠습니다. 마르코브 체인 그림은 아래의 그림 2.2에서 볼수 있겠습니다. 현재 로봇의 자세 $s_t$는 이전 시간에서의 로봇 자세 $s_{t-1}$과 제어 $u_t$에 대한 확률 함수로 쓸수 있으며, 어떻게 제어가 로봇의 동작을 수행하는지 보여주므로 이 함수를 동작 모델이라 합니다. 게다가, 동작 모델은 제어 입력의 노이즈가 얼마나 로봇의 자세 추정치에 불확실도를 주는지또한 나타냅니다. 이 동작 모델은 아래와 같이 표기하겠습니다.

 로봇이 획득한 센서 관측치 또한 확률적인 함수로 나타낼수 있는데 이를 관측 모델이라고 합니다. 관측 $z_t$는 관측된 랜드마크 $\theta_{n_t}$아 로봇의 자세 $s_t$에 대한 함수이며, 관측 모델은 로봇의 센서에 대한 물리와 에러 모델을 나타냅니다. 이 관측모델은 다음과 같이 표기하겠습니다.

 동작 모델과 관측 모델을 사용하여 시간 t에대한 SLAM 사후확률을 시간 t - 1의 사후확률을 이용하여 재귀적으로 계산 할 수 있습니다. 이

재귀적은 갱신 규칙을 베이즈 필터라고 하며, 대부분이 온라인 SLAM알고리즘의 기초가 됩니다.

2.3.1 베이즈 필터 정리

 베이즈 필터는 다음의 SLAM 사후확률로부터 구할수 있게습니다. 우선 (2.6)의 사후확률을 베이즈 정리에 따라 다음과 같이 고칠 수 있겠습니다.

 베이즈 정리로부터 분자는 정규화 상수로, $\eta$로 표기합니다. 다음으로 $z_t$는 로봇의 자세 $s_t$와 지도 $\Theta$, 그리고 최신 데이터 연관 $n_t$에 대한 함수란 점을 따라, 이 사후확률은 다음과 같이 됩니다.

  이제 식 (2.10)의 우항을 시간 t-1에서 로봇의 자세에 대한 조건부가 되도록 전체 확률 법칙을 사용하겠습니다.

 적분 안에있는 좌항은 조건부 확률 정의 사용하여 전개하겠습니다.

 이제 적분 내부에 존재하는 첫번째 항은 이전에 보았던 동작 모델처럼 자세 $s_{t-1}$과 $u_t$가 주어질 때 자세 $s_t$로 간소화 시킬수가 있게 됩니다.

 이제 적분 안에있는 우항 2개를 합칠수가 있고,

 현재 자세 $u_t$와 데이터 연관 $n_t$는 최신 관측 $z_t$없이, $s_{t-1}$이나 $\Theta$에 대한 아무런 정보를 주지 못하므로, 적분 안에 있는 시간 t에 대한 요소들은 버릴수가 있겠습니다.

 이렇게 하여 시간 t-1에서의 SLAM 사후확률과 동작 모델 p($s_t$ | $s_{t-1}$, $u_t$), 관측 모델 p($z_t$ | $s_t$, $\Theta$, $n_t$)가 주어질때, 시간 t에서 SLAM 사후확률을 계산하는 재귀식을 정리하였습니다.

2.4. 확장 칼만 필터

 일반적으로 식 (2.15)의 재귀 갱신에서 적분은 닫힌 형식으로 계산될수 없습니다. 하지만 SLAM 사후확률과 동작 모델, 관측 모델의 형태를 제한함으로서 근사화하는 SLAM 알고리즘들이 개발되었습니다.

* 닫힌 형식 closed form과 열린 형식 open form

 많은 SLAM 알고리즘들은 SLAM 사후확률을 추정하기위해 확장칼만필터 사용을 제안한 스미스와 치즈먼의 논문에서 시작되었습니다.

 EKF는 SLAM 사후확률을 고차원, 다변수 가우시안으로 나타내는데, 여기서 평균 $\mu_t$, 공분산 $\Sigma_t$가 됩니다. 여기서 평균은 로봇과 랜드마크의 가장 높은 확률의 상태이며, 공분산은 모든 상태변수들 쌍 사이에 존재하는 상관관계들을 나타내고 있습니다.

 평면을 이동하는 로봇의 경우 평균 벡터 $\mu_t$는 2N + 3의 차원을 가지며 여기서 N은 랜드마크의 갯수가 됩니다. 나머지 3차원은 로봇의 자세를 나타내는것이고, 2개의 차원은 각 랜드마크의 위치를 명시하기 위해 필요합니다. 이처럼 공분산 행렬은 (2N + 3) x (2N + 3)의 크기를 가지게 됩니다. 그래서 EKF 사후확률을 계산하기 필요한 사후확률의 수는 지도에 존재하는 랜드마크의 수에 이차적이게 됩니다.

 그림 2.3은 1차원 공간에서 단일 랜드마크의 위치를 추정하는 칼만 필터의 간단한 예시가 되겠습니다. 그림 2.3(a)는 랜드마크의 현재 신뢰도(실선)과 노이즈를 포함된 새로운 랜드마크 관측(점선)을 보여주고 있습니다. 칼만 필터는 선형 시스템에서 가우시안 신뢰도를 사용한 최적해를 구하는데, 이 경우에서 점선으로 그려진 관측을 반영한 후에 얻은 새로운 사후확률이 그림 2.3에서 두꺼운 선으로 보여주고 있습니다.

 기본 칼만필터 알고리즘은 가우시안 노이즈를 가지는 선형시스탬에서 최적의 추정치를 찾습니다. 이름 대로 확장 칼만 필터는 기본 칼만 필터 알고리즘을 비선형 시스템에서 사용하도록 확장시킨 것입니다. 이 확장 칼만 필터는 동작과 관측 모델을 비선형 모델로 대체하여 수행하며, 여기서 비선형 모델은 시스템의 특정 지점에서 선형화를 수행하여 나타냅니다. 일반적으로 확장 칼만 필터를 통한 추정치는 실제 모델이 선형에 가깝고, 필터의 시간 간격이 작다면 좋은 성능을 보입니다.

 동작 모델은 비선형 함수 h($x_{t-1}$, $u_t$)와 선형화된 노이즈 공분산 $P_t$로 나타낼수 있습니다. 이와 마찬가지로 관측 모델은 비선형 함수 g($x_t$, $n_t$)와 선형화된 노이즈 공분산 $R_t$로 나타낼수 있습니다. 확장칼만필터 갱신식은 아래와 같습니다.

 실제 환경에서 SLAM을 할때 선형인 경우는 매우 드뭅니다. 그래서 확장 칼만 필터로 보통 좋은 결과를 구할 수 있습니다. 그래서 EKF를 온라인 슬램 알고리즘의 표준이라고 부르기도 합니다.

2.2 SLAM 사후확률

 시간 t에서의 로봇의 자세를 $s_t$라고 하겠습니다. 평면 공간에서 로봇이 주행하면서, 로봇의 자세는 평면 공간에서의 x-y 위치와 해딩각도로 이루어 집니다. 앞으로 살펴볼 모든 실험은 평면 환경에서 수행될 것이나, 어떤 알고리즘들은 3차원 세계에서 다루겠습니다. 로봇의 모든 시간에서의 자세로 이루어진 로봇의 완전한 궤적은 $s^t$라고 쓰며 아래와 같습니다.

 이번에는 로봇의 주위 환경을 N개의 점 랜드마크의 집합으로 설계할수 있습니다. 점 랜드마크는 센서로부터 추출한 특징의 위치로, 레이저 스캔으로 구한 기하학적 특징이나 카메라로 얻은 시각 특징 같은게 될수 있습니다. N개의 랜드마크 위치 집합을 {$\theta_1$, . . ., $\theta_N$}이라고 쓰겠습니다. 전체 지도에 대해서 간단하게 적으면 $\Theta$로 표기하겠습니다.

 로봇은 주위 환경에서 주행하면서, 로봇의 동작에 대해 상대적인 정보들을 수집하는데, 이 정보는 로봇의 바퀴에 장착된 오도미터나, 관성 센서로 구할수 있으며, 아니면 로봇이 수행하는 제어입력으로 구할수 있겠습니다. 원점이 어디인지든 간에 로봇의 동작을 제어 입력이라고 부릅니다. 시간 t에 대한 제어 입력을 $u_t$라 하며, 모든 제어 입력의 집합을 $u^t$라고 표기합니다.

 로봇이 주행하는 동안에 근처에 있는 랜드마크들을 관측도 하는데, 평면 공간에서의 SLAM 문제에서 로봇들은 장애물, 랜드마크에 대한 거리와 방위를 측정하게 됩니다. 이 시간 t에서의 관측을 $z_t$라 하며, 로봇이 수집한 모든 관측 집합을 $z^t$라고 표기합니다.

 SLAM에 있어서 센서 관측치들은 개별적인 랜드마크에 대한 정보로 분할하여 다룰수 있는데, 각 랜드마크 관측치는 다른 간측치로부터 독립적으로 반영할수 있습니다. 이는 성공적으로 SLAM을 구한하기 위해서 가공되지 않은 센서 데이터로부터 랜드마크 특징들을 하나 하나 추출하는데 있어, 현실적인 가정이라 할 수 있겠습니다. 그래서 각각의 관측은 로봇의 현재 자세 $s_t$에 대해 상대적인 랜드마크의 위치 $\theta_n$에 대한 정보를 전달한다고 할수 있겠습니다. 

 여기서 변수 n은 관측된 랜드마크의 아이디로, 현실에서는 많은 수의 랜드마크들이 비슷비슷하게 생겨서, 랜드마크의 아이디는 관측할수 없습니다. 관측 $z_t$로 얻은 랜드마크의 아이디를 $n_t$라고 표기하겠습니다.($n_t$ $\in$ {1, . . .N}). 예를들어 $n_8$ = 3이라고 한다면, 시간 t=8에 로봇이 관측한것이 3번째 랜드마크라는 의미가 되겠스빈다. 랜드마크 아이디를 보통 데이터 연관 data associations이나 대응관계 correspondences라고 부릅니다. 이러한 모든 데이터 연관 집합을 $n^t$로 표기합니다.

 쉽게 보자면, 로봇은 매 시간마다 제어입력 $u_t$를 수행하고, 관측 $z_t$를 얻는다고 할수 있겠습니다. 시간 t에서 다중 관측치또한 처리될수 있겠으나 조금 복잡한 표기를 해야되겠습니다.

 위의 정의들을 사용하여 SLAM의 주요 목표는 노이즈를 가진 관측치들 $z^t$와 제어 입력들 $u^t$이 주어질때, 로봇의 자세 $s_t$와 지도 $\Theta$의 최고의 추정치를 구하는것이라 할수 있겟습니다.

 확률적인 용어로 이는 아래의 사후확률로 표현할 수 있겠고,

 모든 데이터 연관에 대한 집합 $n^t$가 주어진다면, 이 사후확률은 다음과 같이 고칠수 있겠습니다.

 이번에는 동시적 위치 추정 및 지도 작성 Simultaneous Localization and Mapping SLAM에대한 개요를 살펴볼 것이고,

우선 확장 칼만 필터에 기반한 알고리즘에 대해서 소개하겠습니다.

2.1 문제 정의

 이동 로봇이 모르는, 정적 환경에서 주행중이라고 생각해봅시다. 로봇은 제어 입력들을 수행하고, 주위 환경에 대해 관측을 하게 될 것입니다. 제어와 관측은 둘다 노이즈로 훼손되는데, SLAM은 이런 노이즈를 가진 제어입력과 관측치 집합으로부터 로봇의 경로와 주위 지도를 생성하는 처리과정이라 할수 있겠습니다.

 로봇의 경로를 알고있다면, 지도 작성은 간단한 문제가 되어 주위 환경에 존재하는 물체의 위치를 독립적인 필터로 추정할수 있을 겁니다.

하지만 로봇의 경로를 알지 못할때 로봇의 경로에서 존재하는 에러가 지도 상에 존재하는 랜드마크의 위치 오차에 영향을 주게되므로 로봇과 지도의 상태는 동시적으로 추정되어야만 합니다.

 로봇의 자세 에러와 지도 에러 사이 상관관계는 그림 2.1(a)의 그래프에서 볼수있겠습니다. 로봇은 점선 경로를 따라 이동하면서, 주위에 원으로 그려진 랜드마크들을 관측할 것입니다. 여기서 그림자 타원은 시간 변화에 따른 로봇의 자세에 대한 불확실성을 보여주고 있습니다. 제어 에러로 인해 로봇의 자세는 로봇이 움직일 수록 더 큰 불확실성을 가지게 됩니다. 랜드마크 자세의 추정치는 그림자없는 타원으로 나타나고 있는데, 로봇의 자세가 불확실해지기 때문에 관측된 랜드마크 위치 추정치의 불확실성 또한 증가하게 됩니다.

  그림 2.1 (b)에서는 로봇은 루프를 닫고, 이전에 관측한 랜드마크를 재방문하였습니다. 첫번쨰 랜드마크의 위치를 높은 정확도로 알고있기 때문에, 로봇의 자세 추정치의 불확실성은 크게 줄어들게 됩니다. 로봇 자세에 대한 이러한 새로운 정보의 발견으로 이전 로봇 자세에 대한 확실도 또한 파악할수 있게 됩니다. 이를 통해 로봇이 이전에 관찰했던 랜드마크들의 불확실성 또한 줄어듭니다.

 이 글을 보는 분들은 그림 2.1 (b)에서 루프 폐쇄전에 그림자 타원이 줄어들지 않는것을 알 수 있는데, 이는 로봇의 자세 불확실성을 보여주고 로봇의 이전 자세 추정치가 수정되지 않았기 때문입니다.

 루프 주위에 있는 모든 랜드마크를 관측한 영향들은 SLAM 문제에서 상관성의 결과라고 할수 있겠습니다. 지도에서의 오차는 로봇의 경로에서의 오차와 관련되고, 로봇의 자세에 대한 정보를 알려주는 관측이 이전에 관측한 모든 랜드마크에 대한 정보들 또한 전달하게 됩니다.

(a) 루프 폐쇠전 : 로봇 자세 불확실성이 커짐에 따라 랜드마크의 불확실성또한 증가하고 있습니다. 시간 변화에 따른 로봇의 자세 추정치는 그림자 타원이며, 랜드마크 추정치는 그림자없는 타원이 보여주고 있습니다.

(b) 루프 폐쇄후 : 이미 알고있는 랜드마크를 다시 방문하는것으로 로봇의 자세 불확실성을 낮춰주고, 이전에 관측된 랜드마크의 불확실성 또한 줄여줍니다.

그림 2.1 로봇 동작 에러와 지도 에러의 상관관계

FastSLAM 알고리즘

 Fast SLAM은 표 1.1처럼 4단계로 주어진 제어와 관측치를 이용해 파티클 필터를 재귀적으로 갱신 합니다.

첫 번째 단계는 이전 자세와 새 입력을 이용하여 각 파티클에 대한 로봇의 세로운 자새를 구합니다.

다음으로, 최근 관측치와 함께 각 파티클에서의 랜드마크 필터는 표준 EKF 갱신 식을 사용하여 갱신 됩니다.

각 파티클에는 중요도 가중치를 할당하고, 이 가중치에 따라 새로운 샘플들을 생성합니다.

중요도를 이용한 리샘플링 단계를 통해 제안 분포와 사후 확률 분포 사이의 차이를 갱신하여 줍시다.

 이 갱신 과정은 샘플의 수가 무한에 가까울수록 실제 사후확률 분포에 가까워 지지만

실제로는, FastSLAM 사용시에 상대적으로 적은 파티클 (M = 100)만 하더라도 좋은 사후확률을 구할수가 있겠습니다.

 로봇의 경로를 사용하여 슬램 사후확률을 분해하는것은 경로의 길이가 시간에 따라 커지므로 좋지 않은 선택처럼 보일수 있으며, 로봇의 경로에 대한 사후확률 추정시 필터의 차원이 시간에 따라 더 증가할거라고 볼수도 있습니다.

 하지만  FastSLAM에서는 그렇지 않은데,

랜드마크 갱신 식과 중요도 가중치는 최신 로봇의 자세에만 의존하므로

이전의 로봇 경로에 대한것을 잃어버려도 상관없기 때문입니다.

 그 결과 FastSLAM의 각 파티클들은 현재 로봇의 자세에 대한 추정치만 유지하면 되고, 파티클 필터의 차원수가 시간이 지나더라도 고정되어 집니다.

1.6.1 로그 복잡도

 FastSLAM은 EKF보다 두가지 주요한 장점을 가지고 있습니다.

첫째로, 지도에 대한 추정을 분해하여 로봇의 경로가 주어질때 각 랜드마크 사후확률을 추정하는것으로 함으로써

FastSLAM은 효율적으로 완전 슬램 사후확률을 계산할수 있게 됩니다.

 동작 갱신과 관측 갱신, 그리고 중요도 가중치 계산은 모두 파티클 하나당 상수 시간에 수행할 수 있게 됩니다.

리샘플링 단계는 순수한 FastSLAM으로 구현한다면, 선형 시간에서 수행될 수 있지만

 로그 시간을 수행하도록 구현할수도 있는데,

랜드마크 추정기를 배열 대신 이진 트리의 형태로 각 파티클들을 구성하면 됩니다.

1.6.2 다중 가정 데이터 연관

 로봇 경로에 대한 샘플링은 올바른 데이터 연관을 수행하는데 중요한 영향을 줍니다.

FastSLAM에서 각 파티클은 특정한 로봇의 궤적을 나타내기 때문에,

각각의 파티클에 대해 동일한 정보 연관이 수행될 필요는 없습니다.

 FastSLAM에서 데이터 연관 결정은 각 파티클에 기반하여 만들어 지는데,

올바르게 정보 연관을 하는 파티클은 높은 가중치를 받을 것이고, 이후 리샘플링 될 확률이 더 커질것입니다.

 하지만 잘못된 데이터 연관을 수행한 파티클은 적은 가중치를 받을것이고, 이후 사라질것입니다.

데이터 연관으로 샘플링을 하는것으로 FastSLAM이 새로운 증거가 생길때, 이전의 데이터 연관을 고칠수 있게 해줍니다.

 이 과정은 랜드마크의 추가나 제거시에도 동일하게 수행됩니다.

종종, 각 파티클의 데이터 연관은 파티클들이 랜드마크의 갯수가 다른 지도를 만드는 상황을 만들기도 합니다.

 이로 인해 가장 높은 확률의 지도를 계산하기 어렵게 만드나,

FastSLAM이 더 확실한 근거가 쌓일때 잘못된 랜드마크를 제거할수 있도록 해줍니다. 

 어느 관측치가 특정 파티클에서 새로운 랜드마크를 생성시켜버리나

다른 관측치들은 이 관측이 이미 존재하는 랜드마크에 속한다고 판단한 경우에

새로운 랜드마크를 생성해야한다는 파티클은 적은 가중치를 가지게 될 것이고,

이후 리샘플링 단계에서 올바르지 않은 파티클이 사라지면서 이전에 생성된 랜드마크도 제거될것입니다.

1.7 개요

 이 자료를통해 FastSLAM 알고리즘의 전반에 대해서 살펴볼것이고,

다양한 시뮬레이션과 실제 환경에서 얻은 데이터 셋으로 FastSLAM과 EKF의 성능을 비교해보겠습니다.

 2장에서 SLAM문제를 공식화하고, EKF 기반 선행 방법들에 대해 주로 다루어보겠습니다.

 3장에서 데이터 연관이 주어지거나 주어지지 않은 경우 둘다에 대해 가장 간단한 버전의 FastSLAM도 살펴봅시다.

FastSLAM 1.0이라고 하는 버전은 구현하기 가장 간단한 FastSLAM 알고리즘으로, 일반적인 SLAM 환경에서도 잘 동작합니다.

 4장에서는 기존의 FastSLAM의 개선된 버전인 FastSLAM 2.0을 볼것인데, 기존의 것보다 더 좋은 결과를 보여줍니다.

이 알고리즘은 현재 관측을 파티클의 제안 분포에 반영하여, 결과적으로 동작 노이즈가 센서 관측보다 큰 경우에 더 정확한 결과를 계산할수 있게 만들어 줍니다.

 5장에서는 SLAM 문제와 같은 구조인 동적 물체 추적 문제를 살펴볼 것이고, 어떻게 FastSLAM 알고리즘의 바리에이션을 이용하여 정밀하게 위치 추정되지 않은 로봇으로 부터 동적인 물체를 추적하는지 살펴보겠습니다. 

1.6 FastSLAM

실제 로봇의 주행 궤적과 랜드마크 사이의 관계 

 1.2 결합 추정에서 지도의 요소들 사이 상관관계는 로봇의 자세 불확실성에서 발생하는것을 봤었습니다.

그래서 실제 로봇의 주행 궤적을 안다면 랜드마크 위치들을 독립적으로 추정할수 있겠습니다.

로봇의 실제 궤적을 아는것으로 랜드마크 위치 추정은 조건부 독립이 된다고 할 수 있습니다.

 이 내용에 대한 증거로 아래의 그림 1.5와 같이 동적 베이지안 네트워크로 슬램 문제를 보면 확인 할 수 있습니다.

 시간 t에 대한 로봇의 자세를 $s_t$로 이 자세는 이전의 로봇 자세 $s_{t-1}$과 제어 $u_t$를 실행하여 얻을 수 있습니다.

시간 t에 대한 관측은 $z_t$로 표기하며 로봇의 자세 $s_t$와 관측된 랜드마크 $\theta_{n_t}$로 얻을 수 있습니다.

 위 그림의 시나리오 데로 따라가면 랜드마크 1은 t = 1, 3일때 관측되며, 랜드마크 2은 t=2에서 관측됩니다.

회색 공간은 로봇의 전체 경로를 강조하고 있습니다.

 이 네트워크를 보면 알수 있지만 이 경로는 두개의 랜드마크를 나타내는 노드로 나누어지게 됩니다.

정리하면 로봇의 실제 주행 경로를 알고 있는 상태에 첫번째 랜드마크의 위치를 안다고 해서

두번쨰 랜드마크의 위치를 구하는데 도움되지 않는다고 할수 있습니다.

랜드마크간 조건부 독립을 이용한 SLAM 사후확률 분해

 이 관계를 통해서, 데이터 연관이 주어질때 SLAM 사후확률은 다음의 곱 형태로 구할수 있겠습니다.

 이 분해를 통해 완전 SLAM 사후확률이 N + 1개의 재귀 추정기로 나눌수 있음을 알수 있으며,  1개 추정기는 로봇의 경로에 대한 것이고,

N개의 로봇의 경로 추정에 조건부이며, 서로의 랜드마크 위치에독립적인 추정기들로 이루어집니다.

 위 분해된 사후확률은 파티클 필터를 이용하여 효과적으로 근사화 할수 있으며, 이 파티클 필터의 파티클들은 로봇의 샘플 경로가 됩니다.

여기서 각 파티클들은 N개의 독립 랜드마크 추정기에 붙여져(EKF로 구현됨), 해당 랜드마크에 대한 로봇의 자세가 되겠습니다.

 랜드마크 필터들이 각각의 랜드마크의 자세를 추정하므로, 각 필터는 저차원이 되겠습니다.

그래서 전체적으로 N x M개의 칼만 필터가 사용됩니다.

이 파티클 필터를 갱신하는 알고리즘을 FastSLAM이라 부르겠습니다.

 통계학에 친숙한 사람이라면 이 FastSLAM이 Rao-Blackwellized Prticle Filter를 구현한 것임을 알수 있을 겁니다.

관측과 제어 사이 제약

 주어진 시간에 대해 누적된 관측과 제어들은 상태 변수들의 일부 부분집합을 제약하며,

데이터와 상태 변수 간에 의존관계에서 이러한 희소성은 슬램 사후확률 계산을 더 효율적으로 하도록 사용할수 있습니다.

상관관계와 부분 지도

 예를들어 서로 멀리 떨어진 두 랜드마크는 약한 상관 관계를 가지며,

다른 멀리 떨어진 랜드마크 쌍 또한 비슷하게 약한 상관관계를 가지게 됩니다.

많은 EKF SLAM 알고리즘은 이러한 성질을 사용하여 전체 지도를 작은 부분집합 지도로 나누어 사용합니다.

EKF 분해

 큰 EKF를 많은 수의 느슨하게 결합된 작은 EKF로 나눌수 있겠습니다.

이 방법은 EKF 근사 알고리즘이 선형 시간에 수행되고,

관측 반영이 상수 시간에 수행될수 있도록 하는 장점을 가지고 있습니다.

 슬램 문제를 희소하도록 분해함으로서 효율적인 EKF 기반 알고리즘을 만들수 있고,

이 새 알고리즘은 기존의 EKF 처럼 데이터 연관시 동일한 어려움을 직면하게 됩니다.

데이터 연관 개선 방안

 앞으로 상태 변수들 간에 의존관계에서 희소성을 이용하여 이 문제를 개선한 방법을 볼것이고,

슬램 사후확률 계산을 효율적으로 할수 있도록 이 방법은 다중 데이터 연관 가정을 사용하겠습니다.

이를 통해 큰 데이터 연관 애매함을 가진 넓은 환경에서도 사용가능한 슬램 알고리즘을 얻을 수 있습니다.