2.3 마르코브 체인으로 SLAM
SLAM 문제는 확률 마르코브 체인으로 가장 잘 표현할수 있겠습니다. 마르코브 체인 그림은 아래의 그림 2.2에서 볼수 있겠습니다. 현재 로봇의 자세 $s_t$는 이전 시간에서의 로봇 자세 $s_{t-1}$과 제어 $u_t$에 대한 확률 함수로 쓸수 있으며, 어떻게 제어가 로봇의 동작을 수행하는지 보여주므로 이 함수를 동작 모델이라 합니다. 게다가, 동작 모델은 제어 입력의 노이즈가 얼마나 로봇의 자세 추정치에 불확실도를 주는지또한 나타냅니다. 이 동작 모델은 아래와 같이 표기하겠습니다.

로봇이 획득한 센서 관측치 또한 확률적인 함수로 나타낼수 있는데 이를 관측 모델이라고 합니다. 관측 $z_t$는 관측된 랜드마크 $\theta_{n_t}$아 로봇의 자세 $s_t$에 대한 함수이며, 관측 모델은 로봇의 센서에 대한 물리와 에러 모델을 나타냅니다. 이 관측모델은 다음과 같이 표기하겠습니다.

동작 모델과 관측 모델을 사용하여 시간 t에대한 SLAM 사후확률을 시간 t - 1의 사후확률을 이용하여 재귀적으로 계산 할 수 있습니다. 이
재귀적은 갱신 규칙을 베이즈 필터라고 하며, 대부분이 온라인 SLAM알고리즘의 기초가 됩니다.

2.3.1 베이즈 필터 정리
베이즈 필터는 다음의 SLAM 사후확률로부터 구할수 있게습니다. 우선 (2.6)의 사후확률을 베이즈 정리에 따라 다음과 같이 고칠 수 있겠습니다.

베이즈 정리로부터 분자는 정규화 상수로, $\eta$로 표기합니다. 다음으로 $z_t$는 로봇의 자세 $s_t$와 지도 $\Theta$, 그리고 최신 데이터 연관 $n_t$에 대한 함수란 점을 따라, 이 사후확률은 다음과 같이 됩니다.
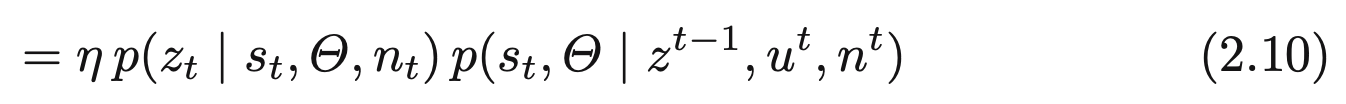
이제 식 (2.10)의 우항을 시간 t-1에서 로봇의 자세에 대한 조건부가 되도록 전체 확률 법칙을 사용하겠습니다.

적분 안에있는 좌항은 조건부 확률 정의 사용하여 전개하겠습니다.

이제 적분 내부에 존재하는 첫번째 항은 이전에 보았던 동작 모델처럼 자세 $s_{t-1}$과 $u_t$가 주어질 때 자세 $s_t$로 간소화 시킬수가 있게 됩니다.
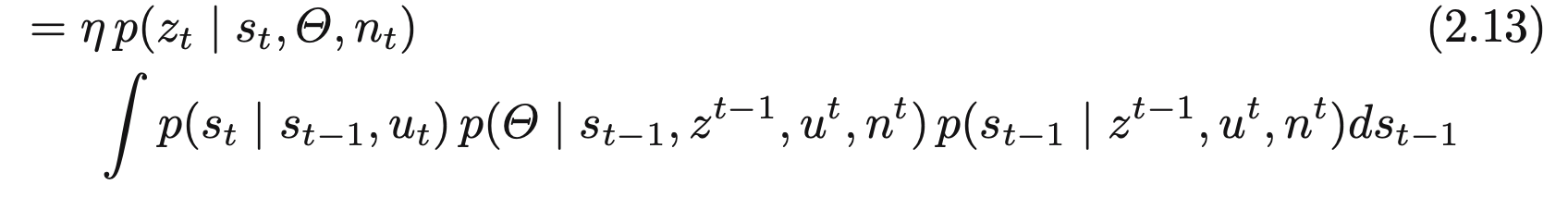
이제 적분 안에있는 우항 2개를 합칠수가 있고,

현재 자세 $u_t$와 데이터 연관 $n_t$는 최신 관측 $z_t$없이, $s_{t-1}$이나 $\Theta$에 대한 아무런 정보를 주지 못하므로, 적분 안에 있는 시간 t에 대한 요소들은 버릴수가 있겠습니다.
이렇게 하여 시간 t-1에서의 SLAM 사후확률과 동작 모델 p($s_t$ | $s_{t-1}$, $u_t$), 관측 모델 p($z_t$ | $s_t$, $\Theta$, $n_t$)가 주어질때, 시간 t에서 SLAM 사후확률을 계산하는 재귀식을 정리하였습니다.

2.4. 확장 칼만 필터
일반적으로 식 (2.15)의 재귀 갱신에서 적분은 닫힌 형식으로 계산될수 없습니다. 하지만 SLAM 사후확률과 동작 모델, 관측 모델의 형태를 제한함으로서 근사화하는 SLAM 알고리즘들이 개발되었습니다.
* 닫힌 형식 closed form과 열린 형식 open form

많은 SLAM 알고리즘들은 SLAM 사후확률을 추정하기위해 확장칼만필터 사용을 제안한 스미스와 치즈먼의 논문에서 시작되었습니다.
EKF는 SLAM 사후확률을 고차원, 다변수 가우시안으로 나타내는데, 여기서 평균 $\mu_t$, 공분산 $\Sigma_t$가 됩니다. 여기서 평균은 로봇과 랜드마크의 가장 높은 확률의 상태이며, 공분산은 모든 상태변수들 쌍 사이에 존재하는 상관관계들을 나타내고 있습니다.

평면을 이동하는 로봇의 경우 평균 벡터 $\mu_t$는 2N + 3의 차원을 가지며 여기서 N은 랜드마크의 갯수가 됩니다. 나머지 3차원은 로봇의 자세를 나타내는것이고, 2개의 차원은 각 랜드마크의 위치를 명시하기 위해 필요합니다. 이처럼 공분산 행렬은 (2N + 3) x (2N + 3)의 크기를 가지게 됩니다. 그래서 EKF 사후확률을 계산하기 필요한 사후확률의 수는 지도에 존재하는 랜드마크의 수에 이차적이게 됩니다.

그림 2.3은 1차원 공간에서 단일 랜드마크의 위치를 추정하는 칼만 필터의 간단한 예시가 되겠습니다. 그림 2.3(a)는 랜드마크의 현재 신뢰도(실선)과 노이즈를 포함된 새로운 랜드마크 관측(점선)을 보여주고 있습니다. 칼만 필터는 선형 시스템에서 가우시안 신뢰도를 사용한 최적해를 구하는데, 이 경우에서 점선으로 그려진 관측을 반영한 후에 얻은 새로운 사후확률이 그림 2.3에서 두꺼운 선으로 보여주고 있습니다.

기본 칼만필터 알고리즘은 가우시안 노이즈를 가지는 선형시스탬에서 최적의 추정치를 찾습니다. 이름 대로 확장 칼만 필터는 기본 칼만 필터 알고리즘을 비선형 시스템에서 사용하도록 확장시킨 것입니다. 이 확장 칼만 필터는 동작과 관측 모델을 비선형 모델로 대체하여 수행하며, 여기서 비선형 모델은 시스템의 특정 지점에서 선형화를 수행하여 나타냅니다. 일반적으로 확장 칼만 필터를 통한 추정치는 실제 모델이 선형에 가깝고, 필터의 시간 간격이 작다면 좋은 성능을 보입니다.
동작 모델은 비선형 함수 h($x_{t-1}$, $u_t$)와 선형화된 노이즈 공분산 $P_t$로 나타낼수 있습니다. 이와 마찬가지로 관측 모델은 비선형 함수 g($x_t$, $n_t$)와 선형화된 노이즈 공분산 $R_t$로 나타낼수 있습니다. 확장칼만필터 갱신식은 아래와 같습니다.

실제 환경에서 SLAM을 할때 선형인 경우는 매우 드뭅니다. 그래서 확장 칼만 필터로 보통 좋은 결과를 구할 수 있습니다. 그래서 EKF를 온라인 슬램 알고리즘의 표준이라고 부르기도 합니다.
'로봇 > SLAM' 카테고리의 다른 글
| FastSLAM - 2.6 강인한 데이터 연관 (0) | 2020.07.07 |
|---|---|
| FastSLAM - 2.5 조절하는 SLAM 알고리즘 (0) | 2020.07.07 |
| FastSLAM - 2.2 SLAM 사후확률 (0) | 2020.07.07 |
| FastSLAM - 2. SLAM 문제 (0) | 2020.07.07 |
| FastSLAM - 1.6 FastSLAM+ (0) | 2020.07.07 |