1.6 FastSLAM
실제 로봇의 주행 궤적과 랜드마크 사이의 관계
1.2 결합 추정에서 지도의 요소들 사이 상관관계는 로봇의 자세 불확실성에서 발생하는것을 봤었습니다.
그래서 실제 로봇의 주행 궤적을 안다면 랜드마크 위치들을 독립적으로 추정할수 있겠습니다.
로봇의 실제 궤적을 아는것으로 랜드마크 위치 추정은 조건부 독립이 된다고 할 수 있습니다.
이 내용에 대한 증거로 아래의 그림 1.5와 같이 동적 베이지안 네트워크로 슬램 문제를 보면 확인 할 수 있습니다.
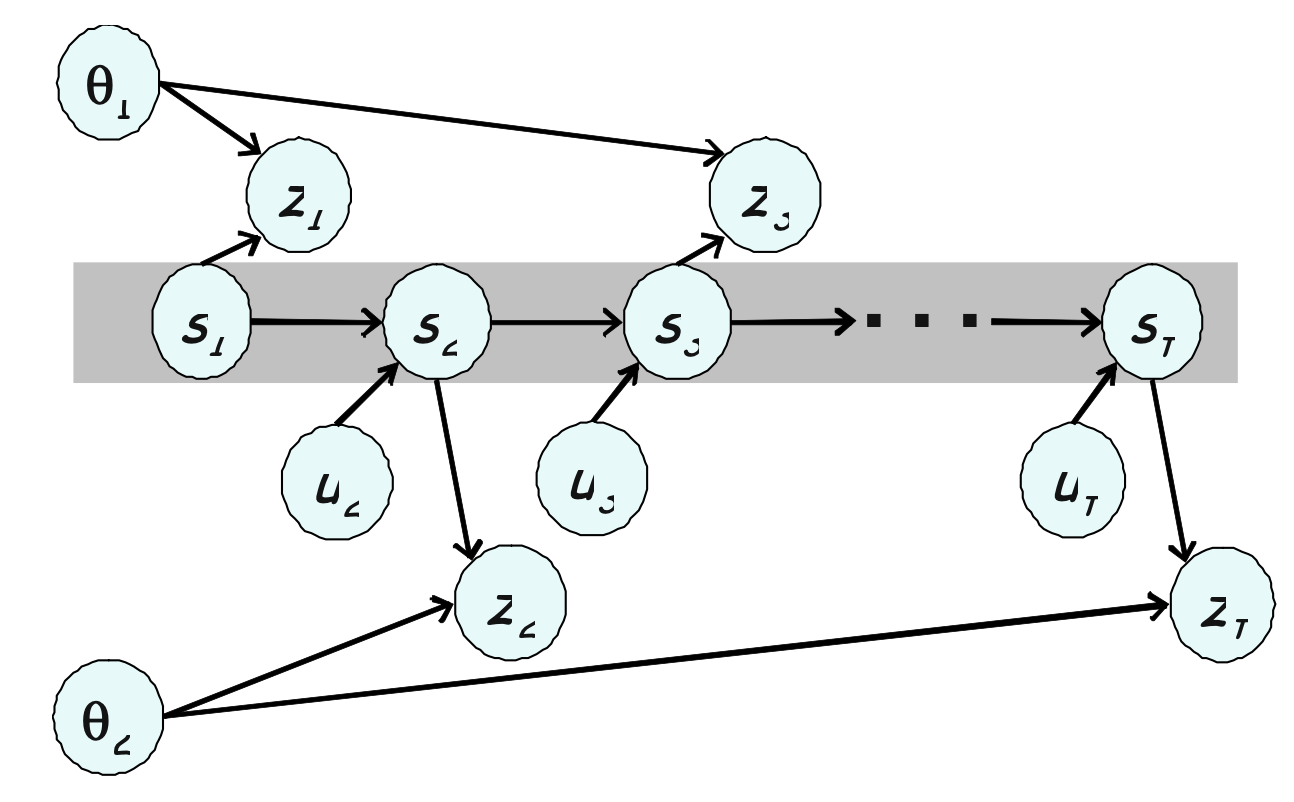
시간 t에 대한 로봇의 자세를 $s_t$로 이 자세는 이전의 로봇 자세 $s_{t-1}$과 제어 $u_t$를 실행하여 얻을 수 있습니다.
시간 t에 대한 관측은 $z_t$로 표기하며 로봇의 자세 $s_t$와 관측된 랜드마크 $\theta_{n_t}$로 얻을 수 있습니다.
위 그림의 시나리오 데로 따라가면 랜드마크 1은 t = 1, 3일때 관측되며, 랜드마크 2은 t=2에서 관측됩니다.
회색 공간은 로봇의 전체 경로를 강조하고 있습니다.
이 네트워크를 보면 알수 있지만 이 경로는 두개의 랜드마크를 나타내는 노드로 나누어지게 됩니다.
정리하면 로봇의 실제 주행 경로를 알고 있는 상태에 첫번째 랜드마크의 위치를 안다고 해서
두번쨰 랜드마크의 위치를 구하는데 도움되지 않는다고 할수 있습니다.
랜드마크간 조건부 독립을 이용한 SLAM 사후확률 분해
이 관계를 통해서, 데이터 연관이 주어질때 SLAM 사후확률은 다음의 곱 형태로 구할수 있겠습니다.
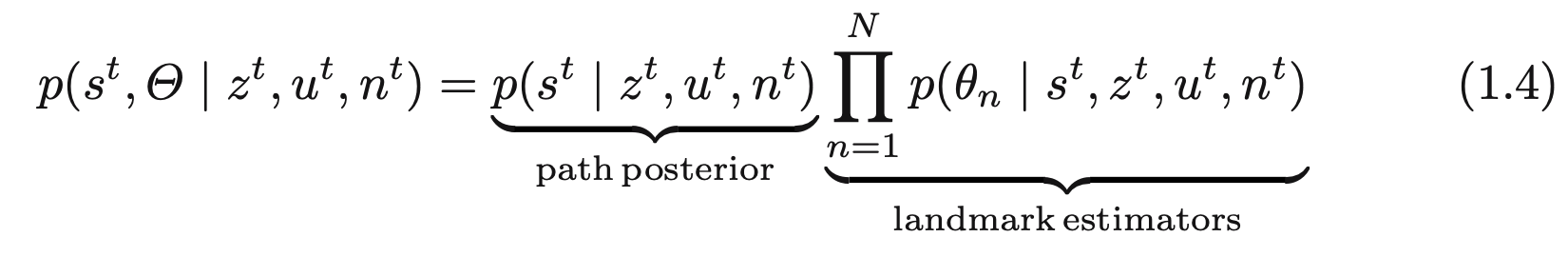
이 분해를 통해 완전 SLAM 사후확률이 N + 1개의 재귀 추정기로 나눌수 있음을 알수 있으며, 1개 추정기는 로봇의 경로에 대한 것이고,
N개의 로봇의 경로 추정에 조건부이며, 서로의 랜드마크 위치에독립적인 추정기들로 이루어집니다.
위 분해된 사후확률은 파티클 필터를 이용하여 효과적으로 근사화 할수 있으며, 이 파티클 필터의 파티클들은 로봇의 샘플 경로가 됩니다.
여기서 각 파티클들은 N개의 독립 랜드마크 추정기에 붙여져(EKF로 구현됨), 해당 랜드마크에 대한 로봇의 자세가 되겠습니다.
랜드마크 필터들이 각각의 랜드마크의 자세를 추정하므로, 각 필터는 저차원이 되겠습니다.
그래서 전체적으로 N x M개의 칼만 필터가 사용됩니다.
이 파티클 필터를 갱신하는 알고리즘을 FastSLAM이라 부르겠습니다.
통계학에 친숙한 사람이라면 이 FastSLAM이 Rao-Blackwellized Prticle Filter를 구현한 것임을 알수 있을 겁니다.
'로봇 > SLAM' 카테고리의 다른 글
| FastSLAM - 2. SLAM 문제 (0) | 2020.07.07 |
|---|---|
| FastSLAM - 1.6 FastSLAM+ (0) | 2020.07.07 |
| FastSLAM - 1.5 SLAM의 구조와 희소 (0) | 2020.07.06 |
| FastSLAM - 1.4 확장칼만필터 (0) | 2020.07.06 |
| FastSLAM - 1.3 사후 추정 (0) | 2020.07.06 |