지난번에 EKF SLAM을 살펴본데에 이어서
FastSLAM 알고리즘 시뮬레이션을 봅시다.
"""
FastSLAM 1.0 example
author: Atsushi Sakai (@Atsushi_twi)
"""
import numpy as np
import math
import matplotlib.pyplot as plt
# Fast SLAM covariance
Q = np.diag([3.0, math.radians(10.0)])**2
R = np.diag([1.0, math.radians(20.0)])**2
# Simulation parameter
Qsim = np.diag([0.3, math.radians(2.0)])**2
Rsim = np.diag([0.5, math.radians(10.0)])**2
OFFSET_YAWRATE_NOISE = 0.01
DT = 0.5 # time tick [s]
SIM_TIME = 90.0 # simulation time [s]
MAX_RANGE = 20.0 # maximum observation range
M_DIST_TH = 2.0 # Threshold of Mahalanobis distance for data association.
STATE_SIZE = 3 # State size [x,y,yaw]
LM_SIZE = 2 # LM srate size [x,y]
N_PARTICLE = 50 # number of particle
NTH = N_PARTICLE / 1.5 # Number of particle for re-sampling
show_animation = True노이즈 값들을 지정해주고,
아래에는 시간 간격, 시뮬레이션 시간, 마할라노비스거리 임계치, 파티클 개수, 리샘플링할 파티클 수를 설정합니다.
리샘플링할 파티클 수 인 NTH는 50/1.5 = 34개 정도가 되겠습니다.
def main():
print(__file__ + " start!!")
time = 0.0
# RFID positions [x, y]
RFID = np.array([[10.0, -2.0],
[15.0, 10.0],
[15.0, 15.0],
[10.0, 20.0],
[3.0, 15.0],
[-5.0, 20.0],
[-5.0, 5.0],
[-10.0, 15.0]
])
N_LM = RFID.shape[0]
# State Vector [x y yaw v]'
xEst = np.matrix(np.zeros((STATE_SIZE, 1)))
xTrue = np.matrix(np.zeros((STATE_SIZE, 1)))
xDR = np.matrix(np.zeros((STATE_SIZE, 1))) # Dead reckoning
# history
hxEst = xEst
hxTrue = xTrue
hxDR = xTrue
particles = [Particle(N_LM) for i in range(N_PARTICLE)]
while SIM_TIME >= time:
time += DT
u = calc_input(time)
xTrue, z, xDR, ud = observation(xTrue, xDR, u, RFID)
particles = fast_slam1(particles, ud, z)
xEst = calc_final_state(particles)
x_state = xEst[0: STATE_SIZE]
# store data history
hxEst = np.hstack((hxEst, x_state))
hxDR = np.hstack((hxDR, xDR))
hxTrue = np.hstack((hxTrue, xTrue))
if show_animation:
plt.cla()
plt.plot(RFID[:, 0], RFID[:, 1], "*k")
for i in range(N_PARTICLE):
plt.plot(particles[i].x, particles[i].y, ".r")
plt.plot(particles[i].lm[:, 0], particles[i].lm[:, 1], "xb")
plt.plot(np.array(hxTrue[0, :]).flatten(),
np.array(hxTrue[1, :]).flatten(), "-b")
plt.plot(np.array(hxDR[0, :]).flatten(),
np.array(hxDR[1, :]).flatten(), "-k")
plt.plot(np.array(hxEst[0, :]).flatten(),
np.array(hxEst[1, :]).flatten(), "-r")
plt.plot(xEst[0], xEst[1], "xk")
plt.axis("equal")
plt.grid(True)
plt.pause(0.001)
if __name__ == '__main__':
main()
매번 하던것 처럼 매인함수에서 애니메이션과 루프문을 제외하고 앞부분 부터 보겠습니다.
def main():
print(__file__ + " start!!")
time = 0.0
# RFID positions [x, y]
RFID = np.array([[10.0, -2.0],
[15.0, 10.0],
[15.0, 15.0],
[10.0, 20.0],
[3.0, 15.0],
[-5.0, 20.0],
[-5.0, 5.0],
[-10.0, 15.0]
])
N_LM = RFID.shape[0]
# State Vector [x y yaw v]'
xEst = np.matrix(np.zeros((STATE_SIZE, 1)))
xTrue = np.matrix(np.zeros((STATE_SIZE, 1)))
xDR = np.matrix(np.zeros((STATE_SIZE, 1))) # Dead reckoning
# history
hxEst = xEst
hxTrue = xTrue
hxDR = xTrue
particles = [Particle(N_LM) for i in range(N_PARTICLE)]RFID 8개를 만들어 주고, 랜드마크의 개수를 구합니다.
추정 상태와 실제상태, 추측항법 상태들에 대한 공간을 만들어주고
이들을 기록할 history 변수도 만들어 줍니다.
파티클 갯수만큼 파티클들을 생성해 줍니다.
파티클들이 생성되니 파티클 클래스를 보겠습니다.
class Particle:
def __init__(self, N_LM):
self.w = 1.0 / N_PARTICLE
self.x = 0.0
self.y = 0.0
self.yaw = 0.0
# landmark x-y positions
self.lm = np.matrix(np.zeros((N_LM, LM_SIZE)))
# landmark position covariance
self.lmP = np.matrix(np.zeros((N_LM * LM_SIZE, LM_SIZE)))
파티클 클래스는
파티클의 가중치(초기시 균일분포)와 x,y, yaw 값이 있으며
이 파티클에 해당하는 랜드마크들의 위치와 랜드마크들에 대한 공분산을 가지고 있습니다.
메인 함수에서 랜드마크 개수 N_LM으로 8개를 전달받아 랜드마크 크기 LM_SIZE는 x, y 두개만 존재하므로 2이니
lm은 (8, 2)의 행렬이고, lmP는 (16, 2)의 행렬이 되겠습니다.
이제 메인함수문의 루프문으로 돌아가겠습니다.
while SIM_TIME >= time:
time += DT
u = calc_input(time)
xTrue, z, xDR, ud = observation(xTrue, xDR, u, RFID)
particles = fast_slam1(particles, ud, z)
xEst = calc_final_state(particles)
x_state = xEst[0: STATE_SIZE]히스토리 변수와 애니메이션을 제외하고 보면
calc_input에서 제어 입력을 얻고
관측을 수행한다음
fastslam 알고리즘으로 파티클들을 구하고
최종 상태값을 구하는 순서가 되겠습니다.
우선 제어 입력 계산 함수는 시간을 인자로 받는데 이를 살펴보면
def calc_input(time):
if time <= 3.0:
v = 0.0
yawrate = 0.0
else:
v = 1.0 # [m/s]
yawrate = 0.1 # [rad/s]
u = np.matrix([v, yawrate]).T
return u
이 함수는 시간이 3초 이하일때 선속도 0, 각속도 0을 반환하며
그 외에는 기존에 전달하던 대로 선속도와 각속도를 반환합니다.
그 다음 관측 함수를 보겠습니다.
def observation(xTrue, xd, u, RFID):
xTrue = motion_model(xTrue, u)
# add noise to gps x-y
z = np.matrix(np.zeros((0, 3)))
for i in range(len(RFID[:, 0])):
dx = RFID[i, 0] - xTrue[0, 0]
dy = RFID[i, 1] - xTrue[1, 0]
d = math.sqrt(dx**2 + dy**2)
angle = pi_2_pi(math.atan2(dy, dx) - xTrue[2, 0])
if d <= MAX_RANGE:
dn = d + np.random.randn() * Qsim[0, 0] # add noise
anglen = angle + np.random.randn() * Qsim[1, 1] # add noise
zi = np.matrix([dn, pi_2_pi(anglen), i])
z = np.vstack((z, zi))
# add noise to input
ud1 = u[0, 0] + np.random.randn() * Rsim[0, 0]
ud2 = u[1, 0] + np.random.randn() * Rsim[1, 1] + OFFSET_YAWRATE_NOISE
ud = np.matrix([ud1, ud2]).T
xd = motion_model(xd, ud)
return xTrue, z, xd, ud
관측 함수는 이전 EKF SLAM때와 마찬가지로
1. 실제 상태
2. 관측치들 - 실제 상태와 RFID 사이 거리와 방위, 거리가 센서 범위 안인 관측치들
3. 추측 상태
4. 노이즈 제어 입력
을 정리하여 반환하고
이제 fast SLAM 1함수를 보겠습니다.
def fast_slam1(particles, u, z):
particles = predict_particles(particles, u)
particles = update_with_observation(particles, z)
particles = resampling(particles)
return particles
fast slam 알고리즘은
1. 파티클 예측
2. 관찰 갱신
3. 리샘플링
으로 나누어 수행되며
우선 파티클 예측 단계 부터 보겠습니다..
def predict_particles(particles, u):
for i in range(N_PARTICLE):
px = np.zeros((STATE_SIZE, 1))
px[0, 0] = particles[i].x
px[1, 0] = particles[i].y
px[2, 0] = particles[i].yaw
ud = u + (np.matrix(np.random.randn(1, 2)) * R).T # add noise
px = motion_model(px, ud)
particles[i].x = px[0, 0]
particles[i].y = px[1, 0]
particles[i].yaw = px[2, 0]
return particles
이 함수에서는 모든 파티클에 대해
이전 상태와 노이즈 제어 입력을 동작 모델을 사용하여 파티클의 예측 상태를 구합니다.
그 다음에는 관측 갱신 과정을 보겠습니다.
def update_with_observation(particles, z):
for iz in range(len(z[:, 0])):
lmid = int(z[iz, 2])
for ip in range(N_PARTICLE):
# new landmark
if abs(particles[ip].lm[lmid, 0]) <= 0.01:
particles[ip] = add_new_lm(particles[ip], z[iz, :], Q)
# known landmark
else:
w = compute_weight(particles[ip], z[iz, :], Q)
particles[ip].w *= w
particles[ip] = update_landmark(particles[ip], z[iz, :], Q)
return particles관측 갱신 함수에서는 관측된 관측치들만큼 반복을 수행합니다.
해당 관측된 랜드마크의 아이디 lmid를 구하고,
모든 파티클에 대해 루프를 돌립니다.
인덱스가 ip인 파티클에서
lmid 번째 랜드마크의 x 좌표의 절댓값이 0.01보다 작은 경우
새로운 랜드마크로 판단하여,
ip번째 파티클에 랜드마크 추가 함수가 수행됩니다.
잠깐 랜드마크 추가 함수에는
해당 랜드마크 관측과 이 랜드마크를 추가시킬 파티클이 사용됩니다.
def add_new_lm(particle, z, Q):
r = z[0, 0]
b = z[0, 1]
lm_id = int(z[0, 2])
s = math.sin(pi_2_pi(particle.yaw + b))
c = math.cos(pi_2_pi(particle.yaw + b))
particle.lm[lm_id, 0] = particle.x + r * c
particle.lm[lm_id, 1] = particle.y + r * s
# covariance
Gz = np.matrix([[c, -r * s],
[s, r * c]])
particle.lmP[2 * lm_id:2 * lm_id + 2] = Gz * Q * Gz.T
return particle랜드마크 추가 함수에선
관측의 0번째 값이 거리, 1번째 값이 방위, 2번째 값이 아이디이므로 이들을 초기화 해주고,
해당 파티클에 대한 랜드마크의 사인각과 코사인 각을 구한 다음
파티클의 랜드마크 리스트에 해당 아이디의 랜드마크 위치 값을 추가시켜 줍니다.
그다음 파티클의 랜드마크 공분산을 계산하여 추가 시켜줍시다.
이제 관측 갱신으로 돌아값시다.
def update_with_observation(particles, z):
for iz in range(len(z[:, 0])):
lmid = int(z[iz, 2])
for ip in range(N_PARTICLE):
# new landmark
if abs(particles[ip].lm[lmid, 0]) <= 0.01:
particles[ip] = add_new_lm(particles[ip], z[iz, :], Q)
# known landmark
else:
w = compute_weight(particles[ip], z[iz, :], Q)
particles[ip].w *= w
particles[ip] = update_landmark(particles[ip], z[iz, :], Q)
return particles조금전에 파티클에 랜드마크 추가 로직을 살펴보았으니
이 파티클아 알고있는 랜드마크를 관측하는 경우를 살펴보겠습니다.
현재 파티클과 해당 관측을 가중치 계산 함수에 전달하여 가중치를 구하는데
def compute_weight(particle, z, Q):
lm_id = int(z[0, 2])
xf = np.matrix(particle.lm[lm_id, :]).T
Pf = np.matrix(particle.lmP[2 * lm_id:2 * lm_id + 2])
zp, Hv, Hf, Sf = compute_jacobians(particle, xf, Pf, Q)
dx = z[0, 0: 2].T - zp
dx[1, 0] = pi_2_pi(dx[1, 0])
S = particle.lmP[2 * lm_id:2 * lm_id + 2]
try:
invS = np.linalg.inv(S)
except np.linalg.linalg.LinAlgError:
print("singuler")
return 1.0
num = math.exp(-0.5 * dx.T * invS * dx)
den = 2.0 * math.pi * math.sqrt(np.linalg.det(S))
w = num / den
return w일단 관측치로부터 랜드마크 아이디를 구하고
파티클로부터 랜드마크의 상태와 공분산을 추출합니다.
현재 파티클과 추출한 랜드마크, 공분산으로 자코비안을 계산하여 얻은 변수들로
추정 관측치와 실제 관측치 차이인 dx를 구하고
dx의 1번 인덱스 각도를 변환해 줍시다.
파티클의 해당 랜드마크 공분산을 S라는 변수에 담아
역변환을 수행하고, 가중치에 사용할 분자 분모를 계산해
ip 번째 파티클의 lm_id인 랜드마크에 대한 최종적인 가중치를 구합니다.
def update_with_observation(particles, z):
for iz in range(len(z[:, 0])):
lmid = int(z[iz, 2])
for ip in range(N_PARTICLE):
# new landmark
if abs(particles[ip].lm[lmid, 0]) <= 0.01:
particles[ip] = add_new_lm(particles[ip], z[iz, :], Q)
# known landmark
else:
w = compute_weight(particles[ip], z[iz, :], Q)
particles[ip].w *= w
particles[ip] = update_landmark(particles[ip], z[iz, :], Q)
return particles다시 관측 갱신 함수로 돌아와
ip번쨰 파티클의 가중치에 방금 구한 w를 곱해주고,
랜드마크 갱신을 수행합니다.
def update_landmark(particle, z, Q):
lm_id = int(z[0, 2])
xf = np.matrix(particle.lm[lm_id, :]).T
Pf = np.matrix(particle.lmP[2 * lm_id:2 * lm_id + 2, :])
zp, Hv, Hf, Sf = compute_jacobians(particle, xf, Pf, Q)
dz = z[0, 0: 2].T - zp
dz[1, 0] = pi_2_pi(dz[1, 0])
xf, Pf = update_KF_with_cholesky(xf, Pf, dz, Q, Hf)
particle.lm[lm_id, :] = xf.T
particle.lmP[2 * lm_id:2 * lm_id + 2, :] = Pf
return particle
다시 랜드마크의 아이디와 상태, 공분산을 구하고
자코비안을 계산한 다음, 실제 관측과 예측관측사이 오차인 dz를 계산합니다.
그 다음 칼만 필터 갱신 함수를 호출하여 수행합니다.
def update_KF_with_cholesky(xf, Pf, v, Q, Hf):
PHt = Pf * Hf.T
S = Hf * PHt + Q
S = (S + S.T) * 0.5
SChol = np.linalg.cholesky(S).T
SCholInv = np.linalg.inv(SChol)
W1 = PHt * SCholInv
W = W1 * SCholInv.T
x = xf + W * v
P = Pf - W1 * W1.T
return x, P칼만 필터 알고리즘으로 랜드마크의 추정 상태와 추정 공분산을 계산한 뒤 반환하여
def update_landmark(particle, z, Q):
lm_id = int(z[0, 2])
xf = np.matrix(particle.lm[lm_id, :]).T
Pf = np.matrix(particle.lmP[2 * lm_id:2 * lm_id + 2, :])
zp, Hv, Hf, Sf = compute_jacobians(particle, xf, Pf, Q)
dz = z[0, 0: 2].T - zp
dz[1, 0] = pi_2_pi(dz[1, 0])
xf, Pf = update_KF_with_cholesky(xf, Pf, dz, Q, Hf)
particle.lm[lm_id, :] = xf.T
particle.lmP[2 * lm_id:2 * lm_id + 2, :] = Pf
return particle랜드마크 갱신 함수에서는 방금전에 구한 랜드마크의 추정 상태와 공분산을
ip번째 파티클의 lm_id번째 랜드마크의 상태와 공분산에 넣어 주면
랜드마크가 갱신된 파티클을 반환하게 됩니다.
def update_with_observation(particles, z):
for iz in range(len(z[:, 0])):
lmid = int(z[iz, 2])
for ip in range(N_PARTICLE):
# new landmark
if abs(particles[ip].lm[lmid, 0]) <= 0.01:
particles[ip] = add_new_lm(particles[ip], z[iz, :], Q)
# known landmark
else:
w = compute_weight(particles[ip], z[iz, :], Q)
particles[ip].w *= w
particles[ip] = update_landmark(particles[ip], z[iz, :], Q)
return particles하나의 파티클에 대해 가지고 관측된 랜드마크들을 추가하거나 갱신 작업을 수행하고
이를 반복하여 모든 파티클에 대해서 수행됩니다.
결과로 구한 파티클 집합을 반환해줍니다.
def fast_slam1(particles, u, z):
particles = predict_particles(particles, u)
particles = update_with_observation(particles, z)
particles = resampling(particles)
return particles
fast_slam1의 관측 갱신 함수로 모든 파티클과 각 파티클들의 랜드마크들을 갱신시킨뒤에
리샘플링을 수행하여야 합니다.
def resampling(particles):
"""
low variance re-sampling
"""
particles = normalize_weight(particles)
pw = []
for i in range(N_PARTICLE):
pw.append(particles[i].w)
pw = np.matrix(pw)
Neff = 1.0 / (pw * pw.T)[0, 0] # Effective particle number
# print(Neff)
if Neff < NTH: # resampling
wcum = np.cumsum(pw)
base = np.cumsum(pw * 0.0 + 1 / N_PARTICLE) - 1 / N_PARTICLE
resampleid = base + np.random.rand(base.shape[1]) / N_PARTICLE
inds = []
ind = 0
for ip in range(N_PARTICLE):
while ((ind < wcum.shape[1] - 1) and (resampleid[0, ip] > wcum[0, ind])):
ind += 1
inds.append(ind)
tparticles = particles[:]
for i in range(len(inds)):
particles[i].x = tparticles[inds[i]].x
particles[i].y = tparticles[inds[i]].y
particles[i].yaw = tparticles[inds[i]].yaw
particles[i].lm = tparticles[inds[i]].lm[:, :]
particles[i].lmP = tparticles[inds[i]].lmP[:, :]
particles[i].w = 1.0 / N_PARTICLE
return particles
리샘플링 단계에서는 우선 파티클들의 가중치 정규화 과정을 수행하는데
def normalize_weight(particles):
sumw = sum([p.w for p in particles])
try:
for i in range(N_PARTICLE):
particles[i].w /= sumw
except ZeroDivisionError:
for i in range(N_PARTICLE):
particles[i].w = 1.0 / N_PARTICLE
return particles
return particles모든 파티클들의 가중치를 모두 합한 후에
기존의 파티클 가중치에 가중치 합을 나누어 정규화 해줍니다.
def resampling(particles):
"""
low variance re-sampling
"""
particles = normalize_weight(particles)
pw = []
for i in range(N_PARTICLE):
pw.append(particles[i].w)
pw = np.matrix(pw)
Neff = 1.0 / (pw * pw.T)[0, 0] # Effective particle number
# print(Neff)
if Neff < NTH: # resampling
wcum = np.cumsum(pw)
base = np.cumsum(pw * 0.0 + 1 / N_PARTICLE) - 1 / N_PARTICLE
resampleid = base + np.random.rand(base.shape[1]) / N_PARTICLE
inds = []
ind = 0
for ip in range(N_PARTICLE):
while ((ind < wcum.shape[1] - 1) and (resampleid[0, ip] > wcum[0, ind])):
ind += 1
inds.append(ind)
tparticles = particles[:]
for i in range(len(inds)):
particles[i].x = tparticles[inds[i]].x
particles[i].y = tparticles[inds[i]].y
particles[i].yaw = tparticles[inds[i]].yaw
particles[i].lm = tparticles[inds[i]].lm[:, :]
particles[i].lmP = tparticles[inds[i]].lmP[:, :]
particles[i].w = 1.0 / N_PARTICLE
return particles
pw 변수에다가 파티클들의 모든 정규화된 가중치들을 담아주고,
파티클 계수 Neff를 구합니다.
리샘플링 단계는 Neff가 NTH보다 작으면 리샘플링 단계가 수행되는데,
우선 가중치를 누적한 wcum과 base, 그리고 리샘플 아이디들을 구합니다.
모든 파티클에 대해 반복을 수행하는데
아래의 로직은 저분포 리샘플링 알고리즘 내용을 확인해야해야 하지만
0111222222222222222222와 같은 식으로 파티클들에 인덱스가 지정됩니다.
그 다음 임시 파티클 집합을 생성해주고,
위 인덱스 리스트의 경우 2가 4번쨰부터 20번째 까지 온다고 가정하면,
4~20번째 파티클들의 값이 2번째 파티클의 값으로 복사가 됩니다.
이와 같은 식으로 가장 인덱스가 많은 파티클 위주로 살아남고,
인덱스가 적은 파티클의 경우 소멸하게 됩니다.
위와 같은 과정을 통해 파티클 리샘플링이 수행됩니다.
while SIM_TIME >= time:
time += DT
u = calc_input(time)
xTrue, z, xDR, ud = observation(xTrue, xDR, u, RFID)
particles = fast_slam1(particles, ud, z)
xEst = calc_final_state(particles)
x_state = xEst[0: STATE_SIZE]fastslam1 함수로 리샘플링된 파티클 집합을 구하였다면
이 파티클들로부터 최종 상태를 구하여야 합니다.
def calc_final_state(particles):
xEst = np.zeros((STATE_SIZE, 1))
particles = normalize_weight(particles)
for i in range(N_PARTICLE):
xEst[0, 0] += particles[i].w * particles[i].x
xEst[1, 0] += particles[i].w * particles[i].y
xEst[2, 0] += particles[i].w * particles[i].yaw
xEst[2, 0] = pi_2_pi(xEst[2, 0])
# print(xEst)
return xEst최종 상태 계산 함수에서는 파티클 집합을 매개변수로 받으며,
우선 로봇의 추정 상태를 초기화 부터 해줍시다.
다음에는 파티클들의 정규화를 수행한 뒤
모든 파티클의 가중치와 파티클의 상태의 곱의 합을
로봇의 추정 상태가 됩니다.
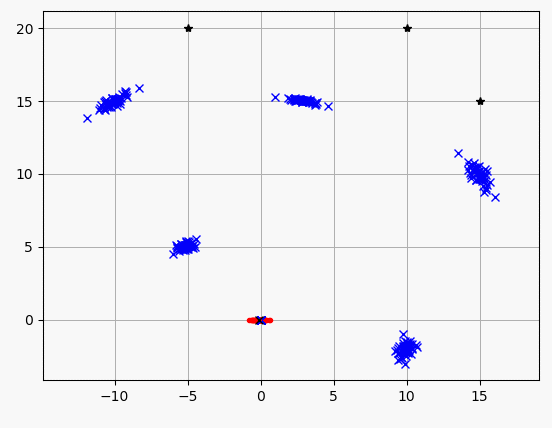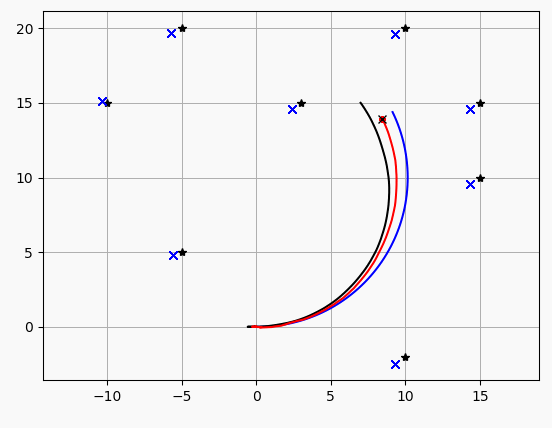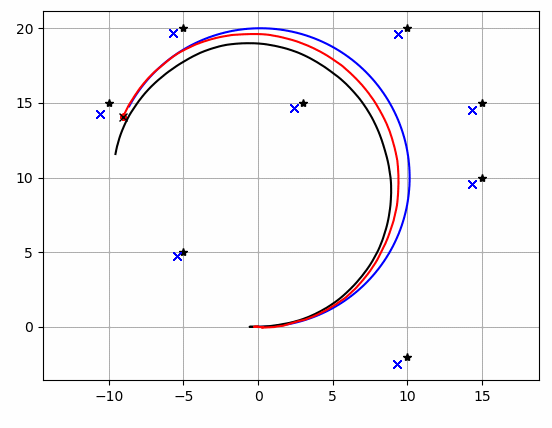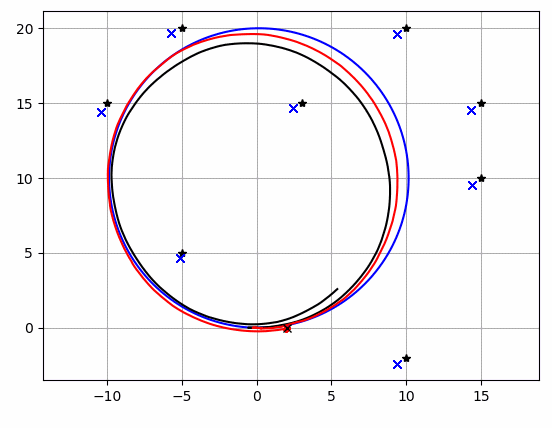
전체적인 과정을 정리하면
우선 파티클들을 균일 분포로 퍼트렸고,
이 파티클들을 동작 모델에 따라 이동 시킨다음에
각 파티클을 관측된 모든 랜드마크에 대해 칼만 필터를 적용하여 랜드마크들의 상태와 공분산을 추정하였습니다.
리샘플링 알고리즘으로 높은 확률을 가진 파티클들만 남도록 만들었습니다.
그 다음 이 리샘플링된 파티클의 가중치와 상태 값을 이용하여 로봇의 최종 추정 상태를 계산하였습니다.
FastSLAM에서는 위 과정들이 계속 반복됩니다.
"""
FastSLAM 1.0 example
author: Atsushi Sakai (@Atsushi_twi)
"""
import numpy as np
import math
import matplotlib.pyplot as plt
# Fast SLAM covariance
Q = np.diag([3.0, math.radians(10.0)])**2
R = np.diag([1.0, math.radians(20.0)])**2
# Simulation parameter
Qsim = np.diag([0.3, math.radians(2.0)])**2
Rsim = np.diag([0.5, math.radians(10.0)])**2
OFFSET_YAWRATE_NOISE = 0.01
DT = 0.3 # time tick [s]
SIM_TIME = 90.0 # simulation time [s]
MAX_RANGE = 20.0 # maximum observation range
M_DIST_TH = 2.0 # Threshold of Mahalanobis distance for data association.
STATE_SIZE = 3 # State size [x,y,yaw]
LM_SIZE = 2 # LM srate size [x,y]
N_PARTICLE = 50 # number of particle
NTH = N_PARTICLE / 1.5 # Number of particle for re-sampling
show_animation = True
class Particle:
def __init__(self, N_LM):
self.w = 1.0 / N_PARTICLE
self.x = 0.0
self.y = 0.0
self.yaw = 0.0
# landmark x-y positions
self.lm = np.matrix(np.zeros((N_LM, LM_SIZE)))
# landmark position covariance
self.lmP = np.matrix(np.zeros((N_LM * LM_SIZE, LM_SIZE)))
def fast_slam1(particles, u, z):
particles = predict_particles(particles, u)
particles = update_with_observation(particles, z)
particles = resampling(particles)
return particles
def normalize_weight(particles):
sumw = sum([p.w for p in particles])
try:
for i in range(N_PARTICLE):
particles[i].w /= sumw
except ZeroDivisionError:
for i in range(N_PARTICLE):
particles[i].w = 1.0 / N_PARTICLE
return particles
return particles
def calc_final_state(particles):
xEst = np.zeros((STATE_SIZE, 1))
particles = normalize_weight(particles)
for i in range(N_PARTICLE):
xEst[0, 0] += particles[i].w * particles[i].x
xEst[1, 0] += particles[i].w * particles[i].y
xEst[2, 0] += particles[i].w * particles[i].yaw
xEst[2, 0] = pi_2_pi(xEst[2, 0])
# print(xEst)
return xEst
def predict_particles(particles, u):
for i in range(N_PARTICLE):
px = np.zeros((STATE_SIZE, 1))
px[0, 0] = particles[i].x
px[1, 0] = particles[i].y
px[2, 0] = particles[i].yaw
ud = u + (np.matrix(np.random.randn(1, 2)) * R).T # add noise
px = motion_model(px, ud)
particles[i].x = px[0, 0]
particles[i].y = px[1, 0]
particles[i].yaw = px[2, 0]
return particles
def add_new_lm(particle, z, Q):
r = z[0, 0]
b = z[0, 1]
lm_id = int(z[0, 2])
s = math.sin(pi_2_pi(particle.yaw + b))
c = math.cos(pi_2_pi(particle.yaw + b))
particle.lm[lm_id, 0] = particle.x + r * c
particle.lm[lm_id, 1] = particle.y + r * s
# covariance
Gz = np.matrix([[c, -r * s],
[s, r * c]])
particle.lmP[2 * lm_id:2 * lm_id + 2] = Gz * Q * Gz.T
return particle
def compute_jacobians(particle, xf, Pf, Q):
dx = xf[0, 0] - particle.x
dy = xf[1, 0] - particle.y
d2 = dx**2 + dy**2
d = math.sqrt(d2)
zp = np.matrix([[d, pi_2_pi(math.atan2(dy, dx) - particle.yaw)]]).T
Hv = np.matrix([[-dx / d, -dy / d, 0.0],
[dy / d2, -dx / d2, -1.0]])
Hf = np.matrix([[dx / d, dy / d],
[-dy / d2, dx / d2]])
Sf = Hf * Pf * Hf.T + Q
return zp, Hv, Hf, Sf
def update_KF_with_cholesky(xf, Pf, v, Q, Hf):
PHt = Pf * Hf.T
S = Hf * PHt + Q
S = (S + S.T) * 0.5
SChol = np.linalg.cholesky(S).T
SCholInv = np.linalg.inv(SChol)
W1 = PHt * SCholInv
W = W1 * SCholInv.T
x = xf + W * v
P = Pf - W1 * W1.T
return x, P
def update_landmark(particle, z, Q):
lm_id = int(z[0, 2])
xf = np.matrix(particle.lm[lm_id, :]).T
Pf = np.matrix(particle.lmP[2 * lm_id:2 * lm_id + 2, :])
zp, Hv, Hf, Sf = compute_jacobians(particle, xf, Pf, Q)
dz = z[0, 0: 2].T - zp
dz[1, 0] = pi_2_pi(dz[1, 0])
xf, Pf = update_KF_with_cholesky(xf, Pf, dz, Q, Hf)
particle.lm[lm_id, :] = xf.T
particle.lmP[2 * lm_id:2 * lm_id + 2, :] = Pf
return particle
def compute_weight(particle, z, Q):
lm_id = int(z[0, 2])
xf = np.matrix(particle.lm[lm_id, :]).T
Pf = np.matrix(particle.lmP[2 * lm_id:2 * lm_id + 2])
zp, Hv, Hf, Sf = compute_jacobians(particle, xf, Pf, Q)
dx = z[0, 0: 2].T - zp
dx[1, 0] = pi_2_pi(dx[1, 0])
S = particle.lmP[2 * lm_id:2 * lm_id + 2]
try:
invS = np.linalg.inv(S)
except np.linalg.linalg.LinAlgError:
print("singuler")
return 1.0
num = math.exp(-0.5 * dx.T * invS * dx)
den = 2.0 * math.pi * math.sqrt(np.linalg.det(S))
w = num / den
return w
def update_with_observation(particles, z):
for iz in range(len(z[:, 0])):
lmid = int(z[iz, 2])
for ip in range(N_PARTICLE):
# new landmark
if abs(particles[ip].lm[lmid, 0]) <= 0.01:
particles[ip] = add_new_lm(particles[ip], z[iz, :], Q)
# known landmark
else:
w = compute_weight(particles[ip], z[iz, :], Q)
particles[ip].w *= w
particles[ip] = update_landmark(particles[ip], z[iz, :], Q)
return particles
def resampling(particles):
"""
low variance re-sampling
"""
particles = normalize_weight(particles)
pw = []
for i in range(N_PARTICLE):
pw.append(particles[i].w)
pw = np.matrix(pw)
Neff = 1.0 / (pw * pw.T)[0, 0] # Effective particle number
# print(Neff)
if Neff < NTH: # resampling
wcum = np.cumsum(pw)
base = np.cumsum(pw * 0.0 + 1 / N_PARTICLE) - 1 / N_PARTICLE
resampleid = base + np.random.rand(base.shape[1]) / N_PARTICLE
inds = []
ind = 0
for ip in range(N_PARTICLE):
while ((ind < wcum.shape[1] - 1) and (resampleid[0, ip] > wcum[0, ind])):
ind += 1
inds.append(ind)
tparticles = particles[:]
for i in range(len(inds)):
particles[i].x = tparticles[inds[i]].x
particles[i].y = tparticles[inds[i]].y
particles[i].yaw = tparticles[inds[i]].yaw
particles[i].lm = tparticles[inds[i]].lm[:, :]
particles[i].lmP = tparticles[inds[i]].lmP[:, :]
particles[i].w = 1.0 / N_PARTICLE
return particles
def calc_input(time):
if time <= 3.0:
v = 0.0
yawrate = 0.0
else:
v = 1.0 # [m/s]
yawrate = 0.1 # [rad/s]
u = np.matrix([v, yawrate]).T
return u
def observation(xTrue, xd, u, RFID):
xTrue = motion_model(xTrue, u)
# add noise to gps x-y
z = np.matrix(np.zeros((0, 3)))
for i in range(len(RFID[:, 0])):
dx = RFID[i, 0] - xTrue[0, 0]
dy = RFID[i, 1] - xTrue[1, 0]
d = math.sqrt(dx**2 + dy**2)
angle = pi_2_pi(math.atan2(dy, dx) - xTrue[2, 0])
if d <= MAX_RANGE:
dn = d + np.random.randn() * Qsim[0, 0] # add noise
anglen = angle + np.random.randn() * Qsim[1, 1] # add noise
zi = np.matrix([dn, pi_2_pi(anglen), i])
z = np.vstack((z, zi))
# add noise to input
ud1 = u[0, 0] + np.random.randn() * Rsim[0, 0]
ud2 = u[1, 0] + np.random.randn() * Rsim[1, 1] + OFFSET_YAWRATE_NOISE
ud = np.matrix([ud1, ud2]).T
xd = motion_model(xd, ud)
return xTrue, z, xd, ud
def motion_model(x, u):
F = np.matrix([[1.0, 0, 0],
[0, 1.0, 0],
[0, 0, 1.0]])
B = np.matrix([[DT * math.cos(x[2, 0]), 0],
[DT * math.sin(x[2, 0]), 0],
[0.0, DT]])
x = F * x + B * u
x[2, 0] = pi_2_pi(x[2, 0])
return x
def pi_2_pi(angle):
return float((angle + math.pi) % (2*math.pi) - math.pi)
def main():
print(__file__ + " start!!")
time = 0.0
# RFID positions [x, y]
RFID = np.array([[10.0, -2.0],
[15.0, 10.0],
[15.0, 15.0],
[10.0, 20.0],
[3.0, 15.0],
[-5.0, 20.0],
[-5.0, 5.0],
[-10.0, 15.0]
])
N_LM = RFID.shape[0]
# State Vector [x y yaw v]'
xEst = np.matrix(np.zeros((STATE_SIZE, 1)))
xTrue = np.matrix(np.zeros((STATE_SIZE, 1)))
xDR = np.matrix(np.zeros((STATE_SIZE, 1))) # Dead reckoning
# history
hxEst = xEst
hxTrue = xTrue
hxDR = xTrue
particles = [Particle(N_LM) for i in range(N_PARTICLE)]
while SIM_TIME >= time:
time += DT
u = calc_input(time)
xTrue, z, xDR, ud = observation(xTrue, xDR, u, RFID)
particles = fast_slam1(particles, ud, z)
xEst = calc_final_state(particles)
x_state = xEst[0: STATE_SIZE]
# store data history
hxEst = np.hstack((hxEst, x_state))
hxDR = np.hstack((hxDR, xDR))
hxTrue = np.hstack((hxTrue, xTrue))
if show_animation:
plt.cla()
plt.plot(RFID[:, 0], RFID[:, 1], "*k")
for i in range(N_PARTICLE):
plt.plot(particles[i].x, particles[i].y, ".r")
plt.plot(particles[i].lm[:, 0], particles[i].lm[:, 1], "xb")
plt.plot(np.array(hxTrue[0, :]).flatten(),
np.array(hxTrue[1, :]).flatten(), "-b")
plt.plot(np.array(hxDR[0, :]).flatten(),
np.array(hxDR[1, :]).flatten(), "-k")
plt.plot(np.array(hxEst[0, :]).flatten(),
np.array(hxEst[1, :]).flatten(), "-r")
plt.plot(xEst[0], xEst[1], "xk")
plt.axis("equal")
plt.grid(True)
plt.pause(0.001)
if __name__ == '__main__':
main()
'로봇 > SLAM' 카테고리의 다른 글
| GraphSLAM(thrun) - 1. 소개 (0) | 2020.07.08 |
|---|---|
| GraphSLAM(thrun) - 0. 요약 (0) | 2020.07.08 |
| FastSLAM - 3.3 FastSLAM 1.0 알고리즘 (0) | 2020.07.07 |
| FastSLAM - 3. FastSLAM 1.0 (0) | 2020.07.07 |
| FastSLAM - 2.6 강인한 데이터 연관 (0) | 2020.07.07 |