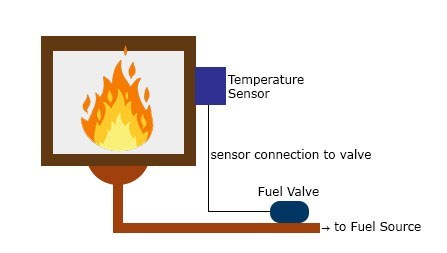
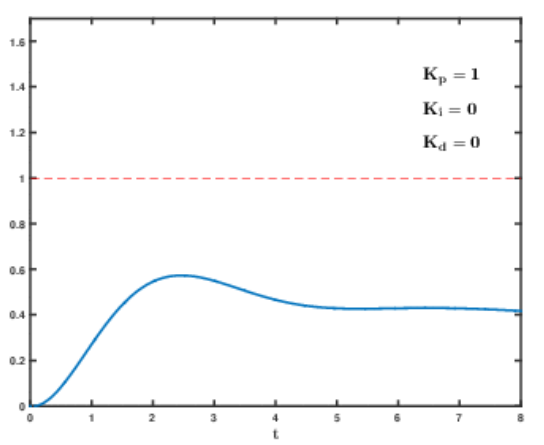
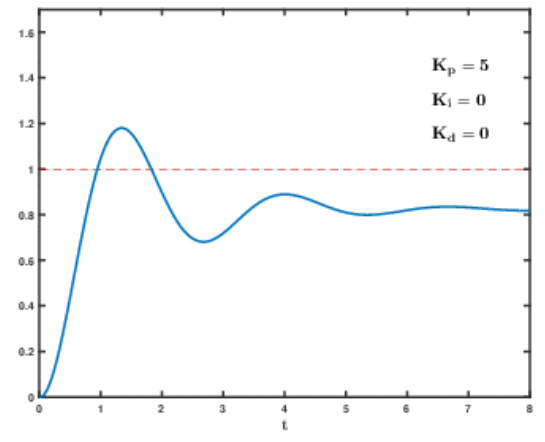
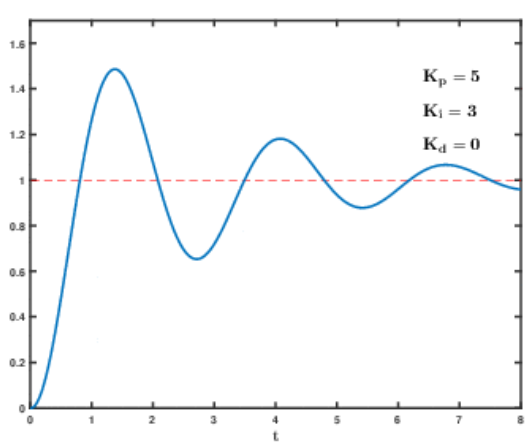
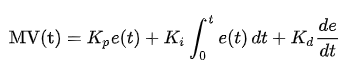오늘 3D 프린팅을 할수 없게되서 대신 코드 정리부터 해보려고한다. 어떻게 정리해나갈지 생각하고자 우선 로터리 엔코더, PID, 모터 제어 코드들을 가져 온 후 어떻게 연동시킬지 생각해본다.
1. 로터리 엔코더
https://howtomechatronics.com/tutorials/arduino/rotary-encoder-works-use-arduino/
#define outputA 6
#define outputB 7
int counter = 0;
int aState;
int aLastState;
void setup() {
pinMode (outputA,INPUT);
pinMode (outputB,INPUT);
Serial.begin (9600);
// Reads the initial state of the outputA
aLastState = digitalRead(outputA);
}
void loop() {
aState = digitalRead(outputA); // Reads the "current" state of the outputA
// If the previous and the current state of the outputA are different, that means a Pulse has occured
if (aState != aLastState){
// If the outputB state is different to the outputA state, that means the encoder is rotating clockwise
if (digitalRead(outputB) != aState) {
counter ++;
} else {
counter --;
}
Serial.print("Position: ");
Serial.println(counter);
}
aLastState = aState; // Updates the previous state of the outputA with the current state
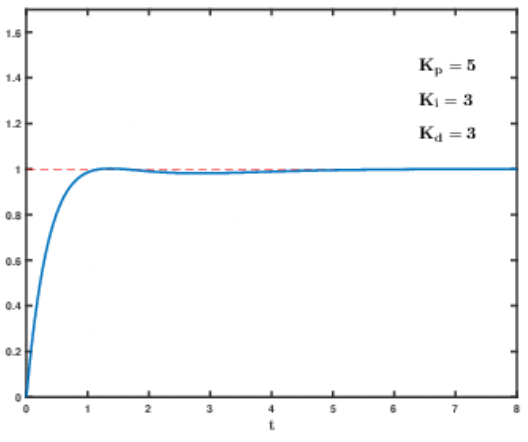
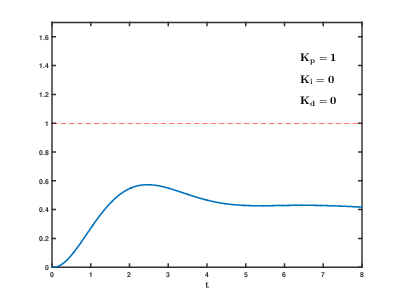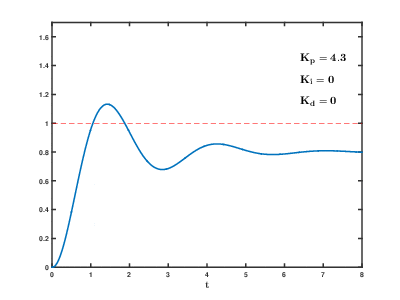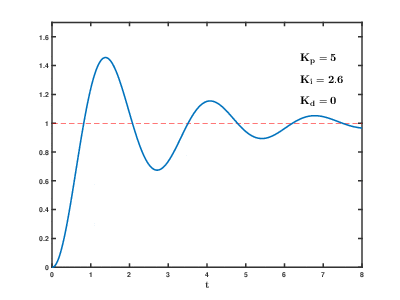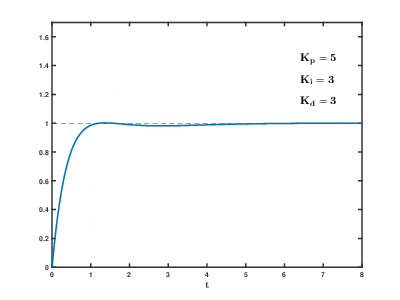
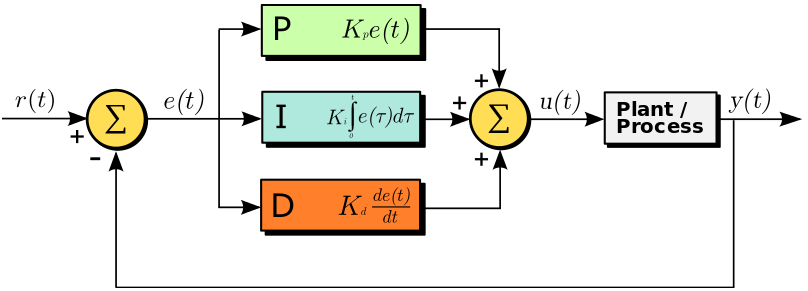
2. PID 예제
https://www.teachmemicro.com/arduino-pid-control-tutorial
//PID constants
double kp = 2
double ki = 5
double kd = 1
unsigned long currentTime, previousTime;
double elapsedTime;
double error;
double lastError;
double input, output, setPoint;
double cumError, rateError;
void setup(){
setPoint = 0; //set point at zero degrees
}
void loop(){
input = analogRead(A0); //read from rotary encoder connected to A0
output = computePID(input);
delay(100);
analogWrite(3, output); //control the motor based on PID value
}
double computePID(double inp){
currentTime = millis(); //get current time
elapsedTime = (double)(currentTime - previousTime); //compute time elapsed from previous computation
error = Setpoint - inp; // determine error
cumError += error * elapsedTime; // compute integral
rateError = (error - lastError)/elapsedTime; // compute derivative
double out = kp*error + ki*cumError + kd*rateError; //PID output
lastError = error; //remember current error
previousTime = currentTime; //remember current time
return out; //have function return the PID output
}
3. DC 모터 제어예제
https://deneb21.tistory.com/281
void setup() {
pinMode(7, OUTPUT);
pinMode(8, OUTPUT);
}
void loop()
{
//최대속도의 50%로 정회전
digitalWrite(7, HIGH);
digitalWrite(8, LOW);
analogWrite(6, 127);
delay(3000);
//최대속도의 50% 역회전
digitalWrite(7, LOW);
digitalWrite(8, HIGH);
analogWrite(6, 127);
delay(3000);
//최대속도로 정회전
digitalWrite(7, HIGH);
digitalWrite(8, LOW);
analogWrite(6, 255);
delay(3000);
//최대속도로 역회전
digitalWrite(7, LOW);
digitalWrite(8, HIGH);
analogWrite(6, 255);
delay(3000);
//정지 (7번핀에 HIGH를 주어도 PWM 핀에 값을 0을 주었기 때문에 정지함)
digitalWrite(7, HIGH);
digitalWrite(8, LOW);
analogWrite(6, 0);
delay(3000);
}
준비는 거의 다되서 진행하려고 하였으나 하필이면 너무 저가의 로터리 엔코더를 사용하다가 제대로 각변화를 측정할수가 없어 더이상 본 과제는 진행할 수가 없다.
상세한 테스트 내용은 오늘 자 문서에 남기고 할수 없이 스테핑 모터를 이용한. 저거 볼 밸런싱 로봇으로 변견해보아야 되겠다.
'로봇 > 전기전자&메카' 카테고리의 다른 글
| 프로토타이핑 - 22. 2020.08.20 보고서 (0) | 2020.08.20 |
|---|---|
| 이글캐드 입문 - 1. PCB, 이글캐드 기초 (0) | 2020.08.20 |
| 프로토타이핑 - 20. 2020.08.19 보고서 (0) | 2020.08.19 |
| 프로토타이핑 - 19. 2020.08.18 보고서 (0) | 2020.08.19 |
| 프로토타이핑 - 18. 2020.08.17 보고서 (0) | 2020.08.17 |