https://www.teachmemicro.com/arduino-pid-control-tutorial
https://ko.m.wikipedia.org/wiki/PID_%EC%A0%9C%EC%96%B4%EA%B8%B0
제어 시스템에서 제어기는 시스템의 출력이 목표 입력값이 되도록 고쳐나가야 합니다. 가장 유명한 제어기중 하나는 PID 제어기로 비례, 적분, 미분의 약어라고 할수 있습니다. 이번에는 아두이노 PID 튜토리얼에 대해서 살펴보면서 이 프로젝트에 제어기가 어떻게 사용되는지 알아봅시다.
앞으로 볼 내용은 아래와 같겠습니다.
1. PID가 뭘까?
1.1 비례 제어
1.2 적분 제어
1.3 미분 제어
2. PID 제어 구현
3. 아두이노 PID 라이브러리
4. 마치면서
1. PID란 무엇일까?
PID는 비례, 적분, 미분의 줄임말이라고 할수 있습니다. 또한 시스템에서 제어기가 요란을 대처하는 방법이라고도 할수 있는데요. 여기서 말하는 제어기는 피드백 시스템에 존재하는 제어기를 말합니다. 그래서 특정 수치값을 읽고 내가 할수있는 일을 하는거라고 할수 있겠습니다.
피드벡 시스템은 출력 결과를 입력으로 되돌려주는 시스템이라고 할수 있는데요. 난로의 불을 제어하는 예제로 한번 배워보겠습니다. 간단한 그림은 아래와 같아요.

여러분들이 일정 온도를 유지하고 싶으면, 센서는 매 시간마다 온도를 측정해주고, 이 측정한 온도가 희망 기준 온도에서 증가하거나 감소했을탠대 이 차이를 오차로 피드백하게 해줍니다.
1.1 비례 제어 Proportional Control
비례 제어는 에러를 얼마나 많이 비례해서 제어할수 있는지를 말하고 있습니다. 예를들자면 위 난로에서 연료를 조절하는 전기 밸브가 있다고 합시다. 오차가 작다면, 설정 값과 측정 값이 일치하도록 밸브는 작은 양의 연료를 줄것이고, 오차가 크다면 벨브로 더 많은 연료를 줄겁니다.
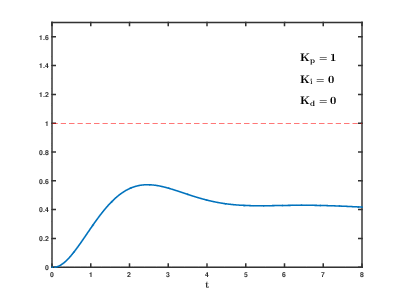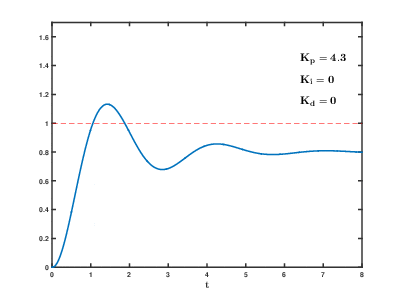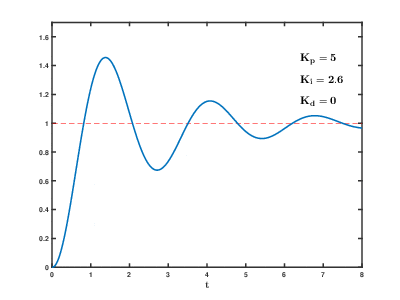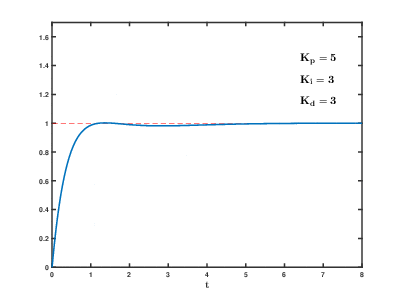
=> 현재 상태에서 오차 값 크기에 비례하여 제어(원하는 값에 빨리 도달)
 |
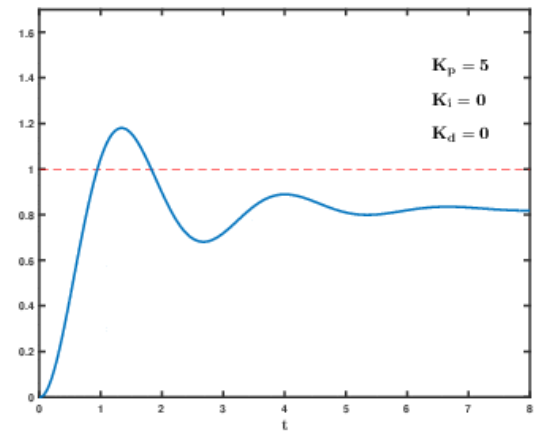 |
- 좌측은 제어이전, 우측은 P 제어 이후
=> 제어 이전에는 출력이 목표 값(1)에 도달하지 못함
=> P 제어 이후 오차 값(목표 값 - 현재 값)만큼 비례해서 신호를 증폭한다.
1.2 적분 제어 Integral Control
비례제어가 요란을 제거해 주었다면, 적분 제어는 이 오프셋 오차를 제거해서 에러를 0으로 만들어줍니다. 제어기는 시간에 대해 오차가 누적되므로 적분 제어기 없이는 오차에 제대로 대응할수 없습니다.
이전의 예시 계속 보면 연료 출력이 증가하거나 감소한 이후에도 초기 위치가 아닌 지점에서 가만히 있게 됩니다. 적분 제어는 이를 감지해서 연료 밸브를 기존의 자리로 돌려주는 역활을 하겠습니다.
=> 정상상태 오차를 제거(누적된 오차로 인해 원하는 값에 수렴하지 못하는 부분을 제거)
 |
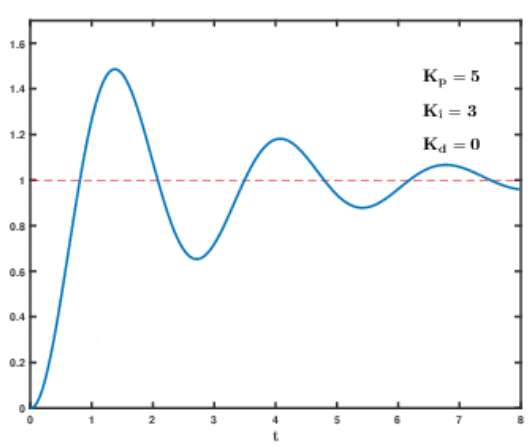 |
- 좌측은 비례제어만 한 결과, 우측은 PI 제어 결과
=> 비례제어만 한 경우 존재하는 정상상태 오차를 적분 제어를 통해 제거함
=> 하지만 오버슛이 심각해짐
1.3 미분 제어 Derivative Control
마지막으로 미분 졔어는 오차의 변화율을 조절시킵니다. 만약 적분 제어에 누적 오차가 보이는 경우에 미분 제어가 이 오차를 예측하여 얼마나 오차가 빠르게 변하는지를 보고 얼마나 고쳐야 할지 찾아냅다. 비례 제어와 적분 제어가 대처하지 못하는 동역학적 에러에 대해서 최적의 동작을 한다고 할수 있겠습니다.
위 난로 예제에서 120도를 설정했지만 130도에서 140도로 올라가는 상황이라고 해봅시다. 비례적분 제어기는 오차의 크기에 대응해서 동작하고는 있지만, 오차가 빠르게 발생하는 경우에서는 대처하기가 어려우나 미분 제어기는 오치의 변화율을 보고 이에 맞게 조절할수가 있습니다.
 |
 |
- 좌측은 PI 제어기, 우측은 PID 제어기
=> 기존의 출력갑이 크게 변하는데 미분 제어를 통해 오버슛을 줄이고 안정하게 만든다
- PID는 위와 같은 형태로 사용하기도 되지만 P 제어기, PI 제어기, PD 제어기만 사용하는 경우도 있음
- PID 제어시 발생가능한 문제
1) 계산된 제어값이 구동기가 동작할수 있는 한계 보다 커 구동기 포화(sturation)이 발생하는 경우
2) 오차 적분값이 크게 누적되어 출력이 설정에 가까워지면 제어가 작아져야하나 큰 값을 출력하여
설정값에 도달하는데 많은 시간이 걸리는 경우
-> 위 문제를 적분기의 와이드업이라 함 => 안티 와이드업 기법으로 PID 제어기를 보완해주어야함
- 제어 파라미터 K_p, K_i, K_d를 제어 이득, 게인이라 부름. 적절한 이득값을 얻는 과정을 튜닝(tunning)이라고 함.
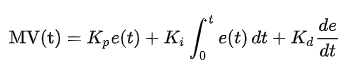
다시 돌아와서
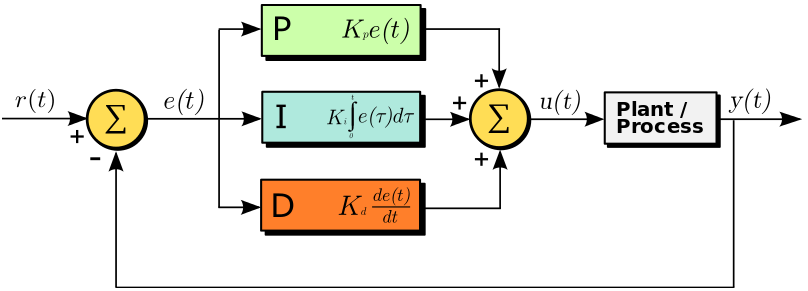
설정 입력값 r(t)가 있고, 출력으로 y(t), 제어 입력 u(t). 오차 e(t)가 있겠습니다. 위 난로 예제에서 보면 r(t)는 희망 온도, y(t)는 실제 온도라 할수 있습니다. e(t)는 실제 온도와 희망 온도의 차이라할수있고, u(t)는 PID 제어기로 교정한 신호의 총합이라 할수 있겠습니다.
원하는 성능을 얻을수 있또록 PID 제어기의 값들을 고치는 작업을 튜닝이라 부르며, 위 그림에서 K 상수들을 잘 조절해주어야 합니다.
코드로 PID 제어하기
아두이노 스캐치에서 PID 제어기를 구현하려면 5개의 파라미터가 필요합니다
-> 비례, 적분, 미분 상수와 입력값과 기준 설정 값
PID 계산은 반드시 내부 루프 함수에 있어야하며, 함수 시작시에는 수행 시간 (elapsed time)을 설정해주어야 합니다. 현재 시간은 millis()로 얻겠습니다.
currentTime = millis();
elapsedTime = currentTime - previousTime;
오차는 설정 지점과 입력의 차이로 얻겠습니다.
error = setPoint - input;
적분 오차는 시간에 대한 누적 오차라 하였으니 아두이노로 구현하려면 다음과 같이 경과시간 * 오차를 해주면 되겠습니다.
cumError += error * elapsedTime;
미분 오차는 에러의 변화율이므로 다음과 같이 하겠습니다.
rateError = (error - lastError)/elapsedTime;
이제 제어 입력 u(t)를 정리하면 아래와 같겠습니다. 여기서 Kp, Ki, Kd는 이전에 설정한 상수가 됩니다.
output = Kp * error + Ki * cumError + Kd * rateError;
마지막으로 다음 반복회차를 위해서 변수들을 아래와 같이 지정해줍시다.
lastError = error;
previousTime = currentTime;
이제 조금 더 제대로 해보면, 다음과같은 휠이 달린 모터가 있다고 해봅시다. 우리는 휠이 저 위치에 있기를 바라고 있습니다. 바퀴에 로터리 엔코더가 재 바퀴 각도에 대한 정보를 알려주므로 우리가 바라는 지점에서의 각도를 0이라 합시다.

휠이 위치를 벗어날떄마다 조정을 해주어야 하는데, 보통 모터는 PWM 펄스 폭 변조를 통해 제어됩니다. 펄스가 넓을수록 모터 회전이 더 빨라집니다.
이제 아두이노에서 다음과 같이 간단한 제어 예시를 구현해봅시다.
//PID constants
double kp = 2
double ki = 5
double kd = 1
unsigned long currentTime, previousTime;
double elapsedTime;
double error;
double lastError;
double input, output, setPoint;
double cumError, rateError;
void setup(){
setPoint = 0; //set point at zero degrees
}
void loop(){
input = analogRead(A0); //read from rotary encoder connected to A0
output = computePID(input);
delay(100);
analogWrite(3, output); //control the motor based on PID value
}
double computePID(double inp){
currentTime = millis(); //get current time
elapsedTime = (double)(currentTime - previousTime); //compute time elapsed from previous computation
error = Setpoint - inp; // determine error
cumError += error * elapsedTime; // compute integral
rateError = (error - lastError)/elapsedTime; // compute derivative
double out = kp*error + ki*cumError + kd*rateError; //PID output
lastError = error; //remember current error
previousTime = currentTime; //remember current time
return out; //have function return the PID output
}위 루프 함수에서는 로터리 엔코더가 휠의 현재 위치를 주고, 그 값이 commputePID()함수의 파라미터로 사용됩니다. 이 함수는 PWM으로 모터 제어에 사용할 값을 반환해 줍니다.
'로봇 > 전기전자&메카' 카테고리의 다른 글
| 프로토타이핑 - 14. 로터리 엔코더 모터 (0) | 2020.08.16 |
|---|---|
| 프로토타이핑 - 13. 로터리 엔코더 (0) | 2020.08.16 |
| 프로토타이핑 - 11. GEKKO (0) | 2020.08.16 |
| 프로토타이핑 - 10. GEKKO를 이용한 역도립진자 시뮬레이션 (0) | 2020.08.16 |
| 프로토타이핑 - 9. 자료 조사 1(2020.08.16) (0) | 2020.08.16 |