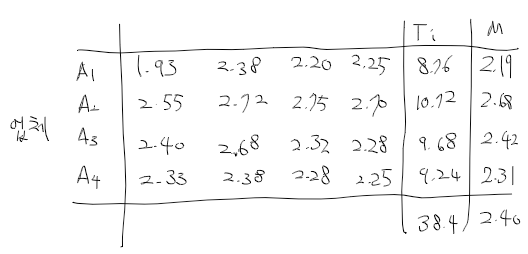집밖은 위험해

분산분석 -> 요인의 수준이 이산형(100, 120)에 따른 종속변수의 영향

회귀분석 : x가 이산이 아닌 연속인경우 분석 방법

공분산분석 : x가 이산형인것도 있고 연속형인것도 두개다 있는 경우

회귀분석 regression analysis

- 독립변수들과 종속변수 간에 관계를 함수식으로 정리하여 분석하는 방법

- 독립/종속변수는 연속값

- 단순 회귀 simple regression : 독립변수가 하나

- 다중 회귀 multiple regression  :독립변수가 여러개

다중 선형 회귀 multiple linear regression

다항 회귀 모형 polynomial regression model

상관계수 correation coefficient

- 두 변수간에 선형적 상관관계에 대해서 나타냄

- 1에 가까우면 양의 상관관계

- -1에 가까우면 음의 상관관계

- 0에 가까우면 선형적 상관관계가 존재하지 않음

단순 선형 회귀 분석 simple linear regresion analysis

- 모형 model

- 관측치 measurements

- 추정식 estimator

- 잔차 residual

최소제곱법 least squared method LSM

다음 데이터가 주어질떄 단순선형회귀를 수행하라

R로 테스트

- 추정량 -0.28928

- 기울기 0.45664 -> pvalue = 3.21e-07로 매우작다 =>유의하다.

- R-squared : 0.9338로 유의함

회귀선의 유의성 검정

- 두 변수 사이에 회귀 관계가 없다면 beta1는 0이되어 다음의 식이 성립합.

- 총제곱합과 잔차제곱합, 회귀제곱합 사이의 관계

결정계수 coefficient of determination R^2

- 회귀식이 얼마나 의미있는지

- R square가 크면 클수록 유의하다.

- 회귀 계수 beta1의 유의성

 -> H0: 회귀관계가 없다. vs H1 : 회귀관계가 있다.

     H0: beta1 = 0 vs H0: beta1 !=0

분석분석표

- 회귀분석의 유의성 검정

분산분석표 분석

유의확률 pvale가 매우 작으므로 h0 기각. 매우 유의

공분산 분석

- 분산분석 + 회귀분석

- 일원 배치 분산분석 : 기계(3대) -> 섬유 제품 강도

- 이원 배치 분산분석 : 기계(3대), 원사두께(얇음,두꺼움) -> 섬유제품 강도

- 공분산 분석 : 기계(3대), 원사 두께(연속적인값, 공변수 covariate) -> 섬유제품 강도

공분산 분석 예시

- 일원배치 예시 : 두개의 사료 (A,B) => 섭취후 체중 y

- 공분산 분석 예시 : 두 사료(A,B), 초기체중 x(연속적인값) => 섭취후 체중 y

이원배치법

- 2개의 요인(독립변수 A, B)와 반응 변수(종속변수) 사이의 관계를 알아보기위한 실험계획

- 독립 변수는 불연속, 종속 변수는 연속적인 값

- 반복이 없는 경우와 있는 경우가 존재

- 반복하는 경우 두 요인간 상호 작용 효과를 검출 가능

이원배치법에서 효과

- 주 효과 main effect : 요인 A의 수준간 차이가 존재하는가

- 상호 작용 효과 interection effect(교호 작용효과) : 요인 A의 서로 다른 수준에서 요인 B의 주효과가 다른가

실험의 랜덤화

- 완전 확률화 계획법 : 두 요인 수준 조건에 순서를 주고, 랜덤한 순서대로 실험

이원 배치법 고정모형(A, B 고정요인- 모수인자)

- 반복의 장점

  인자 조합의 효과를 실험 오차와 분리하여 구할수 있음

  교호작용을 분리하여 검출할수 있어 주효과에 대한 검출이 개선됨

  실험 오차를 구할 수 있음

- 이원배치법의 자료구조

반복이 있는 이원배치 모수모형 (A, B 두인자 모두 고정, 모수인자인경우)

검정 가설

1. 인자 A에 대한 가설

 H0 : alpha1 = alpha2 = ... = 0 ->인자 A의 수준간 효과 차이 없다.

 vs H1 : 적어도 하나의 alphai는 != 0 -> 인자 A의 수준관 효과 차이 있다.

2. 인자 B에 대한 가설

 H0 : beta1 = beta2 = ... = 0 -> 인자 B의 수준간 효과에 차이가 없다

 vs H1 : 적어도 하나의 betai는 != 0 -> 인자 B의 수준간 효과 차이 존재

3. 인자 A와 B의 교호작용에 대한 가설

 H0 : 모든 (alpha beta)ij = 0 -> 교호작용 없다

 vs H1 : 적어도 (alpha beta)ij 중 하나는 0이 아니다 -> 교호작용이 존재

이원배치 분산 분석

이원배치 분산 분석표

이원배치 분산 분석에서 가설검정

1. 인자 A에 대한 가설검정

- 검통 통계량 F0 = MSA / MSE > F(a -1, ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각

 즉, 인자 A가 반응치에 유의한 영향을 준다.

2. 인자 B에 대한 가설검정

- 검통 통계량 F0 = MSB / MSE > F(b -1, ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각

 즉, 인자 B가 반응치에 유의한 영향을 준다.

3. 교호작용 AxB에 대한 가설검정

- 검통 통계량 F0 = MSAxB / MSE > F( (a-1)(b-1), ab(r-1), alpha)=> 유의수준 alpha에서 귀무가설 기각

 즉, 인자 A와 B 사이에 교호작용이 존재한다.

이원배치 분산분석 예제

- 4종류의 사료와 3종류의 돼지 품종이 체중 증가에 미치는 영향

R에서 예제 실습

- 사료와 품종별 boxplot

- 품종별 boxplot 상에서

품종간에 큰 차이는 없어보임

사료별 boxplot

- 사료별 큰 무게 분포를 보인다.

분산분석

- 사료에 대한 유의확률 p val 0.00223로 매우 작음. 귀무가설 기각

 => 사료가 몸무게 증가에 유의한 영향을 준다.

- 나머지의 경우 유의확률이 크므로 귀무가설 채택.

유의확률 = 한계유의수준 = p value

유의수준 = alpha

일원 배치의 구조 모형

- 독립 변수(중요한 요인, 인자)가 하나. 이 변수가 종속 변수(반응치)에 어떤 영향을 미치는가?

1. 모수 인자(고정 인자)

- 관심 대상이 되는 반응온도에서 80도, 100도, 120도를 고정된 인자.

- 최적 조건

- 인자의 수준에 따라 반응치의 모평균이 바뀌는가

2.변량인자 (랜담인자)

- 80~120도사이 같은 구간 반응 온도는 변량 인자

일원 배치법의 구조 모형

오차 epsilon_ij에 대한 가정

- 정규성, 독립성, 불편성, 등분산성

분산분석

귀무가설 H0 : alpha1 = . . . = alpha_a = 0 

   => 수준 효과간 차이가 없다

   ex. 100도 = 120도 = 130도 .. 에서 차이가 없다.

대립가설 H1 : alpha_i 모두 0은 아니다

  => 어떤 수준에서 효과 간 차이가 있다.

변동에 대하여

분산 분석표와 가설 검정 방법

- 검정 통계량 F0 > F(a - 1, a(r-1) ; alpha)이면 유의수준 alpha에서 귀무가설 기각

- 유의확률 p val < 유의수준 alpha이면 대립가설 채택

일원배치 분산분석 예제 - 납품업체간 직물의 마모도에 유의한 차이여부

- 분산분석표

- 일원 배치 분산분석 결과

 검정 통계량 F0 8.78 > F(3, 12; 0.01) = 5.95

 => 귀무가설 기각

납품업체들 간에 직물 마모도 차이가 존재한다.

R로 일원배치 분산분석 실습

- 한계유의수준(유의확률, p val)이 0.00227로 유의수준 0.05보다 작다 => 귀무가설 기각

 업체들간 직물 마모도에 차이가 존재한다.(대립가설 채택)

관련 용어

- 모집단 population : 알고자 하는 대상 집합

- 랜덤 추출 random sampling : 임의의 표본 추출

- 랜덤 표본 random sample : 모집단에서 추출한 표본

- 모수 parameter : 모집단의 특징을 나타내는 값 ex. 모평균, 모분산

- 통계량 statistics : 표본을 이용하여 추정하고자 하는 값에 대한 함수 ex. 표본 평균, 표본 분산

- 추정 estimation : 표본을 이용하여 모집단에 대한 값을 추정하는 과정

- 점추정 point estimation : 모수에 대한 추정

- 구간 추정 interval estimation : 모수에 대한 추정과 추정의 정확률 

- 신뢰 수준 confidence level : 모수가 참이라 속할것으로 기대되는 구간에 못가 포함될 확률 

- 통계적 가설 statistical hypothesis

- 검정 통계량 test statistic 

- 귀무 가설 H0 null hypothesis : 일어날 가능성이 적다고 판단하는 가설. 참인지 판단하고자하는 가설

- 대립가설 H1 : alternative hypothesis : 귀무가설에 대립되는 가설

- 기각역 rejection region : 검정 통계량이 기각역에 들어가는지를 보고 귀무가설 기각여부 판단

- 유의 수준 significant level : 제1 종 오류를 범하는 최대 허용 확률

- 유의 확률 significant probability : 귀무가설이 맞다고 할때 주어진 데이터가 우연히 대립가설을 지지할 확률

t 검정

 - 모집단의 분산을 모를떄, 모집단을 대표하는 표본으로 부터 추정된 분산을 이용하여 t분포에 의존해 검정하는 방법

두 모집단 비교

- 가정

- 공통 분산 sigma2는 합동표본분산 S_p^2(pooled sample variance)로 추정

두 모집단 비교 예제 1

- 약의 생산 후와 1년 후 약효 측정 결과

- mu1, mu2가 생산 직후와 1년후 약의 평균 약효

 => 1년이 지나도 약효가 보존되는지 가설 검정

1) 가설 설정

2) 검정 통계량 구하기

3) 의사결정

- 검정 통계량 3.85가 자유도가 18인 t분포에서 alpha가 0.025인 경우 2.101으로 보다 크다

 => 귀무 가설은 기각

 유의수준 0.05에서 약을 오래 보존하면 달라진다.

4) 신뢰 구간

t 검정 결과

- 유의수준 0.05일떄, 자유도 18, 검정 통계량 t0 = 3.8511

- 유의확률 p value = 0.00117로 0.05보다 훨씬 작으므로 귀무가설 기각

실험 계획을 하는 이유

- 특정 프로세스와 시스템을 이해 -> 최적화 등 의사결정 목적

1. 중요 요인 찾기 : 정화하는데 소요되는 시간에 영향을 미치는 정화수 종류, 온도, 필터 종류 등의 유의성 파악

2. 입력 변수와 출력변수간 관계 파악 : 염색할때 염색 온도가 명암에 미치는 영향 파악

3. 최적 조건 찾기 : 독립변수가 종속 변수에 영향을 미칠때(통계적 유의성이 존재시) 최적 조건을 위함

4. 비교 실험 : 여러 가지 약물의 효과 비교를 위하여 실시

프로세스 모형

연구의 종류

- 관측 연구와 실험 연구

1. 관측 연구

 - 기존의 자료, 관측 등

2. 실험 연구

 - 실험 대상에 대해 처리를 하는 연구

 - 모든 연구는 관측 연구에서 시작하여 실험을 통해 확인

실험 계획 기본 원리

1. 랜덤화 randomization

 - 실험 단위 배정/순서를 임의로 결정

2. 블록화

 - 실험 대상끼리 묶기. 블록화 후 블록 내에서 랜덤화

 ex. 젋은 사람과 나이든 사람에게 약 효과에 차이가 있다.

 -> 젋은 사람/젋지 않은 사람 두 그룹으로 나누어야 한다.

3. 교락 confounding

 - 고차의 교호작용효과와 블록효과 간 분간이 안되는것

  => 실험 계획을 잘못 할 경우 교락이 되어 분리가 안됨. 

4. 직교화 orthogonalization

 - 주효과와 부호의 곱으로 표현되는 열(교효작용)이 균형 (각 요인의 효과가 독립이라고 추정)

실험 계획 예시 1 - 감기에 대한 비타민 C 효과 실험

- 감기 환자들을 임의로 두 그룹으로 나눔

- 한 그룹(실험 집단)에는 비타민 C를 주고, 다른 그룹(대조 집단)에게는 위약을 준다.

- 이중 눈가림 실험 실시(맹검법 double blind test) 실시

=> 맹검법 : 실험자와 피실험자 둘다 정보를 주지않는것.

ref : ko.wikipedia.org/wiki/%EB%A7%B9%EA%B2%80%EB%B2%95

실험 계획 예시 2 - 동물 전염병에 대한 치료제 효과 파악

1. 실험 1 

- 작년에 태어난 동물에게 기존 치료제 투여시 발병률

- 올해에 태어난 동물에게 새 치료제 투여시 발병률

=> 동물 성장 시 환경적 요인이 다르므로 약효도 다를 수 있어 좋지 않음.

2. 실험 2

- 올해 동물을 임의로 그룹을 나눔

- 맹검법 실시

=> 더 낫다.

심슨의 모순

- 전체적으로 본 결론과 세부적으로 나누어본 결론이 다름

- 각 부분에 대한 평균이 크다고 해서 전체에 대한 평균까지 크지는 않다

ex.   어느 대학 신입생 합격률에서 여성 합격률이 낮았음.  단과대 별로 보니 남성이 합격률이 낮음

ref : namu.wiki/w/%EC%8B%AC%EC%8A%A8%EC%9D%98%20%EC%97%AD%EC%84%A4

 => 신입생 합격률 자체는 남성이 높으나 단과별 합격룰은 여성이 더 높음.

실험 계획 순서

1. 문제 발생

2. 목적 설정

3. 반응 변수(특성값) 선정. 

   요인과 수준 선정

   실험 설계 선정

 * 어떤 효과들 끼리 서로 교락이 되서 분리가 안되는 상황을 피하도록 실험을 계획하여야함

4. 실험 수행

5. 자료 분석, 결과 검토

6. 결론, 조치

7. 목적 달성 

8. 문제 해결