평균 검정
- 단일 표본에서 모평균
- 두 독립 표본에서 평균 검정(평균이 같은가 다른가)
- 대응 표본에서 평균 검정
=> t 검정
t검정 t test(평균 검정)
- 모집단의 분산이나 표준편차를 모를때
표본으로 추정된 분산이나 표준편차로 검정.
- 두 모집단에 평균간 차이는 없다 라는 귀무가설과
평균 간 차이가 있다는 귀무가설중 하나를 선택가능한 통계적방법
예습
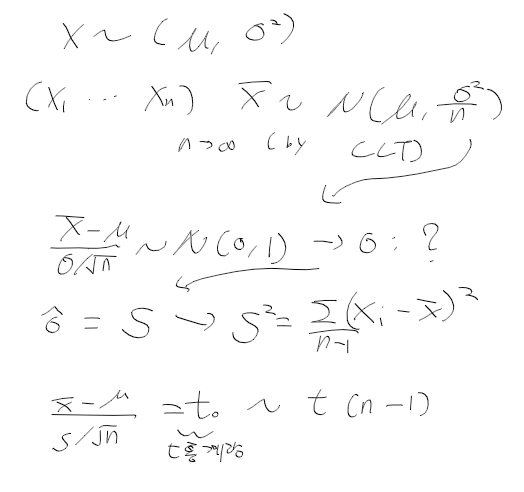
1. 단일 표본 모평균 검정
- 25마리 게 체온을 이용한 단일 표본에서의 모평균 검정
귀무가설 H0 : mu = 24.3 vs 대립가설 H1 : mu != 24.3
1.1 R에서 모평균 검정

t0 = 2.7128
p value = 0.0124 ->
유의수준 alpha = 0.05 이라면
p value < alpha 이므로 귀무가설을 기각한다.

1.2 파이썬에서 모평균 검정
파일 읽기

실수형으로 데이터 변환

t검정
- ttest_1samp(데이터, 모평균)은 [tvalue, pvalue]를 리스트로 반환

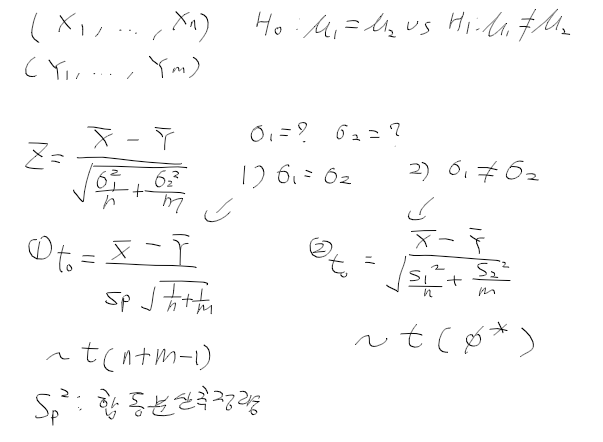
2. 두 독립 표본에서 평균 검정
- 아까는 25마리의 게 체온이었다면 이번에는 두 종류의 지열제 효과 측정
- 13명 참여자 임의 분할. 한 그룹에 지혈제 B, 다른 그룹은 지혈제 G
- 두 독립표본의 평균차이가 존재하는지 검정
귀무 가설 H0 : mu0 = mu1 vs
대립 가설 H1 : mu0 != mu1
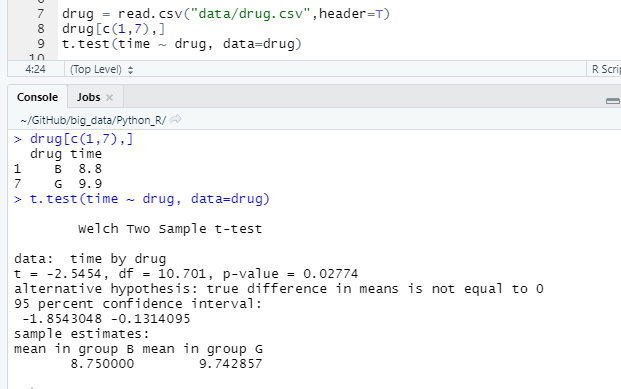
2.1 R에서 t test
t0 = -2.54
df = 10.701
p value = 0.0274 < 유의수준 0.05이므로 귀무가설 기각
=> 두 그룹에서 차이는 존재한다.
분산에 대한 검증 F test
- var.test()함수
p value가 0.4722로 <0.05보다 작다 => 귀무가설 기각
=> 분산이 같다고 보자

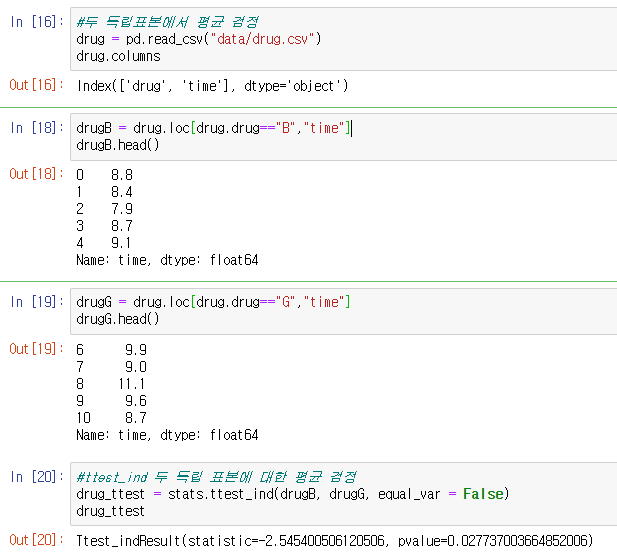
2.2 파이썬에서 ttest
3. 대응된 표본에서의 평균 검정
- 사슴의 왼쪽 뒷다리와 왼쪽 앞다리 길이 데이터. 두 다리 길이가 같은지 다른지 알고싶음
- 한 사슴에서의 다리를 측정하였으므로 대응 표본.
- 대응 표본에서 평균 차이를 검정
H0 : mu1 = mu2 vs H1 : mu1 != mu2

3.1 R에서
t0 = 3.4138
df = n - 1 = 10 - 1 = 9
p value = 0.0077 -> 귀무가설 기각
=> 앞다리 뒤다리 차이 있다.

3.2 파이썬에서 대응 표본의 t검정
n = 10
-> df = n -1 = 9

'수학 > 통계' 카테고리의 다른 글
| 실험계획 - 1. 실험 계획 개념 (0) | 2020.10.29 |
|---|---|
| 파이썬R - 8. 분산 분석 (0) | 2020.10.28 |
| 파이썬R - 6. 파이썬 기술통계 (0) | 2020.10.28 |
| 파이썬R - 5. R 기술통계 (0) | 2020.10.28 |
| 파이썬R - 4. 파이썬과 R 그래픽 라이브러리 (0) | 2020.10.28 |