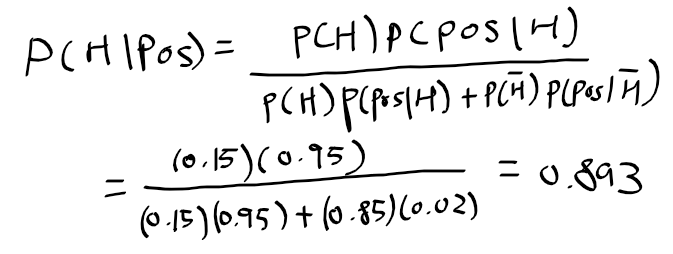집밖은 위험해

수치해석 numerical analysis

- 수치 해석은 연속수학 contiuous mathematics 문제를 해결하기 위한 알고리즘 연구하는 학문

수치 해석의 범위

- 실수 변수나 복소 변수 방정식

- 실수나 복소 평면에서의 수치 선형 대수

- 미분 방정식의 해

- 물리과학과 공학 관련 문제들

수치해석과 알고리즘

- 연속 수학에서 몇몇 문제들은 알고리즘으로 해결 될 수 있음

-> 직접 방법 direct method라고 함

ex. 선형 시스템 방적식 system of linear equation을 풀기하기 위한 가우시안 제거 gaussian elimation와 선형 프로그래밍linear programming에서 단체법 simplex method

* 단체법 simplex method : 선형 계획법에서 선형 계획 문제의 최적해를 구하는 알고리즘

=> 그러나 대부분의 문제에서 직접 방법은 존재하지 않음

수학의 필요성

- 역사적으로 과학의 발달은 논리적 사고 쳬계 확립과 이를 표현하기 위한 기호의 논리에 근간을 두어 기호가 양을 표현할때 수학은 이들 사이의 관계를 이해하는데 필수적.

- 물리, 화학, 생물학 등 자연 과학과 기계, 전자, 전산 등 응용과학 등 모든 분야의 기초 이론에 응용됨

수학의 세부 분류

1. 대수학 algebra

- 가환대수, 표현론, 대수기하학, 결합론, 정수론

2. 기하학 geometry/ 위상수학 topology

- 퍼지수학, 리만 기하학, 엽층이론

3. 해석학 analysis

- 적분론, 편미분장정식, 복소함수론

4. 확률/ 통계학

- 수리 통계학, 화귀분석, 확률론, 확률미방

5. 응용수학/ 수리물리

- 통계역학, 동력학계, 유체역학

6. 이산수학/ 전산수학

- 조합론, 수치해석, 암호론

어떤 환자가 HIV virus가 걸린것으로 의심되면 혈액의 항체를 검사하는 ELISA test를 한다.

H를 HIV virus를 가진 사건으로 $\bar{H}$를 가지지 않은 사건.

Pos를 테스트에서 양성으로 나온 사건, Neg는 음성으로 나온 사건

이 때 test에서 양성으로 나온 환자가 HIV 바이러스를 가질 확률 P(H | pos)를 구하자

이때 아래의 확률을 가정한다

베이즈 정리에 따라 다음과 같이 구할수 있다.

우도 likelihood

- 어떤 가설 hypothesis H에 대한 우도 likelihood란 어떤 시행의 결과 evidence E가 주어질때, 가설 H가 참이라면 결과 E가 나올 정도가 얼마나 되는가

-> 결과 E가 나온 경우, 이 결과가 나올수 있는 여러 가설들을 평가할수 있는 측도가 우도

베이즈 정리와 우도

- 전문가 시스템의 불확실성을 평가하기 위해 베이즈 정리가 사용

- 사전 확률에 새로운 증거를 대입하여 사후확률을 얻으나 사전 확률 부여에 자의성을 배제하기 어려움

-> 우도를 사용하여 자의성을 벗어나 용이하게 사전확률 계산이 가능

최대 우도의 원리 principle of maximum likelihood

- 어떤 가설에 대한 우도를 주어진 데이터가 그 가설을 지지하는 정도로 해석한다면

 -> 우도가 최대가 되는 가설을 선호하게 됨.

- 그 가설이 어떤 모집단의 모수 population parameter에 관한 가설이라면, 그 추정치를 해당 모집단에서 가장 적절한 추정치로서 선호할 수 있음

=> 어떤 모수에 관한 가장 적절한 추정치 estimate를 구하는 방법을 최대 우도 방법 method of maximum likelihood이라 함.

나이브 베이지안 분류 naive bayesian classification

- naive basyesian classification은 일명 idiot's bayes, idot라는 의미를 가지며, 단순 확률적 분류법이다.

- 더 정확한 묘사는 independent feature model

- 실제로 생길수 없는 강한 독립 가정을 포함하여 naive(순진한, 고지식한)라는 말을 사용

나이브 베이지안 분류의 활용

- 확률 모델의 정밀성으로 나이브 베이즈 분류기는 지도학습에서 효율적으로 훈련됨.

- 나이브 베이즈 모델을 위한 인수 추정은 최대 우도법을 사용

=> 베이지안 확률이나 다른 베이지안 방법대신 나이브 베이지안 모델로 작업 가능

베이지안 네트워크 bayseian network

- 믿음 네트워크 belief network, 인과 네트워크 caual network는 다 같은 의미

- 베이지안 네트워크는 변수를 표현하는 노드와 변수간 의존관계를 포현하는 호의 방향성 비순환 그래프 directed acycle graph

부모 노드

- 노드 A에서 노드 B까지 호가 있는 경우

-> A는 B의 부모 노드

증거 노드 evidence node

- 노드에 값이 주어진 경우

노드

- 측정값, 인수, 숨겨진 latent 변수, 가설 등 어떤 종류의 변수로 제약이 없음

베이지안 네트워크와 확률 분포

- 그래프 상에 노드에 의해 표현되는 모든 변수에 대한 결합 확률 분포 joint distribution

- 변수 : X(1), ... X(n)

- parants(A)는 노드 A의 부모라 하자.

=> X(n)을 통한 X(1)의 결합확률분포는 i가 1부터 n까지일떄, 확률분포 p(X(i) | parents(X(i))의 곱으로 표현

-> X가 부모를 갖지 않는 경우 이 확률분포는 비조건부 unconditional이며, 부모가 있는 경우 조건부 conditional이 된다.

베이지안 네트워크 활용

- 의약

- 엔지니어

- 텍스트 분석

- 이미지 처리

- 결정 제안 시스템

베이즈 정리 bayes theorem

- 조건부 확률에서 새 정보를 알았을때 확률의 개선이 일어남

-> 실험 결과로 나온 정보로 어느 사건의 처음 확률이 개선 가능

- 처음 확률을 사전 확률 prior probability, 개선된 확률 posterior probabililty

-> 확률의 개선을 베이즈정리라 함.

확률 이론

- 고전적 이론 classical theory

- 선험적 이론 priori theory

- 상대빈도 이론 relative frequency theory

- 주관주의 이론 subjectivist theory

확률과 통계학의 응용

- 인공지능 분야에서 불확실한 지식의 표현과 처리에 활용

- 전문가 시스템 중에 초기 시스템에 해당되는 prospector와 mycin은 각각 베이지안 확률과 확신도 certainty factor 이용

- 많은 시스템들이 zadeh의 퍼지 이론, dempster의 증거 이론 theory of evidence 등을 사용하여 불확실성 문제를 다룸

베이지안 확률 bayesian probability

- 베이즈주의 bayesianism, 주관주의 subjectivism, 개인적 확률 personal probability, 인식론적 확률 epistemic probability 모두 같은 의미

- 베이즈 주의는 수학적 확률 이론이 가능성의 정도 degree of plausibility나 진실 여부에 대한 믿음의 정도 degree of belief에 적용되는 철학적 주의 tenet

- 베이즈 주의가 베이즈 정리 bayes theorem과 함께 사용하면 베이즈 추론이 됨.

- 빈도주의와 대조되는 개념

빈도주의 frequentism

- 수학적 확률을 개인의 믿음 정도로 해석하는것이 아니라 임의의 사건에 대해 오직 그 상대적 발생 빈도에 따라 확률을 부여

확률의 베이지안적 해석

- 임의의 사건 random events 뿐만 아니라 어떤 종류의 문제 any other kind of statement에도 확률을 부여 가능

빈도주의자 frequentist와 베이즈주의자 bayesian 비교

- 동전 던지기 시 둘다 1/2 확률을 부여 할수 있음.

- 10억년전 화성에 생명체가 있었다라는 명제가 제시

-> 빈도주의자는 상대적인 빈도 frequency에 대해 확률을 줄수는 없으나

-> 베이즈주의자는 개인적인 믿음으로 확률 1/1000을 부여 가능

주관주의 확률 이론에 따른 확률

- 어떤 사람이 특정 순간에 주어진 명제나 사건에 대해 갖는 믿음의 정도 degree of belief

토마스 베이즈

- 영국의 수학자, 장로로서 베이즈 정리 bayes theorem이라는 확률 이론을 형식화 한것으로 유명해짐

forward probability

- 특정 조건의 상황에서 어떤 사건의 황률

ex. 항아리 속에 일정한 개수의 흰돌과 검은돌이 주어질때 검은돌을 꺼낼 확률?

-> 반대의 경우, 하나또는 여러개의 돌을 꺼낸 결과를 보고, 항아리 속에 흰돌과 검은돌의 수는 어떻게 알수있을까?

베이즈 확률 bayesian probability

- 단지 어느 임의의 변수 random variable을 포함하는것이 아니라 어떤 종류의 확률의 응용에서 흔하게 가지는 확률 해석과 관련되어 주어진 이름