집밖은 위험해

상태공간 트리

백트래킹

한정분기

A*알고리즘

상태공간 트리

1. 상태공간 트리의 개요

2. 상태공간 트리를 이용한 여행자 문제 풀이

상태 공간 트리 state-space tree

- 문제 해결 과정 중간 상태를 각각 한 노드로 나타낸 트리

- 세 가지 상태 공간 탐색 기법

 1. 백 트래킹

 2. 한정 분기

 3. A*알고리즘

상태공간 트리를 이용한 여행자 문제 풀이

- 그래프에서 모든 정점을 순회하고 돌아오는 싸이클을 해밀토니안 싸이클이라고 함

- 완전 그래프에서 해밀토니안 싸이클은 수 없이 많은데 여행자 문제는 그 중 가장 짧은 것을 찾는 문제

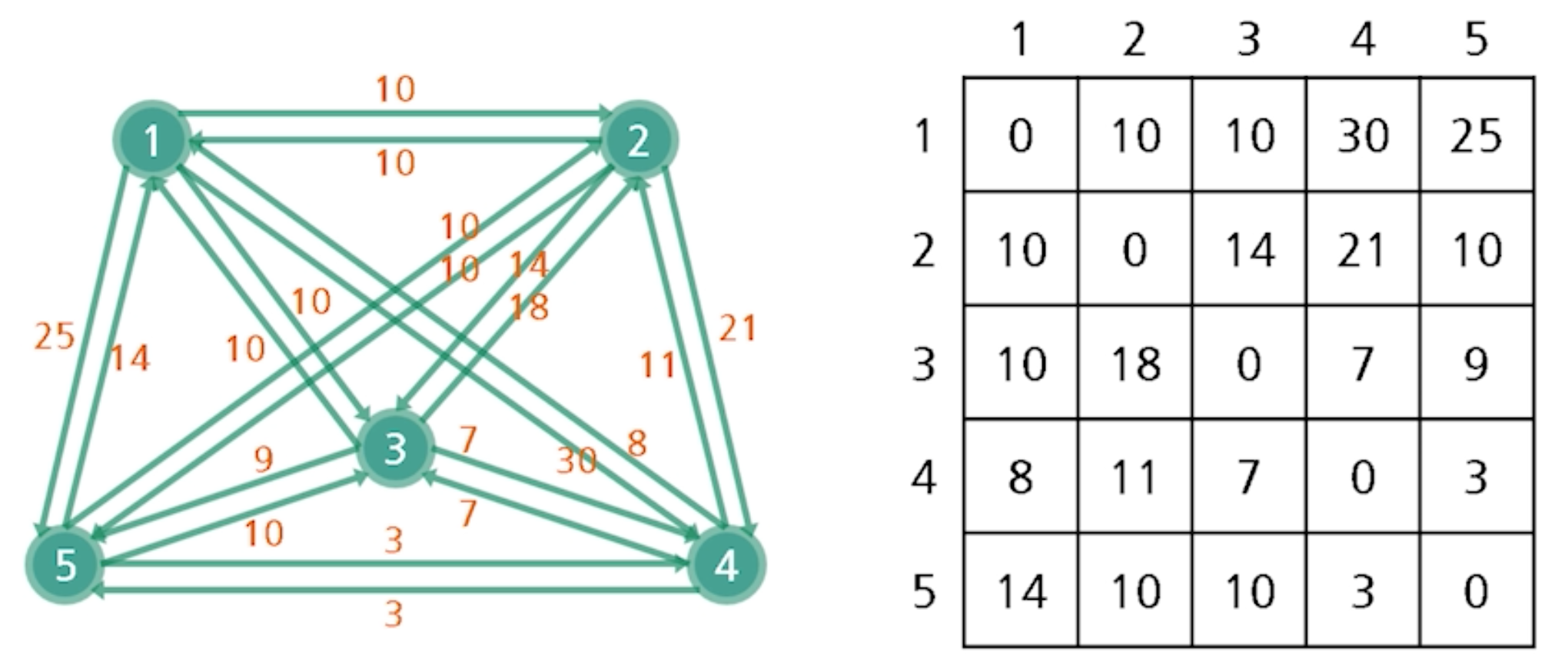
TSP와 인접행렬의 예

사전식 탐색의 상태공간 트리

- 다섯 개의 도시를 가진 TSP의 최적해를 찾으려면 -> 모두 4!(24)개의 해를 검사해보아야함

백트래킹

- DFS 또는 그와 유사한 스타일의 탐색을 총칭. 가능한 지점까지 탐색하다 막히면 되돌아감. 주로 재귀적으로 ㄱ현

- ex : 미로 찾기 문제, 8퀸 문제, 색칠 문제(map coloring)

미로찾기 문제

- S : 시작점

- T : 목표지점

- S에서 시작하여 T까지 이동하는 경로 찾기

미로찾기 문제의 탐색 과정을 상태 공간 트리로 표현하는 방법

1. S에서 시작해 정점 1로 이동, 정점 2 또는 정점 3중 하나를 선택함

2. 임의의 정점 2를 선택함, 막다른 골목에 다다름

3. 정점 2로 오기위해 거쳤던 정점 1로 되돌아감 정점 3으로 감

4. 정점 3으로 이동함, 정점 4와 정점 5중 하나를 선택함

5. 정점 5에 이름, 정점 6과 정점 7중 하나를 선택함

6. 정점 6에 이름, 막다른 골목에 다다름

7. 정점 6으로 오기위해 거쳤던 정첨 5로 되돌아감

8. 정점 7에 이름, 정점 8과 정점 T중 하나를 선택

미로찾기 문제 해결방법 유사코드

mave(v)
{
   visited[v] <- YES;
   if (v = T) then {print "성공!"; exit();}
   for each x in L(v)        L(v) : 정점 v의 인접 정접 집합
       if (visited[x] = NO) then{
           prev[x] <- v;
           maze(x);
       }
}

한정 분기 branch & bound

- 분기와 한정의 결합 -> 분기를 한정시켜 쓸데없는 시간 낭비를 줄이는 방법

- 기존의 상태공간트리에서 사전식 탐색시 (n - 1) ! 시간이 소요됨 => 지수시간 이상 

백트래킹과 공톰정과 차이점

- 공통점 : 경우들을 차례로 나열하는 방법이 필요함

- 차이점 

   백트래킹 : 가보고 더이상 진행되지않으면 되돌아옴

   한정분기 : 최적해를 찾을 가능성이 없으면 분기하지 않음

    -> 지금까지 얻은해보다 더 좋은해가 아니라면 분기를 하지 않음

가지치기의 원리

TSP 예제를 대상으로 한 한정분기 탐색의 예시

A* 알고리즘

1. A*알고리즘 개요

2. 최단 경로 문제

3. A*알고리즘 작동예

4. TSP 예쩨를 대상으로 한 A* 알고리즘 탐색의 예

최적 우선 탐색 BFS Best First Search

- 각 정점이 매력 함숫값 g(x)를 가짐.

- 방문하지 않은 정점들 중 g(x)값이 가장 매력적인 것부터 방법

A* 알고리즘

- 최적 우선 탐색을 이용하여 목적점까지 이르는 잔여 추정 거리를 고려하는 알고리즘

- 정점 x로부터 목적점에 이르는 잔여거리의 추정치 h(x)는 실제치보다 크면 안됨

Remind : 다익스트라 알고리즘

- 시작점은 하나

- 시작점으로부터 다른 모든 정점에 이르는 최단 경로를 구함 -> 목적점이 하나가 아님

<-> A* 알고리즘에서는 목적점이 하나임

다익스트라 알고리즘으로 최단경로 찾기

A*알고리즘을 이용한 최단 경로 찾기

- 추정 잔여거리 h(x): 각 정점에서 목적지 까지 직선 거리

- 시작점을 0, 모든 정점을 무한대로 초기화

- 시작점 주위의 거리 값을 구하고 g(x)라 함.

- g(x) + h(x)하여 우측 그림과 나타낼 수 있음

=> 이 중에서 g(x) + h(x)가 가장 작은 정점 23을 포함시킴

- 정점 41의 g(x) + h(x)값이 60으로 가장 작으므로 포함시킴

=> 추정 잔여거리를 사용하여 탐색의 단계가 현저히 줄어들음

TSP 예제를 대상으로 한 A* 알고리즘 탐색의 예

- 상태 공간 트리

- A* 알고리즘이 첫 리프 노드를 방문하는 순간 종료되는 이유

* 방금 본 그래프는 모든 정점에 대해서 h(x) 값을 미리 계산해둠. 일반적인 상태 공간 트리 문제에서는 미리 주어지지 않고 만들어지면서 탐색이 진행됨 -> 따라서 각 노드에서 목적점에 이르는 길이의 추정치는 그 때 그 때 계산하여야함

상태공간 트리

- 모든 정점을 지나서 시작정점으로 돌아오는지. 가중치의 합이 최소가 되는지 알아봄

- 하한선 33은 모든 정점에서 가장 작게 나가는 값들의 합(1 : 10, 2: 10, 3: 7, 4: 3, 5 : 3 -> 10 + 10 + 7 + 3 + 3 = 33)

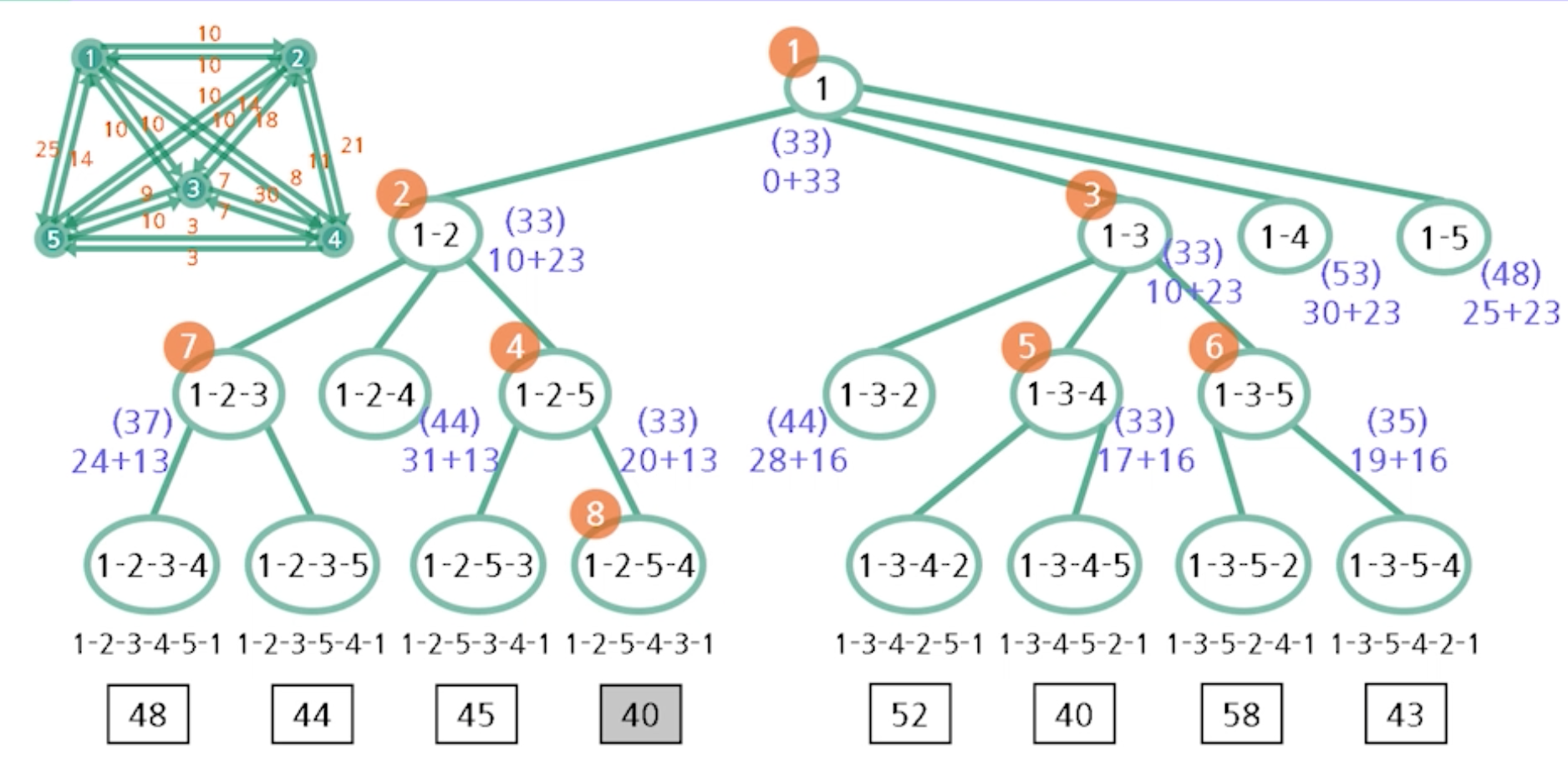
A* 알고리즘이 첫 리프 노드를 방문하느 순간 종료되는 이유

- 계산되지 않은 리프 노드들은 조상 노드의 추정치가 큰편이라 종료 된 것들임

근사 알고리즘

1. 근사 알고리즘이란?

2. 근사 알고리즘과 근사 비율

NP-완비 문제

1. 다항식 시간에 해결할 수 있는 알고리즘이 아직 발견되지 않음

2. 아직까지 누구도 이 문제들을 다항식 시간에 해결할 수 없다는 것을 증명하지 못함

NP-완비 문제를 해결하기 위해 다음 세가지 중 한가지는 포기해야함

1. 다항식 시간에 해를 찾는 것

2. 모든 입력에 대해 해를 찾는것

 - 대부분 입력(즉, 최악의 경우가 아닌 입력)에 대해 최적해를 구하는 다항식 알고리즘 개발

3. 최적해를 찾는 것

 - 최적의 답은 아니더라도 최적에 가까운 준 최적해를 구하는 다항식 알고리즘 개발

근사 알고리즘

- 최적해를 찾는 것을 포기하여 최적해에 근사한 해를 찾음

P : 문제, I : 입력 크기가 n인 P의 한 사례

- V^* (I) : I에 대한 최적해의 값

- V(I) : 근사 알고리즘이 생성한 근사해의 값

근사 비율

- 근사 비율 r(I) : 근사해의 값과 최적해의 값의 비율

- 최대화 문제 : 0 < V(I) <= V^* (I)

- 최소화 문제 : 0 < V^* (I) <= V(I)

크기가 n인 모든 I에 대해 r(I) <= r(n)이면, 근사 알고리즘은 비율 한계가 r(n)임

- r(n) >= 1

- 근사 비율 r(n)이 1이면 최적 알고리즘, 큰 값일 수록 부정확한 해를 산출하는 경우

상대 오차

- 상대 오차의 한계 epsilon(n)

- 모든 I에 대해서 epsilon(I) <= epsilon(n)

- epsilon(n) = 0 -> 최적 알고리즘

근사 알고리즘의 예

1. 여행자 문제

2. 정점 커버 문제

3. 작업 스케줄링 문제

4. 클러스터링 문제

여행자 문제

- 여행자가 임의의 한 도시에서 출발하여 다른 모든 도시를 한 번씩만 방문하고 다시 출발했던 도시로 돌아오는 여행 경로의 거리를 최소화 하는 문제

TSP를 위한 근사 알고리즘 고안

- 다항식 시간 알고리즘을 가지며, 유사한 특성을 가진 문제를 찾아 활용

 -> 최소 싱장 트리 문제 : 모든 점을 사이클 없이 연결하는 트리 중에 트리 선분의 가중치의 합이 최소인 트리

 -> 최소 신장 트리의 모든 점을 연결하는 특성과 최소 가중치의 특성을 응용하여, 시작 도시를 제외한 다른 모든 도시를 트리 선분을 따라 한번 씩 방문하도록 경로를 찾음

여행자 문제의 근사 알고리즘의 예

1. (a) 그래프 G에서 크루스칼 알고리즘이나 프림 알고리즘으로 최소 신장트리 (b)를 구함

2. 도시 1에서 출발하여 트리 선분을따라서 모든 도시를 방문하고 돌아오는 도시의 방문 순서를 (c)와 같이 구함. 방문 순서는 [1 2 4 3 4 5 4 6 7 6 4 2 1]임

3. 순서를 따라서 도시를 방문하되 중복 방문하는 도시를 순서에서 제거하여 여행자 문제의 근사해를 구함. 단 도시 순서의 가장 마지막에 있는 출발 도시 1은 중복되어 나타나지만 제거하지 않음

유사 코드

- 입력 : n개의 도시, 각 도시간의 거리

- 출력 : 출발 도시에서 각 도시를 한 번씩만 방문하고 출발 도시로 돌아오는 도시 순서

1. 입력에 대해 MST를 찾음

2. MST에서 임의의 도시로부터 출발하여 트리의 선분을 따라 모든 도시를 방문하고 다시 출발했던 도시로 돌아오는 도시 방문 순서를 찾음

3. return 이전 단계에서 찾은 도시 순서에서 중복되어 나타나는 도시를 제거한 도시 순서(단, 도시 순서의 가장 마지막의 출발 도시는 제거하지 않음)

-> 시간 복잡도는(크루스칼이나 프림 알고리즘의 시간 복잡도) + O(n) + O(n)이므로 크루스칼이나 프림 알고리즘의 시간 복잡도와 같음

근사 비율

- 여행자 문제의 최적해를 알 수 없ㅇ므로, '간접적인' 최적해인 최소 신장 트리 선분의 가중치 합 M을 최적해의 값으로 활용

- 실제 최적해의 값이 M보다 항상 크기 때문

- Approx_MST_TSP 알고리즘이 계산한 근사해의 값은 2보다 크지 않음

 -> MST의 선분을 따라서 도시 방문 순서를 찾을 때 사용된 트리 선분을 살펴보면, 각 선분이 두 번 사용됨

 -> 따라서 이 도시 방문 순서에 따른 경로의 총 길이는 2M임

 -> 삼각 부등식의 원리를 이용하여 새로운 도시 방문 순서를 만들기 때문에, 이전 도시 방문순서에 따 경로 길이보다 새로운 도시 방문 순서에 따른 경로의 길이가 더 짧음

정점 커버 문제 vertex cover problem

- 주어진 그래프 G = (V, E)에서 각 선분의 양 끝점들 중에서 적어도 하나의 끝 점을 포함하는 점들의 집합 중에서 최소 크기의 집합을 찾는 문제

- 정점 커버를 살펴보면, 그래프의 모든 선분이 정점 커버에 속한 점에 인접해 있음. 즉, 정점 커버에 속한 점으로서 그래프의 모든 선분을 커버하는 것

정점 커버 문제의 예 1

- 그래프 G에서 {1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}이 각각 정점 커버

- {2}또는 {3}은 정점 커버가 아님. {2}는 선분 (1, 3)을 거버하지 못하고, {3}은 선분 (1, 2)를 커버하지 못함

- 그래프에 대한 정점 커버 문제의 해는 {1}이 됨

정점 커버 문제의 예 2

1. 아래의 그래프 G는 어느 건물의 내부 도면을 나타냄

- 건물의 모든 복도를 감시하기 위해 가장 적은수의 CCTV 카메라를 설치하고자 함

- 이를 위해서 3대의 카메라를 각각 점 1, 5, 6에 설치하면 모든 복도(선분)를 '커버'할 수 있음

정점 커버 문제의 두가지 접근 방법

1. 먼저 차수가 가장 높은 점을 우선 선택하면 많은 수의 선분이 커버 됨

2. 점을 선택하는 대신에 선분을 선택하는 것

- 선분을 선택하면 선택된 선분의 양 끝점에 인접한 선분이 모두 커버됨

- 따라서 정컴 커버는 선택된 각 선분의 양 끝점들의 집합임

- 정점 커버를 만들어 가는 과정에서, 새 선분은 자신의 양 끝점들이 이미 선택된 선분의 양 끝점들의 집합에 포함되지 않을 때에만 선택됨

작업 스캐줄링 문제

- n개의 작업, 각 작업 수행시간 t_i, i = 1, 2, 3, ..., n 그리고 m개의 동일한 기계가 주어질 때, 모든 작업이 가장 빨리 종료되도록 작업글 기계에 배정하는 문제

작업 스케줄링 문제의 조건

- 한 작업은 배정된 기계에서 연속적으로 수행되어야 함

- 기계는 한 번에 하나의 작업만을 수행함

가장 간단한 해법은 그리디 방법으로 작업 배정

- 현재까지 배정된 작업에 대해 가장 빨리 끝나는 기계에 새 작업을 배정하는 것

작업 스케줄링 문제를 그리디 알고리즘을 이용하여 근사해를 구하는 유사 코드

Approx_JobScheduling
입력 : n개의 작업, 각 작업 수행 시간 t_i, i = 1, 2, ..., n 기계 M_j, j = 1, 2, ..., m
출력 : 모든 작업이 종료된 시간
for j = 1 to m
   L[j] = 0             L[j] = 기계 M_j에 배정된 마지막 작업의 종료 시간
for i = 1 to n {
   min = 1
   for j = 2 to m {                      가장 일찍 끝나는 기계를 찾음
       if (L[j] < L[min])
           min = j
   }
   작업 i를 기계 M_min에 배정함
   L[min] = L[min] + t_i
}

return 가장 늦은 작업 종료 시간

작업 스케줄링 문제 해법의 작동 예

- 작업 수행 시간 : 5, 2, 4, 3, 4, 7, 9, 2, 4, 1

- 기계 : 4개

시간 복잡도

1. approx_jobscheduling 알고리즘은 n개의 작업을 하나씩 가장 빨리 끝나는 기계에 배정함

- 이러한 기계를 찾기 위해 알고리즘의 for루프가 m-1번 수행됨

- 모든 기계의 마지막 작업 종료 시간인 L[j]를 살펴봐야하므로 O(m) 시간이 소요됨

2. 시간 복잡도 n개의 작업을 배정해야하고, 배열 L을 탐색해야 하므로 n x O(m) + O(m) = O(nm)임

근사 비율

1. approx_jobscheduling 알고리즘의 근사해를 opt'라 하고, 최적해를 Opt라고 할 때 ,opt' <= 2 x opt임

2. 근사해는 최적해의 두 배를 넘지 않음. t_i는 작업 i의 수행 시간임.

3. 가장 마지막으로 배정된 작업 i가 T부터 수행되며, 모든 작업이 T + T_i에 종료된 것을 보이고 있음. 그러므로 OTP' = T + t_i임.

4. T'는 작업 i를 제외한 모든 작업의 수행 시간의 합을 기계의 수 m으로 나눈 값임. T'는 작업 i를 제외한 i를 평균 종료 시간임

5. T <= T'이 됨

 - 작업 i가 배정된(가장 늦게 끝나는) 기계를 제외한 모든 기계에 배정된 작업은 적어도 T 이후에 종료되기 때문임.

클러스터링 문제

- n개의 점이 2차원 평면에 주어질 때, 이 점들 간의 거리를 고려하여 k개의 그룹으로 나누고자 하는 문제

클러스터링 문제 조건

- 입력으로 주어진 n개의 점을 k개의 그룹으로 나누고 각 그룹의 중심이 되는 k개의 점을 선택하는 문제임

- 단, 가장 큰 반경을 가진 그룹의 직경이 최소가 되도록 k개의 점이 선택되어야 함

클러스터링 문제 해결 전략

1. n개의 점 중에서 k개의 센터를 선택해야 하는데, 이를 한 꺼번에 선택하는 것 보다 한 개씩 선택하는 것이 쉬움

2. 오른쪽 그립 같이 첫 번째 센터가 랜덤하게 정해졌다고 가정함

3. 두 번째 센터는 두 개의 센터가 서로 가까이 있는 것보다 멀리 떨어져 있는 것이 좋음

4. 다음 세 번째 센터는 첫 번째와 두 번째 센터에서 가장 멀리 떨어진 점을 선택

NP-완비(NP-Complete)군

- 지금까지 기술로 다항식 시간에 풀기 어렵다고 판단되면서 서로 밀접한 논리적 연결관계를 가진 문제들의 집합

-> 한 문제가 다항식 시간에 해결 가능하다면, 다른 문제의 답도 말해줄수 있는 경우 이 군에 속하는 모든 문제가 다항식 시간에 풀림

NP-완비임을 증명하는 것에 대한 의미

1. 어떤 최적화 문제를 햏결하는 효율적인 알고리즘을 찾을 수 있을 때

2. 이 문제의 yes/no 버전의 문제가 np-완비 임이 증면되면 이 문제군의 단 한문제에 대해서도 효율적인 알고리즘을 발견하지 못했음을 알 수 있음

NP-완비 이론의 상황을 비유적 예시

상사가 아주 어려운 문제를 해결하라고 지시

- 문제가 어렵다는 것을 상사에게 설득하는 세 가지 방법

1. 나는 답을 구할 수가 없습니다. 아마 나는 멍청한 모양입니다.

2. 나는 답을 구할 수가 없습니다. 왜냐하면 이 문제는 답이 없어요.

3. 나는 답을 구할 수가 없습니다. 그렇지만 저렇게 수많은 천재들도 이 문제를 해결할 수 없습니다

 -> NP-완비 이론의 상황을 비유적으로 보여줌

=> 상사가 준 문제를 NP 완비임을 안다면 수많은 천재들도 풀지못한 어려운 문제에 속함을 알 수 있음

NP-완비의 정의

- 문제 A가 다음의 두 조건을 만족하면 NP-완비임

-> A는 NP이다

-> A는 NP-Hard 이다.

NP-하드의 정의

- 문제 A가 다음 성질을 만족하면 NP-하드임

-> 알려진 임의의 NP-하드 문제 L로부터 문제 A로 다항식 시간에 변환 가능하다.

-> 모든 NP 문제가 L에 대해 L <=_p A이다.

=> 만일 문제 A를 쉽게 풀수 있다면, 문제 L도 쉽게 풀 수 있음 => 그러므로 모든 NP 문제를 쉽게 풀 수 있음

NP-완비 문제들

문제의 종류

1. 문제의 종류란

2. 현실적인 시간의 문제

3. 결정 문제와 최적화 문제

문제의 종료

해결 가능성 여부

- 풀수 없는 문제들

 현실적인 시간에 풀수 없는 문제들 -> 주어진 시간 범위에서 근사해를 구하는것이 목표

- 풀수 있는 문제들

 현실적인 시간에 풀수 있는 문제들 -> 지금까지 배운 문제들

풀수 없는 문제 unsolvable/undecidable

- 정지 문제

- 힐베리트의 10번째 문제

풀수 있는 문제 solvable/decidable

- 최소 신장 트리 문제, 최단 거리 문제(현실적인 시간 내에 풀수 있는 문제)

- Presburge 산술, NP-완비 (현실적인 시간 내 풀수 없는 문제)

현실적인 시간의 의미

- 다항식 시간의 의미 : 입력 크기가 n일경우 그 문제를 해결하는데 n의 다항식에 비례하는 시간이 걸릴 경우

  ex. 3 n ^ k + 5 n ^(k-1) + ..., n^k log n

- 비다항식 시간의 예시

 지수 시간 - ex : 2^n

 계승 시간 - ex : n!

요구하는 대답의 종류에 따른 문제 분류

- 결정 문제(판정문제) : yes or no의 대답을 요구하는 문제

- 최적화 문제 : 가장 좋은 해를 요구하는 문제

ex. 최단 거리 문제의 경우

- 결정 문제 : 정점 u에서 정점 v로 가는 길이 100이하인 경로가 존재하는가?

- 최적화 문제 : 정점 u에서 정점 v로 가는 최단 경로의 길이는 얼마인가?

NP-완비 이론의 전개를 쉽게하기 위해 yes/no(결정 문제)만을 대상으로 함

- 최적화 문제 -> 결정 문제로 바꿈

- 최적화 문제는 결정 문제보다 대답이 쉽지 않으므로 결정 문제가 어렵다면 최적화 문제도 어렵다고 할 수 있음

ex. TSP 문제 (Traveling Sales man Problem)

- n 개의 도시를 모두 방문하고 돌아오는 최단 거리를 구하라 (최적화 문제)

=> n개의 도시를 모두 방문하고 돌아오는 거리 K이하인 경로가 존재하는가? (결정 문제)

YES/No 문제는 다른말로 결정 문제(Decision Problem)라고 불림

- 어떤 문제를 다항식 시간에 결정 할 수 있으면 현실적인 시간에 풀 수 있음 (Tractable)

- 다항식 시간에 결정할 수 없으면 현실적인 시간에 풀 수 없음 (Intractable)

NP-완비(NP-Complete)

1. 다항식 시간에 해결할 수 있는 알고리즘은 발견된 바 없음

2. 다항식 시간에 해결 불가능하다고 증명된 것도 아님

3. 수천 수만의 NP-완비 문제중 단 하나라도 다항시간에 해결되면 모든 NP-완비 문제가 한번에 다항식 시간에 해결되는 논리적 연결 체계를 가지고 있음

NP군의 의미(NP : Nondeterministric Polynomial)

P 문제

- P : 다항식 시간에 해결할 수 있는 문제들의 군

- 지금까지 배운 문제는 모두 P 군

- 다항식 시간 내에서 더 적은 시간을 소요하는 알고리즘을 개발하는데 초점이 맞추어져 있음

NP 문제

- NP : 다항식 시간에 해결할 수 없는 문제군(Non-Polynomial)이 아님

- Nondeterministric Polynomial -> 비결정론적 다항식 시간에 해결할 수 있는 문제군

P와 NP의 가능한 두가지 포함 관계

- 모든 P군의 문제는 NP군에 속함

- P = NP ? NP - P = 공집합?

비결정론적 다항식 시간의 의미

- 임의의 그래프와 두 정점 S, F가 주어질 때, 정점 S에서 출발해서 정점 F에 이르는 경로가 존재하는지 알아보는 알고리즘을 개발하려는 경우

- 어디로가야 유리한지에 대한 정보가 없는 경우 최악의 경우 각 정점에서 두가지 씩 시도해 보아야 함

- 간선을 하나 따라가 보는 것을 1만큼 든다고 하는 경우

 -> 결정론적으로 말하면 최악의 경우 6의 시간 소요, 비결정론으로 말하면 2의 시간이 소요

=> 답을 구하는 과정에 시행착오는 고려하지 않고 그런 경로가 존재한다면 그 경로를 따라 F에 이르는데 걸리는 시간을 을 의미

변환

- 의미 : 변환(Reduction)은 NP-완비 이론의 논리 체계를 구성하는 핵심 원리

- 가정 결정문제 A가 다항식 시간에 해결가능한지를 알고 싶은데, 다항식 시간에 해결가능한 결정 문제 B를 이미 알고있다고 가정함

다항식 시간 변환

- 문제 A의 사례 alpha를 문제 B의 사례 beta로 바꾸되 아래의 성질을 만족하면 Polynomial - Time Reduction 이라 하고, 이를 alpha <=_p beta로 표기함

1. 변환은 다항식 시간에 이루어짐

2. 두 사례의 답은 일치함

문제 A를 푸는 알고리즘

1. 문제 A의 사례 alpha를 다항식 시간에 문제 B의 사례 beta로 변환

2. 변환된 사례 beta를 문제 B를 푸는 알고리즘을 이용하여 품

3. 사례 beta의 답이 yes이면 사례 alpha의 답은 yes, No이면 사례 alpha의 답은 no

=> 문제 B가 쉬운 문제라면 문제 A도 쉬운 문제임

변환의 예

해밀토니안 싸이클 Hamiltonian Cycle

- 그래프의 모든 정점을 한번씩만 방문하고 출발점으로 돌아오는 경로

- 입력 : 무방향 그래프 G = (V, E)

- 질문 : G에 해밀토니안 싸이클이 존재하는가? => 결정 문제

순회 세일즈맨 문제, 여행자 문제(Trabeling Salesman Problem : TSP)

- 가중치 있는 완전 그래프에서 길이가 가장 짧은 해밀토니안 싸이클의 길이를 찾는 문제

- 입력 : 양의 가중치를 갖는 무방향 완전 그래프 G = (V, E), 양의 실수 K

- 질문 : G에 길이가 K이하인 해밀토니안 싸이클이 존재하는가? => 결정 문제

1. 해밀토니안 싸이클 문제의 instance(사례) alpha를 아래와 같이 TSP 문제의 instance beta로 다항식 시간에 변환함

1. 사례 alpha가 해밀토니안 싸이클을 가짐

2. 사례 beta가 길이 4이하인 해밀토니안 싸이클을 가짐(그래프의 크기가 n이면 4대신 n)

최단 경로 shortest path

최단 경로 조건

- 간선 가중치가 있는 유향 그래프

- 무향 그래프는 각 간선에 대해 유향 간선이 있는 유향 그래프로 생각할 수 있음

 -> 무향 간선 [u, v]는 유향 간선 [u,v]와 [v, u]가 존재한다고 가정하면 됨

두 정점 사이의 최단 경로

- 두 정점 사이의 경로들 중 간선의 가중치 합이 최소인 경로

- 간선 가중치의 합이 음인 싸이클이 있으면 문제가 정의되지 않음

단일 시작점 최단 경로

- 단일 시작점으로부터 각 정점에 이르는 최단 경로를 구함

- 다익스트라 알고리즘 : 음의 가중치를 허용하지 않는 최단경로

- 벨만 포드 알고리즘 : 음의 가중치를 허용하는 최단 경로

- 싸이클이 없는 그래프의 최단 경로

모든 쌍 최단 경로

- 모든 정점쌍 사이의 최단 경로를 모두 구함

- 플로이드-워샬 알고리즘

다익스트라 알고리즘

다익스트라 알고리즘 개요

- 음의 가중치가 없는 그래프에서 한 노드에서 다른 모든노드까지의 최단 거리를 구하는 알고리즘

- 에츠허르 데이크스타라 라는 네덜란드 출신의 컴퓨터 과학자에 의해 고안됨

다익스트라 알고리즘 예제

1. 시작정점 r만 최단거리 0으로 초기화하고 다른 정점들의 최단거리는 모두 무한대로 초기화함

2. 정점 r을 집합 S의 첫 번째 워소로 포함 시킴

3. 정점 r에 연결된 집합 S 바깥의 정점들을 살핌

4. 정점 r에서 바깥 정점들에 이르는 거리를 각 정점에 기록함

- 집합 S는 정점 r만으로 구성되어있음

- r에서 정점에 이르는 거리는 각 '8', ''9', '11'임

- 정점에서 기록돈 값은 시작 정점 r에서 해당 정점에 이르는 현재까지의 최단 거리임

- 연결된 세 정점 각각 '8', '9', '11'의 최단 거리값을 가짐

- 나머지 정점들은 모두 무한대의 최단거리 값을 가짐

5. 계산되어 있는 최단거리가 가장 짧은 정점을 집합 S에 포함시킴

- 집합 S의 바깥 정점들 중 최단 거리값이 가장 낮은 것은 '8'임

- 가장 짧은 정점 '8'을 집합 S에 포함시키고 나니 한 정점의 최단 거리 값이 무한대에서 '18'로 바뀜

- 집합 S 바깥 정점들 중 최단거리 값이 가장 낮은 것은 '9'임

6. 연결 비용이 '9'인 정점을 집합 S에 포함시킴

- 최단거리 '18'이던 정점의 최단거리가 '10'으로 바뀜

 -> 정점의 최단 거리가 무한대가 아닌 수에서 바뀌는 이유 : 기존 경로보다 더 짧은 경로가 발견된 경우

 -> 정점의 최단 거리는 여러번 바뀔 수 있음

- 나머지 정점들 중 최단 거리 값이 가장 낮은 것은 '10'임

7. 연결 비용이 '10'인 정점을 집합 S에 포함시킴

- 가장 짧은 정점 '10'을 집합 S에 포함시키고 나니 한 정점의 최단거리값이 무한대에서 '12'로 바뀜

8. 최단거리 '11'인 정점이 집합 S에 추가됨

- 두 정점의 최단 거리 값이 무한대에서 '19'로 바뀜

9. 최단 거리 '12'인 정점이 집합 S에 추가됨

- 한 정점의 최단 거리 값이 '19'에서 '16'으로 바뀜

10. 최단거리 '16'인 정점이 집합 S에 추가됨

11. 마지막 정점이 '19'의 최단거리로 집합 S에 추가되면서 알고리즘이 끝남

다익스트라 알고리즘이 작동하지 않는 예제

ex1. 음의 가중치가 문제를 일으키는 경우

- 간선 하나를 6에서 -15로 바꿈

-> (b)처럼 최단거리 -6으로 바뀌어야 함.

벨만 포드 알고리즘

벨만 포드 알고리즘 개요

- 입력 그래프 G(V, E)에서 간선의 가중치가 음의 값을 허용햐는 임의의 실수인 경우 최단 경로 알고리즘

- 간선을 최대 1개를 사용하는 최단 경로, 간선을 최대 2개 사용하는 최단경로, ... 이러한 식으로 간선을 최대 n - 1개 사용하는 최단 경로까지 구함

벨만 포드 알고리즘 예제

1. 시작 정점 r의 최단거리만 0으로 세팅하고 나머지는 모두 무한대로 초기화

2. 모든 간선을 한번씩 살피면서 해당 간선으로 인해 앞으로 설정한 최단 거리가 더 짧아질 수 있는지 살펴봄

- 시작 정점에 연결된 세 정점만 변동이 생김

- 이들 최단 거리가 무한대에서 8, 9, 11로 각각 바뀜

3. 모든 간선을 다시 한번씩 살피면서 해당 간선으로 인해 앞에서 설정된 최단 거리가 더 짧아질 수 있는지 봄

- 앞에서 세 개의 정점에 변동이 생겼으므로 이번에는 이들로부터 연결된 정점들에 변동이 생길 수 있음

- 이들의 최단거리가 8, 무한대, 무한대, 무한대에서 -6, 10, 19, 19로 각각바뀜

- 이중 -6으로 바뀐 정점은 바로 전단계인 (b)에서도 바뀌었는데 최단 거리 9인 정점으로부터 연결되어 있어 다시 -6으로 바뀜

4. for 루프마다 모든 간선을 한 번씩 살피면서 해당 간선으로 인한 최단거리 변동 여부를 살펴봄

6. 마지막 for 루프 (i=7)에서는 아무런 변동이 일어나지 않음

- 시작 정점에서 7개의 간선을 사용하는 최단경로는 없다는 뜻

최소 신장 트리

1. 최소 신장 트리 개요

2. 프림 알고리즘

3. 크루스칼 알고리즘

최소 신장트리 minimum spanning tree

조건

- 무향 연결 그래프 -> 연결 그래프 : 모든 정점간에 경로가 존재하는 그래프

트리

- 싸이클이 없는 연결 그래프

- n개의 정점을 가진 트리는 항상 n-1개의 간선을 가짐

그래프 G(V, E)의 신장 트리

- 정점 집합 V를 그대로 두고, 간선을 |V| - 1개만 남겨 트리로 구성한것

 -> 아래의 좌측 그림에서 정점 개수는 9개로 사이클을 제거 -> 우측 그림은 9-1 = 8개의 간선을 가진 신장 트리

G의 최소 신장 트리

- G의 신장트리들 중 간선의 합이 최소인 신장 트리

-> 좌측 그래프의 간선을 지우는것에 따라 여러 개의 신장 트리가 만들어 질 수 있음. 

최소 비용 신장 트리를 만드는 알고리즘

1. 프림 알고리즘

2. 크루스칼 알고리즘

프림 알고리즘

- 집합 S를 공집합에서 시작하여 모든 정점을 포함할 떄 까지( 즉, S = V가 될 떄 까지) 키워나감

 -> 맨 처음 정점을 제외하고 정점을 하나 더할 떄 마다 간선이 하나씩 확정 됨

프림 알고리즘 동작 방법

1. 그래프에서 하나의 정점을 선택하여 트리를 만듬

2. 그래프의 모든 간선이 들어있는 집합을 만듬

3. 모든 정점이 트리에 포함되어 있지 않는 동안 트리와 연결된 간선 가운데 트리 속의 두 정점을 연결하지 않는 가장 가중치가 작은 간선을 트리에 추가함

프림 알고리즘 유사 코드

- 프림 알고리즘은 그리디 알고리즘의 일종 -> 그리디 알고리즘으로 최적해를 보장하는 드문 예

Prime (G, r)
{
    S <- 공집합;     // 정점 r을 방문되었다고 표시하고, 집합 S에 포함시킴
    while (S != V){
       S에서 V-S를 연결하는 간선들 중에 최소 길이의 간선 (x, y)을 찾는다. x \in S,  y \in V-S
       정점 y를 방문되었다고 표시하고, 집합 S에 포함시킨다.
    }

}

프림 알고리즘 동작과정

크루스칼 알고리즘

- 싸이클을 만들지 않는 범위에서 최소 비용 간선을 하나씩 더해가면서 최소 신장 트리를 만듦

 -> n개의 정점으로 트리를 만드는데 n-1개의 간선이 필요함

 -> 최소에는 간선이 하나도 없는 상태에서 시작하여 n-1개의 산언을 더하면 더함

 * 프림 알고리즘은 정점을 기준으로 동작한다면, 크루수칼 알고리즘은 간선을 중심으로 동작

크루스칼 알고리즘 작동 예

위상 정렬 개요

- 완수해야할 여러가지 일이 있고 이들 간에 상호 선후 관계가 있는 경우

 -> 유향 그래프의 정점들을 변의 방향을 거스르지 않도록 나열하는 것

ex 1. 특정 수강 과목에 선수 과목이 있는 예

 - 선수 과목 부터 수강해야 함

 - 수강 시 위상 정렬을 통해 올바른 수강 순서를 찾아 낼 수 있음

ex 2. 라면 끓이는 순서 예

위상 정렬의 조건

- 싸이클이 없는 유향 그래프

위상 정렬 topological sorting

1. 모든 정점을 일렬로 나열함

2. 정점 x에서 정점 y로 가는 간선이 있으면 x는 반드시 y보다 앞에 위치해야함

3. 일반적으로 임의의 유향 그래프에 대해 복수의 위상 순서가 존재함

진입 간선

- u에 연결된 간선들 중 u로 향하는 간선

진출 간선

- u에 연결된 간선들 중 u로부터 나가는 가선

위상 정렬의 예시

- 아래의 좌측 그래프에 대한 위상 정렬의 예 2개

위상 정렬 유사 코드

topologicalSort1(G)
{
   for i <- 1 to n {
      진입 간선이 없는 정점 u를 선택함;
      A[i] <- u;
      정점 u와, u의 진출 간선을 모두 제거함;
   }
   이 시점에 배열 A[1 ... n]에는 정점들이 위상 정렬 되어 있음.
}

위상 정렬 알고리즘 작동 예

일상 생활에서 사용하는 많은 부분을 그래프로 나타낼 수 있음

- 지하철에서 역과 역사이의 관계, 사람간의 관계, 네비게이션 길찾기, 한붓 그리기 등

-> 그래프, 그래프 표현방법

그래프

- 현상이나 사물을 정점 vertex와 간선 edge로 표현한 것

- Graph G = (V, E) - V : 정점 집합, E : 간선 집합

- 두 정점이 간선으로 연결되어 있으면 인접하다고 함

 -> 인접 = adjacent

 -> 간선은 두 정점의 관계를 나타냄

그래프 예시

- 사람들간 친분 관계를 나타낸 그래프

- 각 사람을 하나씩의 정점으로 표시

- 서로 친밀한 사람 간에는 간선을 연결함

- 다른 예시

 1. 두 도시를 연결하는 도로의 존재 여부

 2. 두 집안간의 혼인 여부

친분 관계 그래프

- 친밀도를 가중치로 나타냄

- 간선에 가중치를 주어 친밀감의 정도를 보여줌

방향을 고려한 친분관계 그래프

- 간선이 방향을 가짐

- 유향 그래프 : 그래프가 방향을 가진 그래프

 -> 기업들 간 제품 공급 관계

 -> 제품 생산 공정에서 선후 관계 등

- 무향 그래프 : 그래프가 방향이 없는 그래프

가중치를 가진 유향 그래프

- 누가 누구를 얼마만큼 좋아하는지를 나타냄

- 다른 예

 -> 서울과 LA간 비행기 노선 처럼 가는데 걸리는 시간과 오는데 걸리는 시간이 다른 경우

그래프 표현 방법

1. 그래프 표현방법 개요

2. 인접 행렬을 이용한 방법

3. 인접 리스트를 이용한 방법

4. 그래프 탐색

그래프 표현 방법

- 행렬을 이용하는 방법

- 리스트를 이용하는 방법

인접 행렬을 이용하여 그래프를 나타내는 표현

- 인접 행렬(Adjacency Matrix)를 사용

- n x n 행렬로 표현

 -> 원소 (i, j) = 1 : 정점 i와 정점 j사이에 간선이 있음

 -> 원소 (i, j) = 0 : 정점 i와 정점 j사이에 간선이 없음

- 유향 그래프의 경우

 -> 원소 (i, j)는 정점 i로부터 정점 j로 연결되는 간선이 있는지를 나타냄

- 가중치가 있는 그래프의 경우

 -> 원소 (i, j)는 1대신 가중치를 가짐

인접 행렬을 이용한 예

1. 무향 그래프를 인접 행렬로 표현

2. 가중치를 가진 무향 그래프를 인접 행렬로 표현

3. 유향 그래프를 인접 행렬로 표현

4. 가중치를 가진 유향 그래프를 인접 행렬로 표현

1. 무향 그래프와 인접 행렬 표현

2. 가중치를 가진 무향 그래프와 인접 행렬 표현

3. 유향 그래프와 인접 행렬 표현

4. 가중치를 가진 유향 그래프와 인접 행렬 표현

인접 행렬을 이용한 방법의 효율성 분석

1. 이해가 쉽고 간선의 존재 여부를 즉각 알수 있다는 장점을 가짐

 - 정점 I와 정점 j의 인접 여부는 행렬 (i, j) 원소나 (j, i) 원소의 값만 보면 알 수 있기 때문

2. n x n 행렬이 필요하므로 n^2에 비례하는 공간이 필요함

 - 행렬의 준비 과정에서 행렬의 모든 공간을 채우는 데만 n^2에 비례하는 시간이 소모됨

 - O(n^2) 미만의 시간이 소요되는 알고리즘이 필요한 경우에 행렬 표현법을 사용하면 행렬의 준비과정에만 Theta(n^2)의 시간이 소모되어 적합하지 않음

3. 간선의 밀도가 아주 높은 그래프에서는 인접 행렬의 표현이 적합함

 - 전체 (i, j) 쌍에서 둘 중 하나 꼴로 간선이 있는 경우 행렬을 사용하는 것이 효율 적임

 - 100만 개의 정점을 가진 그래프에서 간선이 200만개 밖에 없는 경우에 행렬 표현을 쓰면 시간과 공간이 많이 낭비됨

   -> 행렬의 총 원소 수는 1조개, 이 중 고작 200만(또는 400만) 개만 1로 채워지고 나머지는 0이 되기 때문

인접 리스트 Adjacency List

- n개의 연결 리스트로 표현

- i번째 리스트는 정점 i에 인접한 정점들을 리스트로 연결해 놓은 것 임

- 가중치 있는 그래프의 경우 -> 리스트는 가중치도 보관함

인접 리스트를 이용한 예

1. 무향 그래프와 인접리스트

2. 가중치를 가진 그래프의 인접 리스트

1. 무향 그래프와 인접 리스트₩

2. 가중치를 가진 그래프의 인접 리스트 표현

그래프 탐색

1. 너비 우선 탐색 BFS Breath-First Search

2. 깊이 우선 탐색 DFS Depth-First Search

너비 우선 탐색

- 깊이가 1인 모든 정점을 방분

 -> 깊이가 2인 모든 정점을 방문

 -> 깊이가 3인 모든 정점을 방문 ... (계속 방문)

- 더이상 방문 할 곳이 없으면 탐색을 마침

깊이 우선 탐색

- 깊이 들어가는 특징을 지니고 있음

- 나아갈 길이 존재하지 않으면 이전 위치로 돌아와 다른 길을 선택하여 움직임

행렬 경로 문제

문제 정의

- 양 또는 음의 정수 원소들로 구성도니 n x n 행렬이 주어짐

- 행렬의 왼쪽 위에서 시작하여 한 칸씩 이동해 오른쪽 아래까지 도달

- 방문한 칸에 있는 수들을 더한 값이 이 경로의 합임

이동 방법(제약 조건)

- 오른쪽이나 아래쪽으로만 이동 가능

- 왼쪽, 위쪽, 대각선 이동은 허용하지 않음

목표

- 행렬의 왼쪽 위에서 오른쪽 아래까지 이동하되, 방문한 칸에 있는 수들을 더한 값이 최대화 되도록 함

불법 이동의 예

- 위쪽이나 왼쪽으로 이동하여선 안됨

유효한 이동의 예시

최적 부분 구조

- c_ij를 원소 (i, j)에 이르는 최고 점수라고 정의.

- m_ij는 행렬 원소 (i, j)의 값

1. i = j = 1이면 원소 (1, 1)에 이르는 최고 점수를 구하는 것.

 -> 원소 (1,1)만 방문하므로 원소 (1, 1)의 값이 답

2. i = 1, j > 1이면 첫째 행의 한 원소에 이르는 최고 점수를 구하는 것

 -> 첫째 행을 따라 오른쪽으로 수평 이동하는 방법밖에 없음. 따라서, (1, j)의 바로 왼쪽 원소 (1, j-1)에 이르는

   점수 ((1, j - 1)에 이르는 유일한 점수이자 최고 점수)에 원소 (1, j)의 값을 더하면 됨.

3. i > 1, j = 1이면 첫째 열의 한 원소에 이르는 최대 점수를 구하는 것

 -> 첫째 열을 따라 수직 이동하는 방법 밖에 없음. 따라서 (i, 1)의 바로 위쪽 원소 (i-1, 1)에 이르는

   점수 ((i-1, 1)에 이르는 유일한 점수이자 최대 점수)에 원소 (i, 1)의 값을 더하면 됨

4. '1, 2, 3'의 경우가 아니면

 -> 원소 (i, j)의 바로 왼쪽 원소에 이르는 최고점수와 원소 (i, j)의 바로 위쪽 원소에 이르는 최고 점수 중 큰 것에

   원소 (i, j)의 값을 더한 것이 원소 (i, j)에 이르는 최고 점수 임.

재귀적인 알고리즘의 유사 코드

matrixPath(i, j) (i, j)에 이르는 최고 점수
{
   if (i = 1 and j = 1) then return m_11;
   else if (i=1) then return (matrixPath(1, j-1) + m_1j);
   else if (j=1) then return (matrixPath(i-1, 1) + m_i1 ;
   else return ((max(matrixPath(i-1, j), matrixPath(i, j-1)) + m_ij);
}

호출 트리

mathPath()에서 문제 크기가 커짐에 따라 중복 호출이 증가

=> 부분 문제들의 총 수는 n^2, 중복 호출 회수는 지수적으로 증가

동적 프로그래밍을 이용한 유사 코드

mathPath(n) //(n, n)에 이르는 최고 점수
{
   c[1, 1] <- m_11;
   for i<-2 to n
      c[i,1] <- m_i1 + c[i-1, 1];
   for j<-2 to n
      c[1,j] <- m_1j + c[1, j-1];
   for i<-2 to n
      for j<-2 to n
         c[i, j] <- m_1j + max(c[i-1, j], c[i, j-1]);
   return c[n, n];
}

-> Theta(n^2)의 시간 복잡도

재귀적 해법

- 큰 문제에 닮은 꼴의 작은 문제가 깃듬

- 잘쓰면 보약, 못쓰면 맹독

 -> 관계 중심적으로 파악함으로써 문제를 간명하게 볼 수 있음

 -> 재귀적 해법을 사용하면 심한 중복 호출이 일어나는 경우가 있음

재귀적 해법이 바람직한 경우

- 퀵/병합 정렬 등 정렬 알고리즘

- 계승 구하기

- 그래프의 dfs 깊이 우선 검색

재귀적 해법이 치명적인 경우

- 피보나치 수 구하기

- 행렬 곱샘 최적 순서 구하기

동적 프로그램이의 기원

- 미국의 수학자 리처드 벨만이 1940년대 사용하던 용어

- 큰 문제안에 작은 문제가 중첩되어 있는 문제를 해결하는데 사용하는 방법을 동적 계획법이라 이름 붙임

- dynamic 이란 말은 벨만이 이런 알고리즘의 시가변적이며 다단계적인 특성을 나타내기 위해 채택한 용어

- programming 이란 단어는 공군 내에서도 워드프로세스 교육이나 군수 물자 운송 등에 이용되는 단어였기 때문에 사용하는데 아무 제약이 없었던 것임

동적 프로그래밍이란

- 큰 문제의 해답에 작은 문제의 해답이 포함되어 있고, 이를 재귀 호출 알고리즘으로 구현하면 지나친 중복이 발생하는 경우에 재귀적 중복을 해결하는 방법

- 재귀적 중복을 해결하기 위해, 적절한 저장 방법으로 중복 호추르이 비효율성을 제거 한 것

동적 프로그래밍 조건

- 최적 부분 구조를 이루어야함

- 재귀적으로 구현했을때 중복 호출로 심각한 비효율이 발생함

동적 프로그래밍 전략

- 기본적으로 분할 정복 알고리즘과 비슷

- 동적 프로그래밍을 사용하는 알고리즘 역시 주어진 문제를 부분 문제로 나누어 각 부분문제의 답을 계산하고, 이 계산한 결과 값을 이용해 원래 문제의 답을 산출하기 때문

분할 정복 알고리즘과의 차이점

- 분할 정복 알고리즘 : 원래 문제를 부분 문제로 나눔

- 동적 프로그래밍 : 주어진 부분 문제 정담답을 저장 해둔 뒤 동일 문제를 이용 할 때 저장해둔 정답을 바로 산출하여 이용함(속도 향상)

피보나치 수의 정의

- f(n) = f(n-1) + f(n-2)

- f(1) = f(2) = 1

- n의 피보나치 수는 n-1의 피보나치 수와 n-2의 수를 포함함

-> 최적 부분 구조 : 이처럼 큰 문제의 해답에 작은 문제의 해답이 포함 된 경우

피보나치 수를 구하는 재귀 알고리즘

fib(n)
{
  if (n = 1 or n = 2)
     then return 1;
     else return (fib(n - 1) + fib(n - 2));
}

-> 중복 호출이 많이 발생

피보나치 수열의 재귀 알고리즘 call tree

- fib(3)을 구할떄는 fib(2)와 fib(1)이 필요

- fib(4)을 구할때 fib(2)가 2번 호출

- fib(5)는 fib(2)가 3번 호출

- fib(6)을 구할때는 fib(2)가 6번 호출

중복 호출이 증가하는 정도

- 중복 호출 회수 자체가 다시 피보나치 수열을 이름

- 증가 속도 : Omega(2^{n/2}) -> 지수 함수적

동적 프로그래밍을 이용한 해법

- 접근 방법 : 중복되는 호출 결과를 한번만 구해 저장해 놓았다가 나중에 다시 사용

- ex : fib(3)을 처음 호출하고 결과를 얻었으면 이것을 어딘가에 저장해두고 나중에 fib(3)이 필요하면 저장된 것을 이용

피보나치 수열과 동적 프로그래밍 조건

- 최적 부분 구조를 이루어야 함 -> 만족

- 재귀적으로 구현했을때 중복 호출로 심각한 비효율이 발생함 -> 만족

=> 동적 프로그래밍이 그 해결책

피보나치 수를 구하는 동적 프로그래밍 해법 유사 코드

fibonacci(n)
{
   f(1) <- f(2) <- 1;
   for i <- 3 to n
      f[i] <- f[i-1] + f[i-2];
   return f[n];
}

=> Theta(n) 시간에 끝난다.

해시

- 원재료를 다른 재료와 함께 다지고 섞어서 새로운 형태의 요리로 만드는 것

자료구조의 해시

- 데이터를 입력 받으면 완전히 다른 모습의 데이터

해시 테이블 개개요

- 아래의 배열에서 623453을 찾기 위해서 어떻게 해야할까?

- 지금 상태에서는 순차 탐색 밖에 대안이 없음

-> 원하는 값이 k번째에 있는 경우 k번 비교 연산을 수행해야함

해시 테이블 개요

1. 원소가 저장될 자리가 원소의 값에 의해 결정되는 자료 구조

- 저장된 자료와 비교를 통해 자리를 찾지 않고 단 한번의 계산으로 자신의 자리를 찾음

2. 직접 주소 테이블 direct address tables

- 원본 데이터의 키를 직접 주소 테이블의 주소에 바로 기재하는 방법

  -> 크기가 |U|인 테이블 T를 생성하고 키 k를 slot k에 저장하는 방식

- 키가 중복되어서는 안됨

3. 평균 상수 시간에 삽입, 삭제, 검색

- 매우 빠른 응답을 요구하는 응용에 유용함

 -> ex : 119 긴급구조 호출과 호출번호 관련 정보 검색, 주민등록시스템

- 해시 테이블은 최소 원소를 찾는 것과 같은 작업은 지원하지 않음

해시 테이블의 예시

- 입력 : 25, 13, 16, 15, 7

- 해시 함수 h(x) = x mod 13

-> 탐색 성능은 향상되었으나 저장 공간은 희생 됨

해시 함수

- 키 값을 입력으로 받아 해시 테이블 상 주소를 리턴

- 해시 함수가 가져야 하는 성질 : 입력 원소가 해시 테이블 전체에 고루 저장되어야 함. 계산이 간단해야함

해시 함수 종류

1. 제산법 division method

2. 곱하기 방법 multiplication method

3. 제곱법 mid square

4. 숫자 분석법 digit analysis

5. 이동법 shifting

6. 기수변환법 radix conversion

7. 접지법 floding

8. 난수 생성법 pseudo random

9. 대수적 코딩 algebraic coding

10. 자릿수 재배열