집밖은 위험해

컴퓨터 비전에서의 기계학습

- 주어진 영상에 대해 특징 벡터 추출 -> 분류기 학습 (학습 집합 생성) -> 입력 영상 분류

- 분류기(학습 모델) 종류 : 신경망, SVM, 에이다부스트, 랜덤포래스트

특징 벡터 수집 방법

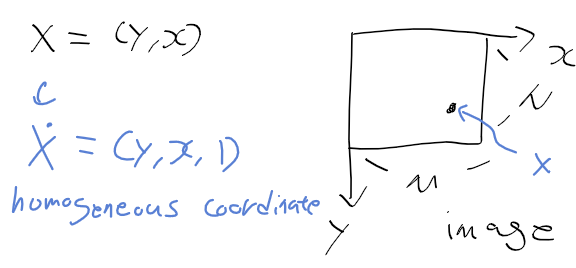
1. 일정 영역

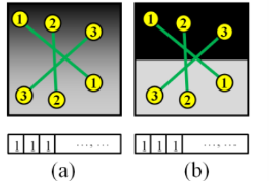
2. 슬라이딩 윈도우

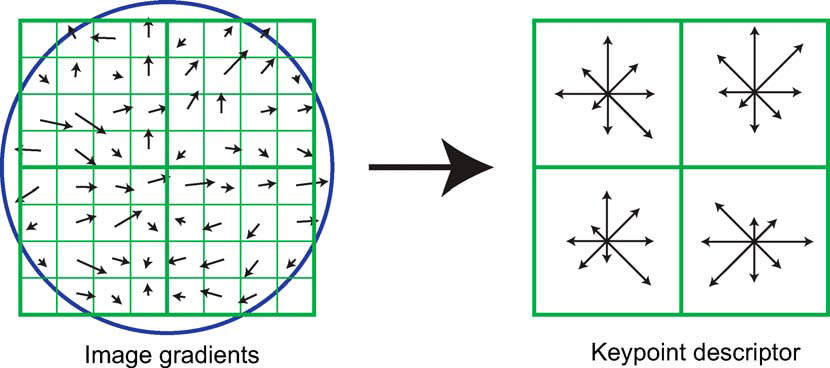
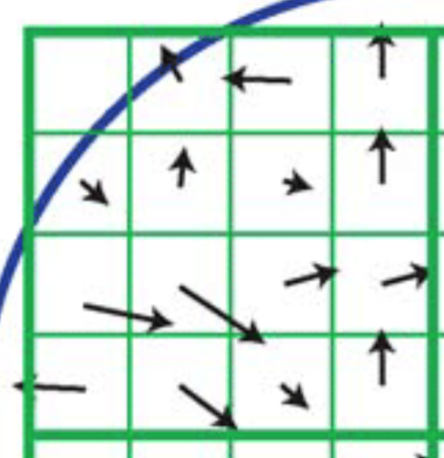
3. 특징점

신경망

- 퍼셉트론 가중치들을 나타내는 매개변수 집합이 존재

- 목적 함수 : 매개 변수들의 값이 적절한지 판단

- 학습 집합 : 최적의 매개변수를 추정하도록 사용하는 데이터 

  => 매개변수가 일정 조건에 수렴할떄까지 반복

- 검증 집합 : 학습된 신경망을 검증하기 위한 데이터 집합

- 모델 선택 : 신경망 모델이 만족스럽지 못한 경우 개선된 모델 선택

- 과적합 overfitting : 신경망 학습시 아웃라이어들에도도 과하게 최적화된 상태. 일반적인 경우 잘못 분류할수 있음

성능 개선 및 평가 기법들

- 리샘플링 : 같은 샘플을 여러번 사용

- k겹 교차 검증 : 전체 샘플을 k 등분 하여, 각각의 부분집합 k-1개로 학습, 나머지 1개 부분집합으로 검증

- 부트스트랩 : 검증시 샘플의 중복을 허용함

kd트리 매칭

- 지역 정보만 사용

 => 첫 영상의 특징 벡터와 둘째 영상의 특징 벡터에서 최근접 이웃을 탐색하여 대응쌍 구함

기하 변환 Geometry Transform의 예시

- 같은 물체인 다른 대응쌍이 존재시. 기하 변환은 비슷해야함

- 예시 : Rigid Transform, Affine Transform, Perspective Transform 등

kd트리 매칭과 기하 변환

- kd트리 최근접 이웃 탐색을 이용한 매칭에서는 기하 정렬 조건 고려 x, 지역 정보만 사용

=> 기하 정렬 필요

기하 정렬 알고리즘의 사용 예시

- 잡음, 가림, 섞임에도 강건한 알고리즘으로 다음들이 존재

 -> 최소제곱법(거짓 긍정이 없는 상황), RANSAC(거짓 긍정이 존재하는 경우). 상황에 맞게 적절히 사용함

- 아래의 그림은 다양한 특징에다가 기하 정렬 알고리즘을 통해 매칭한 예시들을 보여줌

최소제곱법 least square method

- 주어진 샘플들을 가장 잘 표현하는 모델을 구함

- 아래의 예시는 점 집합이 주어질때 오차가 가장 적은 직선을 구하는 그림

컴퓨터 비전에서의 최소제곱법

- 일반 최소 제곱법에서 점 집합이 주어졌으나, 컴퓨터 비전에서는 특징 집합 X가 주어짐

- 대응 쌍이 같은 물체에 존재한다면, 같은 기하 변환을 가짐.

- 기하 변환 행렬(동차 변환 행렬) : 회전, 평행이동, 크기 변환 등을 포함

- 특징의 변환 : 아래의 동차 좌표가 주어질때, 동차 좌표와 동차 변환 행렬의 곱으로 기하 변환 결과 좌표를 구함. 

- 실제 측정한 점 b와 기하 변환을 통해 얻은 점 b' = x_dot H_dot이 주어질때,

  b와 b'의 최소 제곱 오차가 가장 줄여주는 기하 변환 행렬을 구해야 함.

최소제곱법을 이용한 매칭 예시

- 두 영상과 특징들이 주어질때, 매치 오차를 최소화 하는 기하 변환 행렬을 구한 예시

RANSAC을 이용한 매칭

- 두 영상의 특징 매칭 쌍 중에 거짓 긍정이 포함된 경우. 이를 노이즈로 보고 노이즈를 제거해야함

 => RANSAC 사용

순수 매칭 알고리즘

- 첫 영상 특징 벡터들에 대한 둘째 영상의 최근접 이웃 구함

=> 매칭쌍들을 mlist에 모음

- 아래의 그림은 이진 검색

kd트리

- 이진 검색트리의 예시

- 왼쪽 자식 노드는 기준 노드보다 작고 오른쪽 자식 노드는 기준 노드보다 큼

- 검색 키 : kd 트리에서 찾아야될 노드의 값

kd 트리 생성

- 특징

 1. 검색키는 스칼라가 아니라 벡터

 2. 검색 키에 가장 가까운 최근접 이웃 노드를 찾아야 함 

- n개의 특징벡터 X로 kd 트리를 만드는 경우, 하나의 특징 벡터 x는 d차원 벡터

- 루드 노드가 X를 두 부분 집합 X_left와 X_right로 분할

 -> 자식 노드에서도 계속 분할을 수행 => kd 노드 생성

kd 트리에서의 최근접 이웃 탐색

- 목표 : 특징 벡터 x입력이 주어질때 최근접 이웃을 찾기

- 입력 : x = (20,20)

- 과정 : 루트노드에서부터 분할해 나가며 입력에 가까운 노드를 찾아나감 -> 입력 벡터 x는 노드C에 최근접이웃

매칭 성능 판단

- 스테레오 비전과 파노라마서 여러장의 영상으로 매칭 수행

- 두 영상으로 매칭하는 경우. 첫 영상의 특징 벡터 a와 두 영상의 특징 벡터 b가 잘 매칭 => 매칭 쌍으로 판단

- 두 특징 벡터 a, b의 거리가 임계치 T보다 작으면 매칭쌍

임계치 설정하기

- T가 매우 작으면, 아주 가까운 쌍만 매칭

 => 진짜도 실패할 수 있음. 거짓 부정 FN 많이 발생

- T가 크면

 => 아닌 것도 성공함. 거짓 긍정 FP 발생

ROC Receiver Operating Charateristic 곡선

- 거짓 긍정률 FPR과 참 긍정률 TPR을 이어 만든 곡선

 => 매개변수에 따라 TP와 FP의 변화를 쉽게 보여줌

매칭 전략

- 서로 다른 영상에서 존재하는 특징이 매칭쌍인지 판단하는 방법

1. 고정 임계값 방식 : 거리가 고정된 임계값보다 작은지 확인 

2. 최근접 이웃 : 첫 영상의 특징 벡터 a가 주어질때 둘째 영상에서 최근접 벡터 b를 찾음.

3. 최근접 거리 비율 : 첫 영상 특징 벡터 a가 주어질때, 둘째 영상에서 최근접 특징벡터 b1과 다음으로 가까운 b2 취득

                      -> d(a, b1)/ d(a, b2) < T 이면 매칭

=> 최근접 거리 비율이 가장 좋은 성능을 보임

컴퓨터 비전에서의 매칭

- 서로 다른 영상간의 특징점 쌍이 동일한 것인지 확인하는 과정

- 유사성 or 거리를 측정하여 확인

 => 특징점 쌍 매칭에 거리 + 유사도 측정 척도가 필요

매칭에 사용하는 특징

- 에지

- 지역 특징

- 영역

SIFT 기술자의 거리재기

- SIFT 기술자는 128차원

- 두 점 a, b가 주어질때 이들의 거리를 측정해야함

- 방법 : 유클리디안 거리, 마할라 노비스 거리

유클리디안 거리

- 두 점 a, b가 주어질때, a와 b의 차로 구한 내적

- 유클리디안 거리가 작다 => 같은 지점을 나타낸다.

마할라노비스 거리

- 분산을 고려한 거리

- 아래의 경우 평균 mu와 점 b, 점 c가 주어질때 유클리드 거리상 점 b가 가까우나 이는 노이즈

- 점 c가 점 b보다 mu에 가깝다고 봐야함

=> 마할라노비스 거리 : 공분산을 고려한 거리

얼굴 인식

- 컴퓨터 비전 분야에서 주성분 분석을 가장 잘 사용하는 경우로 얼굴 인식이 있음.

평균 얼굴

- 여러개의 얼굴에 대한 평균 영상

고유 얼굴

- 얼굴 영상에 PCA를 적용하여 얻은 고유 벡터

1) 평균 얼굴 획득

2) 입력 얼굴 영상 - 평균 얼굴

3) 공분산 행렬 취득

=> 고유 벡터와 고유값 계산

고유 얼굴 이용한 얼굴 인식

1. 원래 얼굴 벡터 x로 고유 얼굴 벡터 y 획득

2. 입력 얼굴 xi가 주어지면 고유 얼굴 yi로 변환

3. 입력 고유 얼굴 yi와 고유 얼굴 벡터 y의 원소 들 중 거리가 가장 가까운것을 검색

* 거리가 임계값이상이면 다른사람, 없는사람

주성분 분석 PCA Principal Component Analysis

- 고차원의 벡터를 정보의 손실을 줄여 저차원의 벡터로 변환하는 기술

 => 차원 축소, 변수 추출 방법으로 널리 사용됨

- 아래의 예시에서 2차원 데이터를 1차원 데이터로 변환한 예시들을 보여줌

 => 원래 데이터의 분산을 가장 잘 보존하는 축을 찾아야 함

텍스처

- 특징 추출, 영역 분할에서 많이 사용

- 영상의 질감 -> 반복되는 일정 패턴

텍스처 분석과 구조적 방법

- 구조적 방법 structural method

-> 기본 요소텍셀을 추출후 텍셀의 공간적 배열 탐색

- ex. 꽃밭 영상의 경우 -> 꽃이 텍셀

- 텍스처를 추출 할 대상은 지역적일수도 전역적일수도 있음 -> 어렵게 만듬

전역 기술자

1. 영상의 에지를 텍스처 기술자로 사용

2. 명암 히스토그램을  사용

=> 문제: 지역적 변화는 반영 불가

지역 관계 기술자

- 픽셀 간 관계 정의 및 표현 방법 필요

-> 동시 발생 행렬, 지역 이진 패턴

동시 발생 행렬 coocurrence matrix

- 명암 픽셀 쌍들을 조사하여 이웃간의 관계 정의 필요.

- 동시 발생행렬에서 행은 픽셀 쌍의 명암값, 열은 발생 횟수 표현

-> 명암 영상은 길이가 256이므로 256 x 256 크기로 동시 발생 행렬이 만들어짐.

지역이진패턴

- 지역적인 영역의 이진 패턴으로 텍스처 기술

- 종류

LBP Local Binary Pattern

LTP Local Ternary Pattern

LBP 지역 이진 패턴

- 텍스처 분류를 위한 특징이나 얼굴 인식 등에서도 많이 활용

- 모든 픽셀에 대해 계산. 중심 픽셀 주위의 밝기 변화를 이진화한 패턴

LBP와 얼굴인식 예시

- 얼굴 영역을 일정 크기 셀로 분할

- 각 셀별 LBP 히스토그램(LBP 인덱스 값에 대한) 계산

- 히스토그램들을 직렬로 연결한 벡터를 최종 특징으로 사용

 => 일종의 탬플릿 매칭

 * 셀 단위로 기하학적 정보 유지, 셀 내에선 텍스처 정보만 추출

LBP의 단점

- 명암이 균일한 부근에서 불안정

-> 명암들이 비슷한 부분에서는 어떻게 0과 1로 이진화 시킬까?

LTP Local Ternary Pattern

- 매개변수 t를 설정

- 중간 픽셀 화소에서 +- t 범위 안이면 0. +t보다 크면 1, -t보다 작으면 -1

- LTP 생성 : 2개의 LBP 생성됨 -> 512차원

=> 0, -1 -> 0, 1 -> 1으로 히스토그램 생성. LBP 1개

=> 1, 0 -> 0, -1 -> 1으로 히스토그램 생성. LBP 1개

PCA-SIFT

- 주요 방향 dorminant direction을 구하는 과정은 SIFT와 동일

- 특징 벡터 x 추출 과정이 다름

1) 키포인트 중심으로 39 x 39 윈도우 씌움

2) 윈도우 안 픽셀에 대해 y방향 x방향 도함수 영상 계산

3) 39 x 39 = 3,042 차원 벡터 획득 -> 너무크다

4) PCA Principal Component Analysis 주성분 분석으로 차원 축소하여 특징벡터 x로 취급

=> 4 * 4 * 8 = 128차원인 SIFT 기술자보다 PCA-SIFT는 차원 수를 크게 줄일수 있음

GLOH

- Gradient Location Orientation Histogram

- 원형 마스크(필터, 윈도우) 사용

- 원은 3등분, 두 바깥원들은 각각 8등분

- 분할된 영역들(16 + 1= 17개)에서 16단계 그라디언트 방향 히스토그램 계산

=> 17 x 16 = 272 차원 특징 벡터

- PCA 수행하여 272 -> 128차원 특징벡터로 취급 

이진 기술자

- 이전에 살펴본 특징 기술자들은 개당 128차원의 특징 벡터로 영상 처리하기엔 너무 큼

- 특징점 주위 두 픽셀을 비교쌍으로 사용. 픽셀들을 조사 후 수백개의 쌍으로 이진 배열 생성

- ex: BRIEF, ORB, BRISK

- 이진 기술자 조서 패턴 : 특징점 주위의 비교쌍들의 한쪽은 1, 한쪽은 0의 값을 가짐

이진 기술자들의 특징

- BRIEF : 가우시안을 따르는 두 점 조사 -> 스케일/회전에 영향 받음. 256개의 비교쌍 -> 256비트

- ORB : 회전 불변, 512 비트

- BRISK : 60개 점 설정 및 거리 조건 만족하는 쌍만을 비교쌍으로 사용. 회전 + 스케일 불변, 512 비트

이진 기술자와 일반 기술자 비교

- BRISK : 512비트

- SIFT 기술자 : 특징점 주위를 4등분. 한 영역에 4 x 4 x 8 = 128바이트. 128 x 4 = 512바이트

- BRISK의 크기 = SIFT 기술자의 크기/8

기술자 descriptor

- 특징점 내부와 주위로 부터 얻은 정보와 정보 추출 알고리즘

 => 특징에 대해 설명해줌

- 특징 벡터 feature vector : 일정 크기의 벡터임

특징 벡터와 기술자

- 패턴 인식에서 특징 벡터, 영상 처리에서 특징의 정보를 기술자라고 주로 부름

- SIFT, SURF와 같이 개선된 특징점 검출 알고리즘을 구했다면, 기술자도 좋은 기술자를 구해야함.

특징 기술자 성질

- 기술자끼리 구분 가능해야함 -> 이후 매칭시 대응하기 위함

- 불변성 : 영상이 회전, 크기, 광도 등 변환이 일어나도 기술자는 불변해야함

- 특징 벡터의 크기를 줄여야 함 -> 한 영상에서 특징 수천개 존재, 매칭시 특징간 거리 계산하므로 차원이 낮아야함.

관심점의 정보

- 스케일 정보가 없는 경우 (y, x)

- 스케일 정보를 갖는 경우 (y, x, omega)

SIFT 특징

- 키포인트라고도 부름

- 스케일 정보를 가진 (y, x, omega) 형태 -> 스케일 변환에 불변

- 회전 변환에 불변하기 위한 정보가 필요

주요 방향의 필요성

- 회전 불변하기 위한 정보가 필요 -> 주요 방향 dominant orientation을 우선 찾음

 1) 키포인트 중심으로 윈도우(커널)

 2) 윈도우 내 픽셀에 대해 그라디언트 방향 히스토그램으로 주요 방향 찾음

  * 10도 간격으로 양자화 -> 히스토그램은 36칸 가짐

  * 그라디언트 크기에 가우시안을 컨볼루션하여 멀수록 작은 가중치 반영

  => 히스토그램에서 가장 큰 값을 나타내는 방향이 주요 방향

- 아래의 그림은 이미지 그라디언트와 키포인트 기술자 예시

 * 좌측은 방향이 10도 간격으로 양자화(36단계)됨, 우측은 8단계로 양자화된 그라디언트 방향 히스토그램

키포인트 정보

- (y, x, omega, theta)로 정리.

- 기술자를 얻기 위해 윈도우 컨볼루션

 * 주요 방향이 기준이 되도록 좌표계 설정 -> 방향 불변성 성립

1) 위 그림에서 한박스만 보자. 윈도우를 4x4로 분할하여 블록이 16개 존재. 현재 10도 간격으로 36단계의 방향이 표현됨

2) 위 블록에 존재하는 16픽셀의 그라디언트를 계산하여, 8단계 양자화된 그라디언트 방향 히스토그램 추출

=> 이 데이터는 4(가로박스 개수)x4(새로박스 개수)x8(방향) = 128차원의 특징 벡터 x가 됨

3) 벡터 x를 벡터의 크기 ||x||로 나누어 단위 벡터 획득

 => 회전, 광도 불변한 128차원 SIFT 특징 기술자 완성

SIFT 기술자 추출기

- 입력 : SIFT detector로 검출한 특징점(관심점, 키포인트 - y, x, omega)

- 출력 : 키포인트(기존의 키포인트 + 주요 방향 + 특징벡터 x)