집밖은 위험해

(생략했지만)

 이전까지는 해리스 같은 코너 검출기들을 살펴보았습니다. 이들은 회전 불변으로, 이미지가 회전이 된다해도 같은 코너점을 찾을수가 있겠습니다. 하지만 크기변화에선 어떨까요?

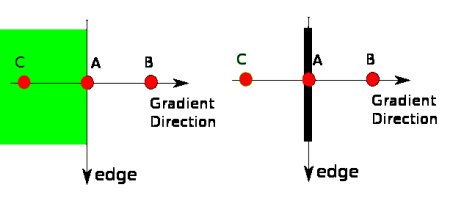
 이미지가 크기가 조정되면 코너가 더이상 코너가 안될수도 있습니다. 예를들자면 아래의 그림을 한번 살펴보세요. 왼쪽 그림에서 코너는 작은 윈도우에 들어갔지만, 줌해서 커진경우에는 여러 부분들을 찾을수가 있겠습니다.

 그래서 해리스 코너는 크기 변화에 불변하지 않다고 얘기 합니다.

 2004년 D.Lowe는 새로운 알고리즘으로 크기에 불변한 특징 변환 이라고 하는 SIFT 알고리즘을 제안하였습니다. 여기서 크기 불변 키포인트로 이미지 특징이라는 논문에서 키포인트를 추출하고, 기술자를 계산하는 방법에 대해서 소개하고 있습니다. 

 SIFT 알고리즘에대해서 4단계로 나누어 설명해보겠습니다.

1. 크기 공간 극점 검출 Scale-space Etrema Detection

 위 그림을 보시면 다른 스케일의 키포인트를 검출할때 같은 크기의 윈도우를 사용할수가 없는걸 봤었습니다. 작은 코너라면 괜찬겠죠. 하지만ㄴ 큰 코너를 구한다면 큰 윈도우가 필요할겁니다.

 이것떄문에 크기 공간 필터가 사용됩니다. 이를 위해서 다양한 분산 값 omega을 가진 이미지의 LoG Laplacian of Gaussian을 구해보겠습니다. LoG는 방울 검출기 처럼 동작을할건데 omega의 값 변화에 따라 다양한 크기의 blob을 검출하게 될겁니다.

 여기서 omega는 스케일 파라미터로 사용되어, 위 영상에서 omega가 작은 가우시안 커널을 사용한다면 작은 코너들을 찾아낼것이고, 큰 omega값을 가진 가우시안 커널을 사용시 큰 코너들을 찾아낼 겁니다.

 이렇게 해서 다양한 스케일에 대해 지역 극대점을 찾아내고, 이들을 (x, y, omega)값의 목록으로 정리하겠습니다. 이 값의 의미는 omega 스케일의 공간에서 (x, y)에서 키포인트를 의미합니다.

 하지만 LoG는 계산하기에는 비용이커 SIFT 알고리즘은 DoG Differeence of Gaussian을 사용하게되는데 이는 LoG를 근사시킨거라고 할수 있겠습니다. DoG 필터는 두개의 다른 omega로 블러링한 가우시안 영상의 차이로 얻을수가 있겠습니다. 이 방법은 가우시안 피라미드에서 다른 옥타브를 가진것끼리 차 연산을해서 얻을수가 있겠습니다.

 그래서 DoG를 구하면, 크기와 공간에 대해서 지역 특징들을 찾을겁니다. 어느 이미지에서 한 픽셀들은 주위의 8개 이웃과 비교할거고, 또 이전 스캐일의 9픽셀과 비교하겠습니다. 이 픽셀이 지역적으로 극점이라면, (잠재적인 키포인트라 판단하고) 해당 스케일에서 최적인 키포인트가 되겠습니다.  이에 대한 그림은 아래와 같습니다.

 이 논문에서는 4개의 옥타브와 5개의 스케일 레벨이 주어지고, 초기값으로 omega = 1.6, k = root(2)를 줄때 최적의 결과를 얻을수 있다고 합니다.

2. 키포인트 위치 추정 keypoint localization

 잠재적 키포인트의 위치를 찾아내었다면, 실제 결과를 얻기 위해 재정의 하겠습니다. 극점의 정확한 위치를 얻기 위해 스케일 공간에 대해 테일러 전개를 사용할건데, 이 극점에서의 강도가 임계값 0.03(논문에서)보다 작다면 극점이 아닌것으로 판단합니다. 여기서 사용하는 임계치를 contrastTrheshold라 부릅니다.

 DoG는 에지에서 강한 응답을 보이는데, 그래서 에지를 제거하여야 합니다. 해리스 코너에서 본것과 비슷한 컨샙을 사용할건데, 2 x 2 해시안 행렬을 사용해서 곡률을 계산하겠습니다

 . 해리스 코너 검출기에서 에지의 경우 고유값은 다른것보다 크다는 사실을 알고 있으므로, 이를 간단한 함수로 사용할수 있는데, 이 비율이 임계치보다 크면 그 잠재적 키포인트는 제거하겠습니다. 이렇게 하여 차이가 적은 키포인트와 에지들을 제거하여 강인한 점들만 남게 됩니다.

3. 방향 할당 orientation assingment

 각각의 키포인트에는 이미지 회전에 강인할수 있도록 방향이 배정됩니다. 키포인트 주위에 있는 이웃점들은 스케일에 의존하고, 그라디언트 크기와 방향은 이 공간에서 계산할수 있겠습니다. 360도 방향을 다루기위해 36개의 이진 값을 가진 방향 히스토그램을 만들겠습니다.

 이 히스토그램은 가우시안 크기와 가우시안 가중치 원형 윈도우(oemga는 1.5인)으로 가중화 될건데, 히스토그램의 가장 높은 지점이나 80%이상인 지점을 방향으로 계산하겠습니다. 이를 통해 같은 크기위 위치를 가졌으나 다른 방향인 키포인트가 만들어지겠습니다. 이 개념이 추후 매치하는데 사용되겠습니다.

4. 키포인트 기술자 keypoint descriptor

 이제 키포인트 기술자를 만들어보겠습니다. 키포인트 주위에 16 x 16크기의 이웃점들을 사용할건데 이들을 4 x4 크기의 16개 작은 블록으로 나누겠습니다. 각각의 작은 블록들을 8 이진 방향 히스토그램으로 만들겠습니다. 총 128개의 이진 값들을 얻겠습니다. 이렇게 얻은 벡터를 기포인트 기술자라고 부르겠습니다. 키포인트 기술자를 사용해서 조명 변화나 회전에 강인해질수 있겠습니다.

5. 키포인트 매칭

 두 영상 사이의 키포인트를 주위의 최근접 이웃들을 확인해서 매치시킬수가 있겠습니다. 하지만 어떤 경우에는 가장 가까운것보다 두번째것들이 가장 가까울수가 있는데요. 이 경우에는 노이즈나 다른 이유로 발생할수도 있겠습니다. 이 경우에는 두번째 최근접 거리에 대한 최근접 거리의 비율이 필요하겠습니다. 0.8보다 크면 이들은 제거되어 90% 오탐을 제거하는 반면에 5%의 정탐만을 제거한다고 합니다.

import cv2
import numpy as np

img = cv2.imread('./res/home.jpg')
gray= cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

sift = cv2.SIFT_create()
kp = sift.detect(gray,None)

#img=cv2.drawKeypoints(gray,kp, img)
img=cv.drawKeypoints(gray,kp,img,flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)

cv2.imshow("img",img)
cv2.waitKey(0)
cv2.destroyAllWindows()

- 위 코드에서 kp는 키포인트들의 목록이고, des는 키포인트의 배열로

(kepyoint 개수) x128 형태가 된다고 한다.

sift.detect()에서 죽으니 대신 결과 캡처해서 올린다.

=> 보니까 기존의 opencv-python 튜토리얼은 이전 버전 기준이라 죽었었다.

opencv 4.4.0 기준 현재 수정한 코드를 사용하면 잘 동작된다.

이번 장의 목표는 피처에 대해서 이해하고 이게 왜 중요한지, 코너가 왜 중요한지 배워나가겠습니다.

 많은 분들이 퍼즐을 해보신적이 있을겁니다.  이미지의 여러 조각들이 주어지고 이것들을 모아 큰 임지ㅣ를 만들어야 합니다. 어떻게 이런것들을 할수 있을까요? 이와 같은 논리를 컴퓨터 프로그램으로 할수 있지 않을까요? 

 이걸 해내기 위해서 고유하고, 쉽게 추적할수 있고, 비교하기 좋은 특정한 패턴/특징들을 찾고자 합니다. 특징은 이미지의 모든 방향으로 변화가 큰 부분을 말하며, 이런 특징들을 찾는것을 특징 검출이라 합니다.  특징들을 찾았다면 다른 영상에서 같은 부분을 찾고싶을 겁니다. 이건 어떻게 할까요?

 이 그림에서 한번봅시다. 윗 부분은 파란 하늘이고 아래는 건물들로 되어있는데 여기서, 특징들이 이 이미지의 어디에 있는지 찾아봅시다. 여러분들은 특징에 대해 조사해보고 컴퓨터도 특징에 대해서 살펴볼겁니다. 이에 대한 설명(기술)을 특징 기술자라고 부릅니다.

 특징과 기술자를 찾는다면 모든 이미지에서 찾을수 있고, 나열하며 이을수도 있겠습니다. 앞으로 살펴볼 것들은 어떻게 opencv에서 특징들을 찾고, 기술하고, 매치시키는지 배워보겠습니다.

그동안 수학적 이론을 공부하면서 컴퓨터 비전 전반에 대해 간략하게 살펴봤었다.

하지만 컴퓨터 비전으로 뭘 할수있는지는 알겠으나 이걸 어떻게 할수있는지 잘 모르겠더라

그래서 수학적 알고리즘을 하나하나 구현해봐야 되는건가 싶어

잠시 파이썬으로 히스토그램 평활화를 구현해보기도 했으나

이런 방식으로 해선 끝도 없겠더라

그래서 다른 방향은 opencv에 있는 예제들을 대부분 한번 해보면 다음에 무엇을 할지 정리되지 않을까 싶은 마음에 시작했다.

컴퓨터 비전 분야에서 내가 하고싶은 목표는 특징을 이용한 그래프 기반 슬램을 구현하는것으로

물론 내가 밑바닥 부터 구현할수는 없으니 적어도

특징 검출, 비주얼 오도메트리, 비주얼 슬램 순으로 해보곤 싶었다.

그에 앞서 opencv로 어떤것들을 할수 있는가 고민하다가

opencv 예제를 해보려고 하였지만

그나마 가장 빠르고 쉽게할수 있는 opencv-python 예제를 선택해서 빠르게 훑어가는 중이다.

이전에도 opencv 예제들을 몇번 해본적은 있으나 c++에서만 해봤고

대강 흐름 로직은 알겠지만

지금 opencv-python에서 하는것 이미지 프로세싱, 특징, 영상, 머신러능 등 만큼 잘 체계화 되어있지는 않았었다.

그런 이유로 이번주 초에 시작하여

프로토타이핑, 대학수학, 확률론과 병행하면서

OPENCV 소개, GUI 프로그래밍, 기본 연산, 이미지 프로세싱 부분까지 오게되었다.

지금까지 한것만해도 다른 과목들과 같이 병행한것 치고는 많이 오긴했다.

GUI 프로그래밍 연습 많이 안됬었는데 기능도 한번 둘러보고,

특히 그라디언트, 푸리에변환, 허프변환 탬플릿 매칭, 웨터 셰드 알고리즘을 이용한 영상 분할 등은 

이전에 공부했을때는 제대로 보지 못했지만 그래도 정리하면서 많은 도움이 되었다.

다른 학문들은 대충대충 하면 금방 끝낫던 반면에

opencv-pythonn은 내 나름대로는 빠르게 한다고는 했지만 아직까지 할게 너무많이 남아있다.

여전히

- 특징 검출과 기술자

- 영상 해석

- 카메라 캘리브레이션과 3차원 복원

- 머신러닝

위 와같이 많은 주제가 남아있다보니

이번주 중으로 끝내기는 힘들것 같더라.

그래서 생각을 정리해보고자 이렇게 글을 쓰고 있다.

다음주부터는 주미 파워유저 발표 자료랑

프로토 타이핑에 전념해야하는만큼

이번 주말 중에 opencv 전반을 마무리하기를 희망하고 있다.

일단 피처가 무엇인지는 알고 있으니

피처 검출 부분은 대부분 간단히 넘어가고자한다.

넘어가고자 했으나

그래도 대표적인 특징인 SIFT, SURF는 물론

Fast, BRIEF, ORB 특징도 짚고 넘어가야겠다.

그동안 공부한 내용을 정리하면

SIFT와 서프는 회전, 평행이동과 스케일 변화에 강인한 특징으로 알고있다.

하지만 FAST는 회전, 평행이동에는 강인하나 스케일에는 강인하지 못한것으로 알고

브리프는 회전 변환에 강하고,

ORB는 FAST와 브리프의 조합으로 알고있다.

내가 이해하는 특징에 대한 내용은 이정도로

대가 위에서 말한 특징들 전반과 특징 전반을 오늘 6시 이전까지 마무리하면 많이 진행될것 같다.

오늘 저녁시간에는 비디오 해석과 카메라 캘리브레이션 정도 내용을 갈수있으면 좋겟다.

원래 더 나아가면 물체 검출 부분이 있는데

도저히 하르케스케이드가 잘 이해되지않는다

하르가 유사 하르 커널을 조합하여 여러 하르특징을 만들어내고

케스케이드라고 하는 약분류기들의 모음을 통해 얼굴 부분을 검출한다 정도로 개념은 알고 있지만

이거에 대해 그렇게 시원하게 알고있지는 않다.

직접 케스케이드 분류기에 대해서 정의하고 다양한 훈련을 겪어봐야할지

이를 어떻게 다루어야 될지는 이번 주말에 하기는 벅잘것 같다.

여유가 된다면 머신러닝과 함께 이 내용을 정리해보려고 한다.

일단 오늘 중으로 특징 검출, 비디오 해석, 스테레오 비전 등 내용을 할수 있으면 좋겠다.

컴퓨터 비전을 다다루려고 하는데 1주일 안에 시간을 쪼개서 하자니 너무 벅차긴한데

한번이라도 이렇게 돌려본데에 의의를 두자

이전에 비주얼 오도메트리 연습을 할떄

지금 만큼의 백그라운드 지식이 없이 하다보니

오도메트리 조차 제대로 검출해보지도 못하고 남의 예제에서 대충해보고 마무리했다.

그래도 지금이라면 동내 영상을 찍고 어느정도 할수있을것 같은 기분이 들기도 하다.

비주얼 오도메트리와 백엔드 최적화까지 어느정도 다룰수있으면 좋겟다 ㅠㅜ

이론

- 흑백 이미지를 토폴로지로 볼수 있는데, 고 강도 부분은 언덕, 저 강도 부분을 계곡이라 볼수 있습니다. 이제 고립된 계곡 부분(지역 최소점)에 다른색의 물(라벨)이 차있다고 해봅시다. 물이 차면서 언덕이 어떻게 되있느냐에 따라 물이 섞이게 됩니다. 이런 현상을 막으려면 물이 석기는 지점에 장벽을 만들어야 되는데요. 물이 언덕에 찰때까지 물을 더붇고 장벽을 더 지어봅시다. 그렇게 만든 장벽이 분할한 결과라 할수 있겠습니다.

 => 이것이 워터셰드 방법의 기본 개념이 되겠습니다.

- 하지만 노이즈 때문에 너무 과하게 분할될수도있어요. 그래서 OpenCV에선 마커기반 워터세드 알고리즘이 있는데, 지정한 계곡점부분은 합쳐지거나 합쳐지지 않게도 할수 있어요 

일단 위 동전 이미지에서 오츠 알고리즘으로 이진화 부터 해봅시다.

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('coins.png')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray,0,255,cv2.THRESH_BINARY_INV+cv2.THRESH_OTSU)

cv2.imshow("ret", ret)
cv2.waitKey(0)
cv2.destroyAllWindows()

- 이제 이진화 결과중에 아직 흰색 작은 노이즈가 약간식 존재하게 되는데 이를 모폴로지 열림 연산으로 없앨수 있습니다. 작은 점들을 제거하고 나선 모폴로지 닫힘 연산을 진행하겠습니다. 그렇게 해서 물체의 중심 위치와 배경 위치를 파악할수 있게 되지만 아직은 동전들사이 경계선은 알수 없습니다. #noise removal

- 이제 확실히 동전인 영역들을 추출해내야되는데요. 여기서 침식 연산으로 경계 픽셀들을 제거하겠습니다. 그러면 동전이 서로 닫지 않는경우에 확실히 동전인걸 알수 있겠지만 여기 있는 동전들을 서로 붙어있기 때문에, 거리 변환을 수행한후 적절한 임계치로 찾는게 좋은 방법이 되겠습니다. # find sure foreground area

- 다음으로 확실히 동전이 아닌 공간을 찾아보겠습니다. 이 경우 팽창을 하여 얻을수 있는데, 팽창은 물체의 경계를 증가시켜 실제 배경 부분을 더 잘 나타낼수 있도록 도와줍니다. #sure background area

- 확실히 배경인 부분과 확실히 물체인 부분들 이외의 공간을 구하려면 sure_fg - sure_bg 로 얻을 수 있습ㄴ디ㅏ.

- 아래의 이진화 결과 이미지를 보면 붙어있지만 동전들의 위치를 알수 있게 되었습니다. 여기까지 내용이 붙어있는 물체들간의 분할이었고, 물체 분할을 하고자 한다면, 거리 분할을 할 필요없이 침식 연산이면 충분하여 앞에 존재하는 물체들끼리 나눌수 있게 됩니다.

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('./res/coins.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray,0,255,cv2.THRESH_BINARY_INV+cv2.THRESH_OTSU)


# noise removal
kernel = np.ones((3,3),np.uint8)
opening = cv2.morphologyEx(thresh,cv2.MORPH_OPEN,kernel, iterations = 2)

# sure background area
sure_bg = cv2.dilate(opening,kernel,iterations=3)

# Finding sure foreground area
dist_transform = cv2.distanceTransform(opening,cv2.DIST_L2,5)
ret, sure_fg = cv2.threshold(dist_transform,0.7*dist_transform.max(),255,0)

# Finding unknown region
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg,sure_fg)


plt.subplot(131),plt.imshow(sure_bg, cmap="gray")
plt.title("sure background")
plt.subplot(132),plt.imshow(dist_transform, cmap="gray")
plt.title("distance transform")
plt.subplot(133),plt.imshow(sure_fg, cmap="gray")
plt.title("sure foreground")

plt.show()

- 이제 코인들의 위치를 알수 있게되었고 어디까지가 배경인지도 알게 되었습니다. 이제 마커를 생성하고 그 마커 공간에 라벨을 붙이겠습니다. 이 영역은 확실히 배경인지 물체인지 알수 있는 것들로 서로 다른 양의 정수값들을 주겠습니다. 배경에는 0을주고,다른 물체는 1에서 부터 라벨을 붙이기 시작하겠습니다.

- 하지만 배경이 0으로 준다면, 워터셰드는 모르는 공간으로 판단해서 동작하게 될겁니다. 그래서 배경도 마킹하려면 다른 정수를 써야됩니다. 

=> 배경은 원래 0이나 1로 하고, 다른 물체들은 1 이하의 정수, 모르는 부분은 0으로 마킹

# Marker labelling
ret, markers = cv2.connectedComponents(sure_fg)

# Add one to all labels so that sure background is not 0, but 1
markers = markers+1

# Now, mark the region of unknown with zero
markers[unknown==255] = 0

- 마커는 준비되었으니 워터 셰드를 하겠습니다.  경계 영역은 -1로 마커되니 빨간색으로 칠하겠습니다.

markers = cv2.watershed(img,markers)
img[markers == -1] = [255,0,0]

- 정리

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('./res/coins.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray,0,255,cv2.THRESH_BINARY_INV+cv2.THRESH_OTSU)


# noise removal
kernel = np.ones((3,3),np.uint8)
opening = cv2.morphologyEx(thresh,cv2.MORPH_OPEN,kernel, iterations = 2)

# sure background area
sure_bg = cv2.dilate(opening,kernel,iterations=3)

# Finding sure foreground area
dist_transform = cv2.distanceTransform(opening,cv2.DIST_L2,5)
ret, sure_fg = cv2.threshold(dist_transform,0.7*dist_transform.max(),255,0)

# Finding unknown region
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg,sure_fg)


# Marker labelling
ret, markers = cv2.connectedComponents(sure_fg)

# Add one to all labels so that sure background is not 0, but 1
markers = markers+1

# Now, mark the region of unknown with zero
markers[unknown==255] = 0

markers = cv2.watershed(img,markers)
img[markers == -1] = [255,0,0]

plt.subplot(121),plt.imshow(markers)
plt.title("marker image after segmentation")
plt.subplot(122),plt.imshow(img)
plt.title("result")
plt.show()

'

허프변환

- 간단히 말하면 직선 검출 알고리즘

- x-y 좌표계상에 존재하는 점들을 극 좌표계상의 직선으로 변환

- 극 좌표계상 이 직선들의 교점이 이미지의 직선

import cv2
import numpy as np

img = cv2.imread('./res/dave.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)

lines = cv2.HoughLines(edges,1,np.pi/180,200)
for line in lines:
    rho = line[0,0]
    theta = line[0,1]
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a*rho
    y0 = b*rho
    x1 = int(x0 + 1000*(-b))
    y1 = int(y0 + 1000*(a))
    x2 = int(x0 - 1000*(-b))
    y2 = int(y0 - 1000*(a))
    cv2.line(img,(x1,y1),(x2,y2),(0,0,255),2)

cv2.imshow("img", img);
cv2.waitKey(0);
cv2.destroyAllWindows();
#cv2.imwrite('houghlines3.jpg',img)

확률론적 허프 변환

- 확률적 허프 변환은 허프 변환의 최적화 기법중 하나

- 확률적 허프 변환에서는 모든 점을 고려하지 않고, 직선 검출에 충분한 임의의 점들의 부분 집합을 사용

- 아래와 같이 허프 공간 상에서 모든 점이 아닌 일부만 존재, 대신 임계치를 줄임.

import cv2
import numpy as np

img = cv2.imread('./res/dave.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)
minLineLength = 100
maxLineGap = 10
lines = cv2.HoughLinesP(edges,1,np.pi/180,100,minLineLength,maxLineGap)
for line in lines:
    x1 = line[0,0]
    y1 = line[0,1]
    x2 = line[0,2]
    y2 = line[0,3]
    cv2.line(img,(x1,y1),(x2,y2),(0,255,0),2)

#cv2.imwrite('houghlines5.jpg',img)
cv2.imshow("img", img);
cv2.waitKey(0);
cv2.destroyAllWindows();

허프 변환을 이용한 원 검출

- 원은 수학적으로 아래와 같이 표현

- 위 식에서 3개의 파라미터 x_center, y_center, r을 구하려면 3D 누적기가 필요한데, 대신 opencv에서는 에지의 경사 정보를 이용한 허프 그라디언트 방법이 있습니다.

- cv2.HoughCircles()함수로 원 검출하는 예제는 아래와 같습니다.

import numpy as np
import cv2

img = cv2.imread('./res/opencv_logo.png',0)
img = cv2.medianBlur(img,5)
cimg = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)

circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,20,
                            param1=50,param2=30,minRadius=0,maxRadius=0)

circles = np.uint16(np.around(circles))
for i in circles[0,:]:
    # draw the outer circle
    cv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)
    # draw the center of the circle
    cv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3)

cv2.imshow('detected circles',cimg)
cv2.waitKey(0)
cv2.destroyAllWindows()

탬플릿 매치

- 팀팰릿 매칭은 큰 이미지에서 탬플릿 이미지의 위치를 찾아내는 방법이라 할수 있습니다.

- opencv에선 cv2.matchTemplate()이란 함수를 제공하고있는데요. 단순히 탬플릿 이미지를 2차원 컨볼루션처럼 슬라이드하고, 탬플릿과 이미지 일부(이미지와 탬플릿이 겹친 부분)를 비교 한다고 할수 있겠습니다.

- 여기서는 탬플릿과 이웃한 픽셀들로 이루어진 흑백 영상을 반환하게 됩니다.

- W x N 크기의 입력 영상과 w x h 크기의 탬플릿 영상이 주어지면, W-w+1, H-h+1 크기의 출력 영상이 나오게 되는데 여기서 cv2.minMaxLoc()함수로 왼쪽위 코너점의 좌표와 영역의 폭과 높이를 반환해 줍니다. 이 사각 영역이 탬플릿의 공간이라 할수 있겠습니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/messi.jpg',0)
img2 = img.copy()
template = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/template.jpg',0)
w, h = template.shape[::-1]

# All the 6 methods for comparison in a list
methods = ['cv2.TM_CCOEFF', 'cv2.TM_CCOEFF_NORMED', 'cv2.TM_CCORR',
            'cv2.TM_CCORR_NORMED', 'cv2.TM_SQDIFF', 'cv2.TM_SQDIFF_NORMED']

for meth in methods:
    img = img2.copy()
    method = eval(meth)

    # Apply template Matching
    res = cv2.matchTemplate(img,template,method)
    min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(res)

    # If the method is TM_SQDIFF or TM_SQDIFF_NORMED, take minimum
    if method in [cv2.TM_SQDIFF, cv2.TM_SQDIFF_NORMED]:
        top_left = min_loc
    else:
        top_left = max_loc
    bottom_right = (top_left[0] + w, top_left[1] + h)

    cv2.rectangle(img,top_left, bottom_right, 255, 2)

    plt.subplot(121),plt.imshow(res,cmap = 'gray')
    plt.title('Matching Result'), plt.xticks([]), plt.yticks([])
    plt.subplot(122),plt.imshow(img,cmap = 'gray')
    plt.title('Detected Point'), plt.xticks([]), plt.yticks([])
    plt.suptitle(meth)

    plt.show()

탬플릿 매치로 다중 물체 검출하기

- 이전 장에서는 메시 얼굴을 찾아냈다면 이번에는 다중 물체를 검출하겠습니다. 

- 이번과 같이 다중 물체 검출의 경우 cv2.minMaxLoC()는 모든 물체의 위치를 알려주지 못하므로 이번에는 임계화를 통해 마리오 게임에서 코인들을 찾아내겠습니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img_rgb = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/mario.png')
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_BGR2GRAY)
img_rgb = cv2.cvtColor(img_rgb, cv2.COLOR_BGR2RGB)
template = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/mario_coin.png',0)
w, h = template.shape[::-1]

res = cv2.matchTemplate(img_gray,template,cv2.TM_CCOEFF_NORMED)
threshold = 0.8
loc = np.where( res >= threshold)
for pt in zip(*loc[::-1]):
    cv2.rectangle(img_rgb, pt, (pt[0] + w, pt[1] + h), (0,0,255), 2)

plt.imshow(img_rgb)
plt.show()
#cv2.imwrite('res.png',img_rgb)

푸링에 변환은 여러가지 필터의 주파수 특성을 분석하는데 필요합니다.

영상의 경우 2D 이산 푸리에 필터 (DFT)를 주파수 영역에서 분석하기 위해서 사용하는데요.

고속화된 알고리즘을 Fast Fourier Transform FFT라고 부르기도 합니다.

푸리에 변환에 대한 자세한 내용은 생략하고 우선 넘파이에서 사용해봅시다.

1. 넘파이에서 푸리에 변환

- 넘파이의 FFT 패키지에서 np.fft.fft2()함수로 주파수 영역으로 변환을 할수 잇습니다.

- 첫번째 매개변수는 흑백 이미지, (옵션) 둘쨰 매개변수는 출력 사이즈가 됩니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/home.jpg',0)
f = np.fft.fft2(img)
magnitude_spectrum = 20*np.log(np.abs(f))

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

- 아래의 이미지를 보시면 0 주파수 요소(DC 요소)는 왼쪽 위 코너에 있는걸 볼수 있는데요. 이들을 np.fft.fftshift()함수로 중앙으로 이동시킬수 있습니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/home.jpg',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))


plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

- 이제 저주파수 영역대가 중앙으로 모였습니다. 주파수 영역에서는 다양한 연산을 수행할수 있는데, 고주파 필터를 통과시킨후 역 이산 푸리에 변환으로 이미지를 복원시킬수가 있겠습니다.

- 여기서 저주파 영역은 60 x 60 크기의 윈도우로 제거하고, np.fft.ifftshift()로 다시 DC요소를 왼쪽 위 원래 자리로 돌려줍시다. 그러고나서 역 FFT함수로 되돌려주면 되겠습니다.

- 위 이미지는 고주파 통과 필터로 에지 검출 연산을 한 결과를 보여주고  있는데요. 이영상이 이미지 그라디언트에서 본것과 동일한거라고 할수 있겠습니다.

2. opencv 푸리에 변환 - 저주파 통과 필터

- 이전 장에서는 고주파 통과 필터를 사용해서 저주파 요소들을 제거하였다면, 이번에는 opencv로 저주파 통과 필터를 사용하여 고주파 요소를 남겨보겠습니다. 이를 통해 이미지를 블러링 한 결과를 얻을수가 있겠습니다.

- 아까는 저주파 영역에다가 0을 주었지만 이번에는 저주파 영역을 1로 지정해서 저주파 영역들은 통과시키고 고주파 영역은 0이 되도록 하겠습니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/home.jpg',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))

rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)

# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

1. 흑백 이미지 히스토그램 출력

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/home.jpg',0)

plt.subplot(121),plt.imshow(img, cmap="gray")
plt.subplot(122),plt.hist(img.ravel(),256,[0,256]);

plt.show()

2. 컬러 이미지 히스토그램 출력

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/home.jpg')


color = ('b','g','r')
for i,col in enumerate(color):
    histr = cv2.calcHist([img],[i],None,[256],[0,256])
    plt.plot(histr,color = col)
    plt.xlim([0,256])
plt.show()

3. 비트와이즈 연산으로 마스킹

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('C:/Users/do/Documents/github/opencv_python/res/home.jpg',0)

# create a mask
mask = np.zeros(img.shape[:2], np.uint8)
mask[100:300, 100:400] = 255
masked_img = cv2.bitwise_and(img,img,mask = mask)

# Calculate histogram with mask and without mask
# Check third argument for mask
hist_full = cv2.calcHist([img],[0],None,[256],[0,256])
hist_mask = cv2.calcHist([img],[0],mask,[256],[0,256])

plt.subplot(221), plt.imshow(img, 'gray')
plt.subplot(222), plt.imshow(mask,'gray')
plt.subplot(223), plt.imshow(masked_img, 'gray')
plt.subplot(224), plt.plot(hist_full), plt.plot(hist_mask)
plt.xlim([0,256])

plt.show()

목표

- 이미지 피라미드에 대해서 배워봅시다

이론

- 일반적으로 상수 크기의 이미지를 사용합니다. 하지만 같은 이미지이지만 다른 해상도들이 필요한 경우가 있는데요. 이미지에서 무언가를 찾을때, 얼굴과 같이 크기를 모르는 경우가 있을겁니다.

- 이 경우에는 이미지를 여러 해상도로 만들어놓고 모든 이미지에서 물체를 탐색하는 방법을 사용합니다. 이러한 다양한 해상도에서 이미지들을 이미지 피라미드라 부르는데, 가장 큰 이미지는 바닥, 가장 작은 이미지는 꼭대기에 있습니다.

- 이런 이미지 피라미드에는 2가지 종류로 가우시안 피라미드와 라플라시안피라미드가 있겠습니다.

- 가우시안 피라미드에서 가장 높은 층(저 해상도)는 고해상도 이미지에서 일부 행과 열을 지우면서 만들게 되는데, M x N 크기의 이미지들이 M/2 x N/x 크기가 됩니다. 

import cv2
import numpy as np

img = cv2.imread("C:/Users/do/Documents/github/opencv_python/res/kimheungkook.jpg")
lower_reso1 = cv2.pyrDown(img)
lower_reso2 = cv2.pyrDown(lower_reso1)


cv2.imshow("img", img);
cv2.imshow("lower_reso1", lower_reso1);
cv2.imshow("lower_reso2", lower_reso2);

cv2.waitKey(0);
cv2.destroyAllWindows();

목표

- 캐닝 에지 컨샙 배우기

- cv2.Canny()함수 배우기

이론

- 캐니 에지 검출기는 많이 사용하는 에지 검출 알고리즘으로 196년 존 F 캐니가 만들었습니다. 이 캐니 에지 알고리즘은 여러 단계로 구성된 알고리즘으로 다음과 같습니다.

1. 노이즈 제거

- 에지 검출기는 어느정도 노이즈에 강인해야 하기때문에 첫 단계에서는 5 x 5크기의 가우시안 필터로 노이즈를 제거합니다. 이에 대해서 이전에 봤으니 넘어가겠습니다.

2. 이미지의 그라디언트 강도 계산하기

- 노이즈가 제거된 이미지는 그 다음에 소벨 커널로 수평과 수직 방향으로 필터를 적용하고 수평 방향에 대한 1차 미분 영상과 수직 방향에 대한 1차 미분 영상을 얻습니다.

- 이 두 영상을 가지고 에지 그라디언트와 방향을 얻을수 있게 됩니다

- 그라디언트 방향은 항상 에지에 수직이며, 수직, 수평 그리고 두 대각 방향 중 하나를 의미하는 값이라 할수 있겠습니다.

3. 비최대 억제 - non-maximum suppression

 그라디언트의 크기와 방향에 대한 정보를 얻으면 이제, 에지가 아닌 픽셀들을 제거하여야 합니다.

- 이 때, 모든 픽셀들은 그라디언트의 방향에 존재하는 이웃 점들과 비교하여 지역 최대점인지 확인하여야 합니다.

- 아래의 그림에서 A는 에지로(수직 방향에 대한), 그라디언트 방향은 에지와 돌일 합니다. 

- B,C는 그라디언트 방향에 존재하는데, 점 B, C가 지역 최대점인지 확인여야 하고 아닌 경우들은 0으로 놓습니다.

4. 가정 임계화 hysteresis Thresholding

- 이번 단계에서는 모든 에지가 실제 에지인지 아닌지 판단하여야 합니다. 여기서는 최소, 최대를 나타내는 임계값을 사용하겠습니다. 어느 에지가 maxVal보다 크면 에지, minVal보다 작으면 에지가 아니므로 버립니다.

- 이 두 임계치 사이에는 연결성을 이용해서 에지 여부를 판단하는데요. 사이에 존재하는 픽셀들이 확실히 에지인 것과 연결되어있다면 에지의 일부분으로 판단하고, 연결되지 않았다면 버리게 됩니다.

- 위 그림의 경우 에지 A는 최대값을 넘어가므로 확실한 에지가 됩니다. 에지 C의 경우에는 최대 값보다 밑에있으나 A에 연결되어 있으므로 이 또한 에지라고 판단합니다. 

- 하지만 에지 B의 경우 최소값은 넘어가지만 확실히 에지인것과 연결되어있지 않으므로 버립니다. 그래서 최대 최소 임계치를 잘 결정해야 올바른 결과를 얻을수가 있겠습니다.

케니 에지 검출기

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread("C:/Users/do/Documents/github/opencv_python/res/kimheungkook.jpg",0)
edges = cv2.Canny(img,100,200)

plt.subplot(121),plt.imshow(img,cmap = 'gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])

plt.show()