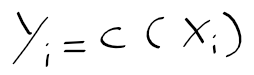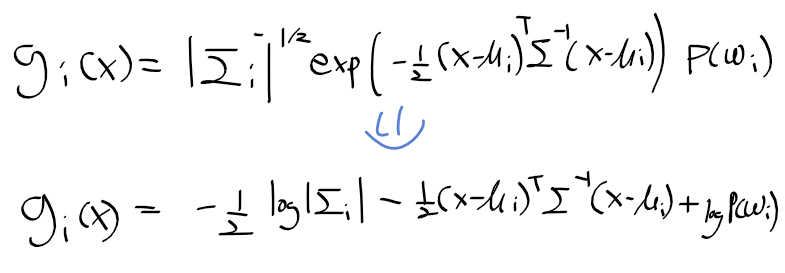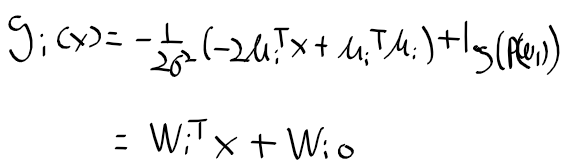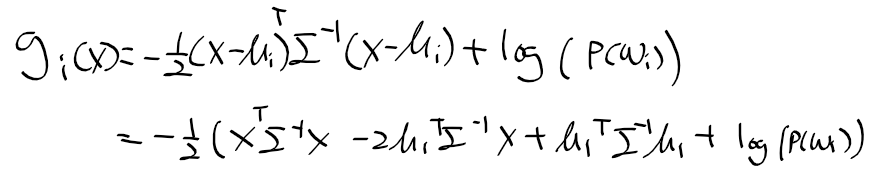1. 데이터 마이닝 개요
데이터 마이닝
- 데이터로부터 의미있는 정보를 추출하는 학문
- ex. 벡터 양자화, 클러스터링
패턴인식 시스템의 학습 과정
- 지도 학습 supervised learning이나 비지도학습 unsupervised learning으로 수행함.
- 지도 학습 : 특징벡터 x와 클래스 omega가 같이 주어진 상황에서의 학습
- 비지도학습 : 특징 벡터 x = {x1, ..., xn}만으로 이루어진 데이터로 수행한 학습
- 클러스터링 : 정답(클래스)가 정해지지 않은 데이터들을 적절하게 분류하여 모아주는 방법
비지도 학습의 장점
- 표본이 너무 많아서 라벨링 하기 힘든 경우
- 특징 벡터에 클래스 라벨이 주어지지 않았을 때
- 표본들이 작은 프로토타입 원형들로 분류될수 잇을때
2. 비지도 학습에 관하여
비지도 학습의 방법들
- 모수적 혼합 모델 구축하는 방법과 비모수적 방법 2가지가 존재
모수적 혼합 모델 구축을 통한 비지도 학습
- 여러개의 확률 밀도 함수로 주어진 클래스 데이터를 모델링
- 아래의 식과 같이 수학적 모델링 수행하며 혼합 모델이라 부름
비모수적 방법
- 데이터가 어느 확률 밀도 함수를 따른다는 가정 없이, 즉 파라미터 없이 정해진 클래스 수 만큼 데이터를 나누는 과정
- 대표적으로 k-means 클러스터링 알고리즘이 존재 => 최적화 기법으로 EM 알고리즘 사용.
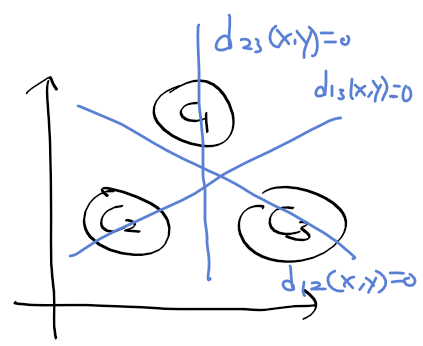
3. 벡터 양자화
벡터 양자화 vector quantization와 클러스터링 clustering의 의미
- 벡터 양자화 = 클러스터링. 둘이 동일한 뜻
- 벡터 양자화 : 특징벡터 집합 x = [x1, ..., xn]를 K개의 특징 백터 집합 y = [y1, ... yk]로 사상
=> 사상 함수 y_i = c(x_i)가 정의됨.
* c( )는 양자화 연산자
* y_i는 코드 벡터, 코드 워드, 클러스터라 부름
* y는 코드 워드(클러스터)들의 모임인 코드북이라 함.
- 클러스터의 갯수 : 코드북의 크기
=> n개의 특징 벡터 데이터들을 K개의 클러스터로 분류하는것이 벡터 양자화(클러스터링)
- 클러스터 중심점 센트로이드 centroid : 특정 클러스터에 소속한 특징 벡터들의 중심점
- 코드 북의 크기 K는 미리 정해져 있어야함
- 아래으 그림은 kmeans 클러스터링 예시
https://dashee87.github.io/data%20science/general/Clustering-with-Scikit-with-GIFs/
4. 최적화의 필요성
양자화 오차의 발생
- 특징 벡터 집합 x를 새 클러스터 집합 y로 양자화 하는 중 오차 발생
- 벡터 양자화는 특징벡터들 간의 거리 척도가 많이 사용됨. 특징 공간에 맞는 척도 사용 필요
=> 대표적으로 유클리디안 거리가 가장 많의 사용
- x, y 사이의 유클리디안 거리를 다음과 같이 정의
최적화 방향
- 특징 벡터 하나 xn와 중심점 centroid c(x) 사이의 거리가 최소가 되도록 최적화 수행 필요
- 중심점의 좌표는 해당 클러스터에 속하는 모든 특징 벡터들의 평균
평균 왜곡 mean distortion
- 유클리디안 거리로 구한 오차들의 총합 . 평균 왜곡은 아래와 같다.
코드 벡터 집합 구하기의 문제
- 평균 왜곡을 최소화 하는 코드 벡터 집합 y를 어떻게 구할것인지 최적화 과정을 사용 필요
벡터 양자화의 문제와 제안된 알고리즘
1. 코드북 설계 : 주어진 데이터 집합에 최적의 코드북 찾기 => Kmeans 알고리즘
2. 양자화 : 주어진 데이터에 가장 가까운 코드벡터 찾아야함 => 비균일 이진 분할
3. 코드 워드 거리 : 주어진 벡터에 가장 가까운 워드 찾기 => kmenas 알고리즘에 따르는 이진분할 알고리즘
5. k-means, EM 알고리즘
EM 알고리즘 Expectation Maximization
- 숨겨진 정보를 가진 문제로부터 최적해를 찾는 유용한 알고리즘
=> 최적의 코드 벡터들 centroids가 클러스터들의 중심이 될 것
- 숨겨진 정보를 추정 expectation하고, maximization을 반복하여 최적해를 찾아내가는 과정
=> 대표적인 EM 최적화 알고리즘이 K-menas
EM 알고리즘과 K-means 알고리즘의 차이
- EM 알고리즘 : 초기값 선택이 지역적 최적해를 찾는데 가장 중요한 요소
- K-means : 아무 초기값에서 E-M 과정을 수렴할떄까지 반복
=> 임의의 중심점들에 속하는 클러스터들을 선정(E) -> 크러스터들로부터 중심점 결정(M) 반복
K-menas 알고리즘
1. 데이터 집합 x = [x1, ... , xn]이 주어지고, k개의 초기 중심 집합(코드 벡터 집합) y = [y1, ..., yk] 생성
2. Expectation : y_i에 가까운 클러스터들을 선정 => x의 모든 원소들은 y의 원소중 하나에 속하게 됨.
3. Maximization : 새로운 중심점 갱신
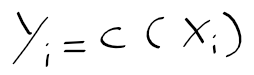
4. 총 평균 왜곡 계산
5. 총 평균 왜곡이 지정안 오차나 반복횟수가 될때 까지 2 ~ 4 반복
