패턴인식 - 4. 이차 분류기

오류확률을 최소화 하는 결정 규칙(MAP)

- MAP Maximum a Posterior 사후확률 최대화는 판별 함수로 수식화함

 

 

판별함수가 가우시안을 따르는 경우

- 공분산 행렬의 형태에 따라 데이터가 여러 형태로 분포

 

 

베이즈 분류기

- 클래스들의 데이터가 기본적으로 가우시안으로 따른다고 봄

 => 판별식이 아닌 이차형식으로 표현

 * 아래는 이차형식의 예

- 베이즈 분류기는 이차 형식으로 표현되므로 비선형(이차) 분류기라도 함.

 

 

 

 

복습) 우도비 결정규칙들에 따른 판별함수

복습) 판별식 discriminant equation

 

 

 

 

베이즈 분류기가 선형분리기가 되는 경우

- 데이터 분포(공분산)이 다음의 경우를 따르면, 선형 분류기가 됨.

1. 클래스들이 모두 가우시안 분포를 따르고, 공분산 값도 동일하며, 사전 확률이 같은 경우

   => 마할라노비스 거리 분류기

2. 클래스 모두 가우시안을 따르고, 항등 행렬에 비례하는 동일한 공분산값을 가지며, 사전확률이 같음

   => 유클리디안 거리 분류기

 

 

 

 

공분산 행렬의 종류

- 대부분의 분류기들은 베이즈 분류기인 이차 분류기로부터 유도됨.

- 아래의 그림과 같음

 

 

 

 

가우시안 확률 밀도함수 일반식

- 다변량 가우시안 확률밀도함수는 아래와 같이 정의됨

- MAP 판별함수를 구하면 다음과같음.

- 상수항을 제거하고 자연로그를 취하면 아래의 베이즈 이차 판별 함수식을 구함.

 

 

 

 

 

 

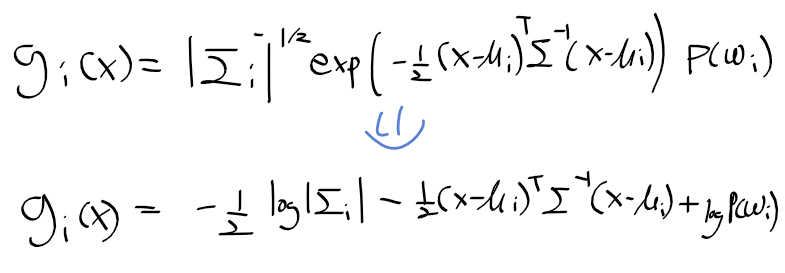
공분산이 1번 형태의 경우 판별함수 정리

- 베이즈 이차 판별 함수식의 공분산이 1번 경우와 같다면

- 특징 벡터들이 모든 클래스에서 동일한 분산 값을 가지고, 공분산이 0으로 서로 각 차원간에 독립

 => 공분산이 0이므로 제거해서 정리하자

 

-이 식을 정리하고

 

- 모든 클레스에 대해서 동일한 상수항인 x^T x 항을 제거하면, 기존의 이차 형식이던 판별함수가 일차 선형이 된다.

 => 결정 경계 decision boundaray는 g_i(x) = g_j(x)인 초평면 hyper plane임

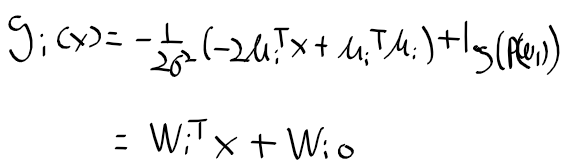
- 사전확률 P(omega_i)가 모든 클래스에서 동일한 경우 아래와 같이 판별함수는 정리됨.

 => 이를 최소 거리 minimum distance 분류기 or 최근접 평균 분류기 nearest mean 라고 함

 

 

 

 

 

 

 

 

 

 

 

최근접 평균 분류기 nearest mean classifier

- 입력되는 특징벡터와 각 클래스의 중심간 유클리디안 거리가 판별함수가 되는 간단한 분류기

 

 

- 아래의 그림은 최근접 평균 분류기로 구한 결정 경계들

 

 

 

 

 

 

 

 

 

 

 

 

공분산이 3번 형태의 경우 판별함수 정리

- i번째 공분산 행렬이 비대각 행렬 Sigma인 경우

- 이차 판별함수는 MAP 결정 기준 판별 함수로 다음과 같이 유도 및 정리 됨.

- log |Sigma|는 상수항이므로 제거하면, 마할라노비스 거리를 얻게 된다.

- Sigma = 1이면 유클리디안 거리와 마할라 노비스 거리는 동일해짐

https://www.researchgate.net/figure/Comparison-of-the-Mahalanobis-distance-x-and-the-Euclidean-distance-between-a-point-P-and_fig3_232630604

 

- 이차항을 정리하자

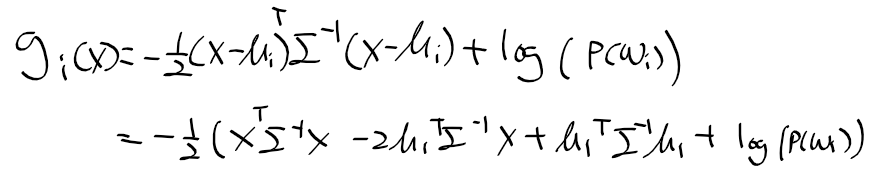
- 이차항은 상수이므로 생략하면, 이 판별 함수는 선형이 됨

 => 결정 경계는 초평면(hyper plane)이 됨.

 

- 사전 확률이 모든 i에 대해서 같담면 다음의 식을 얻음

 => 아래의 식을 마할라노비스 거리 분류기.