집밖은 위험해

용어

- 기댓값 expectation : 확률 변수 평균. 중심의미의 지표

- 분산 variance : 확률 변수의 변동성. 즉 흩어진 정도를 나타냄

- 표준 편차 standard deviation : 분산을 제곱근하여 확률 변수와 같은 단위로 표준화한것

기댓값

- 확률 분포의 중심

- 확률 변수 기댓값을 모집단 평균 \mu로 표기

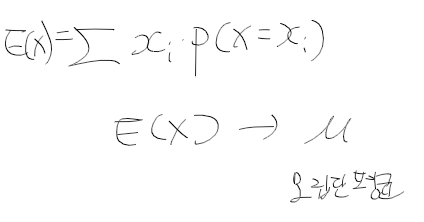
기댓값 구하기- 복권

주사위 기댓값

연속 확률 변수/ 이산 확률 변수의 기댓값

연속 확률 변수 기대값 계산 예시

분산

- 확률 변수 값들이 기댓값을 중심으로 퍼져있는정도로 \sigma^2

표준편차 standard deviation

- 분산을 제곱근하여 구함

동전을 한번 던져서 나오는 확률에 대한 분산과 표준 편차를 구하시오

주사위 눈금 변수와 분산의 표준 편차

연속 확률 변수의 분산과 표준편차를 구하라

이산 확률 분포

- 이산 균일 분포 : 이산 확률 변수 모든 값의 확률이 같은 확률 분포. ex : 동전 던지기, 주사위 던지기

- 초기하 분포 : 2개의 군으로 구성된 모집단에서 표본을 비복원 추출시 분포. ex 불량품 갯수

- 베르누이 분포 : 한 실험이 두 배반사건으로 구분될떄 사건 발생 여부에 대한 확률 분포

이산확률 변수

- 셀수있는 값인 확률 변수

- 주사위 눈, 앞/뒤, 불량품 개수

<-> 연속형

- 이산 확률 분포 : 이산 균등분포, 초기하 분포, 이항 분포, 포아송 분포

이산 균일 분포

초기하분포

- 모집단에서 표본을 비복원 추출하는 분포

-> 불량여부,  공색깔, 실패여부

- 모집단 크기 N, 표본 갯수 n, 불량 수 D 인 경우 불량품 갯수에 대한 확률 분포

초기하 분포 예제

베르누이 시행

- 실험이 두가지 서로배반인 사건 뿐일때 시행

-> 동전 앞면 뒷면, 성공/실패, 합격/불합격

베르누이 분포

이항 분포

- 베르누이 분포를 따르는 시행이 독립적으로 이루어졌을때 성공 횟수에 대한 분포

이항분포와 초기하 분포의 관게

- 초기하 분포에서 표본수가 커질수록 이항분포로 근사화됨

- 비복원 추출을 하면 초기화 분포, 복원하면 이항분포.

포아송 분포

- 이항 분포의 특이한 경우. 일정 기간동안 희귀하게 발생하는 사건 건수의 분포

- 발생 가능성 p은 매우 작으나 시행 횟수 n이 굉장히 큰 경우에 대한 확률 분포

ex. 교통사고 사망자, 희귀질병 사망자 등

잠깐 배운 통계 과정을 정리해보자

대강 생각나는대로

1. 데이터 읽기

2. 데이터 시각화

3. 데이터 분석

크게 이정도로 정리할 수 있을거같다.

데이터 분석 시 고려사항

- 보정 

- 쪼개기 

- 아웃라이어 : 아주 이상한 값

- 결측치 : 빠진 값

통계학 분류

- 기술 통계 descriptive statistics : 수집한 데이터 정리, 묘사

 -> 평균, 분산, 표준편차, 왜도(기울어진 정도), 첨도(뾰족한 정도) 

- 추론 통계 inference statistics : 수집한 데이터로 예측 함

 -> 모집단(알고 싶은 전체 집단)에서 샘플링하여 샘플링(표본) 데이터로 추론

표본 추출 기법

- SRS Simple Random Sampling, 층화, 집락, 계통, PPS

추론 통계

- 점 추정

- 구간 추정

탐색적 자료 분석

- 기술 통계 + 시각화 + 기초 통계 분석 => 전체를 탐색적 자료 분석이라 함.

데이터와 변수 구분

- 데이터 구분 : 문자형(순서형, 명목형), 숫자형

- 변수 구분 : 단변수, 이변수, 다변수

기초 통계 분석->상관관계 분석

- 산점도와 상관계수

- 변수 고려

- 비모수적 접근

상관관계 correlation

- 두변수간 연관성, 선형성, 일관성 이 얼마나 강한가

- 상관관계는 -1 ~ 1사이 값으로 0은 직선이 아님 1일수록 직선에 가까워짐

- 분석 방법 : 산점도 보기, 상관게수 보기

요인과 수준(클래스, class)

- 요인 factor : 범주형 데이터 변수(ex. 계절)

- 클래스 class : 한 요인에 존재하는 집단의 갯수(ex. 계절-4개)

문자 데이터 분석

- 카이 제곱 검정 chi sqaure test

- 정확 검정 exact test

- 트랜드 검정 trend test

카이 제곱 검정

- 교차 테이블 contingency table에 대한 검증으로 다음의 2가지 검정이 존재

  * 교차 테이블 : 두개 이상의 독립 변수끼리 눈에 보이게 한 표

- 적합도 검정 coodness of fit test : 관측 값들이 특정 확률을 따르는지 확인

- 독립성 검정 : 요인간에 연관관계 여부에 대한 검정. 독립 여부

정확 검정 exact test

- 기대도수가 작은 경우 사용.

트렌드 검정

- 독립 변수에 순위가 존재하는 경우(고도비만, 비만, 정상) 순위 증가에 따라

- 종속변수 비율 증감에 대한 경향 검정

변수 갯수에 따른 선형 회귀 분류

- 단변수 선형 회귀 : 독립 변수가 한개

- 다변수 선형 회귀 : 독립 변수가 여러개인 경우 선형 회귀

회귀 분석

- 수학적 모형을 가정하고, 이 모델로부터 데이터를 추정하는 기법

- 선형 회귀 모델은 OLS 상최소제곱법으로 만듬

다중공산성 문제

- 독립변수가 여러개인 경우 독립 변수간에 상관관계를 가지는 문제

 => 상관관계를 갖는 독립변수를 조합하여 하나로 만들거나 하나를 없앰

확률, 여사건, 오즈, 로짓, 오즈비

약과 생존 여부에 관한 오즈비

로지스틱 회귀분석

- 링크 함수 f(X) 대신 로짓을 사용한 회귀식

오즈비 구하기

- 일어날 확률에 대한 오즈/일어나지 않을 확률에 대한 오즈

전처리

로지스틱 회귀 분석기 학습 과정

- family 파라미터로 로지스틱 or 포아송 등 회귀분석기 적용

로지스틱 회귀분석 모델 해석

moonBook 라이브러리의 오즈비 플롯

- ORplot(모델) 

평가 및 교차 테이블

- ifelse로 0.5넘으면 1 아니면 0으로 판단

- table()함수로 교차 테이블 contingency table 확인

* 카이제곱 검증 -> 교차테이블 검증

caret 라이브러리의 confusionMatrix 함수

- 혼동행렬, 통계값들 출력

p value(probabilistic value)

- 유의 확률  significance probability이라고도 부름

- 귀무가설이 맞다고 가정할때 얻은 결과보다 극단적 결과가 실제 관측될 확률

- 0 ~ 1사이 값

귀무 가설 null hypothesis

- 또는 영가설이라 부르며 통계학에서 처음부터 버릴것을 예상하는 가설

- 의미없는 경우/실제 있기힘든 경우에 대한 가설

decision tree 의사결정 나무 학습법

- 트리 구조를 이용한 의사 결정 학습법

1) 어느 변수를 가장 먼저 분류해야하는가?

2) 변수 어느지점에서 분류해야할까?

- 엔트로피, 지니계수 등 활용 : 무질서도

=> 모든 변수를 평가해서 무질서도를 가장 낮출수 있는 변수를 맨위에서 분기

3) 언제까지 분류해야하는가 proning

결정트리 평가

- 트리 모델 생성 후 플로팅

- 예측 후 평가

SVM Support Vector Machine

- 마진을 가장 크게하는 분류 경계면 decision boundary을 찾음

- 2차원 보다 다차원에서 고차원 평면 hyperplnae으로 잘분할

SVM 평가

- SVM 모델로 predict 시 확률이 아니라 1, 0로 나와 중간 과정은 주석처리

- 바로 confusionmatrix로 확인

앙상블 학습법

- 머신러닝에서 완벽한 모형은 찾기 힘듬 -> 튜닝(파라미터 조절)을 해도 힘듬

- 여러 모델을 활용하여 더 개선된 결과를 획득

랜덤 포래스트

- 트리들의 집합

- 임의의 트리들을 사용

- 가장 잘 분류하는 트리들의 집합을 구함

- 평가

ROC 커브

- x축에 1- 특이도specificity, y축에 민감도 sensitivity

- 0.8 정도면 좋다.

MSE vs LSE

- MSE와 LSE를 볼때마다 수식이 똑같다보니 햇갈리곤 한다. 누가 그래서 stack overflow에 질문 글을올렷더라

- LSE는 직선과 데이터 사이 총 유클리디안 거리 최소화에 활용 => 모델 생성용

- MSE는 모델 성능 평가 지표

ref : stats.stackexchange.com/questions/146092/mean-squared-error-versus-least-squared-error-which-one-to-compare-datasets

OLS, RMS, MSE, LSE

- Ordinary Least Square : 선형 회귀 모델을 만들기 위한 선횡 최소 제곱법

- Root Mean Sqaure : 제곱 평균 제곱근 (실효값, 집단의 특성을 나타냄)

- Mean Square Error : 모델 성능 평가 지표

- Least Square Error : 모델 생성용. 거리 최소화에 사용

R 연산자

- a ~ b : b 독립변수, a 종속변수

- a$b : a데이터 프레임의 b 변수

ref : m.blog.naver.com/PostView.nhn?blogId=tjsqjavmfh&logNo=221316941091&proxyReferer=https:%2F%2Fwww.google.com%2F

geom_smooth()

- 디폴트로 국소 회귀방식 사용

 ref : m.blog.naver.com/je1206/220804412313

 ref : kuduz.tistory.com/1118

- 선형 회귀 구함

다중 공선성 문제 multicollinearity

- 독립 변수들이 상관관계가 클수록 회귀 계수 추정이 힘듬

ex)

 y: 악력의세기

 x1 : 태어난 날짜

 x2 : 나이

=> 독립 변수를 하나만 사용하던가, 조합해서 새로운 변수를 만들거나 결정을 해야함

독립변수간 상관관계가 높은지 파악하는 방법

1. 독립 변수들 간의 산점도를 그려 파악

2. 수치적인 파악 :  VIF variation inflation factor 분산 팽창 지수 혹은 Tolerance 계산하여 파악

str() 함수

- 데이터 구조 확인

선형 회귀 모델 생성

- lm(종속변수~독립변수, data= 데이터프레임)

=> speed 기울기 intercept y절편

summary() 함수

- 모델 요약

- Multiple R-sqaure : 설명 유역 => 0~1사이 값으로, 이 모델로 65% 정도 설명가능

- Adjusted R-Square 

R_j^2의 의미

- 모델에서 j번쨰 변수를 종속변수로 하였을때의 결정계수

단변수 선형회귀 모델과 다변수 선형 회귀 모델

- lm(종속변수~독립변수(+독립변수 ...),data=데이터프레임)

앞으로 해야할일

- 결과 해석 방법

- 문자 데이터 해석 방법

총 변동 SST Sum of Square of Total

- 총 변동 = 회귀 직선으로 설명가능한 변동(분산) + 회귀선으로 설명 불가 변동

  => 두 변동의 비율로 예측 변수 효과 판단

- SST = SSR + SSE

- SSR sum of square of regression : 회귀 직선으로 설명 가능한 변동

- SSE sum of square of error : 회귀 선으로 설명하고 남은 나머지 변동

결정계수 R^2

- R^2 = SSR/SST

- 추정 회귀선이 변동을 얼마나 잘 나타내는지 표현

adjusted R^2 수정 결정계수

- 다중 회귀 분석에서 독립변수가 증가시키면 결정계수가 증가하는문제의 대안으로 사용

계수 해석 방법?

- 숫자형 데이터 : x에 대한 y의 증감

- 범주형 데이터 : 기준ref을 정하여 기준값 ref에 비례 -> 더미 변수 dummy variable

더미 변수

- 범주형 변수를 연속형 변수처럼 만들며 0,1의 값을 가짐

성별 예시

- 성별 변수 gender의 값을 F, M으로 표현

1. 더미 변수로서 성별 변수 gender를 더미 변수 Female로 변환

2. Female 변수에서 1은 여성 0은 남성이 됨

계절 더미변수 해석

- 봄인 경우에 어떻더라, 여름인 경우에 어떻더라

유의성

- 변수에 대한 유의성

- 모델에 대한 유의성

=> P-value

다중 공산성 문제 해결 방법

1. 적절한 변수 선택

2. 데이터, 모델 보완

3. 추가적 관측치 구하기

변수 선택법

- 과적합 overfitting 문제로 좋은 변수들만 선택하는 것이 중요

- 1. 전진 선택법 forward selection : 가장 유의한 변수부터 하나씩 추가하는 방법

- 2. 후진 제거법 backward selection : 모든 변수로 변수만든후, 가장 유의하지 않은 변수부터 제거하는 방법

=> 문제점 : 한번 선택되면 다시 들어가거나 빠지기 힘듬

- 3. 단계적 방법 stepwise selection : 들어가거나 빠질 수 있음

로지스틱 회귀분석 logistic regression

- 선형 회귀분석에서 종속변수는 연속형 변수(키, 몸무게 등)

- 종속 변수가 변주형 범주형인 경우를 다룸(남/여, YES/NO 등)

 => 범주가 2개라면 이분형 로지스틱 회귀 분석

오즈 odds

- 일어날 확률과 일어나지 않은 확률의 비율

=> 실패에 비해 성공할 확률

베이즈 정리

- 역확률이라고 할수있음.

- 주어진 정보로 모르는 확률을 구함.

조건부 확률이란?

- 어떤 사건이 발생했다고 가정할때 다른 사건이 발생할 확률

주사위를 던질때 1이 나올 확률?

- S = {1, 2, 3, 4, 5, 6}

- A = {1}

- P(A) = 1/6

주사위를 던질때 짝수가 나올 확률

- B = {2, 4, 6}

- P(B) = 1/2

주사위 눈이 1, 2, 3 뿐이라는 정보를 알때 1이 나올 확률

- S = {1, 2, 3}

- A = {1}

=> P(A) = 1/3

주사위 눈이 1, 2, 3뿐일때 짝수가 나올 확률

- S = {1, 2, 3}

- B= {2}

=> P(B)=1/3

사건 B가 주어질때 사건 A가 일어날 확률

=> P( A | B) 조건부 확률 conditional probability

추론 방식? 확률을 다루는 두가지 관점

- 빈도론자 : 평균이 높은 사람이 우수

- 베이지안 :  조건부 확률 계산

빈도론 Frequentism, 빈도론자 Frequentist

- 빈도론적 확률론

- 사건의 빈도에 중점을 둠

베이지안 bayesian

- 사전지식의 불확실성을 다룸

- 확률을 믿음의 정도 belief of degree로 다룸

베이즈 정리

- 주어진 정보(사건 A, 사전 확률)로 또 다른 정보(사건 B일 확률, 사후 확률)을 구하는 것

- ex. A번 라인에서 불량품이 나올 확률 -> 불량이 나왔는데 A번 라인일 확률

전체 불량률

불량품이 나왔는데 B1 라인의 경우?

통계 수강생중 10%가 A학점, 비전공자중 A 받은 학생이 전체의 5%, A학점 받은 학생이 비전공자일 확률

베이즈 정리

1. 주어진 정보로 전체 확률을 구함

2. 역확률 계산

전체 인구 중 질병에 걸릴 확률, 진단 시약이 질환자 중 98% 양성, 비질환자중 90% 음성

- 진단 결과가 양성일때 질병에 걸릴 확률

- 진단 결과 음성인데 질병에 안걸렷을 확률

독립

- 사건 A에 대한 정보로 사건 B에 관한 정보를 얻을수 없음

배반

- 사건 A와 사건 B가 공통이 없는 경우

확률 변수 관련 개념

- 확률 변수 random variable : 확률 실험에서 실험을 수로 표현한 변수

- 확률 분포표 : 확률변수값에 확률을 대응한 표

- 누적확률분포함수 cumulative probability distribution funtion :확률 변수 어느값 이하로 누적하여 구한 함수

- 확률 질량함수 : 이산 확률변수(셀수 있는)의 확률 표현

- 확률 밀도 함수 : 연속 확률 변수(셀수 없는)확률 표현

ggplot

- hadley wickham 이 개발한 데이터 시각화 패키지로 가장 대중적임

- 쉬운 기능 추가

- +geom_point()과 같은 명령으로 산점도나 boxplot 등을 띄울 수 있다.

ex. geom_point, geom_line, geom_boxplot

- 색상 속성 추가 : aes(color=변수)

- 형태 지정 : aes(shape=factor(변수)

- 크기 변환: aes(size=변수)

facet_grid

- 쪼개기

geom_bar

- 바 그래프 그리기

- 막대 폭 지정 geom_bar(width=.5)

- 플립 시키기 -> x축 범주가 많은 경우 플립 시켜서 보는게 좋다.

plotly

- ggplot 결과물이 인터렉티브 반응형이 되도록 하는 패키지

연습하기

- 목표

결과

쪼개봄의 중요성

- 데이터 간 상관관계를 명확하게 파악할 수 있게 됨

tableau

- 데이터 시각화 프로그램

- 엑셀 데이터를 바로 시각화

- no coding

상관관계 분석

- 상관관계 : 두 변수사이의 선형성적 관계를 나타냄

- 공분산 : 두 변수가 같은 방향으로 움직이는 정도

- 상관계수 : 공분산을 표준편차로 나눈값

* 아웃라이어로 인해 상관계수가 크게 변동 될수 있ㅇ므

 => 아웃라이어를 잘 찾아서 제거해야함

cor 함수

- 상관관계 구함

- 숫자 데이터가 필요 -> str() 함수로 데이터 프레임 확인

- 일부 추출하여 확인한 상관관계 결과

corrplot

- corrplot 상관관계를 plot 해주는 패키지, 함수

상관관계 구분

- spearman의 상관관계 : 단조성

- 

문자형 데이터 분석 방법

- 문자형(범주형)자료 분석 -> 빈도 검정

- 카이 제곱 검정

- 정확 검정

- 트렌드 검정

카이제곱 검정 2가지

- 적합도 검정 : 관측값들이 특정 확률을 따르고 있는지 검정

- 독립성 검정 : 요인들이 서로 연관있는지 없는지 검정

- 관측값과 예측값의 차이가 클수록 연관성이 있다고 본다.

독립성 검정

- 두요인이 연관되어있는지 독립적인지 검정

- 귀무가설 H0 : 알고 있던 사실

- 대립가설 H1 : 알고자 하는 사실

카이제곱검정 

- 교차 테이블 contingency table에 대한 검정

분할표

- 분할표 contingency table or 교차표 cross tabulation 이라고도 부름

- 2개 이상 문자형 독립변수를 상호관련시켜 한눈에 보이게 한 표

자유도 degree of freedom

- 자유롭게 움직일수 있는 정도

- ex. 10개의 데이터 중 9개의 값을 알고, 평균 값을 안다. => 모르는 1개의 값이 정해짐

카이제곱 검정 수행

- chisq.test(분할표)

 => 두개의 문자형 변수 데이터에 대한 연관성을 검증

fisher의 정확 검증 exact test

- 기대도수가 5이하인 cell이 25%이상일 떄 사용.

- 카이제곱 통계량이 불안정할수 있으므로 사용

트랜드 검정 trend test

- 독립변수 순위가 있는경우 (고도비만, 비만, 정상체중 등) 순위 증가에 따라

- 종속 변수 비율이 증가/감소 경향 확인함

회귀 분석

1. 모델링 : 단변수 선형 회구, 다변수 선형 회귀

 + 다중공선성 문제(독립 변수간 영향 주어서, 연관성으로 인해 발생)

2. 모델 해석 result

 - 계수 해석 -> 표준화 계수 \beta

 - 계수의 유의성

3. 모형 설명력 result

 - 어떤 (회귀 모형) 모델이 최적의 모델인가?

 - 모형 유의성 

 - 모델 설명령

 - R^2, adjusted R^2

4. 모형 선택 selection

 - 변수선택 기법

 - 모형 비교

5. 예측 prediction

- 잔차(실제값과 예측값의 차이)와 적합치

6.1 가정체크

6.2 이상치

모형의 종류

- 수학적 모형 : input 에 대한 output 오차가 x

- 통계적 모형 : 오차를 가지고 있는 모델

회귀 분석

- 변수들의 관련성을 규명하기 위해 어떤 수학적 모형 가정

- 이 모형과 측정된 변수들을 이용하여 데이터를 추정하는 통계적 방법

- 독립변수로 종속 변수 값을 예측하는데 사용.

단순 선형 회귀 simple linear regression

- 독립변수 1개

다중 선형 회귀 분석 multiple linear regression

- 독립변수 2개

선형 회귀 모델 구하기

- lm 함수 lm(formula= y~x, data= dataframe)

 => cars 내장 데이터 사용한 결과 y절편 -17.579, 기울기 3.932

- abline(lm())으로 plot 결과에 띄울 수 있음

ls 함수

- 작업 공간 내 변수 출력

- []로 인덱싱 

plot

- 산점도로 띄우기

- x 라벨, y라벨, 타이틀 추가

-col, pch, cex: 색상 및 모양, 크기 변경

- 범위 변경 : xlim = c(최소, 최대), ylim

par 함수

- 다중 plot 함수

- mfrow로 plot 배치 설정 후 plot 함수 실행

abline

- 회귀 관련 선, 수직/수평 선

pairs

- 산점도 행렬

mycor

- pairs와 마찬가지로 산점도 행렬 plot

문북 패키지에 있는 데이터로 연습하기

- age와 height, weight, bmi 산점도

- 산점도 행렬

확률의 현재

- 불확실성을 다루기 위해 학문과 생활속에서 다양히 활용

배워야 할것들

- 확률 정의 definition of probabliistic

- 확률 분포 probabilistic distribution 특성과 계산하기

- 표본 분포 sample distribution와 확률 과정 stochastic process

- 시뮬레이션

확률을 진짜 이해하기 위해선

- 프로그램으로 돌려보는게 좋다.

- 가장 가능성 높은 결과를 예측하고 의사 결정에 활용

파스칼, 페르마와 주사위 도박

- 2명은 각각 32피스톨(화폐 단위)를 가진다.

- 3판을 이기면 승리.

- A가 2, B가 1판 이긴경우 배분

주사위 도박 승자 확률

- 일반적인 생각 : A에는 2/3, B는 1/3 

- B는 두판을 더 이겨야 하므로 B가 이길 확률 0.5 ^2 = 0.25

- A가 이길 확률 1 - (B가 이길 확률) = 0.75

- 배분 : A는 64 x 0.75, B는 64 x 0.25가 공정

=> 기댓값 : 확률 변수 평균 개념 지표

확률의 적용 범위

- 생물학, 물리학, 경제학, 통계학, 경영학, 로봇 공학 등 현대 과학 모든 분야

확률의 수학적 정의

- 어떤 사건이 일어날 가능성 0 ~ 1의 실수

- 다양한 확률의 정의들 : 상대도수적 정의, 기하학적 정의, 고전적 정의, 공리적 정의

동전 앞면이 나올 확률

- 확률 = 앞면 나온 횟수/ 전체 시행 횟수

상대도수적 확률의 정의

- n번 시행중 사건 A가 a번 발생했을때 사건 A가 일어날 확률 P(A)

- P(A) = a/n

- 100만번 동전 던져서 앞면이 나올 확률 = 500,000/1,000,000

- 야구의 타율 타석수 250, 안타수 103 => 0.412 타율 = 103/250

- 문제점 : 같은 조건에서 통계 실험을 계속 반복하기 힘듬. => 컴퓨터 시뮬레이션으로 실험 가능해짐

기하학적 확률

- 일부의 길이 또는 면적 / 공간 전체의 길이 또는 면적 => 면적의 비율

확률 구분

- 주관주의 확률 subjectivism : 몇번 시행(경험)으로 구한 확률(느낀 확률, 믿음의 정도 degree of belief)

- 객관적 확률 : 많은 시행으로 구한 확률

정의 : 수학적 정의 확률, 상대도수적 확률, 기하학적 확률

구분 : 주관주의 확률, 객관적 확률

표본 공간과 사건, 고전적/공리적/여사건 확률에 대하여

표본 공간 : 통계적 실험 모든 가능한 결과 집합

사건 : 표본 공간의 부분 집합

고전적 확률 : 사건의 원소수를 표본 공간의 원소수로 나누어 구한 확률

공리적 확률 : 고전적 확률을 일반화 시킨 확률

집합과 원소

- 집합 set : 명확하게 구분된 원소들의 묶임

- 원소 element : 구분 가능한 요소

집합의 표현

- 원소 나열법 혹은 조건 제시법으로 표현

- 원소 나열법 : A = {1, 2, 3, 4, 5}

- 조건 제시법 : A = {n은 자연수| 1<= n <= 5}

부분 집합

- 집합 B의 모든 원소가 집합 A에 속하는 경우 부분집합

- ex) A = {1, 2, 3}, B = {1} => B는 A의 부분 집합

그외 집합

- 전체 집합 U : 표본 공간

- 공집합 : 원소가 하나도 없는 집합

- 합집합 : 두 집합의 합한 집합

- 공집합 : 두 집합의 공통된 원소로 이루어진 집합

- 여집합 : 전체 집합에는 속하지만 A에 속하지 않는 집ㅎ바

- 차집합 : A - B, A에 속하나 B에 속하지 않는 집합

표본공간 S ; sample space

- 통계적 실험시 모든 가능한 결과로 이루어진 집합

- 사건 : 표본 공간의 부분 집합

동전 던지기의 표본 공간

- 앞면 H, 뒷면 T 이라 하는 경우

- S = {H, T}

고전적 확률

- 표본공간 : S = {e1, e2, .., ei, ..., ek} => n(S) = n

- 사건 : A = {e1, ..., ei} => n(A) = k

- 확률 P(A) = 사건(사상) A의 원소 개수/ 표본 공간 S의 원소 개수

              = k / n

동전 던져서 앞면이 나올 확률

- S = {H, T}

- A = {H}

- P(A) = 1/2

주사위 던져서 짝수가 나타날 확률(고전적 확률)

- S = {1, 2, 3, 4, 5, 6}

- A = {2, 4, 6}

- P(A) = 3/6 = 1/2

=> 고전적 확률 계산시에 사건 원소 개수가 중요

복원 추출

- n개 중에서 r개를 복원 추출 : n^r

비복원추출

- n개 중 r개를 비복원 추출(순서 고려) : nPr = n!/(n-r)!

- n개중 r개 비복원 추출(순서 비고려) : nCr = n!/(n-r)!r!

로또복권에서 1등에 당첨될 확률

- A = 1등 당첨

- 45C6 = 45!/6!(45-6)!

- P(A) = 1/8,145,060

공리적 확률

- 0<= P(A) <= 1

- P(S) = 1

- 탐사형 데이터 분석 eda Exploratory Data Analysis

- 데이터 종류에 따른 분석 방법

- 시각화

데이터를 다룰떄 전처리 한다고함..

전처리 + 탐사형 데이터분석 => 분석 용도에 맞게 만들어가는 과정

* 데이터 탐색이 매우 중요해짐

전처리시 확인사항

1. 중복되는 행

2. 간단히 범주화 할수 있는것 없는지 고려

 ex. 학교 계단, 학교 복도, 학교 교실 -> 모두 학교 내부로 변경 가능한지

3. 이상치 확인 

 ex. 키 554cm, 몸무게 654kg

입력된 데이터 형테에 따른 구분

- 문자형 데이터

- 숫자형 데이터

변수 갯수에 따른 구분

- 단변수 univariable

- 양변수 bivariate

- 다변수 multivariate

=> 데이터 구분에 따라 사용가능한 통계/EDA 방법이 달라짐

2개 집단

- 앞/뒤, 좌/우

2개 이상의 집단

- nomial 명목형 : 인사팀, 마케팅팀, 회계팀, 개발팀

- ordinal 순서형 : 저체중, 정상, 비만, 고도비만

* 순서형이 명목형보다 더많은 정보 가짐

숫자 형태에 따른 분류

- 연속형 : 측정 가능 ( ex. 온도, 몸무게 등)

- 이산형 : 카운팅하여 얻는 값 ( ex. 입장자 수)

open question의 목적

- 빈도 확인

- 새로운 범주 탐색

차트 

- 파이차트 : 전체적인 분포와 비율 확인 가능

- 바 차트 : 빈도 비교와 범주 간 차이를 비교 할 수 있음

- 파레토 차트 : 단순 정렬 및 누적 퍼센트 그래프

측도 measure

- mean 평균 , median 중앙값, truncated mean 절삭 평균

- var, IQR

- 왜도 첨도

Quantile 분위수

- 25%(Q1), 50%(Q2), 75%(Q3)

- 구간을 4개로 나눔

5가지 수

- min, q1, median(q2), q3, max

IQR InterQuantile Range

- Q3- Q1인 구간에 해당

- 중앙 안에 들어가는 범위를 알 수 있음

box plot

- 최대, 최소, 분위수 등 다양한 정보를 표현한 그래프

- upper/lower fence 밖은 outlier로 판단

줄기 잎그림

- 실제 데이터를 사용하여 정보 손실이 없음

- 적은 데이터를 표현에는 최적

히스토그램 histogram

-자료의 분포 상태를 직사각형으로 표현한 그래프

- 구간을 나누어 범주로 만들고 막대가 연결됨

* bar 차트는 막대 사이 간격 존재

산점도 scatter plot

- 두 개의 연속형 변수를 나타냄

- 두 변수간의 관계를 나타내는것 -> 상관관계

상관계수 correlation

- -1 ~ 1사이의 수

- 0보다 크면 양의 상관, 0보다 작으면 음의 상관관계

상관 계수 = 0의 의미

- 선형 적인 관계가 없다

- 비선형 적인 관계는 존재할 수도 있음

a <- c(1, 2, 3, 10)

# ctrl shift c 로 여러줄 주석, 취소
# mean(a)
# max(a)

# F1으로 도움말 열기
var(a)

# Visualization -----------------------------------------------------------
boxplot(a, horizontal=TRUE)
# ctrl + shfit + r로 insert section 사용 가능

getwd()




data_txt <- read.table("txt_data.txt", header=T)


head(data_txt)

names(data_txt)

summary(data_txt)

str(data_txt)

is.na(data_txt)
sum(is.na(data_txt))
colSums(is.na(data_txt))


ER_data <- read.csv("ER_exam.csv")
head(ER_data)
names(ER_data)
str(ER_data)
summary(ER_data)
colSums(is.na(ER_data))
# 데이터 전처리 필요 여부 판단 가능

install.packages("moonBook")
library(moonBook)
mytable(SEX~AGE+TEMP+AVPU,data=ER_data)

table_result <- mytable(SEX~AGE+TEMP+AVPU+F_KTAS,data=ER_data)
mycsv(table_result, file="20201019_table.csv")


mylatex(table_result)


a <- c(1, 2, 3, 10)
a
a[3]
a[2:5]

data_txt
data_txt[1,]
data_txt[,1]
data_txt[1:2,]

data_txt$age
data_txt$age[1:4]
data_txt$age>30
data_txt$age[data_txt$age>30]
data_txt[data_txt$age>30,]


#1. 나이가 30세보다 크고
#2. 성별이 M
# 이름은 data_30_M
data_txt$gender=="M"
data_txt$age>30
data_txt[data_txt$age>30, ]
(data_txt$age>30) & (data_txt$gender=="M")
data_30_M = data_txt[(data_txt$age>30) & (data_txt$gender=="M"),]
data_30_M


library(dplyr)

head(select(data_txt,starts_with("a")))
head(select(data_txt,ends_with("r")))
head(select(data_txt,contains("e")))


head(filter(data_txt, age >30))

head(arrange(data_txt,age))
head(arrange(data_txt,desc(age)))


head(mutate(data_txt,new_var=ifelse(age>=30, 1, 0)))
head(mutate(data_txt,new_var2=substr(gender, 1, 0)))


summarise(ER_data,mean_AGE=mean(AGE),mean_TEMP=mean(TEMP,na.rm=T))
summarise(group_by(ER_data,SEX),mean_AGE=mean(AGE),mean_TEMP=mean(TEMP,na.rm=T))


data_txt
data_txt %>%
  filter(age > 30) %>%
  group_by(group) %>%
  summarise(mean(age,na.rm=TRUE))

data_txt_tmp <- filter(data_txt, age > 30)
data_txt_tmp <- group_by(data_txt_tmp, group) 
data_txt_tmp <- summarise(data_txt_tmp,mean(age))
data_txt_tmp

quantile(data_txt$age,na.rm=T)

dplyr

- 데이터 매니퓰레이션 단계(전처리)

- select() 변수선택

- filter() 행선택

- arrange() 정렬

- mutate() 새변수 생성

- group by & summarise() 통계량 생성

- pipe, count, sample etc..

select(dataframe, 변수명)

- 변수에 해당하는 행 데이터 

starts_width(), ends_width(), contains()

- 변수 찾기

filter(dataframe, 비교문)

- 행 데이터 추출

- ex : filter(data_txt, age > 30)

-

arrange(dataframe, variable)

- 해당 변수 데이터 정렬

- 내림차순시 desc(변수명)

mutate

- 변수(열) 생성

- mutate(dataframe, variable name = function)

summarise()

- 통계값 산출

- summarise(dataframe, 변수명=통계함수, ...)

% (pipe 파이프)

- %>% : 흐름

- 파이프를 이용하여, 파이프 흐름을 따라 데이터프레임을 가공할 수 있다.

- %>%를 사용하지 않는 경우

 => 따로 변수 할당해서 여려줄 반복해서 만들어주어야 한다.

데이터 분석을 하려면 가장 먼저 할 일은?

-> 데이터 수집, 로딩

데이터 출력

- header =T 옵션 없으면 age, gender, group을 열이 아닌 1행으로 인식

변수 할당시 보기

- ctrl + 변수 명 클릭

head 함수

- 상위 6개 행 출력

- 데이터 상당히 많으므로 일부 볼떄 자주 사용

names 함수

- 열이름 확인하기

summary 함수

- 데이터 정리해서 출력

str 함수 (structure)

- 해당 데이터의 구조 출력

- 10개의 옵셔베이션, 3개의 바리어블

is.na 함수

- 결측치인지 반환

- is.na에 sum : true 가 1, false 는 0이며 true 가 없으므로 0이

colSums 함수

- 열 별로 sum 연산

- 아래의 예시는 각 열별 결측치 sum

read.csv()

- "tab" 쓰면 해당 wd의 파일 자동완성

- 다음 예시는 6922 옵셔베이션에 20개 변수 가짐

csv 데이터 훑어보기

- str() : 구조 파악

- summary() : 기초 통계 빈도에 대한 내용 반환

- names : 변수명 확인

- is.na() : 결측값 확인

데이터 형태

- 데이터 프레임 : 엑셀과 같은 데이터

- 스칼라 : 1 x 1 형 데이터

- 벡터 : 1 x N 형 데이터

- matrix : M x N 형 데이터

* c() : concatenate의 약어로 스칼라 값들을 연결하여 벡터로 만듬

=> ex. c(1,2,3,4,10)

R 패키지

- CRAN The Comprehensive R Archive Network

- git

moonBook 설치 및 사용

- 성별을 기준으로 AGE, TEMP, AVPU 데이터 분석

유용한 R 패키지들

support.rstudio.com/hc/en-us/articles/201057987-Quick-list-of-useful-R-packages

- 배워야할 필수 패키지 4개

- Dplyr

- ggplot2

- ggvis

- caret

latex

- 논문쓸떄 많이 사용하며, html형태로 결과를 만들어줌

데이터 프레임 일부분 추출

- 데이터프레임명[행, 열]

데이터프레임 특정 변수 접근

- 데이터프레임명$변수

- age에서 1~4 추출

- age가 30보다 큰 추출 -> true false 반환

- age가 30보다 큰 age들 추출

- age가 30보다 큰 행 전체 출력

문제

# 나이가 30세보다 크고

# 성별이 M인 사람을 뽑자