데이터분석 - 9. 회귀모형

MSE vs LSE

- MSE와 LSE를 볼때마다 수식이 똑같다보니 햇갈리곤 한다. 누가 그래서 stack overflow에 질문 글을올렷더라

- LSE는 직선과 데이터 사이 총 유클리디안 거리 최소화에 활용 => 모델 생성용

- MSE는 모델 성능 평가 지표

ref : stats.stackexchange.com/questions/146092/mean-squared-error-versus-least-squared-error-which-one-to-compare-datasets

 

 

 

OLS, RMS, MSE, LSE

- Ordinary Least Square : 선형 회귀 모델을 만들기 위한 선횡 최소 제곱법

- Root Mean Sqaure : 제곱 평균 제곱근 (실효값, 집단의 특성을 나타냄)

- Mean Square Error : 모델 성능 평가 지표

- Least Square Error : 모델 생성용. 거리 최소화에 사용

 

 

 

R 연산자

- a ~ b : b 독립변수, a 종속변수

- a$b : a데이터 프레임의 b 변수

ref : m.blog.naver.com/PostView.nhn?blogId=tjsqjavmfh&logNo=221316941091&proxyReferer=https:%2F%2Fwww.google.com%2F

 

 

geom_smooth()

- 디폴트로 국소 회귀방식 사용

 ref : m.blog.naver.com/je1206/220804412313

 ref : kuduz.tistory.com/1118

 

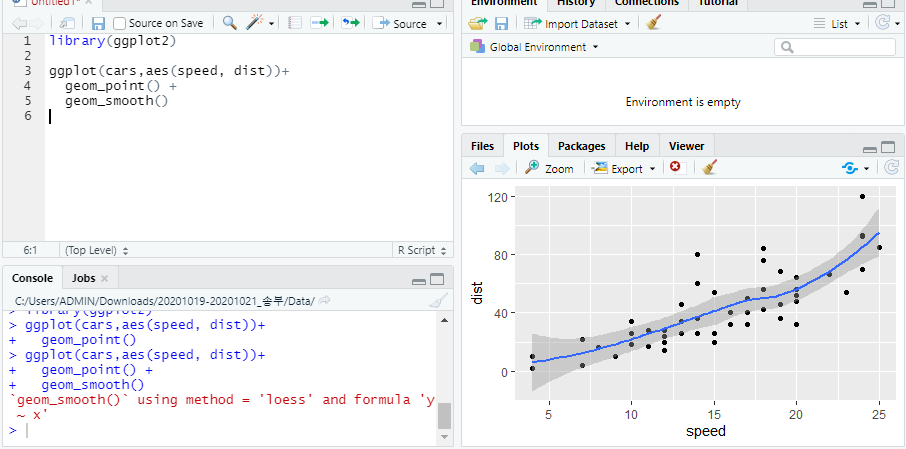
- 선형 회귀 구함

 

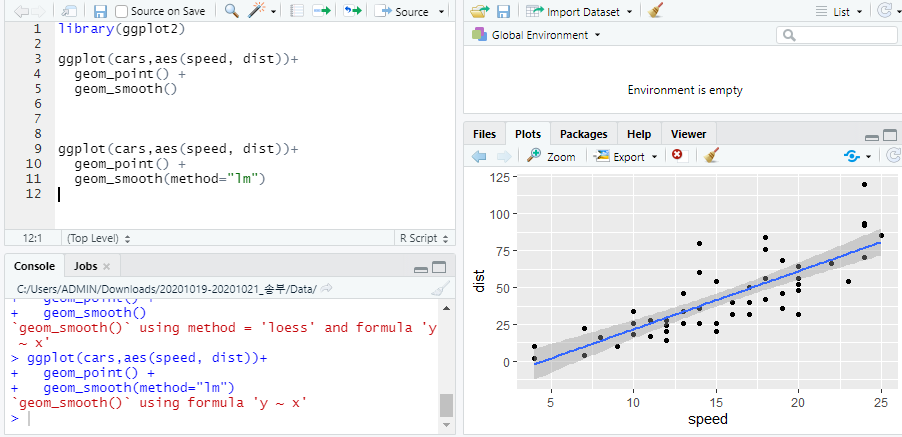
다중 공선성 문제 multicollinearity

- 독립 변수들이 상관관계가 클수록 회귀 계수 추정이 힘듬

ex)

 y: 악력의세기

 x1 : 태어난 날짜

 x2 : 나이

=> 독립 변수를 하나만 사용하던가, 조합해서 새로운 변수를 만들거나 결정을 해야함

 

 

 

독립변수간 상관관계가 높은지 파악하는 방법

1. 독립 변수들 간의 산점도를 그려 파악

2. 수치적인 파악 :  VIF variation inflation factor 분산 팽창 지수 혹은 Tolerance 계산하여 파악

 

 

 

str() 함수

- 데이터 구조 확인

 

선형 회귀 모델 생성

- lm(종속변수~독립변수, data= 데이터프레임)

=> speed 기울기 intercept y절편

 

 

 

summary() 함수

- 모델 요약

- Multiple R-sqaure : 설명 유역 => 0~1사이 값으로, 이 모델로 65% 정도 설명가능

- Adjusted R-Square 

 

 

 

R_j^2의 의미

- 모델에서 j번쨰 변수를 종속변수로 하였을때의 결정계수

 

단변수 선형회귀 모델과 다변수 선형 회귀 모델

- lm(종속변수~독립변수(+독립변수 ...),data=데이터프레임)

 

앞으로 해야할일

- 결과 해석 방법

- 문자 데이터 해석 방법

 

 

 

총 변동 SST Sum of Square of Total

- 총 변동 = 회귀 직선으로 설명가능한 변동(분산) + 회귀선으로 설명 불가 변동

  => 두 변동의 비율로 예측 변수 효과 판단

- SST = SSR + SSE

- SSR sum of square of regression : 회귀 직선으로 설명 가능한 변동

- SSE sum of square of error : 회귀 선으로 설명하고 남은 나머지 변동

 

 

 

결정계수 R^2

- R^2 = SSR/SST

- 추정 회귀선이 변동을 얼마나 잘 나타내는지 표현

adjusted R^2 수정 결정계수

- 다중 회귀 분석에서 독립변수가 증가시키면 결정계수가 증가하는문제의 대안으로 사용

 

 

 

계수 해석 방법?

- 숫자형 데이터 : x에 대한 y의 증감

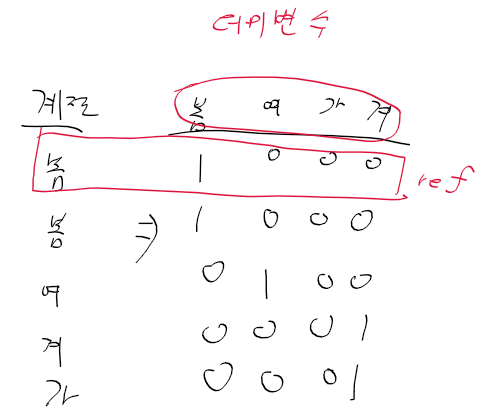
- 범주형 데이터 : 기준ref을 정하여 기준값 ref에 비례 -> 더미 변수 dummy variable

 

 

더미 변수

- 범주형 변수를 연속형 변수처럼 만들며 0,1의 값을 가짐

 

성별 예시

- 성별 변수 gender의 값을 F, M으로 표현

1. 더미 변수로서 성별 변수 gender를 더미 변수 Female로 변환

2. Female 변수에서 1은 여성 0은 남성이 됨

 

계절 더미변수 해석

- 봄인 경우에 어떻더라, 여름인 경우에 어떻더라

 

 

 

 

 

유의성

- 변수에 대한 유의성

- 모델에 대한 유의성

=> P-value

 

 

 

다중 공산성 문제 해결 방법

1. 적절한 변수 선택

2. 데이터, 모델 보완

3. 추가적 관측치 구하기

 

 

 

변수 선택법

- 과적합 overfitting 문제로 좋은 변수들만 선택하는 것이 중요

- 1. 전진 선택법 forward selection : 가장 유의한 변수부터 하나씩 추가하는 방법

- 2. 후진 제거법 backward selection : 모든 변수로 변수만든후, 가장 유의하지 않은 변수부터 제거하는 방법

=> 문제점 : 한번 선택되면 다시 들어가거나 빠지기 힘듬

- 3. 단계적 방법 stepwise selection : 들어가거나 빠질 수 있음

 

 

 

 

로지스틱 회귀분석 logistic regression

- 선형 회귀분석에서 종속변수는 연속형 변수(키, 몸무게 등)

- 종속 변수가 변주형 범주형인 경우를 다룸(남/여, YES/NO 등)

 => 범주가 2개라면 이분형 로지스틱 회귀 분석

 

 

 

오즈 odds

- 일어날 확률과 일어나지 않은 확률의 비율

=> 실패에 비해 성공할 확률