집밖은 위험해

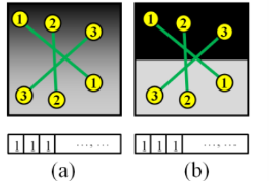
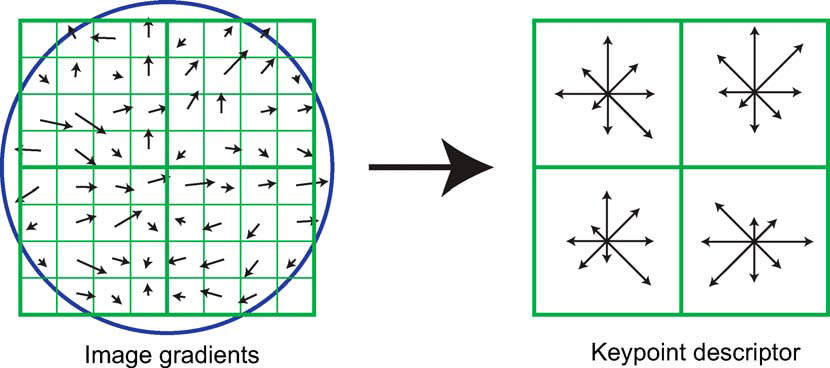
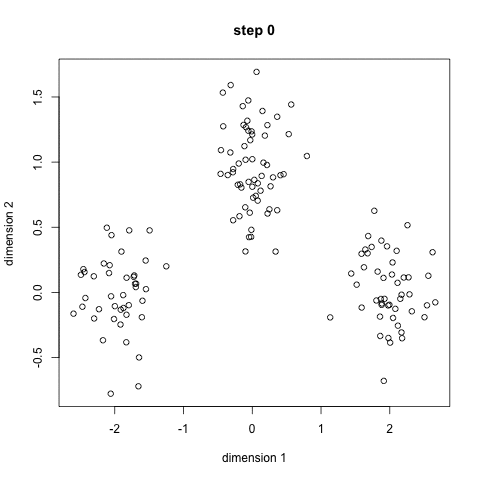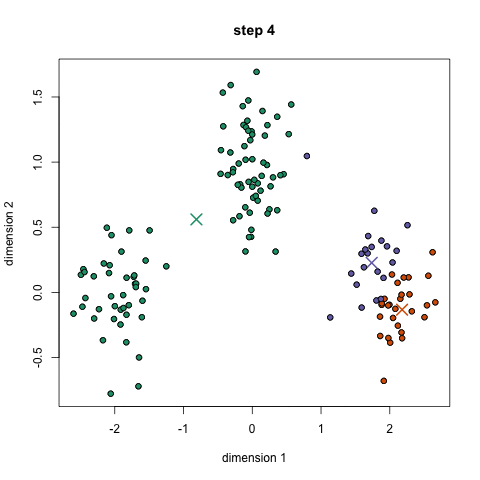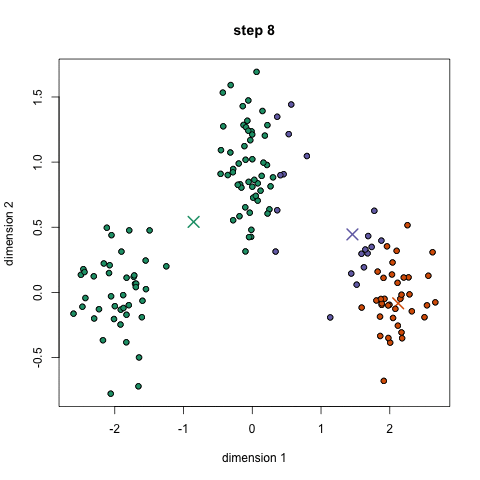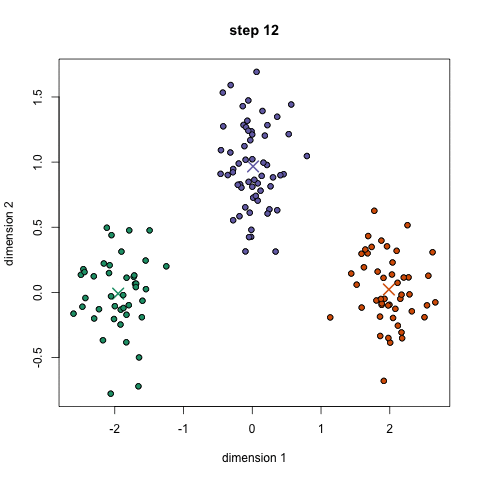
kd트리 매칭

- 지역 정보만 사용

 => 첫 영상의 특징 벡터와 둘째 영상의 특징 벡터에서 최근접 이웃을 탐색하여 대응쌍 구함

기하 변환 Geometry Transform의 예시

- 같은 물체인 다른 대응쌍이 존재시. 기하 변환은 비슷해야함

- 예시 : Rigid Transform, Affine Transform, Perspective Transform 등

kd트리 매칭과 기하 변환

- kd트리 최근접 이웃 탐색을 이용한 매칭에서는 기하 정렬 조건 고려 x, 지역 정보만 사용

=> 기하 정렬 필요

기하 정렬 알고리즘의 사용 예시

- 잡음, 가림, 섞임에도 강건한 알고리즘으로 다음들이 존재

 -> 최소제곱법(거짓 긍정이 없는 상황), RANSAC(거짓 긍정이 존재하는 경우). 상황에 맞게 적절히 사용함

- 아래의 그림은 다양한 특징에다가 기하 정렬 알고리즘을 통해 매칭한 예시들을 보여줌

최소제곱법 least square method

- 주어진 샘플들을 가장 잘 표현하는 모델을 구함

- 아래의 예시는 점 집합이 주어질때 오차가 가장 적은 직선을 구하는 그림

컴퓨터 비전에서의 최소제곱법

- 일반 최소 제곱법에서 점 집합이 주어졌으나, 컴퓨터 비전에서는 특징 집합 X가 주어짐

- 대응 쌍이 같은 물체에 존재한다면, 같은 기하 변환을 가짐.

- 기하 변환 행렬(동차 변환 행렬) : 회전, 평행이동, 크기 변환 등을 포함

- 특징의 변환 : 아래의 동차 좌표가 주어질때, 동차 좌표와 동차 변환 행렬의 곱으로 기하 변환 결과 좌표를 구함. 

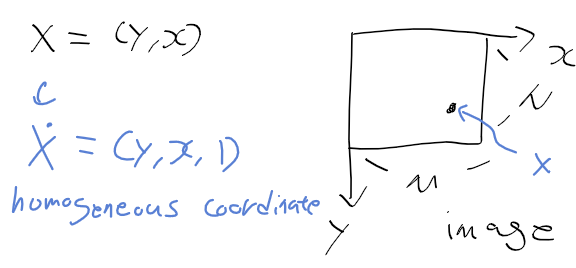
- 실제 측정한 점 b와 기하 변환을 통해 얻은 점 b' = x_dot H_dot이 주어질때,

  b와 b'의 최소 제곱 오차가 가장 줄여주는 기하 변환 행렬을 구해야 함.

최소제곱법을 이용한 매칭 예시

- 두 영상과 특징들이 주어질때, 매치 오차를 최소화 하는 기하 변환 행렬을 구한 예시

RANSAC을 이용한 매칭

- 두 영상의 특징 매칭 쌍 중에 거짓 긍정이 포함된 경우. 이를 노이즈로 보고 노이즈를 제거해야함

 => RANSAC 사용

순수 매칭 알고리즘

- 첫 영상 특징 벡터들에 대한 둘째 영상의 최근접 이웃 구함

=> 매칭쌍들을 mlist에 모음

- 아래의 그림은 이진 검색

kd트리

- 이진 검색트리의 예시

- 왼쪽 자식 노드는 기준 노드보다 작고 오른쪽 자식 노드는 기준 노드보다 큼

- 검색 키 : kd 트리에서 찾아야될 노드의 값

kd 트리 생성

- 특징

 1. 검색키는 스칼라가 아니라 벡터

 2. 검색 키에 가장 가까운 최근접 이웃 노드를 찾아야 함 

- n개의 특징벡터 X로 kd 트리를 만드는 경우, 하나의 특징 벡터 x는 d차원 벡터

- 루드 노드가 X를 두 부분 집합 X_left와 X_right로 분할

 -> 자식 노드에서도 계속 분할을 수행 => kd 노드 생성

kd 트리에서의 최근접 이웃 탐색

- 목표 : 특징 벡터 x입력이 주어질때 최근접 이웃을 찾기

- 입력 : x = (20,20)

- 과정 : 루트노드에서부터 분할해 나가며 입력에 가까운 노드를 찾아나감 -> 입력 벡터 x는 노드C에 최근접이웃

매칭 성능 판단

- 스테레오 비전과 파노라마서 여러장의 영상으로 매칭 수행

- 두 영상으로 매칭하는 경우. 첫 영상의 특징 벡터 a와 두 영상의 특징 벡터 b가 잘 매칭 => 매칭 쌍으로 판단

- 두 특징 벡터 a, b의 거리가 임계치 T보다 작으면 매칭쌍

임계치 설정하기

- T가 매우 작으면, 아주 가까운 쌍만 매칭

 => 진짜도 실패할 수 있음. 거짓 부정 FN 많이 발생

- T가 크면

 => 아닌 것도 성공함. 거짓 긍정 FP 발생

ROC Receiver Operating Charateristic 곡선

- 거짓 긍정률 FPR과 참 긍정률 TPR을 이어 만든 곡선

 => 매개변수에 따라 TP와 FP의 변화를 쉽게 보여줌

매칭 전략

- 서로 다른 영상에서 존재하는 특징이 매칭쌍인지 판단하는 방법

1. 고정 임계값 방식 : 거리가 고정된 임계값보다 작은지 확인 

2. 최근접 이웃 : 첫 영상의 특징 벡터 a가 주어질때 둘째 영상에서 최근접 벡터 b를 찾음.

3. 최근접 거리 비율 : 첫 영상 특징 벡터 a가 주어질때, 둘째 영상에서 최근접 특징벡터 b1과 다음으로 가까운 b2 취득

                      -> d(a, b1)/ d(a, b2) < T 이면 매칭

=> 최근접 거리 비율이 가장 좋은 성능을 보임

컴퓨터 비전에서의 매칭

- 서로 다른 영상간의 특징점 쌍이 동일한 것인지 확인하는 과정

- 유사성 or 거리를 측정하여 확인

 => 특징점 쌍 매칭에 거리 + 유사도 측정 척도가 필요

매칭에 사용하는 특징

- 에지

- 지역 특징

- 영역

SIFT 기술자의 거리재기

- SIFT 기술자는 128차원

- 두 점 a, b가 주어질때 이들의 거리를 측정해야함

- 방법 : 유클리디안 거리, 마할라 노비스 거리

유클리디안 거리

- 두 점 a, b가 주어질때, a와 b의 차로 구한 내적

- 유클리디안 거리가 작다 => 같은 지점을 나타낸다.

마할라노비스 거리

- 분산을 고려한 거리

- 아래의 경우 평균 mu와 점 b, 점 c가 주어질때 유클리드 거리상 점 b가 가까우나 이는 노이즈

- 점 c가 점 b보다 mu에 가깝다고 봐야함

=> 마할라노비스 거리 : 공분산을 고려한 거리

얼굴 인식

- 컴퓨터 비전 분야에서 주성분 분석을 가장 잘 사용하는 경우로 얼굴 인식이 있음.

평균 얼굴

- 여러개의 얼굴에 대한 평균 영상

고유 얼굴

- 얼굴 영상에 PCA를 적용하여 얻은 고유 벡터

1) 평균 얼굴 획득

2) 입력 얼굴 영상 - 평균 얼굴

3) 공분산 행렬 취득

=> 고유 벡터와 고유값 계산

고유 얼굴 이용한 얼굴 인식

1. 원래 얼굴 벡터 x로 고유 얼굴 벡터 y 획득

2. 입력 얼굴 xi가 주어지면 고유 얼굴 yi로 변환

3. 입력 고유 얼굴 yi와 고유 얼굴 벡터 y의 원소 들 중 거리가 가장 가까운것을 검색

* 거리가 임계값이상이면 다른사람, 없는사람

주성분 분석 PCA Principal Component Analysis

- 고차원의 벡터를 정보의 손실을 줄여 저차원의 벡터로 변환하는 기술

 => 차원 축소, 변수 추출 방법으로 널리 사용됨

- 아래의 예시에서 2차원 데이터를 1차원 데이터로 변환한 예시들을 보여줌

 => 원래 데이터의 분산을 가장 잘 보존하는 축을 찾아야 함

텍스처

- 특징 추출, 영역 분할에서 많이 사용

- 영상의 질감 -> 반복되는 일정 패턴

텍스처 분석과 구조적 방법

- 구조적 방법 structural method

-> 기본 요소텍셀을 추출후 텍셀의 공간적 배열 탐색

- ex. 꽃밭 영상의 경우 -> 꽃이 텍셀

- 텍스처를 추출 할 대상은 지역적일수도 전역적일수도 있음 -> 어렵게 만듬

전역 기술자

1. 영상의 에지를 텍스처 기술자로 사용

2. 명암 히스토그램을  사용

=> 문제: 지역적 변화는 반영 불가

지역 관계 기술자

- 픽셀 간 관계 정의 및 표현 방법 필요

-> 동시 발생 행렬, 지역 이진 패턴

동시 발생 행렬 coocurrence matrix

- 명암 픽셀 쌍들을 조사하여 이웃간의 관계 정의 필요.

- 동시 발생행렬에서 행은 픽셀 쌍의 명암값, 열은 발생 횟수 표현

-> 명암 영상은 길이가 256이므로 256 x 256 크기로 동시 발생 행렬이 만들어짐.

지역이진패턴

- 지역적인 영역의 이진 패턴으로 텍스처 기술

- 종류

LBP Local Binary Pattern

LTP Local Ternary Pattern

LBP 지역 이진 패턴

- 텍스처 분류를 위한 특징이나 얼굴 인식 등에서도 많이 활용

- 모든 픽셀에 대해 계산. 중심 픽셀 주위의 밝기 변화를 이진화한 패턴

LBP와 얼굴인식 예시

- 얼굴 영역을 일정 크기 셀로 분할

- 각 셀별 LBP 히스토그램(LBP 인덱스 값에 대한) 계산

- 히스토그램들을 직렬로 연결한 벡터를 최종 특징으로 사용

 => 일종의 탬플릿 매칭

 * 셀 단위로 기하학적 정보 유지, 셀 내에선 텍스처 정보만 추출

LBP의 단점

- 명암이 균일한 부근에서 불안정

-> 명암들이 비슷한 부분에서는 어떻게 0과 1로 이진화 시킬까?

LTP Local Ternary Pattern

- 매개변수 t를 설정

- 중간 픽셀 화소에서 +- t 범위 안이면 0. +t보다 크면 1, -t보다 작으면 -1

- LTP 생성 : 2개의 LBP 생성됨 -> 512차원

=> 0, -1 -> 0, 1 -> 1으로 히스토그램 생성. LBP 1개

=> 1, 0 -> 0, -1 -> 1으로 히스토그램 생성. LBP 1개

PCA-SIFT

- 주요 방향 dorminant direction을 구하는 과정은 SIFT와 동일

- 특징 벡터 x 추출 과정이 다름

1) 키포인트 중심으로 39 x 39 윈도우 씌움

2) 윈도우 안 픽셀에 대해 y방향 x방향 도함수 영상 계산

3) 39 x 39 = 3,042 차원 벡터 획득 -> 너무크다

4) PCA Principal Component Analysis 주성분 분석으로 차원 축소하여 특징벡터 x로 취급

=> 4 * 4 * 8 = 128차원인 SIFT 기술자보다 PCA-SIFT는 차원 수를 크게 줄일수 있음

GLOH

- Gradient Location Orientation Histogram

- 원형 마스크(필터, 윈도우) 사용

- 원은 3등분, 두 바깥원들은 각각 8등분

- 분할된 영역들(16 + 1= 17개)에서 16단계 그라디언트 방향 히스토그램 계산

=> 17 x 16 = 272 차원 특징 벡터

- PCA 수행하여 272 -> 128차원 특징벡터로 취급 

이진 기술자

- 이전에 살펴본 특징 기술자들은 개당 128차원의 특징 벡터로 영상 처리하기엔 너무 큼

- 특징점 주위 두 픽셀을 비교쌍으로 사용. 픽셀들을 조사 후 수백개의 쌍으로 이진 배열 생성

- ex: BRIEF, ORB, BRISK

- 이진 기술자 조서 패턴 : 특징점 주위의 비교쌍들의 한쪽은 1, 한쪽은 0의 값을 가짐

이진 기술자들의 특징

- BRIEF : 가우시안을 따르는 두 점 조사 -> 스케일/회전에 영향 받음. 256개의 비교쌍 -> 256비트

- ORB : 회전 불변, 512 비트

- BRISK : 60개 점 설정 및 거리 조건 만족하는 쌍만을 비교쌍으로 사용. 회전 + 스케일 불변, 512 비트

이진 기술자와 일반 기술자 비교

- BRISK : 512비트

- SIFT 기술자 : 특징점 주위를 4등분. 한 영역에 4 x 4 x 8 = 128바이트. 128 x 4 = 512바이트

- BRISK의 크기 = SIFT 기술자의 크기/8

기술자 descriptor

- 특징점 내부와 주위로 부터 얻은 정보와 정보 추출 알고리즘

 => 특징에 대해 설명해줌

- 특징 벡터 feature vector : 일정 크기의 벡터임

특징 벡터와 기술자

- 패턴 인식에서 특징 벡터, 영상 처리에서 특징의 정보를 기술자라고 주로 부름

- SIFT, SURF와 같이 개선된 특징점 검출 알고리즘을 구했다면, 기술자도 좋은 기술자를 구해야함.

특징 기술자 성질

- 기술자끼리 구분 가능해야함 -> 이후 매칭시 대응하기 위함

- 불변성 : 영상이 회전, 크기, 광도 등 변환이 일어나도 기술자는 불변해야함

- 특징 벡터의 크기를 줄여야 함 -> 한 영상에서 특징 수천개 존재, 매칭시 특징간 거리 계산하므로 차원이 낮아야함.

관심점의 정보

- 스케일 정보가 없는 경우 (y, x)

- 스케일 정보를 갖는 경우 (y, x, omega)

SIFT 특징

- 키포인트라고도 부름

- 스케일 정보를 가진 (y, x, omega) 형태 -> 스케일 변환에 불변

- 회전 변환에 불변하기 위한 정보가 필요

주요 방향의 필요성

- 회전 불변하기 위한 정보가 필요 -> 주요 방향 dominant orientation을 우선 찾음

 1) 키포인트 중심으로 윈도우(커널)

 2) 윈도우 내 픽셀에 대해 그라디언트 방향 히스토그램으로 주요 방향 찾음

  * 10도 간격으로 양자화 -> 히스토그램은 36칸 가짐

  * 그라디언트 크기에 가우시안을 컨볼루션하여 멀수록 작은 가중치 반영

  => 히스토그램에서 가장 큰 값을 나타내는 방향이 주요 방향

- 아래의 그림은 이미지 그라디언트와 키포인트 기술자 예시

 * 좌측은 방향이 10도 간격으로 양자화(36단계)됨, 우측은 8단계로 양자화된 그라디언트 방향 히스토그램

키포인트 정보

- (y, x, omega, theta)로 정리.

- 기술자를 얻기 위해 윈도우 컨볼루션

 * 주요 방향이 기준이 되도록 좌표계 설정 -> 방향 불변성 성립

1) 위 그림에서 한박스만 보자. 윈도우를 4x4로 분할하여 블록이 16개 존재. 현재 10도 간격으로 36단계의 방향이 표현됨

2) 위 블록에 존재하는 16픽셀의 그라디언트를 계산하여, 8단계 양자화된 그라디언트 방향 히스토그램 추출

=> 이 데이터는 4(가로박스 개수)x4(새로박스 개수)x8(방향) = 128차원의 특징 벡터 x가 됨

3) 벡터 x를 벡터의 크기 ||x||로 나누어 단위 벡터 획득

 => 회전, 광도 불변한 128차원 SIFT 특징 기술자 완성

SIFT 기술자 추출기

- 입력 : SIFT detector로 검출한 특징점(관심점, 키포인트 - y, x, omega)

- 출력 : 키포인트(기존의 키포인트 + 주요 방향 + 특징벡터 x)

민시프트

- 클러스터링 알고리즘 중 하나

- 파젠창 방식 : 각점에 대한 샘플의 확률들을 구함

- 초기점을 지정하고, 커널 안에서 같은 분류에 속하는 점들의 방향으로 따라감

- 장점

 1) kmeans 같은 군집화 알고리즘과 달리 군집 개수를 알 필요 없음. 자동으로 군집 개수 찾음

 2) kmeans 같은 알고리즘은 일정 형태의 분포를 가정하여 변수들을 추정하는 모수적 방법

  <-> 민시프트는 임의의 분포에서 찾음. 비모수적 방법

 3) 필요한 파라미터가 커널의 폭 h뿐임

=> 얼굴 추적, 영상 검색 등 많이 활용

다른 대표적인 군집화 알고리즘

- kmeans

- DBSCAN

kmenas

- 유명한 군집화 알고리즘 중 하나

1) 군집 개수를 지정

2) 군집 개수만큼 임의의 중심점들을 생성

3) 중심점과 점들 사이의 거리로 점들의 소속 중심점 분류

4) 소속 중심점들의 평균 위치로 중심점을 이동

5) 반복하면 처음 지정한 군집개수만큼 분류 완료

- 장점 : 빠름

- 단점 : 군집 개수 지정해야함, 임의의 중심점으로 초기화하므로 매번 결과가 다를수 있음

DBSCAN Density Based Spatial Clustering of Application with Noise

1) 임의의 시작점에서 시작

2) 거리 엡실론에 속하는 이웃들을 추출.

3) 이 이웃들이 충분히 있으면 클러스터링 수행. (노이즈 샘플이라) 충분히 존재하지 않는 부분에는 클러스터링 x

4) 반복하면 하나의 클러스터가 완료

5) 다른 방문하지 않은 점들에 대해 클러스터링을 다시 수행

- 장점 : 군집 개수 지정 필요 없음. 민시프트에서 점들이 다르면 다른 군집으로 판단했으나, 아웃라이어를 노이즈로 판단해서 포함시킴

- 단점 : 동작이 힘듬

https://michigusa-nlp.tistory.com/27

민시프트를 이용한 영상 분할 예시