목표
- 캐닝 에지 컨샙 배우기
- cv2.Canny()함수 배우기
이론
- 캐니 에지 검출기는 많이 사용하는 에지 검출 알고리즘으로 196년 존 F 캐니가 만들었습니다. 이 캐니 에지 알고리즘은 여러 단계로 구성된 알고리즘으로 다음과 같습니다.
1. 노이즈 제거
- 에지 검출기는 어느정도 노이즈에 강인해야 하기때문에 첫 단계에서는 5 x 5크기의 가우시안 필터로 노이즈를 제거합니다. 이에 대해서 이전에 봤으니 넘어가겠습니다.
2. 이미지의 그라디언트 강도 계산하기
- 노이즈가 제거된 이미지는 그 다음에 소벨 커널로 수평과 수직 방향으로 필터를 적용하고 수평 방향에 대한 1차 미분 영상과 수직 방향에 대한 1차 미분 영상을 얻습니다.
- 이 두 영상을 가지고 에지 그라디언트와 방향을 얻을수 있게 됩니다
- 그라디언트 방향은 항상 에지에 수직이며, 수직, 수평 그리고 두 대각 방향 중 하나를 의미하는 값이라 할수 있겠습니다.
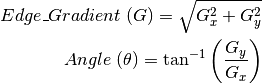
3. 비최대 억제 - non-maximum suppression
그라디언트의 크기와 방향에 대한 정보를 얻으면 이제, 에지가 아닌 픽셀들을 제거하여야 합니다.
- 이 때, 모든 픽셀들은 그라디언트의 방향에 존재하는 이웃 점들과 비교하여 지역 최대점인지 확인하여야 합니다.
- 아래의 그림에서 A는 에지로(수직 방향에 대한), 그라디언트 방향은 에지와 돌일 합니다.
- B,C는 그라디언트 방향에 존재하는데, 점 B, C가 지역 최대점인지 확인여야 하고 아닌 경우들은 0으로 놓습니다.

4. 가정 임계화 hysteresis Thresholding
- 이번 단계에서는 모든 에지가 실제 에지인지 아닌지 판단하여야 합니다. 여기서는 최소, 최대를 나타내는 임계값을 사용하겠습니다. 어느 에지가 maxVal보다 크면 에지, minVal보다 작으면 에지가 아니므로 버립니다.
- 이 두 임계치 사이에는 연결성을 이용해서 에지 여부를 판단하는데요. 사이에 존재하는 픽셀들이 확실히 에지인 것과 연결되어있다면 에지의 일부분으로 판단하고, 연결되지 않았다면 버리게 됩니다.

- 위 그림의 경우 에지 A는 최대값을 넘어가므로 확실한 에지가 됩니다. 에지 C의 경우에는 최대 값보다 밑에있으나 A에 연결되어 있으므로 이 또한 에지라고 판단합니다.
- 하지만 에지 B의 경우 최소값은 넘어가지만 확실히 에지인것과 연결되어있지 않으므로 버립니다. 그래서 최대 최소 임계치를 잘 결정해야 올바른 결과를 얻을수가 있겠습니다.
케니 에지 검출기
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread("C:/Users/do/Documents/github/opencv_python/res/kimheungkook.jpg",0)
edges = cv2.Canny(img,100,200)
plt.subplot(121),plt.imshow(img,cmap = 'gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])
plt.show()

'로봇 > 영상' 카테고리의 다른 글
| opencv-python 튜토리얼 - 15. 히스토그램 (0) | 2020.08.15 |
|---|---|
| opencv-python 튜토리얼 - 14. 이미지 피라미드 (0) | 2020.08.15 |
| opencv-python 튜토리얼 - 12. 이미지 그라디언트 (0) | 2020.08.14 |
| opencv-python 튜토리얼 - 11. 모폴로지 연산 (0) | 2020.08.14 |
| opencv-python 튜토리얼 - 10. 이미지 스무딩 (0) | 2020.08.14 |