Bode 선도
- 주파수 응답을 로그스케일의 주파수에 대해 크기는 데스벨, 위상은 각도로 직교좌표계상에 나타낸것
- 주파수 응답을 표현하는 가장 일반적인 방법
=> 시스템 주파수 응답을 쉽게 이해할 수 있음
Bode 선도
- 주파수 omega에 따른 주파수 전달함수 크기 M(omega)와 위상 phi(omega)를 직교 좌표계상에 나타낸 선도
- 주파수 omega : 수평축에 로그 스케일로 표시
- 크기 M(w)와 위상 phi(omega) : 수직 축에 데시벨과 각도로 표시
M dB = 20 log|G(jw)|
- Bode 선도가 주파수 응답 특성을 나타내는 선도 중 가장 보편적으로 사용됨
(시스템 모델링, 해석 및 설계 시 모두 사용)
Bode 선도의 장점
1. 주파수 전달함수를 여러개 기본 요소로 분리 가능하므로 주파수 응답을 조직적이며 쉽게 구할 수 있음
-> 크기 : |G(jw)| = log|G1 G2 Gn| = log|G1| + ... + log|Gn|
-> 위상 : <G(jw) = <(G1 G2 .. Gn) = <G1 + <G2 + ... + <Gn
2. 점근선을 이용하여 복잡한 주파수 전달함수를 쉽게 선도화 함
3. 로그 스케일로 주파수를 표시하여 넓은 주파수역 표시 가능
-> 중요한 저주파역은 확대하고 상대적으로 덜중요한 고주파역은 축소한 합리적인 표현임
4. 실험적으로 구한 Bode 선도로부터 전달함수 유도가 가능함
5. 제어기 설계 시, 제어기 첨가와 제어기 파라미터 효과를 쉽게 파악할수 있음
전달함수 G(s)의 4가지 기본요소의 Bode
1. 상수 게인 요소 : G(s)=K
2. 미분 or 적분 요소 : G(s)=s or G(s)=1/s
3. 실수축상에 있는 극점 or 영점 요소 ; G(s)=1/(1+Ts) or G(s)=1+Ts
4. 복소 극점 or 영점 요소
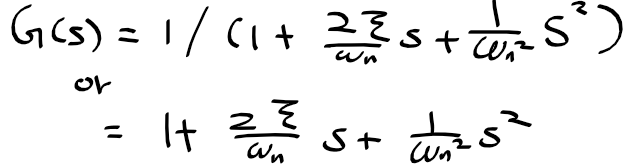
1. 상수 게인 요소, G(s)=K의 보드 선도


2. 미분 적분 요소, G(s)=s , G(s)=1/s의 보드선도
1) 미분 요소 G(s)=s에 대한 크기 M(omega)와 위상 phi(omega)


2) 적분 요소 G(s)=1/s에 대한 크기 M(omega)와 위상 phi(omega)

3. 실수 축상에 극점 또는 영점 요소의 bode 선도
1) 실수 축상에 있는 극점 요소의 주파수 전달함수와 크기, 위상

주파수 전달함수의 크기 M(w)와 위상(w)의 근사값

- 저주파 영역에서 크기는 0, 위상 0
- 고주파 영역에서 크기는 20 log wT, 위상 -90

4. 복소 극점 또는 영점 요소의 Bode 선도
- 실수축상에 있는 극점 요소의 주파수 전달함수
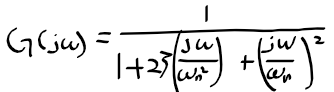
- 복소 극점 요소의 크기 M(w)와 위상 phi(w)



주파수 응답에 대한 사양
1. DC 게인 M_0
- 주파수 omega=0일때 시스템 게인
2. 대역폭 w_b
- 주파수 전달함수 크기가 20log M_0 -3 dB일때의 주파수
입력에 대해서 출력이 w_b만큼 쫒아갈 수 있음.
3. 공진 최댓값 M_r
- 시스템 주파수 응답 중 시스템 게인 최댓값
4. 공진 주파수 w_r
- 공진 최댓값이 나타나는 주파수
5. 차단률 cutoff rate
- 고주파역에서 게인이 떨어지는 or 롤오프(roll-off)하는 정도. 차단율이 클수록 고주파 성분이 빨이 줄어듬
=> 시스템 입력신호에서 잡음(주로 고주파)을 차단하는 특성을 나타냄

단순 2차 시스템의 전달함수에 대한 주파수 응답 사양
- 공진 주파수

- 공진 최댓값
공진 최댓값 M_r은 감쇠비 zeta에 의해서만 결정
- 대역폭 w_b

질량-스프링-댐퍼 시스템의 주파수 응답
F(t)를 입력, x(t)를 출력으로하는 전달함수 G(s)

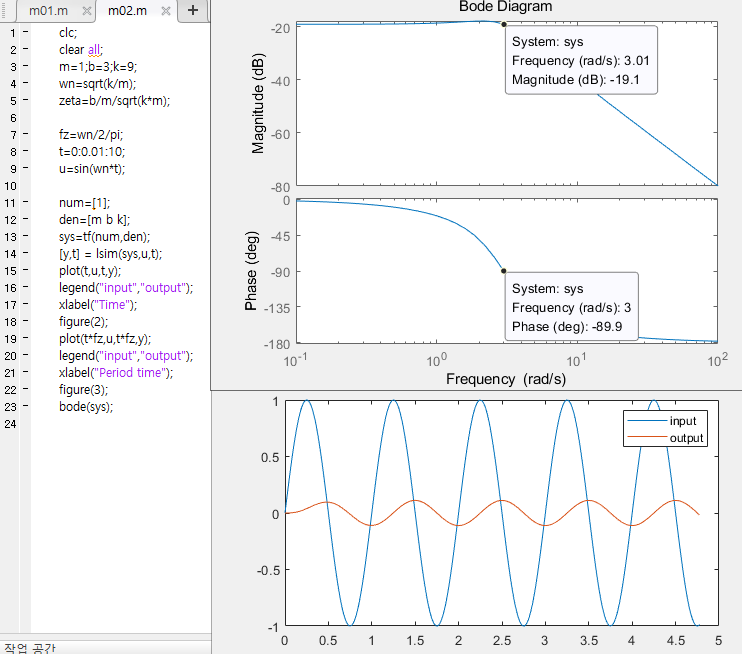
G(s)의 보드선도
- m=1, k=9, b=3, zeta=0.5, wn=3(rad/s)

전달함수 G(s)의 Bode를 구하는 매트랩 코드

주파수 입력 F(t)=sin(wn t)에 대한 과도응답과 Bode 선도 비교
- 고유진동수 wn=3 일때 위상차 -90이며 크기는 -19 dB
-> 과도응답 출력 위상이 입력의 -90도이며 출력의 크기도 입력보다 작음
질량 스프링 댐퍼 시스템의 주파수 응답
m=1, k=9, b= 1 ~11까지 변하는 동안 G(s)의 Bode 선도를 구해보자
- 저주파나 고주파에서는 b의 변화에 따라 비슷한 특성을 보이나 wn=3 부근에서 특성이 달리 보임

'로봇 > 제어' 카테고리의 다른 글
| 제어공학 2 - 21 주파수 응답을 이용한 안정도 판별 (0) | 2020.05.11 |
|---|---|
| 제어공학 2 - 20 Nyquist 선도 (0) | 2020.05.11 |
| 제어공학 2 - 18 주파수 응답 (0) | 2020.05.10 |
| 제어공학 2 - 17. 근궤적법을 이용한 뒤짐보상기 설계 (0) | 2020.05.10 |
| 제어공학 2 - 16 근궤적법을 이용한 앞섬 보상기 설계 (0) | 2020.05.10 |