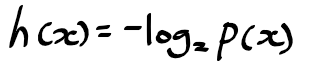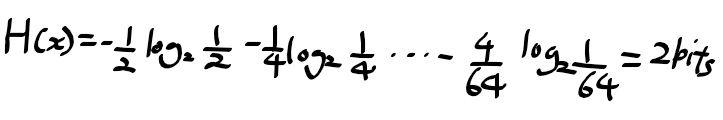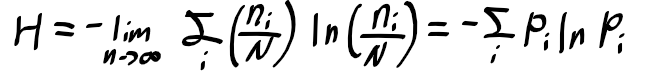집밖은 위험해

이미지의 해상도 조절

- 업샘플링 : 해상도를 늘리는 영상 처리

- 다운 샘플링 : 해상도를 줄이는 영상 처리

- 이미지 피라미드 : 업샘플링/다운샘플링 연산을 통해 획득한 다중 해상도 영상

* 이미지 피라미드 예시

영상 처리의 기본 영상

- 점 연산 : 자기 값만 보고 새 값을 결정

- 영역 연산 aera operation : 이웃화소들을 보고 값을 결정

- 기하 연산 geometric operation : 기하학적 규칙에 따라 다른 값을 취하는 방법

점 연산

- 점연산의 대표적인 예시로 이진화

 -> 해당 픽셀이 임계치를 넘으면 1, 아니면 0

영역 연산

- 상관(필터)과 컨볼루션이 있음

상관 연산 filtering

- 1차원의 경우 : 윈도우(커널)을 입력 영상의 첫번째부터 끝까지 밀면서 연산

- 2차원의 경우 : 원도우(커널)을 0,0 좌표에서 일정 간격(스트라이드)밀면서 다음 행으로 넘어가도록 반복

컨볼루션 convolution

- 1차원의 경우: 상관 연산과 동일하나 윈도우(커널)을 뒤집어서 수행

- 2차원의 경우 : 상관 연산과 동일하나 윈도우(커널)을 뒤집어서 수행

상관 연산과 컨볼루션 구분 이유

- 물체 검출 용도의 경우 상관 연산 사용

- 신호 처리시 임펄스 응답을 얻기 위해 컨벌루션 연산 사용.

* 아래는 시불변 시스템에 임펄스 신호를 컨벌루션하여 임펄스 응답을 구하는 과정을 나타냄

커널(마스크, 윈도우)의 역활

- 정규 마스크 normalized mask : 마스크의 화소가 합하면 1이되는 마스크로 화소 평균을 구함.

- 가우시안 마스크 : 잡음 제거하며, 스무딩이라고도 부름

- 샤프닝 마스크 : 에지를 강조하는 역활 수행

- 에지 마스크 : 미분 연산자로, x방향, y방향 에지들을 강조하는 역활

* 아래는 가우시안 마스크와 가우시안 블러링 결과

* 에지 검출 용 마스크. 소벨 에지 마스크

비선형 연산

- 컨볼루션은 입력 이미지와 뒤집힌 커널의 선형 결합을 구하는 선형 연산

- 비선형 규칙을 적용하면 비선형 연산

메디안 필터

- 대표적인 비선형 연산 중 하나로 

기하 변환 geometry transformation

- 동차 좌표계에 동차 행렬을 곱하여

  이미지의 이동, 회전, 크기 기울기 변환 등을 수행하는 변환

- 강체 변환 rigid transform(유클리디안 변환) : 이동 + 회전

- 유사 변환 similarity transform : 크기 변환

- 어파인 변환 affine transform : 강체 변환 + 스케일링 + 기울기 

- 원근 변환 perspective transform : 어파인 변환 + 투영

ref : darkpgmr.tistory.com/79

이미지의 화소 pixel은 일반 적으로

사각형의 형태를 이용한다.

이진 영상의 예시

서로 만나는 화소의 관계로

4-연결성 4connectivity와 8-연결성 8-connectivity가 있음.

이번에는 확률 분포와 이들의 속성을 살펴볼건데

이 확률 분포들은 다양한 모델들을 만드는데 사용된다.

이번에는 베이지안 추론 같은 핵심 통계wjr 개념들을 살펴보고,

차후에 간단한 모델을 만들어보자.

N개의 유한개의 관측 집합으로 확률 변수 x에 대한 확률 분포를 구할건데

이 문제를 밀도 추정 density estimation이라 부른다.

이 문제를 다루기 위해서 모든 점 데이터들은 독립적이며 동일한 분포를 따른다고 가정할 것이며,

관측 된 데이터셋으로 너무 많은 확률 분포들을 구할수 있기 때문에 이런 밀도 추정의 근본적인 한계도 볼것이다.

그래서 이전에 다항 커브 피팅 시 적절한 분포를 선택하는 문제를 다뤄봤으며, 패턴 인식의 핵심 문제이기도 하다.

모수적 밀도추정 parametric density estimation

이산 확률 변수를 다루는 이항 분포와 다항 분포를 다뤄볼것이고, 연속 확률 변수에 대한 가우시안 분포를 살펴볼것이다.

이들은 평균과 분산같은 몇가지의 수로 주요 성질들을 나타낼수 있어

모수 분포 parametric distribution이라고도 부른다.

이 모델들로 밀도 추정에 사용하기 위해선, 주어진 데이터로부터 적절한 모수 값들을 찾아내어야 하는데

빈도주의자들은 가능도 함수 같은 몇가지 기준들을 최적화하는 방식으로 모수들을 찾아낸다.

베이지안의 경우에는 모수에 대한 사전 확률을 구하고,

베이즈 정리를 통해 관측 데이터가 주어지면 이로부터 사후확률을 계산한다.

여기서 켤레 사전 분포가 얼마나 중요한 역활을 하는지 보게 될건데 베이지안 분석을 간소화 시키게 한다.

* 켤레 분포 conjugate distribution : 베이즈 정리의 사전, 사후확률을 켤레 분포라 부름

* 켤레 사전 확률분포 conjugate prior : 결레 분포중 사전 확률 분포

* ref : en.wikipedia.org/wiki/Conjugate_prior

다항 분포의 모수에 대한 켤레 사전 확률 분포는 dirichlet 분포라 부르고,

가우시안 분포의 평균에 대한 켤레 사전 확률 분포는 다른 가우시안 분포가 된다.

이러한 모든 분포들을 확률 분포의 지수족이라 하며, 매우 중요한 속성들을 가지고 있으므로 자세히 살펴보아야한다.

비모수적 밀도추정 nonparametric density estimation

모수적 방법의 한계로는 특정한 확률 분포를 따른다는 점인데, 특정 상황에서는 부적절할 때가 있다.

그래서 이를 대신하는 방법으로 비모수적 밀도 추정 방법이 있는데,

이는 데이터 셋의 크기에 의존하는 확률 분포의 형태를 띄며

이 모델역시 모수를 가지고 있지만, 분포의 형태 보다는 모델의 복잡도를 제어한다.

마지막으로 세가지 비모수적 방법인 히스토그램과 최근접이웃, 커널 방법들을 살펴보겠다.

정보 이론 information theory

그동안 패턴 인식에 기반이 되는 확률 이론과 결정 이론에 대한 개념들을 살펴봤고,

이번에는 정보 이론에 대해서 알아보자

이산 확률 변수 x가 주어졌을때 이 확률 변수에는 정보가 얼마나 있는지 궁금할수 있다.

정보의 양은 x를 학습하는 중에 발생하는 놀람의 정도(degree of surpise, 갑작스러운 변화의 정도)로 볼수 있는데

예상치 못한 상황이 많이 발생할수록 그렇지 않은 경우보다 정보가 많다고 할수 있으며

혹은 특정한 상황이 발생하지 않는다면 정보가 없는게 된다.

정보의 양

그래서 정보의 양에 대한 척도는 확률 분포 p(x)에 영향을 받으며

정보의 양을 나타내는 h(x)는 확률 변수 p(x)가 얼마나 단조로운지, 변화가 없는지에 대한 함수라고 할수있겠다.

두 사건 x, y가 전혀 상관관계가 없는 경우 이들로부터 얻을수 있는 정보의 양은

각 정보의 양의 합이되며 h(x, y) = h(x) + h(y)가 된다.

두 사건 x, y는 독립이므로 p(x, y) = p(x) p(y)도 되겠다.

h(x)를 구하는 간단한 방법으로 확률 분포 p(x)에 로그를 취하면 되는데

아래와 같이 음의 부호를 붙임으로서 정보의 양이 양의 값이나 음의 값을 가지게 된다.

* p(x)는 0 ~ 1사이 값을 가지므로, 로그를 취할 시 음수가 되기 때문

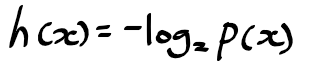
엔트로피 entropy

엔트로피 = 정보의 양에 대한 기대값(정보의 불순 정도)

위 식을 보면 사건 x가 발생할 확률이 적을수록 정보의 양이 크다는 점을 알수 있는데, 

h(x)의 단위는 비트 단위이므로, 로그의 밑이 2인 로그를 사용한다.

한번 송신자가 수신자에게 확률 변수 값들을 보내는 경우를 생각해보자.

여기서 보내지는 정보의 평균 양은 확률 분포 p(x)에 대한 위 식의 기대값으로 구할수 있는데 아래와 같다.

이 양을 확률변수 x에 대한 엔트로피라 부른다.

엔트로피와 불순도

지금까지 정보의 정의와 엔트로피에 대해서 살펴보았고, 이 개념이 얼마나 유용한지 알아보자

경우 (1)

확률 변수 x가 8가지 경우가 존재하고, 각각 경우의 확률들은 동일하다고 생각해보자.

* p(x = x1) = 1/8, p(x = x2) = 1/8, ...

x의 값으로 수신자에게 정보를 보낸다고 한다면, 길이가 3비트인 메시지를 전송하면 되겠다.

이 확률 변수의 엔트로피는 아래와 같이 구할수 있다.

하지만 위 경우는 모든 경우의 수가 동일한 확률일 경우를 가정한 경우이고

경우 (2)

8가지 상태 {a, b, c, d, e, f, g, h}가 있을때 각각의 상태의 확률이 {1/2, 1/4, 1/8, 1/16, 1/64, 1/64, 1/64, 1/64}라고 할때

엔트로피는 아래와 같이 구할수 있다.

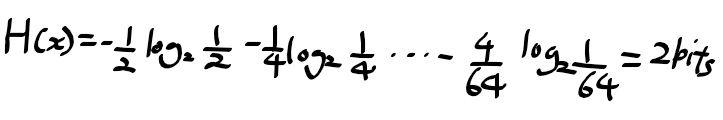
위의 두가지 경우 균일하지 않은 분포일수록 균일한 경우보다 엔트로피 값이 작아진다는것을 알 수 있는데,

이를통해 엔트로피라는 용어가 불순도의 정보를 의미한다는 것을 알수있다.

다시보면

경우 1은 aaabbbcccdddeeefffggg..... 모든 상태가 균일하므로 불순도가 크므로 엔트로피가 크지만

경우 2는 aaaaaaaaaaaaaaaaaabbbbbbbccccddefg같이 불균일하게 되면서 경우 1보다 불순도가 떨어져 엔트로피가 작다

엔트로피로 보는 코드 스트링 해독

상태 값들을 보내는 경우를 생각해보자 8가지의 경우가 존재하므로 3비트 수를 사용하면 좋을것 같지만,

경우 2는 비균일 분포를 따르고 있으므로 많이 발생하는 경우 짧은 코드를 사용하도록하면

전체 코드 길이를 줄일수 있는 장점이 생기게 된다.

{a, b, c, d, e, f, g, h}를

0, 10, 110, 1110, 111100, 111101, 111110, 111111라는 코드 스트링으로 나타내자

통신을통해 보내지는 코드의 평균 길이는

확률 변수의 엔트로피와 동일한 값을 가지게 된다.

여기서 주의해야하는건 이보다 짧은 코드 스트링을 사용해선 안되는데,

연결된 문자열을 부분 부분으로 나눌때, 차이를 구분해야하기 때문이다.

11001110의 경우 110, 0, 1110으로 나누어서 보면 cad로 해독할수 있겠다.

엔트로피와 최단 코드 길이는 동일한 것으로 볼수 있는데,

노이즈리스 코딩 이론에 따르면 엔트로피는 확률 변수 상태들을 전송하는데 필요한 비트 수의 하한이라 할수있다.

다중성 multiplicity와 엔트로피

지금까지 정보의 평균 양으로서 엔트로피를 살펴봤는데,

엔트로피라는 개념은 물리학의 평형 열역학에서 소개되었으며, 이후 통계 분야의 불순도 척도로서 사용되었다.

이제 엔트로피를 몇개의 구간으로 나눌수 있는 N개의 동일한 객체들로서 엔트로피를 살펴보자

객체들을 일정 구간으로 나누는 방법의 수를 생각해보자,

첫번째 물체를 선택할때 N가지의 경우, 두번째 물체의 경우 (N - 1)의 경우

천체 N개의 물체들을 구간화하기위한 전체 경우의 수는 N!가 되겠다.

하지만 물체들을 각 구간별로 구분시키고 싶지 않다면,  i번째 구간에 n_i!가지의 정렬하는 경우가 있다고 치고

전체 N개의 물체를 구간별로 배정하는 방법의 수는 아래와 같이 구할수 있으며

이를 다중성 multiplicity라 부른다.

엔트로피는 적절한 상수로 조정된 다중성의 로그로 정의된다.

여기서 N이 무한대로 된다면 n_i/N은 특정 값으로 수렴이되고, Stirling의 근사를 적용하면

아래의 엔트로피에 관한 식을 얻게 된다.

이로부터 상태 x_i를 이산 확률 변수 X의 구간으로 볼수 있으며, p(X = x_i) = p_i가 되고

확률 변수 X의 엔트로피는 아래와 같이 정의가 되겠다.

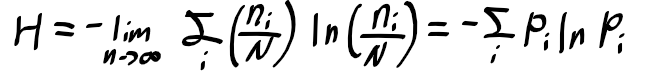
뾰족하게 생긴 p(x_i)에 대한 분포는 작은 엔트로피(불순도가 작음=타 경우의 확률이 적음)값을 가지며,

반대로 높은 엔트로피의 값을 가지는 경우(불순도가 큼=타 경우가 자주발생) 확률 변수의 분포는 균일한 형태를 가지게 된다.

결정 이론 개요

지난번에

확률 이론이 불확실성을 수치화 해서 다루는 수학적 기반으로 사용된다고 알아봤고

이번에는 확률 이론에 기반한 결정 이론에 대하여 살펴보겠다.

결정 이론은 주어진 불확실한 상황에서 어떻게 최적의 결정을 할수 있게 만드는지에 대한 학문이라 할수있다.

입력 벡터 x와 타겟 벡터 t가 주어지고, 우리는 새로운 x가 입력될때 t를 예측해야한다고 하자

회귀 문제에서 t는 연속 변수이고, 분류 문제에서 타겟벡터 t는 클래스의 카테고리, 라벨같은것을 의미한다.

결합 확률 분포 p(x, t)는 이러한 변수들 사이 불확실성을 완전히 정리해주는데

훈련 데이터 셋으로 구한 결합 확률 분포 p(x, t)의 결정식을 구하는 것이

확률적 추론이며, 앞으로 다루고자 하는 내용이라 할수 있다.

여기서 중요한점은 t를 예측하는 과정이 너무 과적합이 아닌 일반화 될수있어야 하는데

이게 결정 이론의 핵심이라 할수 있겠다.

의학 진단으로 보는 결정 이론 : 환자의 X ray 영상으로 이 환자가 암이 있는가 없는가? 판단하기

결정 이론을 다루는 예시로

환자의 Xray 영상이 있는데, 이 영상으로 환자가 암인지 아닌지 판단하여야 한다.

이때 입력 벡터 X는 이미지 픽셀들로 이루어지고

t는 암의 존재여부 그러니까 이진 클래스로 주어지겠다.(암이면 1, 암이 아니면 0인 식으로)

앞으로 라벨 값을 선택하는데 확률 모델이 어떻게 유용한지 알아보겠다.

일반적인 추론 문제에서는 결합 확률 분포 p(x, t)를  다루게 되는데

주어진 상황을 고려하여 최적의 선택을 하는, 환자 여부를 선택하는 것이 결정이며

결정 이론은 주어진 확률들에 기반하여 얼마나 최적의 결정을 했는지를 알려준다.

아무튼 우리가 해야할 건 이미지 x가 주어졌을때 클래스에 대한 확률(사후확률)을 구하여야 한다.

이를 베이즈 정로로 표현 하면 다음과 같다.

여기서 우리가 해야할 일은 

x ray 정보가 주어졌을때 오분류 하는 경우를 최소화 시켜야 한다.

오분류 최소화 하기

아무튼 우리가 해여할 일은 x가 주어졌을 때 가능한 클래스 들중 하나를 선택하는 결정규칙 decision rule이 필요하다.

결정 규칙은 입력 공간을 결정 영역 R_k로 분할시키는데, 각 결정영역에는 클래스 C_k가 주어진다.

결정 영역 decision region 사이의 경계를 결정 경계 decision boundary, 결정 표면 decision surface라 부른다.

최적의 결정 규칙을 찾기위해 암 여부 판단 문제로 한번 보자

실수가 일어날 확률을 아래와 같이 정리할수 있다.

이제 우리가 할일은 오류 확률을 최소화 하는 결정 규칙을 구하면 되는데

실수를 최소화 시킨다는 말은

올바르게 분류하는 사후확률을 구한다는 말이기도 하다.

K개 클래스로 일반화 해서 본다면 x가 주어질때, 각각의 p(x, C_k)가 가장 커지는 결정 영역을 구하면 된다.

P(x, C_k)는 확률의 곱 법칙에 따라 x가 주어질때 C_k에 대한 사후확률과 p(x)로 분해할수 있고

결국에는 가장 큰 사후확률을 찾는 문재가 된다.

암을 판별하는 이진 분류 문제를 그림으로 표현하면

정분류율읠  최대화 하는 결정 경계는 아래와 같이 x0라 할수 있다.

기대 손실 최소화하기

실제로 사용하기 위해선, 오분류율을 줄이는 단순한 문제보다 복잡한 문제들을 다루어야 한다.

다시 암 진단 문제를 다시 생각해보자

암이 없는 환자를 암이 있다고 오판하는 경우(1)보다

암이 있는데 없다고 판단하는 경우(2)가 위험이 매우 크다.

(1)에 의한 손실보다는 (2)에 의한 손실을 줄이는게 더 나으므로

이를 수식화 하기 위한 개념으로 손실 함수 loss function, 비용함수 cost function가 있으며

이 손실 함수는 결정에 따른 손실, 손해의 척도로 사용된다.

입력 x가 주어졌을때, 실제 클래스가 C_k이지만 C_j로 잘못 분류한 경우가 있다 하고,

이때 손실을 L_kj라고 표기하고 여기서 k와 j는 나중에 나올 손실 행렬의 원소로 보자.

아래의 그림은 암 판별 문제의 손실 행렬을 보여주고 있는데,

건강한 사람이 암으로 판단된경우 손실은 1이고, 반대로 암 환자가 정상으로 판별한 경우 손실은 1000이다.

최적해 optimal solution은 손실 함수를 최소화 시켜서 구할수 있지만

손실 함수는 우리가 실제로는 알수 없는 진짜 클래스에 의존하는게 문제다.

입력 벡터 x가 주어질때 실제 클래스에 대한 불확실성은 결합 확률 분포 p(x, C_k)로 나타낼수 있으니

이 분포에 대한 평균 손실을 최소화 하는 방향을 사용하여야 한다.

다시 정리하면, 기대 손실(위의 식)을 최소화하는 결정 영역 R_j들을 구하여야 한다.

적분항 내부 결합 확률 분포는 확률 곱의 법칙에 따라

아래와 같이 분해할수 있고,

p(x)는 제거하면

기대 손실을 최소화 하는 결정 규칙은 새 입력 x가 j에 속하는 경우 아래의 식과 같다.

암 판별 문제의 기대 손실은 정리해보면 아래와 같다.

손실 행렬에 의해 암인데 정상으로 판단되는 부분에 큰 가중치를 주고,

정상인데 암으로 판단하는 경우 적은 가중치를 줌으로서

암을 정상으로 판단하는 경우를 크게 줄일수 있는 방향으로 결정 영역을 찾게 된다.

회귀 문제와 비용함수

지금까지 분류 문제를 다루기 위해 결정 이론을 살펴보았고

이제 회귀 문제에 적용해보자

앞에서 입력 x가 주어질때 추정자 y(x)로 t를 추정해 왔었다

이를 비용 함수로 나타내면 L(t, y(x))가 되는데,

이를 기대 손실로 나타내면 아래와 같다.

회귀 문제에서 비용 함수는 일반적으로 손실의 제곱을 많이 사용하는데

그러면 기대 손실을 아래와 같이 고칠수 있겠다.

이제 할일은 기대 손실 E(L)을 최소화 하는 y(x)를 구하면 되겠다.

기대 손실 E(L)을 y(x)에 대해 편미분할수 있는데

확률의 하브 곱 법칙으로 y(x)에 대한 해를 구할수 있다.

이 식은 x가 주어질때 t의 기대값으로 회귀 함수라 한다.

지난번에 커브피팅하는 방법을 오차 최소화 함으로써 구해보았는데

이번에는 확률론적인 관점에서 보자

입력 벡터 x, 계수 벡터 w, 그리고 정밀도 파라미터 beta가 주어질때,

타겟 벡터 t에 대한 확률이 가우시안 분포를 따른다면 아래와 같이 정리할수 있다.

위 식에서 beta는 정밀도 계수인데

베타의 역수가 정규분포의 분산이 된다.

정밀도가 1에 가까우면 정규분포의 분산이 줄어들고

정밀도가 0에 가까우면 정규분포의 분산이 커지게 된다.

이제 훈련 데이터 x, t가 주어질떄 최대가능도법으로 다항 계수 벡터 w와 정밀도 베타를 구해보자

우선 가능도 함수를 정의하고,

이 가능도 함수를 음의 로그변환을 시켜주면 아래와 같다.

이전에 했던방법대로

훈련 데이터 x, t가 주어질때 오차를 최소화 하는 다항 계수 벡터와 베타를 구할수 있는데

베타 최대 가능도 추정량은 경우 다음과 같이 정리할수 있다.

이제 다항 계수 벡터 w와 정밀도 beta의 최대 가능도 추정량을 구하였으므로

새로운 데이터 x가 주어질때 다항 회귀 값인 t를 추정하는 확률 모델(가능도 함수)를 구할수 있는데

이 모델은 단순이 첨추정할뿐만이 아니라 확률 분포를 알려주는 예측 분포 predictive distribution라고 부르겠다.

베이지안 방법을 하기 위해서

다항 회귀 계수에 대한 사전 확률 분포를 정의하면 

아래와 같은데, 여기서 알파값은 이 분포의 정밀도로 직접 조절하는 값 하이퍼 파라미터라 부른다.

베이즈 정리를 이용해서 w에 대한 사후확률 분포는 

아래와 같이 가능도 확률 모델과 사전 확률 분포의 곱으로 정의하여 구하며,

학습 데이터 x, t와 하이퍼 파라미터 알파 베타가 주어졌을때

가장 가능성 있는 w에 대한 사후확률 분포를 구하는것을 사후확률 최대화 방법 MAP라 부른다.

x가 열린 구간 (a, b)에 속하는 경우에 대한 확률

확률 p(x)이 전체 구간에 대한 합

누적 확률 분포 함수 P(z)

두 확률 변수 x, y의 합. 베이즈 정리를 이용한

확률 분포 함수 p(x)를 따르는 일련의 함수 값 f가 주어질때 기대값

조건부 확률의 기대값

일련의 함수 f에 대한 확률 분포 

두 확률 변수와 두 벡터에 대한 공분산

베이즈 정리

관측 데이터 벡터 D와 확률 분포의 모수 W 사전 확률 분포 P(W)가 주어질때

아래의 관계를 가짐

사후 확률 = 가능도 x 사전 확률

빈도론적 관점과 베이지안적 관점

빈도론적 관점과 베이지안 관점에서 가능도 함수 p(D|w)는 매우 중요한데,

빈도론자는 추정기 estimator의 파라미터인 w는 변하지 않으며 오차를 데이터 셋의 분포라 보고,

베이지안은 주어진 데이터에 대한 모수의 불확실성을 w에 대한 확률분포로 나타낼수 있다고 한다.

최대 가능도 방법 maximum likelihood method

가장 널리 사용되는 빈도주의적 점 추정 방법으로 최대 가능도 방법이 있는데

가능도 함수 p(D|w)를 최대화 하는 계수벡터 w를 구하는 것이다.

이미 관측된 데이터 셋 D이 있으니 다양한 계수 벡터 w 중에서

최대 가능도 함수 argmax[p(D|w)] = w를 찾게 된다.

ref : throwexception.tistory.com/956

코인던지기로 보는 베이지안과 빈도론자의 차이

베이지안의 장점은 사전확률을 활용한다는 점인데

다음 실험을 통해 살펴보면

3개의 동전을 던지는 실험을 했을때, 세 동전다 앞면이 나왔다.

* D = [1, 1, 1]

이 경우, 빈도주의적 방법인 최대 가능도 추정법을 이용하면 앞으로의 추정확률은 1이 된다.

하지만 실제로는 계속 1이 나올리가 없으며,

베이지안의 관점에서는 기존의 실험에서 계속 1이 나왔으므로(사전 확률),

이후 1이 나올 확률(사후 확률)은 크게 줄어든다.

베이지안 관점의 한계

사전 확률을 믿음도로 구하기 보다는 수학적으로 편한것으로 고르거나

사전 확률을 잘못 구한 경우 좋지 못한 결과를 얻으며

이론 자체는 18세기에 나왔지만 가능한 전체 모수 공간을 주변화해서 다루기는 힘들어

실제 응용할 수가 없었다.

하지만 마르코브 체인 몬테카를로 방법같은 샘플링 방법들이 나오고,

컴퓨터의 계산 속도와 매모리 공간이 커짐에 따라 베이지안 기법이 사용할수 있게 되었음.

가우시안 분포 Guassian distribution

정규 분포라고도 부르며, 정규 분포를 따르는 확률 변수 x에 대한 확률 밀도 함수는

기대값과 2차 모멘트를 이용하여 분산을 구할 수 있음

D 차원 가우시안 분포는 아래와 같이 정리하며

|시그마|는 분산 행렬의 결정식

최대 가능도 법으로 가우시안 분포의 모수 추정하기

다음과 같이 관측 벡터 x가 주어질때

가능도 함수는 아래와 같으며

가능도 함수를 최대화 하는 모수를 찾아야 한다.

최대 가능도 함수를 음의 로그 변환을 수행한 후

각 모수에 대해 미분하여 가장 가능성이 높은 모수들을 구하자

최대 가능도법의 한계

방금 단변수 가우시안 분포에 대해 최대 가능도 법으로 모수를 추정하였지만

이 방법에는 분산을 저평가 한다는 문제점이 있습니다.

추정 평균과 추정 분산의 기대값은 아래와 같은데,

추정 평균의 기대값은 모평균을 동일하지만

추정 분산의 기대값은 (N - 1)/N * 모 분산으로 실제 분산보다 작아지는 현상이 발생합니다. 

위 결과는 표본 분산으로부터 계산해서 얻을 수 있습니다.

* 표본 분산의 기대값은 모분산이므로.

주어진 정규분포로 부터 취득한 3개의 샘플 데이터로 추정한 평균과 분산인데

3가지 결과 다 모분산보다 추정 분산이 작게 나올수 밖에 없습니다.

데이터로 부터 패턴을 찾는 것은 오랫동안 연구되어온 문제인데,

대표적인 예시로 숫자 이미지로부터 이미지에 나온 수가 몇인지 분류하는 것이 있다.

입력 데이터로부터 분류를 하거나 회귀를 하는 패턴 인식 모델은

훈련 데이터 셋과 타겟 벡터로 훈련하여

새로운 입력 데이터를 분류 할 수 있게 된다.

커브 피팅 curve fitting(polynomial regression)을 하는 경우를 예로 들어보자

아래와 같이 입력 벡터 x와 타겟 벡터 t, 다항 계수 벡터 w가 있으며,

y는 입력 벡터 x와 다항 계수 벡터 w의 선형 결합으로 구한다.

이때 M은 다항식의 차수이며, M이 1인경우 선형 모델이라 부른다.

훈련 입력 벡터 x와 훈련 타겟 벡터 t를 이용하여 최적의 다항 계수 벡터를 구하면

새로운 입력 x_hat이 주어질때 이에 대한 예측 결과인 t_hat을 구할 수 있게 된다.

최적의 다항 계수 벡터 w를 구하는 방법은

오차 함수를 활용하면 된다.

오차 함수는 오차(실제 값과 타겟 값의 차이) 제곱 합으로 나타내며

이 오차 제곱합을 최소화 시키는 다항 계수 벡터 w*가 다항 회귀식의 최적 계수가 된다.

다항식의 차수에 따라 다항 회귀식은 다음과 같이 다양한 형태를 띌 수 있다.

차수가 0, 1인 경우 주어진 다항식을 잘 적합하지 못하고 있으나

차수가 3일때는 실제 다항식과 가장 유사한 형태를 띈다.

하지만 차수가 과하게 커진 경우 주어진 데이터에만 맞춰전 과적합 문제가 발생하게 된다.

과적합 over fitting 문제를 피하는 방법으로

규제 적용 regularization 이 있는데

비용함수에 패널티항을 추가하면 된다.

규제항의 람다는 얼마나 다항식 계수 벡터의 노름(벡터의 크기)에 가중치를 줄것인가를 의미하는데

람다가 작으면 제곱합 오차가 크게 반영이되고,

람다가 크다면 제곱합 오차가 상대적으로 적게 반영이 된다.

그런데 패널티가 부여된 비용함수를 최소화 시키는 W*를 찾아야 하므로 

람다가 클 수록 계수 벡터의 가중이 커지니 가능한 작은 W*을 찾고,

람다가 작은 경우 계수 벡터의 가중이 작으니 보다 큰 W*를 찾게 된다.

이 L2 규제의 가중치 값인 람다를 조정함으로서 모델 복잡도에 의한 과적합 문제를 완화 시킬수 있게 된다.

이미지 히스토그램

명암값을 x축, 명암의 빈도수를 y축으로 하는 히스토그램을 말한다

대충 아래와 같이 4 x 4 영상이 주어질때

위 영상의 히스토그램은 아래와 같이 구할수 있다.

정규화 히스토그램 normalized histogram의 경우

모든 픽셀의 명암 값의 합이 1이 되도록 하는 히스토그램으로

위 히스토그램의 값을 전체 크기(y * x) 만큼 나누어 주면 된다.

히스토그램 활용 용도

- 영상 특성 파악

- 평활화로 품질 개선

- 역투영을 통한 얼굴 검출방법

* 색상만을 활용하여 검출하는 방법으로 그다지 좋지 못함.

히스토그램으로 영상 특성 파악하기

첫번째 영상의 경우

밝은 부분과 어두운 부분으로 이분화 할수 있어 히스토그램 상에 봉우리가 2개가 나타남.

두번째 영상은 

시장에서 다양한 밝기 값들이 존재하다보니 고르게 분포된 양상을 보임

마지막 영상은

달 부분이 밝으나 매우 적고, 대부분 어두운 값이 차지하여 50 부근으로 가장 큰 빈도수를 가지고 있음.

import cv2
import matplotlib.pyplot as plt

dark_night = cv2.imread("./res/dark_night.jpg")
market = cv2.imread("./res/conventional_market.jpg")
moon = cv2.imread("./res/moon.jpg")

imgs = [dark_night, market, moon]

figure, axs = plt.subplots(figsize=(16, 16), nrows=3, ncols=3)
width, height = 400, 400

for i in range(3):
    resize = cv2.resize(imgs[i], dsize=(width, height))
    rgb = cv2.cvtColor(resize, cv2.COLOR_BGR2RGB)
    gray = cv2.cvtColor(resize, cv2.COLOR_RGB2GRAY)
    hist = cv2.calcHist(gray,[0],None,[256],[0,256])

    axs[i, 0].imshow(rgb)
    axs[i, 1].imshow(gray, cmap="gray")
    axs[i, 2].plot(hist)

plt.tight_layout()

히스토그램 평활화 histogram equalization를 통한 품질 개선 

위의 첫번째 그림과 같이

히스토그램 상에 명암 값이 한 쪽으로 치우쳐 진 경우

비슷한 명암을 가진 물체끼리 구분하기 어려운데

치우쳐진 명암 분포를 고르게 해주는 방법입니다.

아래와 같이 어두운 영상의 경우

잘 안보이는 부분이 많지만

히스토그램 평활화를 통해 개선 시킬수 있습니다.

위 이미지의 히스토그램을 보면

명암 분포가 낮은 곳 위주로 분포하고 있지만

히스토그램 평활화를 수행하여

명암 분포가 고르게 분포해지면

어두운 영역이 밝아져 선형하게 알아볼수 있게 됩니다.

joker = cv2.imread("./res/joker.jpg")
resize = cv2.resize(joker, dsize=(width, height))
rgb = cv2.cvtColor(resize, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(resize, cv2.COLOR_RGB2GRAY)
hist = cv2.calcHist(gray,[0],None,[256],[0,256])
equ = cv2.equalizeHist(gray)
equ_hist = cv2.calcHist(equ,[0],None,[256],[0,256])



figure, axs = plt.subplots(figsize=(16,16),ncols=2, nrows=2)
axs[0, 0].imshow(gray, cmap="gray")
axs[0, 1].plot(hist)
axs[1, 0].imshow(equ, cmap="gray")
axs[1, 1].plot(equ_hist)
plt.tight_layout()