728x90
선형 판별 분석 LDA : Linear Discriminant Analysis
- PCA와 마찬가지로 차원 축소 기법
- 클래스간 분산을 최대화, 클래스 내부 분산을 최소화 하는 선형 결정식을 찾음

- 클래스 별 중심점과 공분산이 주어질떄 클래스간 분산과 클래스내 분산을 구할수 있음

- 클래스내 분산 행렬과 클래스간 분산 행렬로부터 고유 값과 고유벡터를 추출할수 있음.
- 고유 값은 비중, 고유 벡터는 클래스 내 분산을 최소, 클래스간 분산을 최대로 하는 선형 판별식의 계수

붓꽃 데이터에 선형 판별 분석 적용하기
PCA는 반응 변수가 필요없는 비지도 학습이지만
LDA는 반응 변수 종속 변수가 필요한 지도 학습 알고리즘

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
iris = load_iris()
iris_scaled = StandardScaler().fit_transform(iris.data)
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X=iris.data, y=iris.target)
iris_lda = lda.transform(iris_scaled)
print(iris_lda.shape)
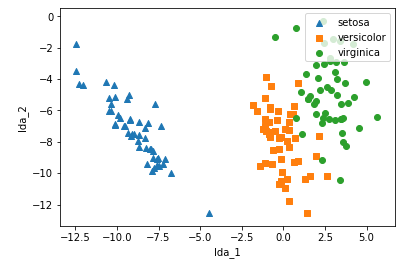
선형 판별 분석을 통해
차원수, 독립변수를 2개로 줄였음에도
클래스 간 분산이 최대, 클래스 내 분산이 최소가 되도록 변환 된 것을 볼수 있음
lda_cols = ["lda_1", "lda_2"]
df = pd.DataFrame(data=iris_lda, columns=lda_cols)
df["target"] = iris.target
markers=["^", "s", "o"]
for i, marker in enumerate(markers):
x_data = df[df["target"]==i]["lda_1"]
y_data = df[df["target"]==i]["lda_2"]
plt.scatter(x_data, y_data, marker=marker, label=iris.target_names[i])
plt.legend(loc="upper right")
plt.xlabel("lda_1")
plt.ylabel("lda_2")
plt.show()
300x250
'인공지능' 카테고리의 다른 글
| 컴퓨터 비전 & 패턴 인식 - 2. 영상 취득과 핀홀 카메라 모델로 보는 카메라 파라미터 (0) | 2020.12.11 |
|---|---|
| 컴퓨터 비전 & 패턴 인식 - 1. 시작 (0) | 2020.12.11 |
| 파이썬머신러닝 - 29. 신용 카드 데이터 분석하기 + PCA (0) | 2020.12.10 |
| 파이썬머신러닝 - 28. 차원 축소와 주성분 분석 (0) | 2020.12.10 |
| 파이썬머신러닝 - 27. 고급 회귀 기법을 이용한 주택 가격 예측 (0) | 2020.12.10 |