집밖은 위험해

그리스어 표기

고유치 eigen value, 고유벡터 eigen vector

- 패턴 인식 + 전기 + 사회 과학 분야 전반에서 사용되는 분석 도구

- 행렬의 중요한 특징을 표현

- 아래의 식을 만족하는 벡터 A가 eigen vector, 스칼라 lambda는 고유치

양의 정부호 행렬

- 0이 아닌 벡터 x와 행렬 A가 다음의 조건을 만족하는 경우

 => 행렬 A는 양의 정부호 행렬 positive definite matrix 

 => A > 0 이 A가 정부호 임을 알려줌

양의 준정부호 행렬

- 0이 아닌 벡터 x와 행렬 A가 다음 조건 만족

 => 행렬 A는 양의 준정부호행렬 positive semi-definite matrix

 => A >= 0. 즉, A는 준정부호

유사 변환 similarity transformation과 고유치

- 유사 변환 =  강체 변환(평행 이동 + 회전) + 스케일 변환

- 다음의 조건을 만족하는 역행렬 C가 존재하면 행렬 A와 B는 유사

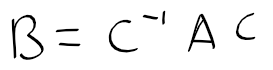
- 유사 변환 행렬들은 동일한 고유치를 가짐

대각화 가능한 행렬 digonalizable

- 아래의 조건을 만족하는 대각행렬 C가 존재할때, 정방 행렬 A는 대각화 가능한 행렬

 * 이후 특이값 분해를 위해 대각화가 가능하여야 함

행렬의 대각화

- 대각 행렬 C가 아래와 같은 열벡터 v들을 모아 만든 행렬이라고 가정할때

- 정방 행렬 A의 고유치, 고유벡터들을  행렬 A와 행렬C의 곱으로 표현 가능

- 행렬 C는 선형 독립 -> 비특이 행렬 => C의 역행렬이 존재한다.

 => 행렬 A는 대각화가 가능함

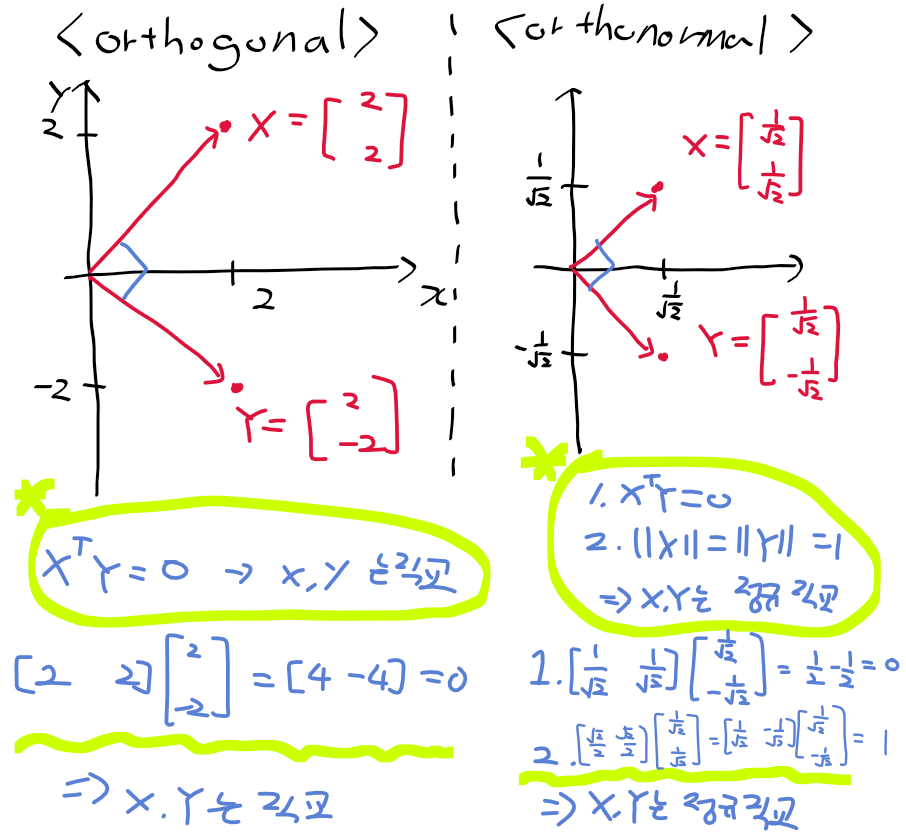
직교 대각화 orthogonal diagonalization

- 직교 행렬의 성질 : 대각 행렬 C가 직교행렬인 경우 C의 전치행렬 = C의 역행렬

- 직교 행렬의 성질을 이용하면 역행렬을 전치행렬로 변환하여 간단하게 계산 가능

특이값 분해 singular value decomposition

- 복습 => 특이 행렬 : 역행렬이 존재하지 않음.   비특이 행렬 : 역행렬이 존재

- 특이 값 분해

 : 특이값 분해(SVD)는 고유값 분해(eigen value decomposition)처럼 행렬을 대각화하는 한 방법

  => 특이 행렬(비정방행렬)에서 특이값(고유값)들에 대한 대각 행렬을 분해한다.

- 특이값 분해의 장점

 :  행렬이 정방행렬이든 아니든 관계없이 모든 m x n 행렬에 대해 적용 가능하기 때문이다.

- 비정방 행렬 A가 주어질때 다음의 관계가 이루어짐.

고유값 분해 eigen value decomposition과 특이값 분해 Singular Value Decomposition의 차이

- 고유값 분해는 정방행렬 A의 고유값들을 대각행렬로 추출

- 특이값 분해는 비정방행렬들의 특이값(행렬의 특성을 가장 잘나내는 값)을 대각행렬로 추출

선형 변환 linear transform

- 아래와 같이 서로 다른 차원의 벡터 공간에서 변환(맵핑)을 의미

- 아래의 예시는 2차원 벡터공간 X에서 3차원 벡터공간 Y로의 선형 변환을 보여줌

- 선형 변환을 행렬로 표기하면 아래와 같다.

행렬의 트레이스 trace

- 정방 행렬의 대각 성분들의 합 => 트레이스

행렬의 계수 rank

- 선형 독립인 열벡터(행벡터)의 갯수

- 3 x 3행렬이라고 항상 계수가 3은 아님

 => 크기가 n x n이더라도 선형 독립인 행벡터가 1개 뿐이면, rank(A) = 1

- 행렬의 랭크는 다음의 조건을 따른다.

특이 행렬과 비특이 행렬

- 크기가 n x n 인 행렬 A가 주어질때 rank(A) = n이면 비특이 행렬, rank(A) < n이면 특이행렬

역행렬 inverse matrix

- 행렬 A가 주어질때, A와 곱했을때 단위 행렬 I가 나오는 행렬.

- ex. AB = I => A의 역행렬은 B

수치 해석적으로 역행렬을 구하는 방법

- 소행렬식 전개

- 가우스 조던 소거법

행렬식 determinant of matrix

- 행렬을 하나의 실수 값으로 표현하는 식

+ 역행렬이 존재하는지를 판별하기 위한 식

- 행렬 A의 행렬식은 아래와 같이 표기

- 크기가 2 x 2인 경우, 3 x 3인 경우 행렬식 계산법( 사루스 전개법으로 쉽게 계산 가능)

* 4차 이상 행렬의 경우 소행렬식 사용하여 계산 가능

잠깐

- 벡터 공간 : n차원 벡터들이 존재하는 n차원 공간

- 유클리드 공간 : 선형독립인 n개의 n차원 벡터로 생성될수 있는 공간

- 함수 공간 : 벡터 차원이 무한대인경우

- 널 공간 : 행렬 A가 주어질떄 Ax = 0을 만족하는 벡터 x들로 이루어진 공간

행렬론

- 행렬 : 행 M개와 열 N개로 이루어진 수들의 나열

- 차원 : M x N으로 행렬의 크기

행렬의 종류

- 전치행렬 tranposed matrix : 행과 열을 바꾼 행렬

- 정방행렬 square matrix : 행과 열의 크기가 동일한 행렬

- 대각 행렬 diagonal matrix : 대각 요소만 존재하는 행렬

- 상삼각 행렬 upper triangular matrix : 대각 성분 아래가 모두 0인행렬

- 하삼각 행렬 lower triangular matrix : 대각 성분 위가 모두 0인행렬

- 항등 행렬 identity Matrix : IA = AI = A를 만족하는 행렬 I

- 대칭 행렬 symmetric matrix : 대각선을 축으로 모든 선분이 대칭인 행렬. 전치를해도 자기자신인 정방행렬

- 영행렬 zero matrix : 모든 원소가 0 인 행렬

직교 행렬 orthogonal matrix

- 행렬 A가 아래의 조건을 만족하는 행렬

=> 다변량 통계 분석에서 요인 분석 factor analysis나 주성분 분석 principal component analysis, 판별 분석 discriminant analysis 에서 많이 사용되는 행렬

정규 직교 행렬 orthonomal matrix

- 행렬 A가 직교 행렬이며 다음의 조건을 만족하는 경우 정규 직교 행렬임

벡터 vector

- 크기와 방향을 가지는 물리량

특징 벡터 feature vector

- 차원을 가지는 벡터

벡터의 전치 transeposed vector

- 벡터의 원소를 행과 열을 바꾼것

벡터의 크기, 노름 norm

- 원점에서 벡터공간상 한점까지의 거리

단위 벡터 unit vector

- 특정 방향에 대해 길이가 1인 벡터

벡터의 연산

1. 스칼라 곱

- 벡터에 스칼라(실수) 곱하는 연산

2. 내적 dot product

- 점으로 표기하기 때문에 점곰, 혹은 결과가 스칼라이므로 스칼라 곱, 꺽쇄를 사여 표기하기도 함.

3. 외적 cross product

- 벡터끼리 곱하여 벡터가 나와 벡터 곱, 교곱이라고도 부르는 연산

- 자세한 연산은 공업수학 참조

수직 사영 projection

- 벡터 y를 벡터 x에 사영하면, x방향의 벡터가 생김

벡터의 직교(수직)과 정규 직교

- 아래의 조건을 만족하는 경우 두 벡터 x, y는 수직 orthogonal/정규 직교 orthonormal이됨.

선형 결합 linear combination

- 벡터 집합과 스칼라 계수 집합들의 곱, 합이 선형성을 가지고 있으면 선형 결합. 1차결합이라고 부름

선형 독립과 선형 종속

- 아래의 벡터 집합과 스칼라 계수 집합이 주어질때

- 선형 독립 : 모든 a_i = 0인 경우에만 성립하는 경우. 벡터 집합은 선형 독립 linear indepent

- 선형 종속 : 선형 독립이 아닌 경우. 선형 종속 linear dependent

기저 

- 스칼라 곱을 해서 벡터 공간을 생성할수 있는 벡터

- ex

  기저 벡터 : (1, 0)가 주어질때

   a (1, 0) => (2, 0), (3, 0), (4, 0) 등의 생성 벡터 공간(span vector space)이 만들어짐

기저 집합

- 2차원에서의 기저 (1, 0), (0, 1)

- 3차원에서 기저 (1, 0, 0), (0, 1, 0), (0, 0, 1) 과 같이

 벡터 공간을 생성해내는 기저의 모임

그램 슈미트 직교화 과정

- n개의 선형 독립 벡터가 주어질때, 생성 벡터공간에 대한 정규 직교 기저를 찾을 수 있음

- 아래의 경우 3개의 선형 독립 벡터(u1, u2, u3)가 주어질때 생성 벡터(v1, v2, v3) 공간을 보여줌