Building Blocks of a Deep Neural Network (C1W4L05)

순전파와 역전파 함수

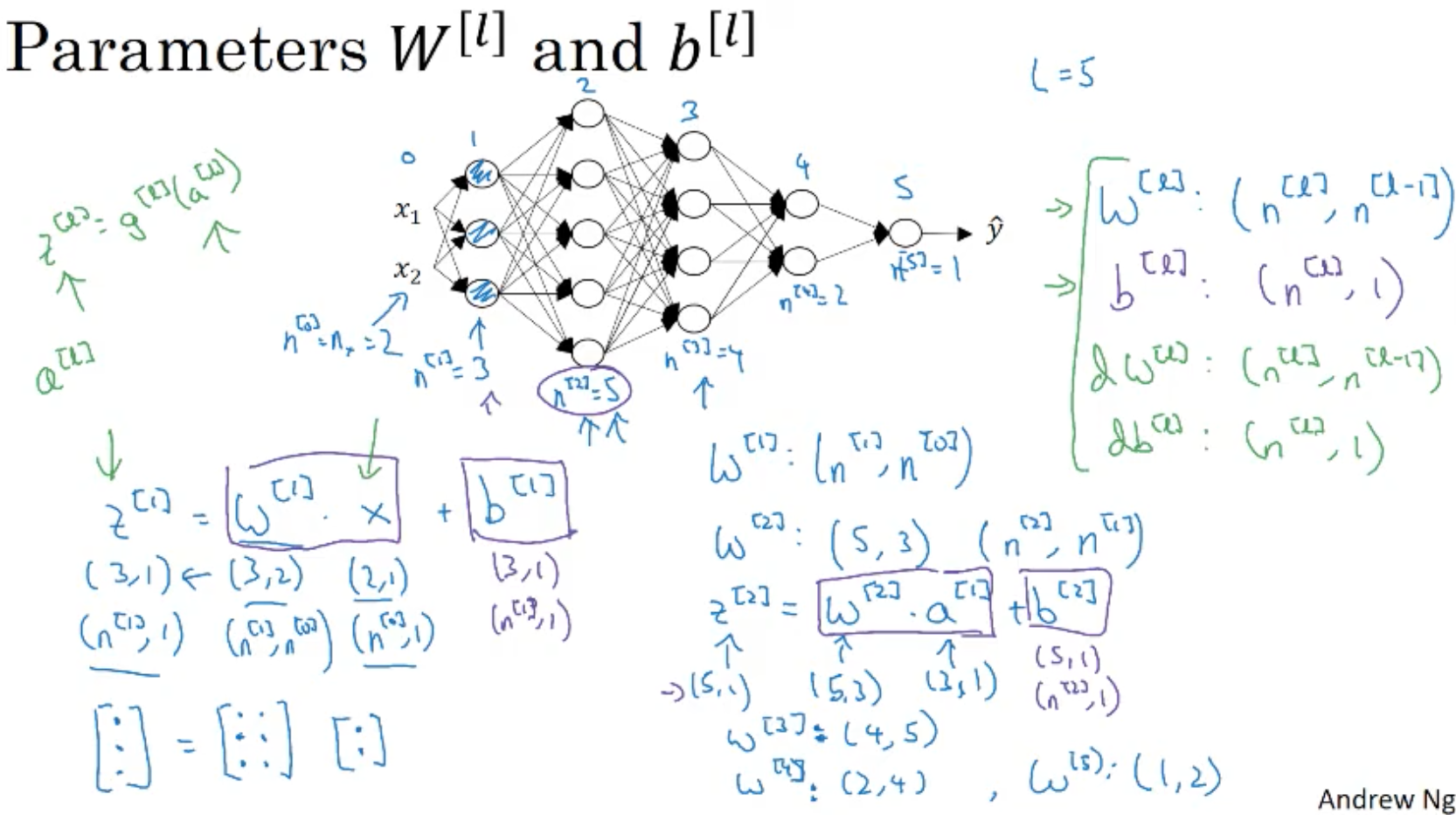
- l layer를 중심으로 살펴보자. w^[l], b^[l]

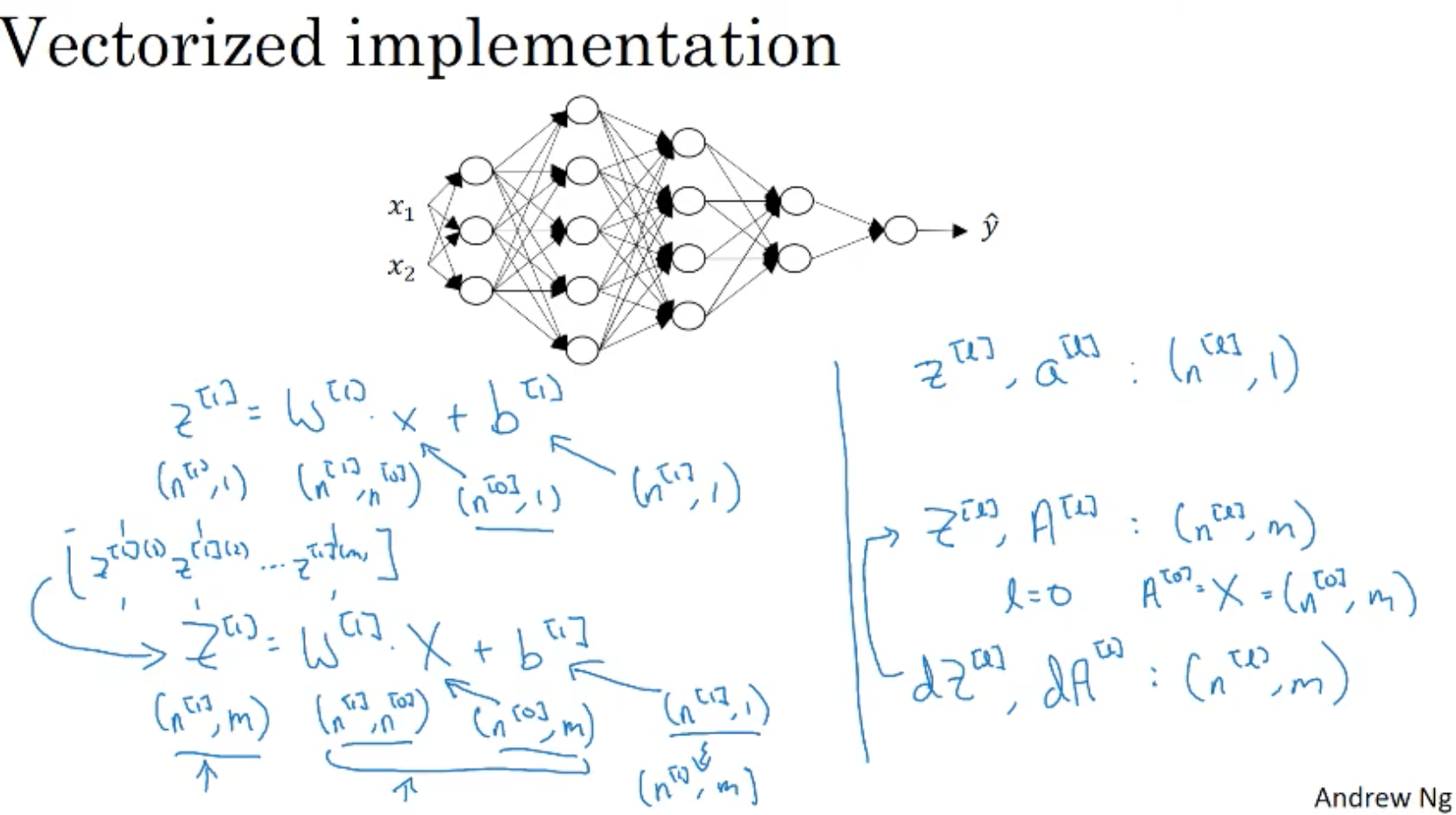
- 순전파 : 입력 a^[l-1], 출력 a^[l], z^[l] = w^[l] a^[l-1] + b^[l], a^[l] = g^[l](z^[l]).

  * z^[l]은 캐싱한다.(역전파때 사용하게 임시 저장함.)

- 역전파 : input da^[l], cache z^[l],   -> output : da^[l-1], dw^[l], db^[l]

=> 역전파 계산시 이전 레이어 da^[l]와 순전파때 캐싱한 z^[l]로 w,b, a에 대한 그라디언트들을 계산한다.

- 입력부터 출력까지 순전파, 역전파 연산 과정을 블록으로 보자.

* da^[0]의 경우 w나 b의 그라디언트, 미분계수를 계산하는데 필요없음.

* 그라디언트 계산에 w, b 도 필요하므로 같이 캐싱하자.

Why Deep Representations? (C1W4L04)

- 왜 심층 신경망이 잘 동작하는지 알아보자

심층 표현을 이해하기

- 얼굴 인식, 감지 시스템 구축 시 심층 신경망이 할수 있는 일을 알아보자

- 첫번째 레이어는 특징/에지 검출기 역활을 함. 아래의 그림에서 20개의 은닉층을 시각화 한 결과들을 보여주고 있다.

- 검출된 에지들을 모아 얼굴의 일부분을 찾아낼수/감지해낼 수 있다.

- 서로 다른 얼굴 일부분들을 모아 다양한 얼굴들을 구분할 수 있게 됨.

- 스피치 인식 시스템을 만든다고 해보자

- 신경망의 첫번째 레이어에서는 오디오의 저수준 특징들을 찾아낼 것임.

- 이러한 저수진 특징들을 모아 기본 소리 단위들을 만들어냄 -> 단어들을 인식하고 -> 문장을 인지하게 됨.

- 깊어질수록 단순한 표현에서 더욱 복잡한 표현들로 섞이게 됨.

* 사람의 뇌도 에지 단위부터 인식해서 사람의 얼굴을 구분할 수 있음.

회로이론과 딥러닝

- 왜 심층 신경망이 잘 동작하는가에 대해서 회로 이론에서 나옴.

- 회로 이론에서는 서로 다른 회로들을 조합해서 어떤 함수 역활을 수행함.

- L 레이어 작지만(은닉 유닛이 적다) 깊은 심층 신경망에 대한 함수를 얕은 신경망으로 계산하고자 한다면 지수적으로 훨씬 많은 은닉 유닛들이 필요로함.

- 모든 입력에 대한 베타적 논리합을 구하는 함수 구현시, 심층으로 구현한다면 O(log n) 복잡도를 가지나, 심층으로 구현하지 못하고 얕게 구현한다면 모든 경우의 수를 나열해야해서 은닉층이 지수적으로 증가함.

=> 회로 이론을 통해서도 깊게 쌓을수록 더 계산하기 쉽다.

Getting Matrix Dimensions Right (C1W4L03)

파라미터 w와 b

- 심층 신경망 구현시 행렬 차원을 잘 확인 해야 한다. 직접 적어가면서 확인해 보자

- L = 5

- z^1 = w^1 x + b^1

- n^[0] = 2, n^[1] = 3, n^[2] = 5, n^[3] = 4, n^[4] = 2, n^[5] = 1

- z^1's shape = (3, 1) = (n^[1], 1)

- x's shape = (2, 1) = (n^[0], 1)

 => w^1's shape = (3, 2) = (n^[1], n^[0])

 => w^l's shape = (n^[l], n^[l-1]) 

- w^3's shape = (4, 5) = (n^[3], n^[2])

- bias

 b^[1]'s shape = (3, 1) = z^[1]

 b^[l]'s shape = z^[l]

벡터화 구현

- w, dw, b, db의 차원은 동일하나 x와 z, a는 변함.

- 단일 샘플에서 z^[l], a^[l] : (n^[l], 1)

- 전체 셋에선 Z^[l], A[l] : (n^[l], m)

- 입력 X = (n^[0], m)

- 심층 신경망 구현시 차원 부분을 놓치다가 버그 발생할 수 있으니 조심하자.

Forward Propagation in a Deep Network (C1W4L02)

심층 신경망에서 순전파 연산

- 첫번째 레이어 연산 

  z1 = w1x + b1

  a1 = g1(z1) = g1(w1x.+ b1)

- 두번째 레이어의 연산

  z2 = w2a1 + b2

  a2 = g2(z2)

- 위는 단일 훈련 샘플에 대한 연산 과정, 전체 훈련 샘플(데이터셋)에 대해 벡터화는 어떻게 구현될까

 Z1 = w1X + b1

 A1 = g1(Z1)

 Z2 = w2A1 + b1

 A2 = g2(Z2)

 ...

- 가능한 반복문을 사용하지 않는것이 좋으나 각각 훈련 샘플에 대해서는 벡터화가 가능하나 각 계층별로는 반복문으로 연산할 수 밖에 없음.

Deep L-Layer Neural Network (C1W4L01)

심층 신경망이란 무엇일까?

- 아래의 그림에는 로지스틱회귀, 은닉층이 1개(2층), 2개(3층), 5개(6층)인 신경망

- 로지스틱 회귀 모델은 얕은 모델(1층 신경망)이지만, 6층 신경망은 비교적 깊다.

심층 신경망 표기법

- 아래의 그림은 4층 신경망

- L = 4, n^[l] = 해당 레이어의 유닛개수 (ex : n^[0] = n_x = 3, n^[1] = 5, n^[3] = 3)

- a^[l] = 해당 레이어의 활성 결과

Gradient Descent For Neural Networks (C1W3L09)

- 경사 하강을 동작시키는데 필요한 식에 대해서 알아보자.

신경망에서의 경사 하강법

- 파라미터로 각 층의 가중치 행렬과 편향이 있다. w1, b1, w2, b2

- 입력 n0, 은닉층 n1, 출력 n2(하나의 출력값)

- 비용함수 (이진 분류를 하는 경우로 고려) : J(w1, b1, w2, b2) = 1/m L(예측치, 실제치)

 * 손실함수는 하나의 샘플에 대한 예측과 실제치의 차이 평가

- 경사 하강하기

  1. 예측치 계산

  2. 그라디언트 계산

    dw1 = dJ/dw1,    db1 = dJ/db1,  . . . .

  3. 학습 파라미터 갱신 

    w1 = w1 - alpha * dw1 . . .

  4. 반복

미분계수 계산 공식

- 우선 순전파 계산 공식

  A1 = g1(z1) = g1(w1x1 + b1)

  A2 = g2(w2A1 + b2)

- 미분 계수 계산, 역전파 단계

  아래의 그림 참조

Explanation For Vectorized Implementation (C1W3L05)

벡터화 구현 정리하기

- 1, 2, 3번째 샘플들에 대한 첫번째 레이어의 활성 결과들을 구해보자.

- 첫번째 레이어의 편향들은 정리를 위해서 깔끔하게 하기위해서 0으로.

- 첫번째 레이어의 가중치 행렬과 평행하게 쌓은 샘플 데이터의 행렬 곱 연산으로 한번에 Z를 구할 수 있다.

여러 훈련 샘플을 이용한 벡터화 연산 정리

- 벡터화를 통해서 좌측 상단의 반복문을, 행렬곱 연산으로 바꾸어 빠르게 처리가 가능해짐.